符号动力系统的弱混合子集和传递子集

刘 磊, 彭冬梅(. 商丘师范学院 数学与信息科学学院, 河南 商丘 476000; . 郑州大学 数学与统计学院, 河南 郑州 45000)



符号动力系统的弱混合子集和传递子集

刘 磊1, 彭冬梅2
(1. 商丘师范学院 数学与信息科学学院, 河南 商丘 476000; 2. 郑州大学 数学与统计学院, 河南 郑州 450001)

研究了符号动力系统的弱混合子集和传递子集的性质，讨论了符号动力系统中弱混合子集与传递子集之间的关系，给出了符号动力系统的传递子集是弱混合子集的一个充分条件.

符号动力系统； 弱混合子集； 传递子集

拓扑传递，弱混合是描述拓扑动力系统全局特征的概念.设(X,f)为拓扑动力系统.(X,f)是拓扑传递的，如果对X中的任意非空开子集U和V，则存在n∈N使得fn(U)∩V≠Ø；(X,f)是弱混合的，如果对X中的任意非空开子集U1,U2,V1和V2，则存在n∈N使得fn(U1)∩V1≠Ø，fn(U2)∩V2≠Ø.由上面定义知，弱混合蕴含拓扑传递.

文献[1]介绍了整体性质和部分性质.例如，敏感初值依赖，Devaney混沌，弱混合属于整体性质;Li-Yorke混沌和正拓扑熵属于部分性质.文献[2]给出了弱混合子集的定义,并且证明了“含有弱混合子集的动力系统是Li-Yorke混沌的”.后来,文献[3]推广了弱混合子集的定义并且给出了传递子集的定义以及讨论了它们的基本性质.自此,弱混合子集和传递子集的研究就成为拓扑动力系统的一个研究热点.P. Oprocha等[4]进一步讨论了传递子集和弱混合子集的拓扑结构问题;接着,P. Oprocha等[5]研究了弱混合子集与序列熵以及混沌之间的关系.文献[6-8]讨论了弱混合子集的性质以及非自治离散动力系统的传递子集和弱混合子集的问题.最近,文献[9]研究了弱混合子集与Furstenberg族之间的关系.

本文将讨论符号动力系统的弱混合子集和传递子集之间的关系，证明了如果符号动力系统的传递子集是一个正则闭集，那么这个传递子集是符号动力系统的弱混合子集.

1 基本理论

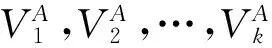
显然，由定义1.1，如果(X,f)是弱混合的，则X是(X,f)的一个弱混合子集.

定义 1.2[3]设(X,f)为拓扑动力系统，A为X的非空子集.A称为(X,f)的传递子集，如果对A的任意非空开子集VA，X的开子集U且A∩U≠Ø，那么存在n∈N使得fn(VA)∩U≠Ø.

显然，如果A为(X,f)的弱混合子集，则A为(X,f)的传递子集.

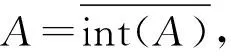
据定义1.3，A是X的正则闭集当且仅当对A的任意非空集VA，有int(VA)≠Ø.

设整数p≥2，任取p个不同符号0,1,…,p-1.记S={0,1,…,p-1}，赋S以“离散拓扑”，即S的每一个元素都是开集因而也就是闭集.显然S是一个紧致拓扑空间.

作拓扑积

{x=(x0,x1,x2,…)|xn∈S,∀n≥0}.

由文献[11]知，SZ+是紧致空间.

设ai∈S，i=0,1,…,n-1，n∈N.又设m∈Z+.记

m[a0,a1,…,an-1]=

{x∈Σk|xm+i=ai,i=0,1,…,n-1}.

据文献[12-15]，m[a0,a1,…,an-1]叫作S上有限序列(a0,a1,…,an-1)上的柱形.易于看出，柱形既是开集，又是闭集，并且全体柱形的集合是可数的，而且构成了Σk的乘积拓扑的一组基.

在Σp上定义转移自映射

σ:Σp→Σp,σ(x0,x1,…)=(x1,x2,…),

则σ是连续的.(Σp,σ)称为符号动力系统.

2 主要结果

命题 2.1 符号动力系统(Σp,σ)存在传递子集.

证明 记A=0[a0,a1,…,am-1].下面证明柱形A为(Σp,σ)的一个传递子集.设VA为A的任意非空开子集，U为Σp的任意开子集，并且U∩A≠Ø.因为VA为A的开子集，所以存在Σp的开子集V，使得VA=V∩A.又由于A为Σp的既开又闭的子集，所以VA也是Σk的开子集.进而，存在柱形B，使得B⊆VA.从A的构造知，存在q∈N且q>m，使得B=0[a0,a1,…,aq].因为σq+1(B)=σq+1(0[a0,a1,…,aq])=Σp，所以σq+1(VA)=Σp.进而，σq+1(VA)∩U=Σp∩U=U≠Ø.这说明了A是(Σp,σ)的一个传递子集.因此，(Σp,σ)存在传递子集.

命题 2.2 符号动力系统(Σp,σ)存在弱混合子集.

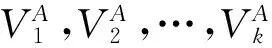
下面给出符号动力系统的传递子集是弱混合子集的一个充分条件.

定理 2.1 设A为Σp的正则闭集且不是单点集.如果A是(Σp,σ)的传递子集，则A是(Σp,σ)的弱混合子集.

例 2.1 设(Σ2,σ)为符号动力系统，则柱形0[0,1]是(Σ2,σ)的一个弱混合子集.

设A=0[0,1]，因为A是一个柱形，所以A是Σ2中开集也是闭集.进而，A是Σ2的正则闭集.由定理2.1，只需证明A是(Σ2,σ)的传递子集.设VA是A的任意非空开子集，U是Σ2的非空开子集并且U∩A≠Ø.不妨设VA=0[0,1,a2,…,aN-1]，从而当m≥N时，σm(VA)=Σ2.因此，σm(VA)∩U=Σ2∩U=U≠Ø.这说明了A是(Σ2,σ)的一个传递子集.

[1] Blanchard F. Topological chaos:what may this mean[J]. J Difference Equ Appl,2009,15:23-46.

[2] Blanchard F, Huang W. Entropy sets, weakly mixing sets and entropy capacity[J]. Discrete Cont Dynam Sys,2008,20:275-311.

[3] Oprocha P, Zhang G. On local aspects of topological weak mixing in dimension one and beyond[J]. Stud Math,2011,202:261-288.

[4] Oprocha P, Zhang G. On sets with recurrence properties, their topological structure and entropy[J]. Top Appl,2012,159:803-811.

[5] Oprocha P, Zhang G. On local aspects of topological weak mixing, sequence entropy and chaos[J]. Ergo Theo Dynam Syst,2014,34:1615-1639.

[6] Liu L. Uniform convergence and transitive subsets[J]. Discrete Dynamics in Nature and Society,2012,2012:970934.

[7] 刘磊. 弱混合子集的等价定义及其应用[J]. 四川师范大学学报:自然科学版,2013,36(3):393-395.

[8] Liu L, Sun Y. Weakly mixing sets and transitive sets for non-autonomous discrete systems[J]. Adv Difference Eqns,2014,2014:217.

[9] Li J. Localization of mixing property via Furstenberg families[J]. Discrete Cont Dynam Sys,2015,35:725-740.

[10] Dickman Jr R F. Regular closed maps[J]. Proc Amer Math Soc,1973,39:414-416.

[11] Engelking R. General Topology[M]. Warszawa:PWN,1977.

[12] Robinson C. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos[M]. 2nd ed. Boca Raton:CRC Press Inc,1999.

[13] 周作领. 符号动力系统[M]. 上海:上海科技教育出版社,1997.

[14] 叶向东,黄文,邵松. 拓扑动力系统概论[M]. 北京:科学出版社,2008.

[15] 周作领,尹建东,许绍元. 拓扑动力系统:从拓扑方法到遍历理论方法[M]. 北京:科学出版社,2011.

2010 MSC：54H20; 28D20

(编辑 周 俊)

On Weakly Mixing Subsets and Transitive Subsets in Symbolic Dynamics

LIU Lei1, PENG Dongmei2
(1.SchoolofMathematicsandInformationScience,ShangqiuNormalCollege,Shangqiu476000,Henan;2.SchoolofMathematicsandStatistics,ZhengzhouUniversity,Zhengzhou450001,Henan)

In this paper we study the properties of transitive subsets and weakly mixing subsets of symbolic dynamics, and we discuss the relation between weakly mixing subsets and transitive subsets in symbolic dynamics and give a sufficient condition that a transitive subset of symbolic dynamics is a weakly mixing subset.

symbolic dynamics; weakly mixing subset; transitive subset

2015-01-14

国家自然科学基金青年基金(11401363)和河南省教育厅项目(14B110006)

刘 磊(1981—)男，讲师，主要从事微分方程与动力系统的研究,E-mail:mathliulei@163.com

O189.11

A

1001-8395(2015)06-0843-03

10.3969/j.issn.1001-8395.2015.06.010