分裂的Euler-Maruyama误差修正法
2015-05-04殷政伟王天军河南科技大学数学与统计学院河南洛阳471003
殷政伟, 王天军(河南科技大学 数学与统计学院, 河南 洛阳 471003)
分裂的Euler-Maruyama误差修正法
殷政伟, 王天军
(河南科技大学 数学与统计学院, 河南 洛阳 471003)
在Euler-Maruyama方法基础上提出一种新的显式的分裂法,该方法可以用来求解随机常微分方程的数值解.与Euler-Maruyama方法相比,该方法具有较大的均方稳定域,因此该方法可以用来求解一些刚性随机微分方程.最后,通过数值算例说明该方法的有效性及可实现性.
随机微分方程数值解; 误差修正法; 分裂法; Euler-Maruyama方法
随机微分方程由于考虑了随机噪声对系统变化的影响,因此,较确定性微分方程更能准确地刻画、描述现实生活中的各种现象.随机微分方程模型在众多应用领域,如生物、化学、微电子学、经济、金融等领域都有广泛的应用[1-5].1951年,日本数学家K. It发表了划时代的著作[6],给出了随机微分方程(SDE)的严格数学描述,建立了随机积分,创立了随机微分方程理论.此后,随机微分方程理论得到快速发展.然而对于随机微分方程而言,它的解析解是非常少见的,因此对于它的数值解的研究具有非常重要的现实意义和应用价值.
随机微分方程的数值方法[7]主要分为2大类,一类是显式方法,例如经典的Euler-Maruyama方法[8]、Milstein方法[9]和Runge-Kutta方法[10].显式方法的特点是计算量较小,计算方便,容易实现,只要给定初值后便可以直接计算.但显式方法的稳定性较差,在遇到刚性问题时,对步长的要求极为严格.相比较而言,隐式方法具有较好的稳定性,如平衡法[11]、强1阶平衡Milstein方法[12]、分步平衡Milstein方法[13]、隐式Taylor方法[14]、全隐的1阶和1.5阶的Runge-Kutta型方法[15]等.隐式方法虽然在求解刚性随机微分方程时有着较好的稳定性,但是由于是隐格式,每一步计算时都要求解一个大型的非线性方程组,这对于一些较复杂的问题,计算量无疑要增加很多,甚至不一定能够实现,因此构造一些具有较好稳定性的显式数值方法就显得尤为重要.在这方面,近年来,也有一些成果,可参考文献[16-17].
本文主要研究自治的随机微分方程,其形式为
(1)
其中,T是一个正常数,f:Rd→Rd是漂移项系数,g=(g1,g2,…,gm):Rd→Rd×m是扩散项系数.w(t)是定义在完备概率空间(Ω,F,{Ft}t≥0,P)上的一个m维的维纳过程,概率空间的滤子{Ft}t≥0满足通常的条件,即{Ft}t≥0是递增右连续的,且F0包含所有的零测集.初值x0与维纳过程w(t)是相互独立的,且满足E|X0|2<∞.
受到文献[18]构造求解常微分方程的误差校正法思想的启发,提出一种分裂的Euler-Maruyama误差修正法,该方法是一个显式方法,但却有较好的稳定性.
1 Euler误差修正法
Euler误差修正法是求解常微分方程初值问题
(2)
的一种显式方法,收敛阶较高,且稳定域较大,所以可以用来求解刚性微分方程.Euler误差修正法的原理是利用切比雪夫配点法求解Euler多项式与常微分方程初值问题(2)的准确解的差所满足的微分方程,然后将所求得的解,即修正项加到Euler法上即可.下面简要介绍Euler误差修正法的推导过程.
在区间[tn,tn+1]上,设y(t)为Euler多项式
y(t)=yn+(t-tn)f(tn,yn).
(3)
定义φ(t)为方程(2)的准确解x(t)与Euler多项式y(t)的差,即
φ(t)=x(t)-y(t),
则φ(t)满足如下的线性微分方程
φ′(t)=G(t)φ(t)+F(t),
t∈[tn,tn+1],
(4)

F(ts)),s∈[-1,1],
(5)

ξ.
令C=max|f″xx(t,χ)|,可以得出
).
因此(5)式可以转化为
sj=cosm-jmπ,j=0,1,…,m

(7)
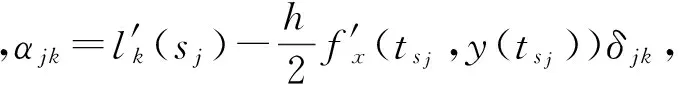
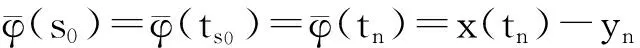
d=[β1,β2,…,βm]T,
F=[F(ts1),F(ts2),…,F(tsm)]T,

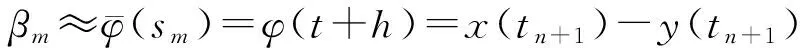
yn+1=yn+hf(tn,yn)+βm.
(8)
2 分裂的Euler-Maruyama误差修正法及其稳定性
将第一节中所提到的Euler误差修正法稍做变动应用到随机微分方程(1),得出分裂的Euler-Maruyama误差修正法.在离散的小区间[tn,tn+1]上,该方法的形式如下
(9)
其中,yn是方程(1)的解析解x(t)在tn时刻的近似值,h是步长,βm是Euler法求解常微分方程初值问题时误差的修正项.
同常微分方程一样,随机微分方程数值解法的稳定性也是通过一线性测试方程进行分析.考虑如下形式的线性标量测试方程
(10)
其中λ,μ∈R是常数,x0依概率1不等于零,方程(10)的准确解为
).
用单步方法求解测试方程(10)得到随机差分方程
(11)

定义 1 对于固定的λ,μ,h,一种数值方法称为均方稳定的,如果

引理 1[18]将方法(8)应用到Dahlquist测试方程x′(t)=λx(t)可以得到差分方程
yn+1=Sm(p)yn,n≥0,
p=λh,其中稳定函数Sm(p)可以表示为
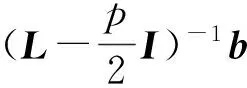
注 1 当m=1,2,3,4时,稳定函数Sm(p)可分别表示为
定理 1 对于固定的λ、μ、h,分裂的Euler-Maruyama误差修正法是均方稳定的,如果有
Sm(p)+q2<1,
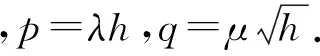
证明 由引理1可知,将分裂的Euler-Maruyama误差修正法应用到测试方程(10)可得
yn+1=Sm(p)yn+μyn△wn,
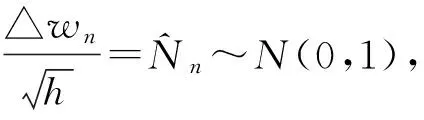
为了更直观的看到分裂的Euler-Maruyama误差修正法的均方稳定域,利用Matlab软件分别画出2种方法的均方稳定域.图1中圆内部是Euler-Maruyama方法的均方稳定区域,另一条曲线内部是m=2时分裂的Euler-Maruyama误差修正法的均方稳定区域,其中.从图1中可以明显看出,经过误差修正后的分裂Euler-Maruyama方法的均方稳定区域比Euler-Maruyama方法的均方稳定域增大了很多.

3 数值实验
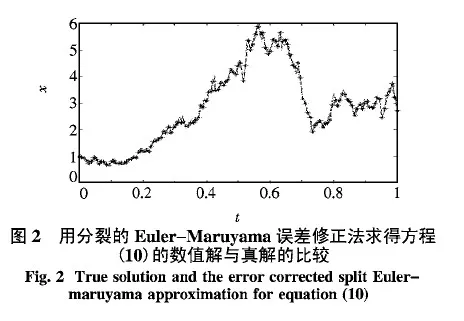
取m=2,用分裂的Euler-Maruyama误差修正法求解测试方程(10),其中λ=2,μ=1,x0=1.图2中曲线是测试方程(10)的精确解,带*曲线是用分裂的Euler-Maruyama误差修正法求得的数值解,从图2可以看出,数值解与真解吻合得很好.
4 结语
本文在切比雪夫配点法的基础上,提出一种新的求解随机常微分方程数值解的显式方法.该方法在求解随机常微分方程时,算法简单,计算量小,且与同阶的Euler-Maruyama方法相比,该方法的均方稳定域增大很多,因此也可以考虑用该方法求解一些具有刚性的随机常微分方程.
[1] Oksendal B. Stochastic Differential Equations:an Introduction with Applications[M]. 5th ed. Berlin:Springer-Verlag,1998.
[2] Mao X. Stochastic Differential Equations and Applications[M]. Chichester:Horwood,1997.
[3] Sobczyk K. Stochastic Differential Equations with Application to Physics and Engineering[M]. Dordrecht:Kluwer Academic,1991.
[4] Hobson D, Rogers L. Complete models with stochastic volatility[J]. Math Finance,1998,8:27-48.
[5] 杨鹏. 基于确定缴费型养老金最优投资的随机微分博弈[J]. 四川师范大学学报:自然科学版,2015,38(2):194-200.
[7] Kloeden P E, Platen E. Numerical Solution of Stochastic Differential Equations[M]. Berlin:Springer-Verlag,1992.
[8] Maruyama G. Continuous Markov processes and stochastic equations[J]. Rend Circ Mat Palermo,1955,4:48-90.
[9] Milstein G N. Approximate integration of stochastic differential equations[J]. Theory Prob Appl,1974,19(3):557-562.
[10] Rumelin W. Numerical treatment of stochastic differential equations[J]. SIAM J Numer Anal,1982,19(3):604-613.
[11] Milstein G N, Platen E, Schurz H. Balanced implicit methods for stiff stochastic systems[J]. SIAM J Numer Anal,1998,35(3):1010-1019.
[12] Kahl C, Schurz H. Balanced Milstein methods for ordinary SDEs[J]. Monte Carlo Meth Appl,2006,12(2):143-170.
[13] Wang P, Liu Z. Split-step backward balanced Milstein methods for stiff stochastic systems[J]. Appl Numer Math,2009,59:1198-1213.
[14] Tian T, Burrage K. Implicit Taylor methods for stiff stochastic differential equations[J]. Appl Numer Math,2001,38:167-185.
[15] Burrage K, Tian T. Implicit stochastic Runge-Kutta methods for stochastic differential equations[J]. Bit Numerical Math,2004,44:21-39.
[16] Abdulle A, Cirilli S. Stabilized methods for stiff stochastic systems[J]. C R Acad Sci,2007,345(10):593-598.
[17] Abdulle A, Cirilli S. S-ROCK methods for stiff stochastic problems[J]. SIAM J Sci Comput,2008,30(2):997-1014.
[18] Kim P, Piao X, Kim S D. An error corrected Euler method for solving stiff problems based on Chebyshev collocation[J]. SIAM J Numer Anal,2011,49(6):2211-2230.
2010 MSC:34A05; 65L05
(编辑 郑月蓉)
An Error Corrected Split Euler-Maruyama Method
YIN Zhengwei, WANG Tianjun
(SchoolofMathematicsandStatistics,HenanUniversityofScienceandTechnology,Luoyang471003,Henan)
In this paper, a new explicit split method is proposed based on Euler-Maruyama method. This method can be applied to solve the stochastic differential equations. Compared to Euler-Maruyama method, this method has larger mean-square stability region. Therefore, the method can be used to solve stiff stochastic differential equations. Some numerical experiments illustrate the effectiveness and operability.
numerical solution of stochastic differential equations; error corrected method; split method; Euler-Maruyama method
2014-07-08
国家自然科学基金(11371123)和教育部博士点基金(20120162120096)
殷政伟(1980—),女,博士生,主要从事随机微分方程数值解的研究,E-mail:yzw_0379@163.com
O241.8
A
1001-8395(2015)06-0830-04
10.3969/j.issn.1001-8395.2015.06.007
