Hilbert空间中变分不等式的一种新算法

方长杰, 王 盈(重庆邮电大学 理学院, 重庆 400065)



Hilbert空间中变分不等式的一种新算法

方长杰, 王 盈
(重庆邮电大学 理学院, 重庆 400065)

提出在Hilbert空间中求解变分不等式问题的新的混合超梯度算法,在f是单调且连续的映射的假设下,证明由新的混合超梯度算法所生成迭代序列强收敛到变分不等式问题的解集与可数无限个非扩张映射的不动点集合的公共元素.

变分不等式; 不动点; 非扩张映射; 连续映射; 单调映射; 强收敛

变分不等式问题(简记VI(f,K)):设K为实Hilbert空间上的一个非空闭凸集,f:K→K是一个连续映射.求x*∈K,使得

〈f(x*),x-x*〉≥0, ∀x∈K.

(1)

本文中,K*表示VI(f,K)的解集并且假设它是非空的.

变分不等式理论已经成为研究诸如障碍、单侧、平衡问题等理论与应用科学中问题的重要工具,例如参考文献[1-8].G. M. Korpelevich[9]提出了求解变分不等式问题(1)的超梯度算法,M. V.Solodov等[10]提出了求解变分不等式问题(1)的二次投影方法,该方法的特点是下一步迭代点是当前迭代点到超平面与可行集合交上的投影,且该超平面严格分离当前迭代点与变分不等式的解集.W. Takahashi等[11]提出了求解变分不等式问题(1)的如下迭代算法:

xi+1=αixi+(1-αi)SΠK(xi-λif(xi)),

(2)

其中{αi}∈(0,1),{λi}∈(0,2λ),S:K→K是一个非扩张映射,Fix(S)表示S的不动点集合.在假设K*∩Fix(S)≠Ø的条件下,文献[11]证明了由(2)式生成的序列{xi}弱收敛到某点x*∈K*∩Fix(S).

受以上研究的启发,本文提出了求解变分不等式(1)的一个新的超梯度算法(见本文算法2.1),在所涉及映射是单调和连续的假定下,证明了算法所产生的序列强收敛到变分不等式问题(1)的解集与一族可数无限非扩张映射不动点集合的公共元素.在算法2.1中，用Li代替文献[6-7,11-12]中的非扩张映射S(Li的定义见(4)和(5)式);与文献[12]的算法A相比,增加了混合投影步骤(见算法2.1的步骤4),从而得到了算法的强收敛结果.此外,算法2.1和文献[12]中算法A的Armijo线性搜索程序也是不同的.

1 预备知识

设H是实的Hilbert空间,其内积和范数分别记为〈x,y〉和‖·‖.用xi⇀x和xi→x分别表示序列{xi}弱收敛和强收敛到x,I为K上的恒等映射.ΠK(x)表示H到K上的投影算子,即对任意的x∈H,存在唯一的ΠK(x)∈K使得

‖x-ΠK(x)‖=inf{‖x-y‖,y∈K}.

引理 1.1[13]1) 〈x-ΠK(x),ΠK(x)-y〉≥0,∀x∈Rn,∀y∈K;

2) ‖ΠK(x)-ΠK(y)‖≤‖x-y‖,∀x,y∈Rn;

3) ‖ΠK(x)-y‖2≤‖x-y‖2-‖x-ΠK(x)‖2,∀x∈Rn,∀y∈K;

4) ‖ΠK(x)-ΠK(y)‖2≤‖x-y‖2-‖ΠK(x)-x+y-ΠK(y)‖2,∀x,y∈Rn.

定义 1.1 称映射f是:1) 单调的,如果

〈x-y,f(x)-f(y)〉≥0, ∀x,y∈K;

2)α-Lipschitz连续的,如果存在常数α≥0,使得

‖f(x)-f(y)‖≤α‖x-y‖, ∀x,y∈K.

定义 1.2 1) 定义f的图像G(f)为

G(f)={(x,y)∈K×K:y=f(x)};

2) 称映射S:K→K为非扩张的,如果

‖S(x)-S(y)‖≤‖x-y‖, ∀x,y∈K.

令

NK(v)={w∈H:〈v-u,w〉≥0,u∈K}.

(3)

定义

则T极大单调的,且0∈T(v)当且仅当v∈K*(见文献[14]).

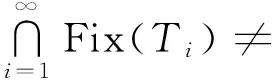
用ωw(xi)表示{xi}的弱聚点集合,即ωw(xi)={x∈H:{xij}弱收敛到x,其中{ij}是{i}的某个子序列}.

引理 1.3[17]设K是H的非空闭凸子集,{xi}是H中的一个序列且x∈H.令u=ΠK(x).如果ωω(xi)⊂K且‖xi-x‖≤‖x-u‖，i=1,2,…,那么xi→u.

Hilbert空间满足Opial条件(参见文献[18]),即如果{xi}弱收敛到x,那么

2 主要结果

令

(4)

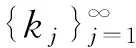
(5)

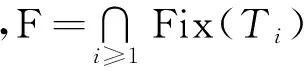
对x∈K0,定义:

r(x):=x-ΠK0(x-f(x)).

(6)

显然,有x∈K*当且仅当r(x)=0.

接下来介绍求解变分不等式(1)的如下混合超梯度算法

算法 2.1 选取x0∈K0,δ∈(0,1),λ∈(0,1).令i=0.

第1步:对xi∈K0,计算

yi=ΠK0(xi-f(xi)),zi=(1-ηi)xi+ηiyi,

其中ηi=γni，ni是满足下面不等式的最小非负整数n:

〈f(xi)-f(xi-γnr(xi)),r(xi)〉≤δ‖r(xi)‖2.

(7)

第2步:计算ti=ΠHi∩K0(xi),其中

Hi={x∈K0|〈x-zi,f(zi)〉≤0}.

第3步:计算

wi=αix0+(1-αi)[βixi+(1-βi)Liti],

其中{αi}⊂(a,b),a,b∈(0,1)且当i→∞时有αi→0,对c,d∈(0,1)有{βi}⊂[c,d].

第4步:计算xi+1=ΠQi∩Mi(x0),其中

Qi={x∈H:‖wi-x‖2≤‖xi-x‖2+

αi(‖x0‖2+2〈xi-x0,x〉)},

Mi={x∈H:〈xi-x,x0-xi〉≥0}.

第5步:若r(xi+1)=0，停止,否则,回到第1步.

以下的3个命题在证明由算法2.1所生成迭代序列的强收敛性中起着关键作用.

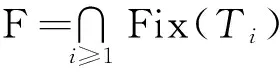
据调查，截至2015年，河南省外出务工人数达1 220万，有82.7万名农村留守儿童。由于缺少父母的关心和引导，留守儿童在为人处世、与人交流及学习等方面都受到了影响。近年来，南阳市各区县不断采取相应措施，加快农村剩余劳动力向城市转移。截至目前，南阳市离家务工者高达240万人，造成了严重的留守儿童问题，所以选择此地作为考查地点具有一定的可行性。

由(4)和(5)式知

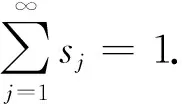
现令x∈F.因对所有的j≥1有x∈Fix(Sj),故

故F⊂Fix(Li).

因为

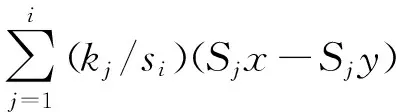
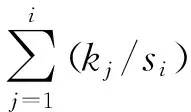
命题 2.2 假设映射f:K0→H是单调和连续的,K*∩F≠Ø.若x*∈K*∩F,则对算法2.1生成的序列{xi}、{wi}、{ti}有

‖xi-x*‖]+αi(‖x0‖2+2〈xi-x0,x*〉),

(8)

‖wi-xi‖[‖wi-x*‖+‖xi-x*‖]+

αi(‖x0‖2+2〈xi-x0,x*〉).

(9)

证明 类似文献[12]定理7的证明有

‖ti-x*‖2≤‖xi-x*‖2-‖xi-ti‖2+

(10)

因为zi=(1-ηi)xi+ηiyi,故

(11)

利用Cauchy-Schwarz不等式有

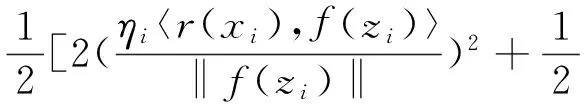
(12)

因此,由(10)～(12)式有

‖ti-x*‖2≤‖xi-x*‖2-‖xi-ti‖2-

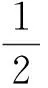
由x*∈K*∩F和F⊂Fix(Li)知x*∈Fix(Li).所以

‖wi-x*‖2≤αi‖x0-x*‖2+(1-αi)βi‖xi-x*‖2+

(1-αi)(1-βi)‖Liti-x*‖2≤

αi‖x0-x*‖2+(1-αi)βi‖xi-x*‖2+

(1-αi)(1-βi)‖ti-x*‖2≤

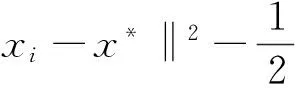
αi‖x0-x*‖2+(1-αi)‖xi-x*‖2-

‖xi-x*‖2+αi(‖x0‖2+2〈xi-x0,x*〉)-

(13)

根据(13)式,对所有的i∈N有

‖xi-ti‖2≤‖xi-x*‖2-

‖wi-x*‖2+αi(‖x0‖2+2〈xi-x0,x*〉)≤

‖wi-xi‖[‖wi-x*‖+‖xi-x*‖]+

αi(‖x0‖2+2〈xi-x0,x*〉).

再次运用Cauchy-Schwarz不等式得到

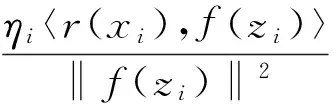
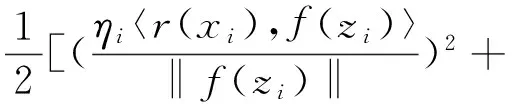
(14)

由此,从(10)、(11)和(14)式可得

‖wi-x*‖2≤αi‖x0-x*‖2+(1-αi)βi‖xi-x*‖2+

αi‖x0-x*‖2+(1-αi)‖xi-x*‖2-

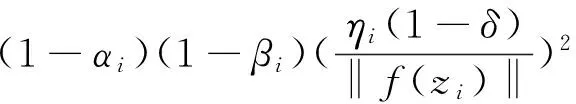
‖xi-x*‖2+αi(‖x0-x*‖2-‖xi-x*‖2)-

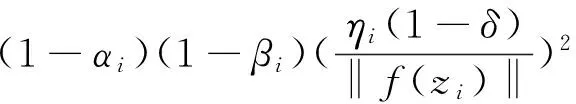
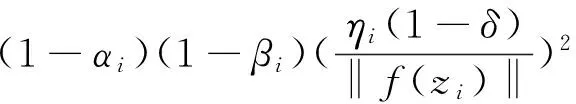
‖xi-x*‖2+αi(‖x0‖2+2〈xi-x0,x*〉)-

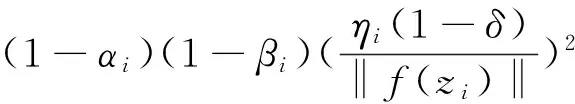
(15)

因此,由(15)式得到不等式(9).

命题 2.3 若K*∩F≠Ø,则:

1)xi+1有定义;

2) ‖xi-x0‖≤‖xi+1-x0‖≤‖x0-ΠK*∩F(x0)‖.

证明 1) 只需证明Mi∩Qi是Hilbert空间中的非空闭凸集.首先,证明对任意的i∈N,Mi∩Qi是闭凸的.显然，对任意的i∈N,Mi是闭凸的且Qi是闭的.因为

‖wi-x‖2≤‖xi-x‖2+

αi(‖x0‖2+2〈xi-x0,x〉),

等价于

〈(1-αi)xi+αix0-wi,x〉≤〈xi-wi,xi〉-

因此,Qi是凸的.接着证明Mi∩Qi是非空的.假设K*∩F⊂Mi.因为xi+1=ΠQi∩Mi(x0)，所以,对所有z∈K*∩F⊂Qi∩Mi有〈xi+1-x0,z-xi+1〉≥0,因此K*∩F⊂Mi+1.故得证.

2) 由于

〈xi-x,x0-xi〉≥0, ∀x∈Mi,

所以xi=ΠMi(x0).由xi+1∈Mi知

‖xi-x0‖=‖ΠMi(x0)-x0‖≤‖xi+1-x0‖.

(16)

注意ΠK*∩F(x0)∈K*∩F⊂Mi+1,因此

‖xi+1-x0‖=‖ΠMi+1(x0)-x0‖≤

‖ΠK*∩F(x0)-x0‖.

(17)

故根据(16)和(17)式有

‖xi-x0‖≤‖xi+1-x0‖≤‖x0-ΠK*∩F(x0)‖.

下面的定理说明由算法2.1生成的序列{xi}强收敛到K*∩F的某个元素.

证明 根据引理1.3和命题2.3的2),只需证明ωω(xi)⊂K*∩F.分4步证明我们的结论.

第1步:‖xi+1-xi‖→0,‖wi-xi‖→0,‖xi-ti‖→0,‖Lixi-xi‖→0.

在引理1.1的3)中令y=xi+1和x=x0有

‖xi+1-xi‖2≤‖xi+1-x0‖2-‖xi-x0‖2.

(18)

因此

‖xi+1-xi‖→0,i→0.

(19)

由xi+1∈Qi有

‖wi-xi+1‖2≤‖xi-xi+1‖2+

αi(‖x0‖2+2〈xi-x0,xi+1〉).

(20)

因为{xi}有界且αi→0,i→0,所以由(19)和(20)式有‖wi-xi+1‖→0,i→0.从而

‖wi-xi‖→0.

(21)

由{xi}有界知{wi}有界.因为{αi}⊂(a,b)(a,b∈(0,1))且{βi}⊂[c,d](c,d∈(0,1)),所以,从(8)和(21)式可得

‖xi-ti‖→0.

(22)

因为

所以

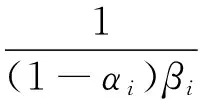
(23)

由于Li是非扩张的且x*∈Fix(Li),所以

‖Liti-x0‖≤‖Liti-x*‖+‖x*-x0‖≤

‖Liti-Lix*‖+‖x*-x0‖≤

‖ti-x*‖+‖x*-x0‖.

因此,从{ti}有界可知‖Liti-x0‖有界.从而由(23)式知

‖Liti-xi‖→0.

(24)

因为

‖Lixi-xi‖≤‖Lixi-Liti‖+‖Liti-xi‖≤

‖xi-ti‖+‖Liti-xi‖,

故从(22)和(24)式可知

‖Lixi-xi‖→0.

(25)

第2步:令(v,u)∈G(T),则u∈T(v)=NK(v)+f(v),从而u-f(v)∈NK(v).因此

〈v-x,u-f(v)〉≥0, ∀x∈K.

(26)

令x=xi-f(xi)，y=v,由引理1.1的1)知〈xi-f(xi)-ΠK(xi-f(xi)),ΠK(xi-f(xi))-v〉≥0,即

〈xi-f(xi)-yi,yi-v〉≥0.

(27)

因为ti∈K,故由(26)式有

〈v-ti,u-f(v)〉≥0.

(28)

根据{xi}的有界性和f的连续性知,{yi}、{zi}和{f(zi)}是有界的.根据{αi}和{βi}的假设,由(9)式知

‖r(xi)‖2=0.

(29)

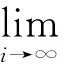
‖xij-yij‖=0,

(30)

和

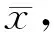
(31)

由于‖yij-tij‖≤‖yij-xij‖+‖xij-tij‖,故由(22)和(30)式知

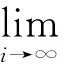
‖yij-tij‖=0.

(32)

从而由(28)式可得

〈v-tij,u〉≥〈v-tij,f(v)〉≥〈v-tij,f(v)〉-

〈xij-f(xij)-yij,yij-v〉=

〈v-tij,f(v)-f(tij)〉+〈v-tij,f(tij)〉-

〈v-yij,yij-xij〉-〈v-yij,f(xij)〉≥

〈v-tij,f(tij)〉-〈v-yij,yij-xij〉-

〈v-yij,f(xij)〉,

(33)

其中最后一个不等式可根据f的单调性得到.

由于f是连续的,对(33)式取极限有

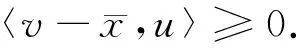
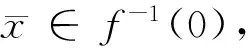
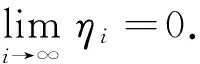
δ‖r(xi)‖2<〈f(xi)-f(xi-γni-1r(xi))〉=

〈f(xi)-f(xi-γ-1ηir(xi))〉.

(34)

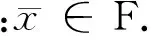
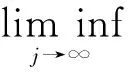
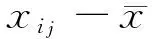
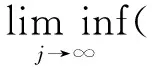
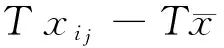
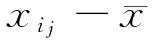
(35)

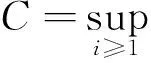
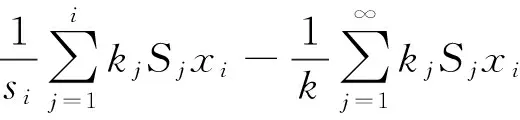
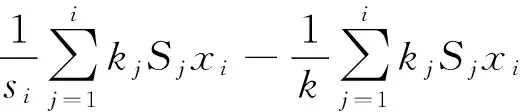
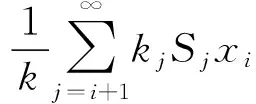
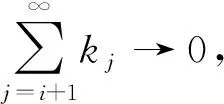
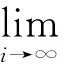
‖Lixi-Txi‖=0.

(36)

因此由(25)和(36)式可得

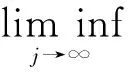
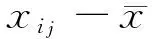
矛盾,故得证.

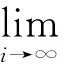
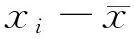
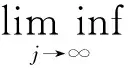
矛盾,故得证.

[1] Facchinei F, Pang J S. Finite-Dimensional Variational Inequalities and Complementary Problems[M]. New York:Springer-Verlag,2003.

[2] Fang C J, He Y R. A double projection algorithm for multi-valued variational inequalities and a unified framework of the method[J]. Appl Math Comput,2011,217:9543-9511.

[3] Fang C J, He Y R. An extragradient method for generalized variational inequality[J]. Pacific J Optimization,2013,9:47-59.

[4] Fang C J, Chen S L. A subgradient extragradient algorithm for solving multi-valued variational inequality[J]. Appl Math Comput,2014,229:123-130.

[5] Fang C J, Chen S L. A projection algorithm for set-valued variational inequalities on Hadamard manifolds[J]. Optimization Letters,2015,9:779-794.

[6] Iiduka H, Takahashi W. Strong convergence theorems for nonexpansive nonself-mappings and inverse-strongly-monotone mappings[J]. J Convex Analysis,2004,11(1):69-79.

[7] Nadezhkina N, Takahashi W. Strong convergence theorem by a hybrid method for nonexpansive mappings and Lipschitz-continuous monotone mappings[J]. SIAM J Optimization,2006,16(4):1230-1241.

[8] Thuy N T T. A new hybrid method for variational inequality and fixed point problems[J]. Vietnam J Mathematics,2013,41(3):353-366.

[9] Korpelevich G M. The extragradient method for finding saddle points and other problems[J]. Matecon,1976,12:747-756.

[10] Solodov M V, Svaiter B F. A new projection method for variational inequality problems[J]. SIAM J Control and Optimization,1999,37(3):765-776.

[11] Takahashi W, Toyoda M. Weak convergence theorems for nonexpansive mappings and monotone mappings[J]. J Optimization Theory and Applications,2003,118(2):417-428.

[12] Wang X, Li S, Kou X. An extension of subgradient method for variational inequality problems in Hilbert space[J]. Abstract and Applied Analysis,2013:2013.

[13] Zarantonello E H. Projections on Convex Sets in Hilbert Space and Spectral Theory:Contributions to Nonlinear Functional Analysis[M]. New York:Academic Press,1971.

[14] Rockafellar R T. On the maximality of sums of nonlinear monotone operators[J]. Transactions of the American Mathematical Society,1970,149:75-88.

[15] Bruck Jr R E. Properties of fixed point sets of nonexpansive mappings in Banach spaces[J]. Transactions of the American Mathematical Society,1973,179:251-262.

[16] He S, Guo J. Iterative algorithm for common fixed points of infinite family of nonexpansive mappings in Banach spaces[J]. J Appl Math,2012:2012.

[17] Goebel K, Kirk W A. Topics in Metric Fixed Point Theory[M]. Cambridge:Cambridge University Press,1990.

[18] Opial Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings[J]. Bulletin of the American Mathematical Society,1967,73(4):591-597.

2010 MSC:49J40

(编辑 余 毅)

A New Algorithm for Variational Inequality Problems in a Hilbert Space

FANG Changjie, WANG Ying
(CollegeofScience,ChongqingUniversityofPostsandTelecommunications,Chongqing400065)

In this paper, we present a hybrid extragradient method for variational inequality problems in a Hilbert space. Under the assumption thatfis a continuous and monotone mapping, we prove that the sequence generated by our method converges strongly to the common element of solutions of the variational inequality problem and fixed point set of a countably infinite family of nonexpansive mappings in Hilbert spaces.

variational inequality; fixed point; nonexpansive mapping; continuous mappings; monotone mapping; strong convergence

2015-05-18

国家自然科学基金(11426055)、重庆市自然科学基金基础与前沿研究计划项目基金(CSTC2014JCYJA00044)

方长杰(1974—),男,副教授,主要从事非线性泛函方向的研究,E-mail:fangcj@cqupt.edu.cn

O177.92; O178

A

1001-8395(2015)06-0824-06

10.3969/j.issn.1001-8395.2015.06.006