Hadamard流形上极大单调向量场奇点的Mann迭代算法
2015-05-04唐国吉夏福全广西民族大学理学院广西南宁530006江西财经大学信息管理学院江西南昌33003四川师范大学数学与软件科学学院四川成都60066
唐国吉, 汪 星, 夏福全(. 广西民族大学 理学院, 广西 南宁 530006; . 江西财经大学 信息管理学院, 江西 南昌 33003;3. 四川师范大学 数学与软件科学学院, 四川 成都 60066)
Hadamard流形上极大单调向量场奇点的Mann迭代算法
唐国吉1, 汪 星2, 夏福全3*
(1. 广西民族大学 理学院, 广西 南宁 530006; 2. 江西财经大学 信息管理学院, 江西 南昌 330013;3. 四川师范大学 数学与软件科学学院, 四川 成都 610066)
通过组合邻近点算法和Mann迭代技术,构造了求解Hadamard流形上极大单调向量场奇点的一个新方法,其中邻近点子问题允许非精确的计算.在适当的假设下,证明了新算法产生的序列收敛于极大单调向量场的一个奇点.主要结果推广和改善了近年的一些文献的相关结果.
极大单调向量场; 邻近点算法; Mann迭代; Hadamard流形
单调算子理论是非线性分析的重要组成部分.在单调算子理论中,一个基本的问题是寻找极大单调算子的零点,即找x∈H使得
0∈A(x),
(1)
其中A是Hilbert空间H到其自身的一个极值单调算子.为了方便,把算子A在H中所有的零点作成的集合记为A-1(0).
求解问题(1)的一个常用方法是邻近点算法.对于任意给定的一个初始点x0∈H,邻近点算法按照法则
0∈A(xn+1)+λn(xn+1-xn),
(2)
产生序列{xn},其中λn是一个正的实数列.1976年,R. T. Rockafellar[1]在适当的条件下证明了按法则(2)产生的序列弱收敛于A-1(0)中的一个元.此后,邻近点算法的研究引起了众多学者的关注.他们从不同角度(如不同的空间框架:有限维欧式空间、Hilbert空间、Banach空间、Hadamard流形、Riemann流形等;不同的研究对象:变分不等式、最优化问题、均衡问题等)对邻近点算法展开研究,并取得了丰富的成果.

(3)
C. Li等[2]证明了相应的收敛性结果.
正如C. Li等[2]指出的那样,把适用于欧式空间的一些概念和技巧推广到Riemann流形是一种自然的想法,但这些工作又是不平凡的.近年来,一些学者在Riemann流形(或Hadamard流形)上研究变分包含、变分不等式和优化问题,如文献[2-25].
在线性空间的框架下,受寻找一些映像的不动点的方法的启发,一些学者(如文献[26-29])设计了邻近Halpern型方法和邻近Mann型方法来求解问题(1).这类方法都已经证明了拥有较好的收敛性质.
最近,J. H. Wang等[24]在Hadamard流形上构造了一个邻近Halpern型方法来求解极大单调向量场的奇点.在适当的条件下,他们证明了算法产生的序列收敛于极大单调向量场的离初始点最近(按Riemann度量的意义)的奇点.另一方面,C. Li等[12]在Hadamard流形上构造了2种迭代算法(即Halpern型迭代和Mann型迭代)来求解非扩张映像的不动点.从他们提供的数值例子可以看出,Mann型迭代比Halpern型迭代具有更快的收敛速度.一个自然的问题是:是否能通过组合邻近点算法和Mann型迭代设计一种新的方法来求解极大单调向量场的奇点.这是本文的主要动机之一.
到现在为止,Riemann流形上大多数的邻近点算法(如文献[2,5,7,10,18-19,21])都是精确迭代的版本.然而,因为邻近点算法本质上是隐迭代方法,因此在每个迭代中精确求解子问题的代价是昂贵的.正如E. A. P. Quiroz等[19]所指出的那样,为了计算的可实现性,在流形框架下分析非精确迭代算法的收敛性是重要的.这是本文的另一个主要动机.
受以上文献的启发,在本文中通过组合邻近点算法和Mann型迭代,设计了一个求解Hadamard流形上极大单调向量场的奇点的新方法,其中邻近点子问题允许非精确的计算.在适当的条件下,证明了新方法产生的序列收敛于极大单调向量场的一个奇点.
1 预备知识
为了读者方便,在这一节中回顾一下Riemann流形的一些基本定义,性质和记号,这些内容在任何一本Riemann几何的教材(如[30])中都能找到.
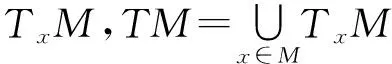
一个Riemann流形称为是完备的是指对于每一点x∈M,从x出发的所有测地线对于每一个-∞ 假设M是完备的,在点x的指数映射expx:TxM→M是指对每一个v∈TxM有expxv=γv(1,x),其中γ(·)=γv(·,x)起于点x速度为v的测地线.那么对每一个实数t有expxtv=γv(t,x).对每一个点x∈M,expx在TxM上是可微的. 一个完备的,单连通且具有非正截面曲率的Riemann流形称为Hadamard流形.以下假设M是一个m维Hadamard流形.下面的结果是众所周知的(如参见文献[30]的定理4.1). 命题 1.1 设M是一个Hadamard流形且p∈M,那么expp:TpM→M是一个微分同胚,并且对于任意两点p,q∈M,存在连接p到q的唯一正规测地线. 这个命题说明M微分同胚于欧氏空间Rm.这样,容易看到M与Rm有同样的拓扑和微分结构.此外,Hadamard流形与欧氏空间有一些类似的几何性质.下面的命题取自于文献[30]的命题4.5,它将在本文的研究中起重要的作用.回顾Riemann流形中的测地三角形△(p1p2p3)是指由三点p1,p2和p3,以及连接这3个点的最小测地线组成的集合. α1+α2+α3≤π, (4) (5) 由 d(pi,pi+1)d(pi+1,pi+2)cosαi+1 不等式(5)可写为 d2(pi,pi+1)+d2(pi+1,pi+2)- (6) 一个子集K⊆M称为是凸的,如果K中任意两点p和q,连接p到q的测地线都包含于K,即如果γ:[a,b]→M是一条测地线使得p=γ(a)和q=γ(b),那么对于所有的t∈[0,1]都有γ((1-t)a+tb)∈K. 函数f:M→R称为是凸的,如果对于M上的任意测地线γ,复合函数f∘γ:R→R是凸的,即对任意的a,b∈R和0≤t≤1,有 (f∘γ)(ta+(1-t)b)≤ t(f∘γ)(a)+(1-t)(f∘γ)(b). 下面的命题说明距离函数是凸的. 命题 1.3[30]设d:M×M→R是距离函数,那么d关于乘积Riemann度量是凸函数,即对于任给的测地线γ1:[0,1]→M和γ2:[0,1]→M和所有的t∈[0,1]有如下不等式成立: d(γ1(t),γ2(t))≤ (1-t)d(γ1(0),γ2(0))+td(γ1(1),γ2(1)). 特别地,对每一个p∈M,函数d(·,p):M→R是一个凸函数. 引理 1.1[8]设△(pqr)是M上的一个测地三角形,那么存在p′,q′,r′∈R2使得 d(p,q)=‖p′-q′‖,d(q,r)=‖q′-r′‖, d(r,p)=‖r′-p′‖. 引理 1.2[12]设△(pqr)是M中的测地三角形,△(p′q′r′)是其比较三角形. 1) 设α,β,γ(分别地,α′,β′,γ′)是△(pqr)(分别地,△(p′q′r′))在顶点p,q,r(分别地,p′,q′,r′)的三个角,那么 α′≥α,β′≥β,γ′≥γ. 2) 任意给定连接p到q的测地线上的点z,z′是线段[p′,q′]上满足d(z,p)=‖z′-p′‖和d(z,q)=‖z′-q′‖的点(称为z的比较点),那么有不等式 d(z,r)≤‖z′-r′‖. 把所有满足定义域D(A)是闭凸集的集值向量场A:M→2TM(即对每个x∈M有A(x)⊆TxM)记为X(M),其中A的定义域D(A)是 D(A)={x∈M:A(x)≠Ø}. 定义 1.1 设A∈X(M)是一个向量场,那么称A是: (i) 单调的,如果对于任意的x,y∈D(A), ∀u∈A(x), ∀v∈A(y); (ii) 强单调的,如果存在ρ>0使得对于任意的x,y∈D(A), ∀u∈A(x), ∀v∈A(y); (iii) 极大单调的,如果它是单调的且对于任意的x∈D(A)和u∈TxM有如下蕴含关系成立: ∀y∈D(A), v∈A(y)⟹u∈A(x). Hadamard流形上向量场的Kuratowski半连续性概念由C.Li等[2]引入. 定义 1.2 设A∈X(M),x0∈D(A).A称为: (b) 在M上是Kuratowski上半连续的,如果对于每一个点x0∈D(A),A在点x0是Kuratowski上半连续的. 由文献[2]中定理3.7可知: 注 1.1 如果A极大单调且D(A)=M,那么A是Kuratowski上半连续的. 现在正式给出的算法.令δ∈(0,1). 算法 2.1 初始化:设x0∈M任意取定. 迭代过程:对于给定的xn∈M,选取参数λn>0和元素yn∈M使得 (7) 选取误差εn≥0和元素zn∈M使得 d(zn,yn)≤εn. (8) 选取αn∈[0,1-δ]并通过下式定义xn+1, (9) 或等价地, xn+1=γn(1-αn), (10) 其中γn:[0,1]→M是连接xn到zn的测地线(即γn(0)=xn和γn(1)=zn). 注 2.1 注意到算法2.1中的(7)式是一个隐迭代.这样一个基本的问题是说明这个步骤是可定义的.事实上,对每个n,定义Bn∈X(M)如下: ∀x∈D(A), 那么当A∈X(M)是单调时,每个Bn是强单调的.完全类似于文献[2]中的注4.4,知道如果A是极大单调向量场且D(A)=M,那么(7)式是可定义的,从而算法2.1是良定的. 注 2.2 (i) 如果M=Rn,那么算法2.1退化为文献[29]中的算法5.2当Hilbert空间是有限维的情形.因此,算法2.1可看成文献[29]中的算法5.2从线性空间到Hadamard流形的推广. (ii) 如果εn=0且αn=0,那么算法2.1退化为Hadamard流形上的精确邻近点算法(参见文献[2]中(4.3)式). (iii) 与文献[24]中的算法MP作比较,在迭代过程中,邻近子问题(7)式和相应的误差容忍(8)式是一样的.不同之处在于(9)式是Mann型迭代过程,而文献[24]中的对应部分是Hapern型迭代,即 (iv) 与C. Li等[12]提出的Hadamard流形上非扩张映像不动点的Mann迭代算法相比较,其关于松弛因子αn的条件与本文算法2.1的不一样.文献[12]中{αn}要求满足 ∞. (11) 容易看到的条件比上述条件要弱.比如取αn=1/n2时,(11)式就不成立了.由于条件(11)在Mann型迭代方法的收敛性证明中发挥关键作用,因此在Mann型迭代方法中考虑如何减弱松弛因子的限制条件是重要的.因此为了去掉条件(11),在收敛性分析中采用了与文献[12]中完全不一样的技巧. 接着,给出算法2.1的收敛性结果. 定理 2.1 设{xn}是由算法2.1产生的序列.假设 (12) 那么{xn}收敛于A-1(0)中的一个点. 证明 把证明过程分几步完成. 第1步:证明序列{xn}是有界的. (13) 考虑测地三角形△(xnynz).由命题1.2可得 d2(yn,z)+d2(yn,xn)- 结合(13)式可得 d2(yn,z)+d2(yn,xn)≤d2(xn,z). (14) 这样,容易看出 d(yn,z)≤d(xn,z). (15) 由命题1.3可得 d(xn+1,z)=d(γn(1-αn),z)≤ αnd(γn(0),z)+(1-αn)d(γn(1),z)≤ αnd(xn,z)+(1-αn)d(zn,z). (16) d(zn,z)≤d(yn,z)+d(yn,zn)≤ d(xn,z)+εn. (17) d(xn+1,z)≤ αnd(xn,z)+(1-αn)d(xn,z)+(1-αn)εn≤ d(xn,z)+εn. (18) 第2步:证明 (19) 事实上,由距离的三角不等式和(8)~(9)式可得 d(xn+1,yn)≤d(xn+1,zn)+d(zn,yn)≤ αnd(xn,zn)+εn. (20) 应用引理1.2的2)可得 αnd2(xn,z)+(1-αn)d2(zn,z)- αn(1-αn)d2(xn,zn). (21) 由(15)式和(8)式可得 d2(zn,z)≤[d(yn,z)+d(yn,zn)]2≤ [d(xn,z)+εn]2≤ d2(xn,z)+εnC, (22) d2(xn+1,z)≤d2(xn,z)+(1-αn)εnA- αn(1-αn)d2(xn,zn). 结合条件αn∈[0,1-δ]可得到 δαn2d2(xn,zn)≤αn(1-αn)d2(xn,zn)≤ d2(xn,z)-d2(xn+1,z)+εnA. 第3步:证明{xn}的每一个聚点属于A-1(0). (24) 由(7)式可知,对每一个k,有unk-1∈A(ynk-1).由于A是极大单调的,根据注1.1可知A是Kuratowski上半连续的.再结合(24)式可得0∈A-1(0). 由命题1.2可得 (25) (26) 注 2.3 定理2.1从以下方面推广和改善了一些新近的结果. (i) 如果M=Rn,那么定理2.1退化为文献[29]的定理5.2中当Hilbert空间是有限维的情形. (ii) 如果算法2.1中εn=0且αn=0,那么定理2.1退化为Li等人的主要结果(参见文献[2]的推论4.8). [1] Rockafellar R T. Monotone operators and the proximal point algorithm[J]. SIAM J Control Optim,1976,14:877-898. [2] Li C, López C, Martin-Mrquez V. Monotone vector fields and the proximal point algorithm on Hadamard manifolds[J]. J London Math Soc,2009,79:663-683. [3] Agarwal R P, Ahmad I, Iqbal A, et al. Generalized invex sets and preinvex functions on Riemannian manifolds[J]. Taiwan J Math,2012,16:1719-1732. [5] Bento G C, Ferreira O P, Oliveira P R. Local convergence of the proximal point method for a special class of nonconvex functions on Hadamard manifolds[J]. Nonlinear Anal,2010,73:564-572. [6] Bento G C, Melo J G. Subgradient method for convex feasibility on Riemannian manifolds[J]. J Optim Theory Appl,2012,152:773-785. [7] Bento G C, Ferreira O P, Oliveira P R. Proximal point method for a special class of nonconvex functions on Hadamard manifolds[J]. Optimization,2015,64:289-319. [8] Bridson M, Haefliger A. Metric Spaces of Non-Positive Curvature[M]. Berlin:Springer-Verlag,1999. [9] Ferreira O P, Oliveira P R. Subgradient algorithm on Riemannian manifolds[J]. J Optim Theory Appl,1998,97:93-104. [10] Ferreira O P, Oliveira P R. Proximal point algorithm on Riemannian manifolds[J]. Optimization,2002,51:257-270. [11] Ferreira O P, Pérez L R L, Németh S Z. Singularities of monotone vector fields and an extragradient-type algorithm[J]. J Glob Optim,2005,31:133-151. [12] Li C, López G, Martin-Mrquez V. Iterative algorithms for nonexpansive mappings on Hadamard manifolds[J]. Taiwan J Math,2010,14:541-559. [13] Németh S Z. Geodesic monotone vector fields[J]. Lobachevskii J Math,1999,5:13-28. [14] Németh S Z. Monotonicity of the complementary vector field of a nonexpansive map[J]. Acta Math Hungar,1999,84:189-197. [15] Németh S Z. Monotone vector fields[J]. Publ Math Debrecen,1999,54:437-449. [16] Németh S Z. Variational inequalities on Hadamard manifolds[J]. Nonlinear Anal,2003,52:1491-1498. [17] Quiroz E A P, Quispe E M, Oliveira P R. Steepest descent method with a generalized Armijo search for quasiconvex functions on Riemannian manifolds[J]. J Math Anal Appl,2008,341:467-477. [18] Quiroz E A P, Quispe E M, Oliveira P R. Proximal point methods for quasiconvex and convex functions with Bregman distances on manifolds[J]. J Convex Anal,2009,16:49-69. [19] Quiroz E A P, Oliveira P R. Proximal point method for minimizing quasiconvex locally Lipschitz functions on Hadamard manifolds[J]. Nonlinear Anal,2012,75:5924-5932. [20] Tang G J, Huang N J. Korpelevich’s method for variational inequality problems on Hadamard manifolds[J]. J Glob Optim,2012,54:493-509. [21] Tang G J, Zhou L W, Huang N J. The proximal point algorithm for pseudomonotone variational inequalities on Hadamard manifolds[J]. Optim Lett,2013,7:779-790. [22] Tang G J, Huang N J. An inexact proximal point algorithm for maximal monotone vector fields on Hadamard manifolds[J]. Oper Res Lett,2013,41:586-591. [23] Tang G J, Wang X, Liu H W. A projection-type method for variational inequalities on Hadamard manifolds and verification of solution existence[J]. Optimization,2015,64(5):1081-1096. [24] Wang J H, López G. Modified proximal point algorithms on Hadamard manifolds[J]. Optimization,2011,60:697-708. [25] Zhou L W, Huang N J. Existence of solutions for vector optimization on Hadamard manifolds[J]. J Optim Theory Appl,2013,157:44-53. [26] Kamimura S, Takahashi W. Approximating solutions of maximal monotone operators in Hilbert spaces[J]. J Approx Theory,2000,106:226-240. [27] Kamimura S, Kohsaka F, Takahashi W. Weak and strong convergence theorems for maximal monotone operators in a Banach space[J]. Set-Valued Anal,2004,12:417-429. [28] Kamimura S, Takahashi W. Weak and strong convergence of solutions to accretive operator inclusions and applications[J]. Set-Valued Anal,2000,8:361-374. [29] Xu H K. Iterative algorithms for nonlinear operators[J]. J London Math Soc,2002,66:240-256. [30] Sakai T. Riemannian geometry[C]//Translations of Mathematical Monographs, 149. Providence:American Mathematical Society,1996. 2010 MSC:53C25; 47J25 (编辑 周 俊) A Mann Type Iterative Scheme for Singularities of Maximal Monotone Vector Fields on Hadamard Manifolds TANG Guoji1, WANG Xing2, XIA Fuquan3 In this paper, by combining the techniques of the proximal point algorithm and Mann-type iteration, a method is proposed for finding the singularities of maximal monotone vector fields on Hadamard manifolds, where the proximal subproblem steps allow inexact computation. Under suitable assumptions, we prove the sequence generated by the proposed method converges to a singularity of maximal monotone vector fields on Hadamard manifolds. The main results presented in this paper generalize and improve some corresponding known results given in literatures. maximal monotone vector field; proximal point algorithm; Mann iteration; Hadamard manifold 2015-01-16 国家自然科学基金(11426119)、教育部重点项目(212147)、广西自然科学基金(2013GXNSFBA019015)、广西教育厅科研重点项目(ZD2014045)和广西高校优秀中青年骨干教师培养工程(桂教人2014-39) O221.2 A 1001-8395(2015)06-0818-06 10.3969/j.issn.1001-8395.2015.06.005 *通信作者简介:夏福全(1973—),男,教授,主要从事变分不等式与最优化理论的研究,E-mail:fuquanxia@sina.com

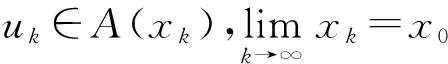
2 Mann迭代算法
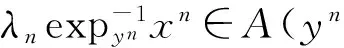

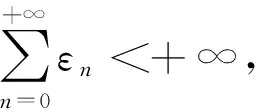
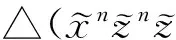

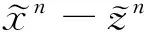



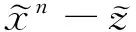
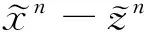







(1.CollegeofScience,GuangxiUniversityforNationalities,Nanning530006,Guangxi;2.CollegeofInformationAdministration,JiangxiUniversityofFinanceandEconomics,Nanchang330013,Jiangxi;3.InstituteofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)
