车辆路径问题的快速多邻域迭代局部搜索算法

刘万峰，李 霞

1)深圳大学信息工程学院，深圳 518060; 2)深圳市现代通信与信息处理重点实验室，深圳 518060

【电子与信息科学 / Electronics and Information Science】

车辆路径问题的快速多邻域迭代局部搜索算法

刘万峰1，2，李 霞1，2

1)深圳大学信息工程学院，深圳 518060; 2)深圳市现代通信与信息处理重点实验室，深圳 518060

对于容量约束的车辆路径问题 (capacitated vehicle routing problem，CVRP)以及容量和最大行驶距离约束的车辆问题(capacitated and distance constrained vehicle routing problem，CDVRP) ，邻域解的评估包含了适应值计算及合法性评估．设计一种可变长编码的可行解表示，提出用于CVRP/CDVRP问题的邻域解合法性快速评估策略．该策略针对交换、插入、2-opt和2-opt*四种常用的局部搜索算子，通过引入前载重、后载重、前向距离和后向距离的概念，实现了邻域解合法性的快速评估．将改进后的局部搜索算子与迭代局部搜索(iterated local search, ILS)算法相结合，提出用于车辆路径问题的快速多邻域迭代局部搜索(fast multi-neighborhood ILS，FMNILS)算法．该快速评估策略将评估一个邻域解的时间复杂度由O(N)降至O(1)，算法仿真结果表明，FMNILS算法运算能力的提高大致与配送路线所服务的客户数成正比；对客户数介于200～500的容量/最大距离约束VRP问题，该算法能在短时间内获得较满意解，平均求解精度1.2%以内，平均耗时约96s，仅为对比算法的6%或更少．

人工智能；启发式算法；车辆路径问题；多邻域；迭代局部搜索；可变长编码

1959年，Laporte等[1]提出车辆路径问题(vehicle routing problem，VRP)．由于其重要的实际意义和难于求解，VRP问题一直是运筹学与组合优化领域的研究热点．VRP的研究目标是对给定的客户设计适当的配送路线，在满足车辆容量、最大行驶距离和时间窗等约束条件下，实现使用车辆数最少、运输成本最小等优化目标． VRP是NP-完全(NP-complete)问题，即使是最简单的容量约束车辆路径问题(capacitated VRP，CVRP)，现有文献也只给出了客户数约为100时的CVRP问题的精确求解[2]．因此，设计一个能在可接受时间内获得较好解的启发式算法是该问题的主要研究方向之一．

近年来，许多学者对启发式算法求解CVRP问题进行了研究，并提出很多优秀的算法．迭代局部搜索(iterated local search, ILS)算法结构简单且有效；可变邻域方法(variable neighborhood)易于发现当前解邻域范围内的更好解，这两种方法通常结合在一起，用于CVRP问题的求解．Chen等[3]提出一种基于多种局部优化算子的迭代变邻域下降算法(iterated variable neighborhood descent，IVND)；Subramanian等[4-5]将集合划分(set partitioning，SP)、RVND(variable neighborhood descent with random neighborhood ordering)和ILS相结合设计了ILS-RVND-SP算法．Li等[6]在RTR(record-to-record)算法中采用了可变长度的邻域列表，用于指导算法的搜索方向．相比单一算法，混合算法往往能获得更好的结果．骆剑平等[7]将幂律极值动力学优化(power law extremal optimization，τ-EO)融合于混合蛙跳算法(shuffled frog leaping algorithm，SFLA)，针对CVRP 对τ-EO 过程进行重新设计，提出新颖的组元适应度计算方法并根据幂律概率分布来挑选需要变异的组元．Wink等[8]提出了一种结合了CVRP特定知识和启发式算法的混合遗传算法，并在算法的参数优化中也采用了遗传算法．为减少VRP问题求解算法的计算复杂度，Zachariadis等[9]将当前解和其所有邻域解的差异保存在SMD(static move descriptor)的数据结构中，从而避免了适应值差异的重复计算并提高了算法的运行效率．随着计算机硬件的快速发展，近年涌现了许多求解CVRP问题的并行算法．Chrisgro⊇r等[10]提出一种结合启发式局部搜索和整数规划的并行算法；Jin等[11]提出一种多邻域的并行禁忌搜索算法．

以上算法在求解VRP问题时均需要反复对解个体进行评估，对解个体的评估包括合法性评估和适应值计算，该评估占用了算法的大部分运行时间．对于规模为N的VRP问题，解个体评估的计算复杂度为O(N)，随着问题规模的增加，计算复杂度线性增加．在一些组合优化问题中，局部搜索算法对邻域解的评估只需要计算其与当前解的差异，从而极大地减少了适应值的计算复杂度[12]．例如，在TSP问题中，计算邻域解和当前解的适应值差异的复杂度为O(1)，而解的适应值的计算复杂度为O(N)[12]． 由于VRP问题中常存在车辆容量、最大行驶距离等约束条件，采用局部搜索算法获得的邻域解多出现非法解，仅通过计算邻域解的适应值差异并不能实现对邻域解的正确评估．本研究通过引入前载重、后载重、前向距离和后向距离的概念，将当前解与车辆容量、最大行驶距离约束相关的信息分解到各客户节点，依据客户节点的约束信息对多种常用的局部搜索算子实现邻域解合法性的快速评估，将邻域解评估(包括合法性评估及适应值计算)的计算复杂度由O(N)减小为O(1)．基于此，本研究提出一种快速多邻域迭代局部搜索算法(fastmulti-neighborhoodILS，FMNILS)．该算法中设计了一种新颖的可变长编码的可行解表示，使算法在优化过程中可同时实现对车辆数和运输成本的优化.为克服单一邻域寻优能力的不足，使用4种不同的邻域结构，设计了和局部搜索算法相适应的扰动策略，使算法易于跳出局部最优．通过与相关文献算法比较，该算法在CVRP和CDVRP基准测试问题上能在很短的时间内找到较好解．

1 车辆路径问题及可行解编码

VRP的研究目标是对给定的客户设计适当的配送路线，在满足车辆容量、最大行驶距离、时间窗等约束条件下，实现使用车辆数最少、运输成本最小(本研究针对的VRP问题的运输成本以车辆的行驶距离来表示)等优化目标．VRP问题可描述为：给定一个完全图G=(V，E)，其中，V={v0,v1, …,vi, …,vN}是节点集合，N为客户总数，v0表示仓库，vi(i=1, 2, …,N) 是第i个客户节点，其配送需求为di；E={vi，vj|vi，vj∈V)是连接各节点的弧的集合，从节点vi到节点vj的运输成本cij>0． 配送车辆从仓库出发并最终返回仓库，每个客户须由且只能由一辆配送车进行服务．不失一般性，在CVRP和CDVRP问题中，假设每辆车所能运载的最大载重相等，均用Q表示，即车辆容量约束；此外，每条配送路线的最大行驶距离也相同，均用D表示，即最大行驶距离约束．

在本研究中，VRP问题的解采用可变长编码方式(variablelengthcoding，VLC)．对于有N个客户的VRP问题，其可行解可表示为

S=(s1,s2,…,si,…,sM),

(1)

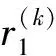
1)配送路线R(1)：0，1，3，6，8，0；

2)配送路线R(2)：0，4，5，7，2，0；

3)配送路线R(3)：0，0.

由于路线3未对任何客户服务，是多余的配送路线．在本研究提出的算法中，可行解在优化过程中若出现连续0的情况，则用单个0进行替代，从而改变了可行解编码长度并减少了车辆数．由于采用了可变长的编码方式，本算法在优化过程中可同时实现对车辆数和运输成本的优化．

2 快速多邻域迭代局部搜索算法

自从1986年Baum[13]提出迭代局部搜索算法(iteratedlocalsearch，ILS)以来，该算法已广泛用于求解组合优化问题．迭代局部搜索的主要思想是：从某个随机起始点出发，局部搜索和变异交替进行，在此过程中只保留最好的解．迭代局部搜索结构简单，易于找到问题的较好解，亦为本算法所用．图1给出FMNILS算法的伪代码．

图1 FMNILS算法的伪代码

Fig.1 Pseudo-code for FMNILS

2.1 构造初始解

在FMNILS算法中采用随机生成的方法来获得CVRP问题的初始解．假设CVRP问题中客户节点的集合为{1，2，…，N}，则初始解的生成可描述为

1)生成随机序列X=(x1，x2，…，xi，…，xN)，其中xi=1，2，…，N，且xi≠xj(i≠j)，并在序列X头部插入仓库节点0．

2)从节点x1开始向后寻找这样的节点xk，若满足配送路线(0，x1，x2,…，xk，0)为合法解(即满足所有约束条件)，配送路线(0，x1，x2,…，xk+1，0)为非法解，则在xk和xk+1之间插入仓库节点0，构造新的合法配送路线．再从xk+1开始按同样方法继续构造新的配送路线，直至所有分段路线均满足约束条件，并在末端插入仓库节点0．由此得到的新序列S即为VRP问题的初始解．

2.2 局部搜索算法

在求解VRP问题的局部搜索算法中，采用多种邻域结构有利于算法找到更好解．因此，本研究在局部算法中采用了4种常见的局部搜索算子(插入、交换、2-opt和2-opt*)，分别对应4种邻域结构．给定解S=(s1，s2，…，si，…，sM)和节点对si，sj(i≠j)，用si-1和sj-1表示si和sj在解S中的直接前驱节点，si+1和sj+1表示si和sj在解S中的直接后继节点，则以上4种局部搜索算子可描述为

1)插入(insert)：删除弧(si-1，si)、(si，si+1)和(sj，sj+1)，连接弧(si-1，si+1)、(sj，si)和(si，sj+1)．

2)交换(exchange)：删除弧(si-1，si)、(si，si+1)、(sj-1，sj)和(sj，sj+1)，连接弧(si-1，sj)、(sj，si+1)、(sj-1，si)和(si，sj+1)．

3)2-opt：删除弧(si，si+1)和(sj，sj+1)，添加弧(sj，si)和(si+1，sj+1)．

4)2-opt*：删除弧(si，si+1)和(sj，sj+1)，添加弧(si，sj+1)和(sj，si+1)，2-opt*只能在节点si和sj分属不同配送路线的条件下进行．

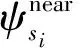
在局部搜索算法中邻域解的评估需要反复进行，因此，减小邻域解评估的计算复杂度能极大提高算法的运行效率．由于邻域解和当前解的差异较小，可通过计算两者的差异获得邻域解的适应值及合法性评估．为此，本研究将当前解中与车辆容量、最大行驶距离等约束条件相关的信息分解到各客户节点，依据客户节点的约束信息在4种常用的局部搜索算子(插入、交换、2-opt和2-opt*)中寻求邻域解合法性的快速评估方法．

2.2.1 客户节点的约束信息

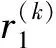
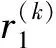
(2)

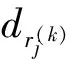
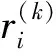
(3)

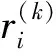
(4)

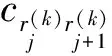
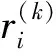
(5)

由此可知，客户节点约束信息的计算是一个累加过程，计算1条配送路线所有客户节点约束信息的计算复杂度为O(l)，这里l为该配送路线服务的客户数，每个客户节点约束信息的计算复杂度为O(1)．

2.2.2 邻域解的快速评估策略

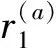
(6)

(7)

由此可得，解S′是否满足容量约束的判断条件为

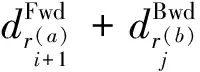
(2-opt*) (8)

其中，Q为车辆容量约束．

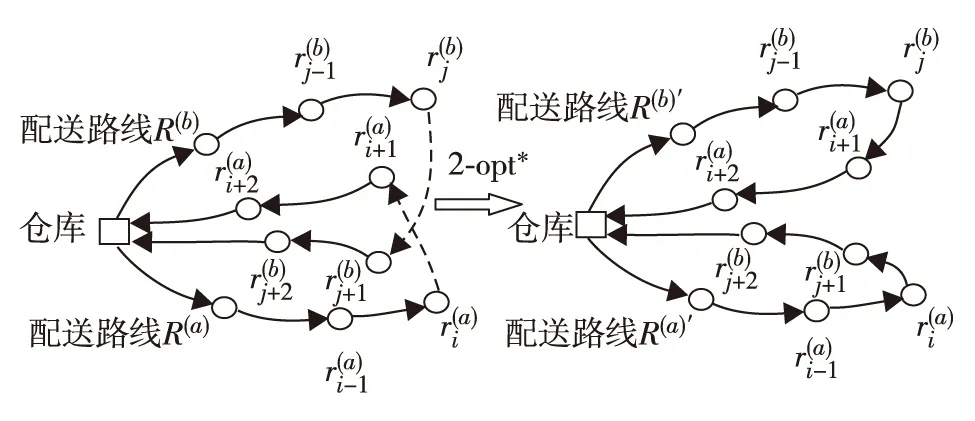
图2 2-opt*局部算子示意图Fig.2 Two-opt* local operator

类似可推导出其他3种局部算子所得邻域解是否满足容量约束的条件为

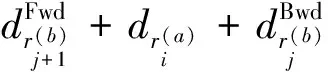
(insert) (9)

(exchange) (10)

(2-opt) (11)

同样可推导出4种局部算子所得近邻解是否满足最大行驶距离的判定条件为

(2-opt*) (12)

(insert) (13)

(exchange)(14)

(2-opt)(15)

在本算法执行过程中，只对合法解进行局部操作．合法解中的所有配送路线都满足容量约束和最大行驶距离约束．对于同一路线内的2个客户进行插入、交换和2-opt操作，并不改变配送路线内所服务的客户，改变的只是服务顺序.因此，该路线的配送货物总重量不发生改变，自然满足容量约束，无需进行容量约束判断；对于最大行驶距离约束，该路线的行驶距离变化和适应值的变化一致，在本节所述的局部搜索算法中只接受适应值得到改善的邻域解，即被接受的邻域解在该路线上的行驶距离较当前解更短，自然就满足最大行驶距离约束．而不被接受的邻域解是否满足最大行驶距离约束并不重要，所以也可以不进行最大行驶距离约束判断.

对CVRP和CDVRP的邻域解可通过计算适应值的差异来实现其适应值评估，其计算复杂度为O(1)．从式(8)至式(15)可见，各式的计算复杂度均为O(1)．因此，采用以上方法后，邻域解适应值评估的计算复杂度由O(N)降低为O(1)．

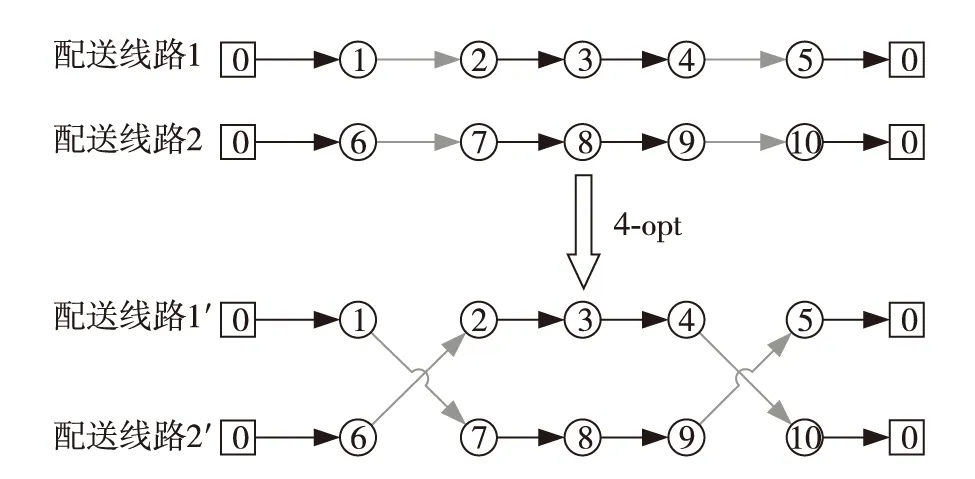
图3 4-opt局部算子示意图Fig.3 Four-opt local operator

客户节点约束信息的引入使得路径的配送需求和行驶距离可以快速获得，该信息可用于多种不同局部搜索算法所获邻域解的快速评估．除了本研究采用的4种局部搜索算子，客户节点的约束信息也可用于r-opt所获邻域解的快速地评估．例如对于图3的4-opt操作，对于邻域解中的新路线1′是否满足容量约束，只需要计算路径(0，1)、(7，8，9)和(5，0)的配送需求之和是否小于配送车辆的最大载重．路径(0，1)和(5，0)的配送需求分别为节点2的前载重和节点4的后载重，路径(7，8，9)的配送需求可以由节点10的前载重减去节点7的前载重获得．同样，可用相同的方法判断配送路线2′是否满足容量约束．当r取不同值时，也可以设计相应的合法性快速评估方法．对于最大行驶距离的约束，也可采用类似的方法．目前求解TSP问题的算法中许多是基于边交换(r-opt)操作的，由于邻域解合法性评估占用了大量的运算时间，使这些算法用于CVRP/CDVRP受到限制．因此，客户节点约束信息的引入使这些算法可方便地用于求解CVRP/CDVRP问题．

2.3 接受准则

在基本的ILS算法中采用最优接受准则，即只接受比当前解更好的解．此类接受准则容易使算法陷入局部最优，因此在求解CVRP问题的算法中常采用不同的接受准则．例如，IVND算法[3]采用类似模拟退火的接受准则；RTR算法[6]只接受对当前解的改变小于某一偏差的局部变换；FMNILS算法只接受适应值优于αf(S)的解，其中，α(α≥1)为接受因子，f(S)为当前解的适应值．FMNILS算法采用的接受准则，使当前解既有较大的机会跳出局部最优，又保证算法可集中在当前最优解附近区域进行搜索．

2.4 扰动

对VRP问题，由于约束条件的存在，设计相应扰动算法时需考虑所获解的合法性．通常是在扰动算法中加入约束条件，以保证所获解的合法性，或者设计相应的算法对扰动后的解进行合法化，以上方法都会增加算法设计的复杂度．由于FMNILS算法采用了可变长编码，车辆数在优化过程中可增可减．因此，在FMNILS算法中对扰动所获的非法解，只需在适当位置加入仓库节点(增加车辆数)就可实现解的合法化．

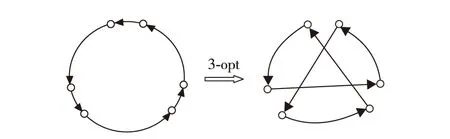
图4 3-opt扰动示意图Fig.4 Three-opt perturbation

在迭代局部搜索算法中采用的扰动方法对算法的求解精度和求解效率有较大影响．扰动范围不能太大，且需避免出现对当前解进行扰动、局部搜索后获得的解和当前解相同的情况[14]．本研究采用3-opt变换方法对当前解进行扰动，该方法对当前解的改变较小，且对扰动后的解进行插入、交换、2-opt和2-opt*这4种局部操作不易使其回到当前解．扰动方法为：首先随机选择3条边，然后进行如图4的3-opt变换．若变换后所得解不满足约束条件，则对不满足约束条件的配送路线在变换处增加1个仓库节点，使约束条件得以满足．

3 实验仿真及分析

本研究的实验平台为IntelE7500 2.93GHzCPU，操作系统为Windows7，编程语言采用C++．CVRP和CDVRP的测试问题采用Christofides等[15]提出的14个基准测试问题(记为C1～C14)和Golden等[16]提出的20个较大规模的测试问题(记为P1～P20)．在这2个测试集中，C1～C5、C11～C12和P8～P20为CVRP问题，其他的则是CDVRP问题．

为评估快速评估策略对局部搜索算法运行效率的影响，本研究使用FMNILS算法和未采用快速评估策略的多邻域迭代局部搜索算法(multi-neighborhoodILS，MNILS)求解不同规模的CVRP/CDVRP问题．实验中两个算法采用相同的参数和停止准则，其中设α=1.02； 若连续500代未能找到更好解，则算法停止．两个算法的差别仅在适应值的计算方法上，因此，在随机数发生器采用相同初始值的条件下，可保证两个算法能得到相同的解，所不同的是运行时间差异．实验结果如图5．

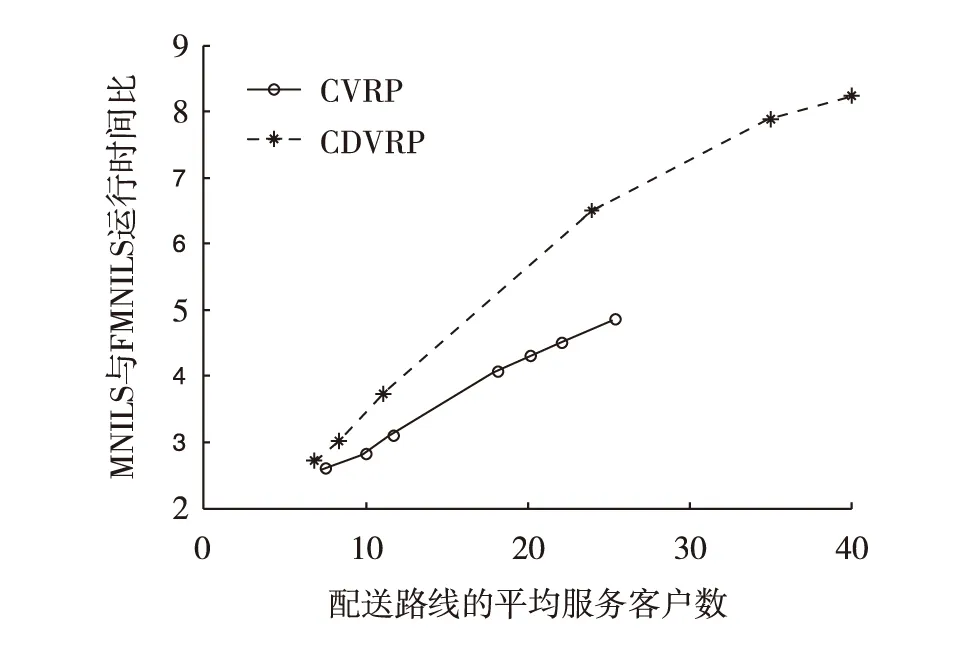
图5 FMNILS算法运行速度提高度与配送路线平均服务客户数的关系图Fig.5 Relationship between the average number of customers in a route and the improvement level of running speed by FMNILS

由图5可见，FMNILS在运行速度上的提高程度(以MNILS算法的平均运行时间和FMNILS算法平均运行时间的比值来衡量)，与配送路线的平均服务客户数大致服从线性关系．这是因为，MNILS算法中只对邻域解改变的路线进行合法性评估，其算法复杂度为O(l)，所以MNILS算法的运行时间和l相关，而l可近似等效为配送路线的平均服务客户数(即N/K)． 从图5可见，对于CDVRP问题，FMNILS算法用时更少，这是因为除了容量约束判断，在最大行驶距离约束判断上，FMNILS算法也节省了运算时间．

FMNILS算法整体性能的评估实验也是在Christofides和Golden测试集上进行的．实验设α=1.02； 若连续1 000代未能找到更好解，则算法停止．表1和表2给出FMNILS算法整体性能评估实验结果．

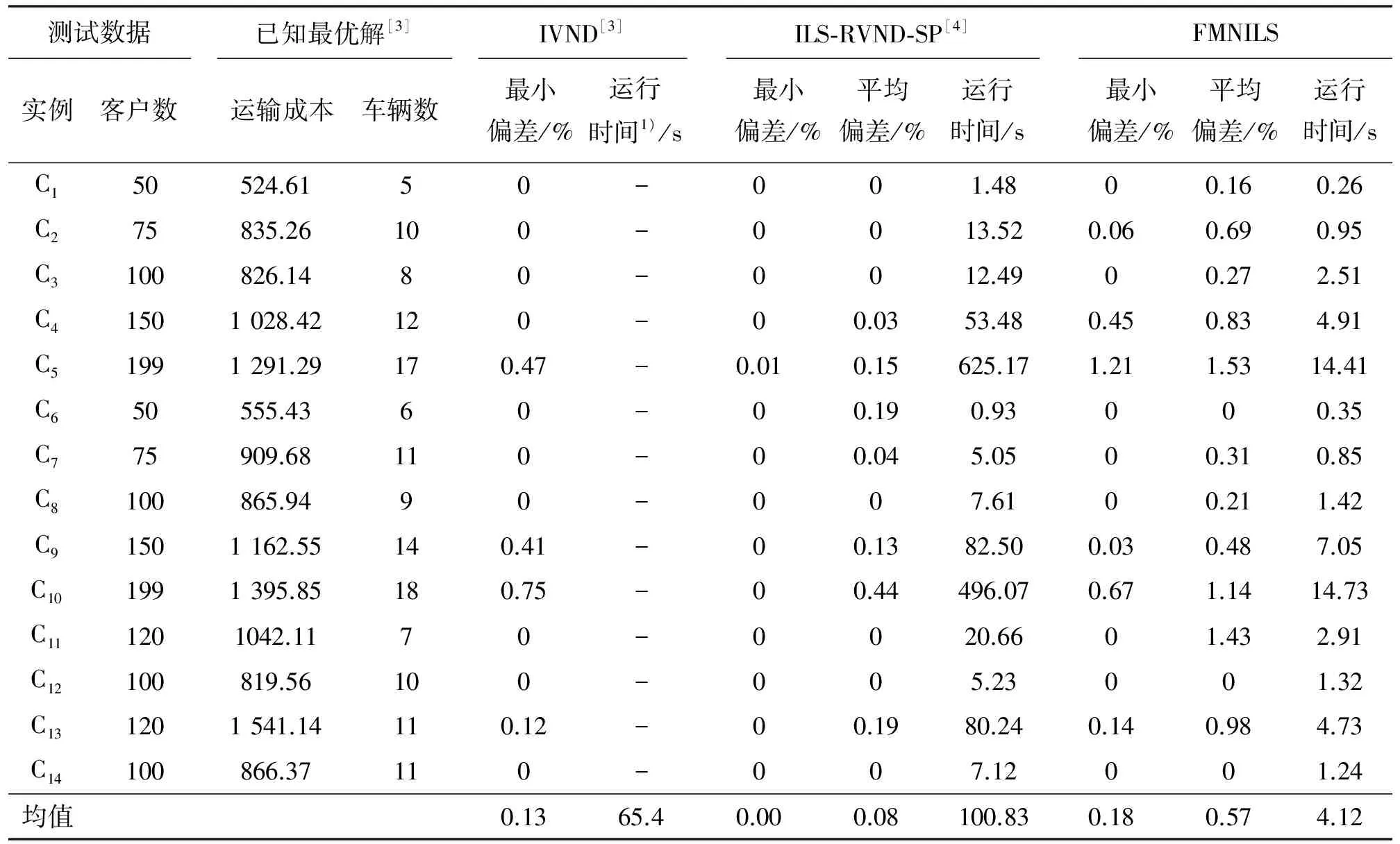
表1 Christofides测试集求解结果

1)文献[3]未给出平均偏差和单个实例平均运行时间的数据

在表1和表2中，已知最优解采用文献[3]的结果，最新结果可参考文献[4]；最小偏差和平均偏差分别为10次运行中的最好结果、平均结果与目前已知最优解之间的差异；运行时间为10次运行的平均时间．表1和表2还给出了另外2种基于ILS的算法(IVND[3]算法和ILS-RVND-SP[4]算法)求解CVRP问题的结果．IVND算法的实验平台是Pentium IV 2.93 GHz；ILS-RVND-SP算法的实验平台为Intel CoreTM i7 2.93 GHz.图6给出了4种不同算法在求解精度和时间上的比较(其中，FIVND是结合了本研究提出的快速评估策略的IVND算法)，图6(a)给出的是各算法求解单个问题的平均运行时间，为便于比较，图中给出各算法运行时间与FMNILS算法运行时间的比值；图6(b)给出各算法10次求解的最好结果与目前已知最优解的差异．从图6可见，FMNILS算法使用了远少于IVND算法的运行时间，但获得和IVND算法求解精度大致相当的结果(在Christofides测试集上FMNILS略差于IVND，在Golden测试集上FMNILS略优于IVND)；ILS-RVND-SP算法在ILS-RVND的基础上结合了集合划分的方法，其在两个测试集上的求解精度都优于FMNILS，然而其付出了更多的运算时间．从图6可知，结合了快速评估策略的FIVND算法在不影响求解精度的情况下，极大地减少了算法的运行时间．这说明快速评估策略可用于邻域解的评估，并不影响算法求解精度，因而它可以与基于邻域搜索的CVRP问题求解算法相结合，以期在获得相同精度解的情况下减少算法的运行时间．

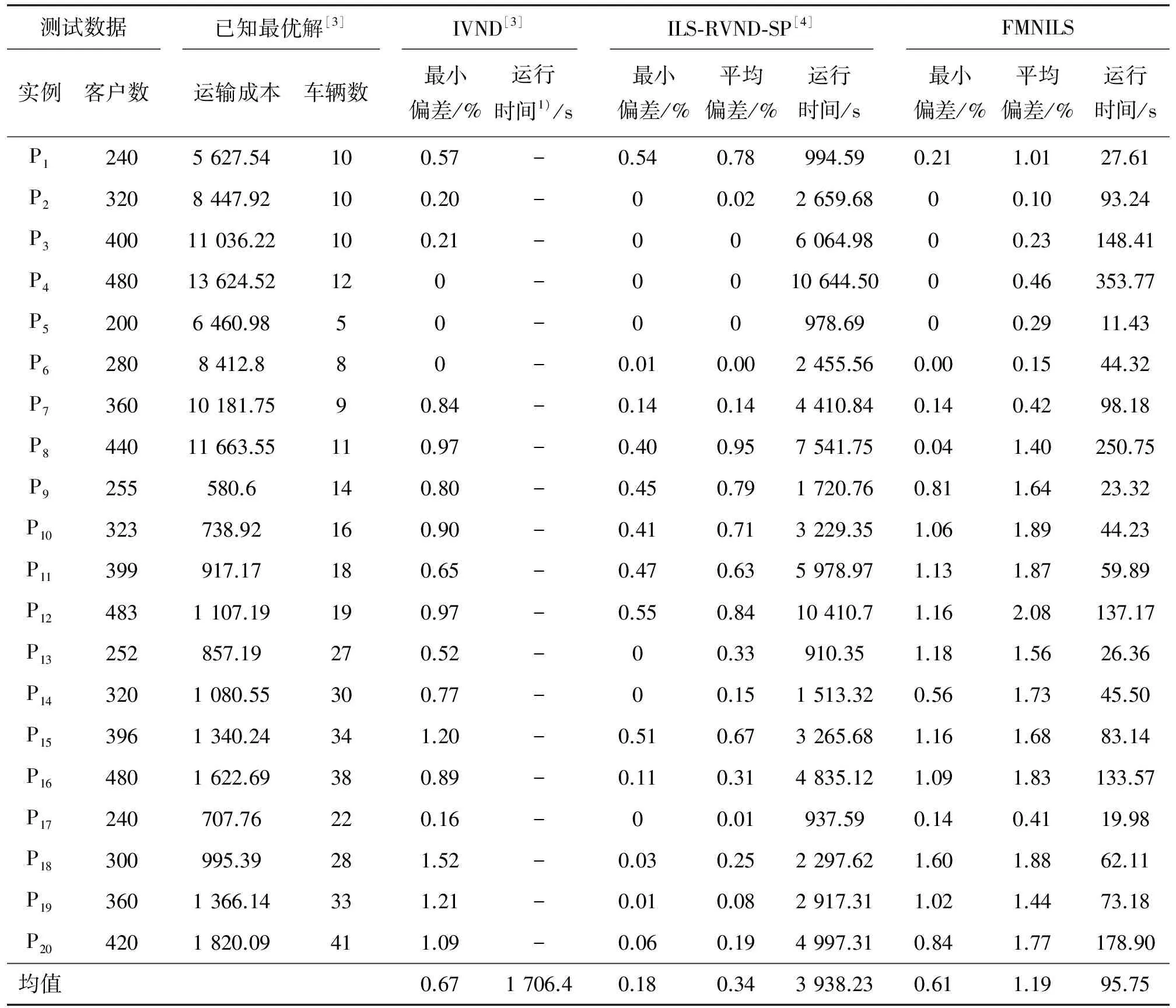
表2 Golden测试集求解结果

1)文献[3]未给出平均偏差和单个实例平均运行时间的数据

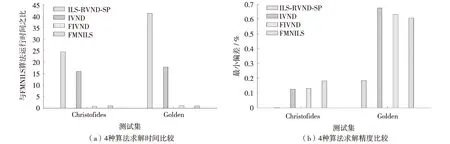
图6 FMNILS、IVND、FIVND和ILS-RVND-SP算法时间和求解精度比较Fig.6 Comparisons of rumming time and average deviation among FMNILS, FIVND, IVND and ILS-RVND-SP

结 语

VRP问题属于带有约束条件的组合优化问题，因而在局部搜索算法中对邻域解的评估不能直接通过当前解和邻域解的差异来实现．为此，本研究引入前载重、后载重、前向距离和后向距离的概念，提出一种邻域解合法性的快速评估策略．该策略实质上是将当前解与约束条件相关的信息分解到各客户节点，使邻域解的合法性评估可通过客户节点的约束信息来快速获得，避免了算法后续的局部搜索过程中对相关信息进行反复计算，大幅提高了局部搜索算法的运行效率．此外，本研究将采用了快速评估策略的局部搜索算子和迭代局部搜索算法相结合，设计应用于车辆路径问题的快速迭代局部搜索算法．实验仿真结果表明，该算法能够在较短时间内求得较大规模CVRP问题的满意解．

/ References：

[1] Laporte G，Toth P，Vigo D．Vehicle routing：historical perspective and recent contributions[J]．EURO Journal on Transportation and Logistics，2013，2(1/2)：1-4．

[2] Baldacci R，Mingozzi A，Roberti R．Recent exact algorithms for solving the vehicle routing problem under capacity and time window constraints[J]．European Journal of Operational Research，2012，218(1)：1-6．

[3] Chen Ping,Huang Houkuan,Dong Xieye.Iterated variable neighborhood descent algorithm for the capacitated vehicle routing problem[J]．Expert Systems with Applications, 2010，37(2)：1620-1627．

[4] Subramanian A，Uchoa E，Satoru Ochi L．A hybrid algorithm for a class of vehicle routing problems[J]．Computers & Operations Research，2013，40(10)：2519-2531．

[5] Subramanian A．Heuristic, exact and hybrid approaches for vehicle routing problems[D]．Niterói(Brazil)：Universidade Federal Fluminense，2012．

[6] Li Feiyue，Golden B，Wasil E．Very large-scale vehicle routing: new test problems, algorithms, and results[J]．Computers & Operations Research，2005，32(5)：1165-1179．

[7] Luo Jianping，Li Xia, Chen Minrong. Improved shuffled frog leaping algorithm for solving CVRP[J]．Journal of Electronics & Information Technology，2011，33(2)：429-434．(in Chinese) 骆剑平，李 霞，陈泯融．基于改进混合蛙跳算法的CVRP求解[J]. 电子与信息学报，2011，33(2)：429-434．

[8] Wink S，Back T，Emmerich M．A meta-genetic algorithm for solving the capacitated vehicle routing problem[C]// IEEE Congress on Evolutionary Computation(CEC). Brisbane(Australia)： IEEE Press，2012：1-8．

[9] Zachariadis E E，Kiranoudis C T．A strategy for reducing the computational complexity of local search-based methods for the vehicle routing problem[J]．Computers & Operations Research, 2010, 37(12)：2089-2105．

[10] ChrisGro⊇r C，Golden B，Wasil E．A parallel algorithm for the vehicle routing problem[J]．INFORMS Journal on Computing，2011，23(2)：315-330．

[11] Jin J，Crainic T G，Løkketangen A．A parallel multi-neighborhood cooperative tabu search for capacitated vehicle routing problems[J]．European Journal of Operational Research，2012，222(3)：441-451．

[12] Ishibuchi H，Yoshida T，Murata T．Balance between genetic search and local search in memetic algorithms for multiobjective permutation flowshop scheduling[J]．IEEE Transactions on Evolutionary Computation，2003，7(2)：204-223．

[13] Baum E B．Towards practical ‘neural’ computation for combinatorial optimization problems [C]// AIP Conference Proceedings 151 on Neural Networks for Computing．Snowbird Utah(USA)：AIP Publishing LLC，1986：53-58．

[14] Nguyen H D，Yoshihara I，Yamamori K，et al．Implementation of an effective hybrid GA for large-scale traveling salesman problems[J]．IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2007，37(1)：92-99．

[15] Christofides N，Eilon S．An algorithm for the vehicle-dispatching problem[J]．Operational Research Society，1969，20(3)：309-318．

[16] Crainic T G，Laporte G．Fleet management and logistics[M]．Berlin：Springer，1998．

【中文责编：英 子；英文责编：雨 辰】

A fast multi-neighborhood iterated local search algorithm for vehicle routing problem

Liu Wanfeng1, 2and Li Xia1, 2†

1)College of Information Engineering, Shenzhen University, Shenzhen 518060, P.R.China 2) Shenzhen Key Lab of Communication and Information Processing, Shenzhen 518060, P.R.China

For capacitated vehicle routing problems without/with maximum traveling distance constraint (CVRP/CDVRP), the evaluation of neighborhood solutions involves fitness calculation and feasibility assessment. This paper proposes a fast feasibility assessment strategy in which variable length coding is used to represent feasible solutions of vehicle routing problem. We introduce the concepts of pre-load, post-load, pre-distance and post-distance to obtain fast feasibility assessments for neighborhood solutions achieved by four widely used local search operations (insert, exchange, 2-opt, and 2-opt*). By combining the improved local search operations and iterated local search (ILS), we propose a fast multi-neighborhood iterated local search (FMNILS) for CVRP. The feasibility assessment strategy can reduce computational complexity of the neighborhood solution assessment fromO(N)toO(1).Experimentalresultsshowthattheimprovementinspeedisapproximatelylinearlyproportionaltotheaveragecustomernumberinaroute.ForCVRP/CDVRPproblemswith200—500customers,thealgorithmcangivesatisfactorysolutionswithanaveragedeviationoflessthan1.2%.Theaveragerunningtimeis96seconds,whichis6%ofthetimerequiredforthecounterpartalgorithms,orevenless.

artificial intelligence; heuristic algorithms; vehicle routing problem; multi-neighborhood; iterated local search; variable length coding

：Liu Wanfeng，Li Xia．A fast multi-neighborhood iterated local search algorithm for vehicle routing problem[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 196-204.(in Chinese)

TP

A

10.3724/SP.J.1249.2015.02196

国家自然科学基金资助项目( 61171124)，深圳市基础研究计划资助项目(JC201105170613A)

刘万峰(1974—)，男(汉族)，广东省兴宁市人，深圳大学博士研究生．E-mail：liuwf@163.com

Received：2014-06-11；Revised：2015-02-06；Accepted：2015-02-28

Foundation：National Natural Science Foundation of China (61171124); Shenzhen Key Project for Foundation Research (JC201105170613A)

† Corresponding author：Professor Li Xia. E-mail: lixia@szu.edu.cn

引 文：刘万峰，李 霞．车辆路径问题的快速多邻域迭代局部搜索算法[J]. 深圳大学学报理工版，2015，32(2)：196-204.