多跨简支梁桥加固措施的抗震性能评估

朱文正

广州大学土木工程学院，广州 510006

【土木建筑工程 / Architecture and Civil Engineering】

多跨简支梁桥加固措施的抗震性能评估

朱文正

广州大学土木工程学院，广州 510006

对一座典型的五跨简支铁路箱梁桥进行了多种工况的非线性地震反应分析，评价限位拉索、混凝土墩套、橡胶支座和铅芯橡胶支座等措施对桥梁主要构件抗震性能的影响.结果表明，各措施对桥梁构件的抗震性能有不同程度的改善，限位拉索和铅芯橡胶支座可以有效消减使用活动支座或普通橡胶支座时墩梁的相对位移；铅芯橡胶支座和普通橡胶支座均显著减少了桥墩的延性需求，但普通橡胶支座加大了墩梁间的相对位移和梁体对桥台的碰撞；限位拉索的初始间隙可考虑支座的允许变形，适当取较大值.建议采用铅芯橡胶支座或普通橡胶支座更换固定支座，必要时采用增加混凝土墩套的方法提高桥墩的塑性变形能力.研究成果可用于结构的易损性评价和基于桥梁整体性能的系统化抗震研究.

桥梁工程；抗震加固；多跨简支梁桥；限位拉索；普通橡胶支座；铅芯橡胶支座

简支梁桥是公路、铁路桥梁常用的桥梁型式，在强烈地震中容易遭到破坏，典型的破坏形式包括落梁、支座以及桥墩破坏等. 国内外许多学者通过模拟简支梁桥在强烈地震作用下的响应，研究主要构件的抗震性能. Dicleli等[1]认为支座刚度对多跨简支桥的地震响应影响显著，加之梁间碰撞的影响，容易产生落梁或支座的剪切破坏. 罗如登等[2]在多级抗震分析中对桥梁支座在水平静力约束方向上的弹簧刚度的取值进行了分析计算和对比研究，提出了支座的改进模型. Saiidi等[3]通过两跨和五跨简支梁桥限位拉索的研究，发现拉索可有效降低梁间相对位移，但是其减少量与拉索的数量不成比例. 杨风利等[4]考虑地震时车辆运行的安全性、土和基础的相互作用以及结构Rayleigh阻尼系数的变化对减隔震体系的影响，实现了铅芯橡胶支座设计参数的优化.黄艳等[5]采用非线性弹簧单元，模拟道床的纵向位移-阻力关系，分析轨道约束对铁路桥梁纵向抗震性能的影响. 目前，铁路简支梁桥的减震抗震计算多基于单墩模型，考虑整桥抗震性能的研究较少，考虑整桥性能分析加固措施影响程度的研究更少，本研究基于一座典型铁路简支箱梁桥，对其整体抗震性能进行多种减隔震加固措施的效果评价.

1 桥梁模型

1.1 桥梁概况

在某条铁路线上18座多跨铁路梁桥设计图纸综合分析的基础上，构建了1座5跨简支铁路箱梁桥.其中，跨径取标准跨径；为减小参数取值的不确定性导致中间跨与两侧桥台的地震响应相互影响，跨数的选取参考文献[6-7]关于建立全桥模型时考虑邻联结构和边界条件影响的要求；桥墩高度在取样桥梁的桥墩高度和水平刚度统计均值的基础上适当调整，使相邻桥跨的自振周期比接近2.0，以增加相邻跨的碰撞效应. 模型桥梁的跨径为32 m，梁重7 200 kN，二期荷载为200 kN/m，桥梁立面布置如图1. 伸缩缝宽度为3.0 cm. 桥墩采用2.5 m×6.4 m的圆端型截面，墩身纵向钢筋为176Φ25 mm，配筋率小于1%，箍筋配筋率约为0.16%. 桥墩基础采用10根直径为1.0 m的钻孔灌注桩. 每孔桥墩顶分别采用固定、纵向活动、横向活动以及多向活动等4类支座，梁体在纵桥向一端固定、一端活动. 场地类型为2类，设防烈度为8度.

图1 桥梁立面图(单位：cm)Fig.1 Elevation of bridge (unit in cm)

1.2 桥梁非线性单元

1.2.1 桥墩非线性模型

图2 桥墩Clough滞回模型Fig.2 Clough hysteresis model for piers

在剧烈地震作用下，桥墩可能进入塑性变形阶段，通过塑性变形耗散输入结构的地震能量，延长结构的自振周期，改变其地震反应特性. 在桥梁动力分析时，桥墩通常采用刚度退化的Clough模型，刚度退化系数β为0.2～0.6，如图2.其中，P1(+)和P1(-)分别为正负向的屈服强度；D1(+)和D1(-)分别为对应于正负向屈服强度的屈服变形. 蒋丽忠等[8]通过对铁路桥墩模型的低周反复荷载试验发现，低配筋率空心墩的滞回曲线的捏缩现象明显，耗能效果较差. 本算例桥墩的退化指数取0.4.

桥墩在纵横桥向的强度和延性参数见表1.约束混凝土和非约束混凝土的本构关系服从Mander模型[9]，钢筋服从双线性模型.

表1 桥墩截面强度与延性参数

1.2.2 轨道与梁体间相互作用

轨道对简支梁桥的纵桥向振动有较大约束.对于有碴桥梁，轨道与桥梁间的相互作用可由道床纵向位移-阻力(每延米纵向阻力)关系描述，以两者的相对位移u=2 mm为道床弹塑性转折点,一般可采用如图3的理想弹-塑性力学模型.道床最大纵向阻力与道床种类、断面尺寸及轨枕类型等因素有关,无载时道床最大纵向阻力在10～20 kN/m之间变化[5]，本研究取其纵向阻力为15 kN/m.

图3 道床纵向位移阻力关系Fig.3 Relationship between longitudinal deformation and resistance for track bed

1.2.3 梁间碰撞

梁间碰撞采用碰撞单元模拟. 文献[10]认为采用具有过大碰撞刚度的弹性单元会产生不切实际的碰撞力和加速度，可采用如图4的三折线弹性碰撞单元模拟梁间碰撞.其中，D0、D1和D2分别为梁间碰撞的初始间隙、2次间隙和3次间隙，K1、K2和K3分别为梁间碰撞的初始刚度、2次刚度和3次刚度，K2=K3/2，K1=K3/3.K3取梁体压缩刚度，以确保梁体在强烈地震作用下不开裂.计算得碰撞刚度K3=1.45×106kN/m.

图4 梁间碰撞模型[10]Fig.4 Pounding model between beems[10]

1.2.4 桥台刚度

桥台刚度是桥梁抗震计算的另一重要参数，但由于桥台在地震中破坏的实例较少见到，研究人员通常忽略其对结构抗震性能的影响.Eunsoo[11]通过对各国抗震规范的总结分析提出了桥台的非对称滑移三折线滞回模型，如图5.其中，F1a和F1p分别为桥台抗拉、抗压的第1屈服强度；F2a和F2p分别为桥台抗拉、抗压的第2屈服强度；Δ1a和Δ1p分别为桥台抗拉、抗压的第1屈服变形；Δ2a和Δ2p分别为桥台抗拉、抗压的第2屈服变形；K1a和K1p分别为桥台初始抗拉、抗压刚度；K2a和K2p分别为桥台抗拉、抗压的2次刚度；K3p为桥台抗压3次刚度.

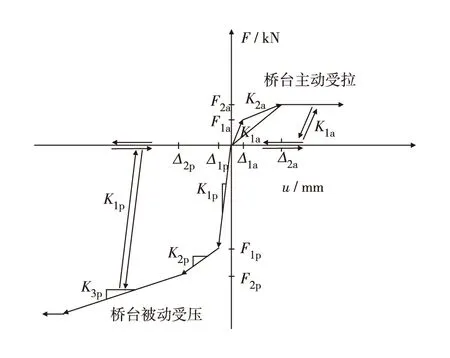
图5 被动与主动作用下桥台的分析模型[11]Fig.5 Analytical model of abutment in passive and active action[11]

Shamsabadi等[12]给出了台后不同填土情况下桥台的被动刚度和极限强度. 本研究选取粗砂作为桥台后填土，桥台的性能参数见表2.

表2 桥台性能参数表

1.2.5 地基刚度

桩-土-结构相互作用也会使结构的自振周期延长，改变其振动特性，因而在地震分析时需考虑地基刚度的影响[13]. 现行公路和铁路桥梁抗震设计规范规定桩基的刚度由“m”法计算，并且给出各种土质相应的“m”取值范围. 桩基水平刚度与桩的有效嵌固深度有关，有效嵌固深度约为桩径的5～10倍[8]. 为不失一般性，根据现行建筑抗震设计规范，取场地覆盖层为稍密的砾、粗和中砂[14]，“m”值为30～80MN/m4. 文献[15]认为“m”的取值在一定范围内变化对桥梁水平地震响应无显著影响，对于二类场地，“m”值可取50MN/m4. 计算得到桩基础刚度为：K1(竖向)=7.60×1010kN/m，K2(纵桥向)=1.62×109kN/m，K3(纵桥向转动)=9.86×109kN/m，K4(纵桥向)=1.94×109kN/m，K5(横桥向转动)=4.55×1010kN/m，K6(扭转)=1.46×1010kN/m.由于桩基破坏难以发现和修复，在桥梁抗震设计时不允许桩基中出现塑性铰，即基桩在地震作用下保持线弹性.

1.2.6 支座刚度

支座是连接桥梁上下部结构的传力构件，其水平刚度对桥梁结构的地震响应影响较大. 该桥采用竖向承载力为4 000kN的固定和活动支座. 文献[11]建议采用理想弹塑性杆单元和非线性弹簧单元模拟固定支座，采用理想弹塑性杆单元模拟活动支座，如图6. 其中，弹簧单元部分的Δ为初始间隙，k1、k2和k3分别为弹簧的初始刚度、1次刚度和卸载刚度；杆单元部分的K1、Kp分别为杆件屈服前后刚度，Fy为杆件屈服强度，杆单元部分的参数见表3.

图6 固定支座和活动支座的单元模型Fig.6 Elements for fixed and expansion bearings

表3 杆单元部分的支座参数

Table 3 Performance parameters of truss element for bearings

支座类型10-5K1/(kN·m-1)Kp/(kN·m-1)摩擦系数固定支座3．5600．37活动支座1．2300．20

2 抗震加固措施

桥梁抗震加固通常可以采用增加混凝土墩套、限位拉索及普通橡胶支座，或以铅芯橡胶支座取代固定支座等措施改善桥梁的地震响应，提高主要构件的抗震性能.

2.1 混凝土墩套

在剧烈地震中，桥墩塑性铰的转动能力对桥梁的安全具有非常重要的意义. 对于配筋率较低的桥墩，其抗弯和延性性能较差，在进行抗震加固时，可采用增加混凝土墩套的方法，即在墩柱周围附上一层钢筋混凝土以提高其抗弯、抗剪及延性变形能力. 一般情况下，圆柱或椭圆形柱可采用密排箍筋增加约束，其他形状的墩则可采用完整的外围箍筋，在混凝土墩身钻孔，并用连系钢筋连接. 混凝土墩套可以增加桥墩刚度约20%，增大允许转角50%以上. 动力分析结果表明，混凝土墩套对桥梁整体地震响应的影响不明显[16]，因而本研究在分析计算时未考虑增加混凝土墩套对桥墩参数的改变.

2.2 限位拉索

限位拉索可以安装在梁体与桥墩或桥台之间，限制梁体的移动，以防止在地震中落梁，弥补梁体搁置长度的不足. 在设计时限位拉索的强度可以大于或等于相应位置支座的支反力[17]. 通常采用钢绞线作为限位拉索，拉索长度为2.0 m，初始间隙s为20mm. 在地震反应分析时，采用如图7所示的双线性抗拉模型模拟拉索的力学性能，每根拉索的截面积约为25cm2.

图7 限位拉索的力学模型Fig.7 Mechanical model for restrainer cables

2.3 普通橡胶支座

普通橡胶支座可以延长桥梁的水平自振周期，避开地震卓越周期，从而有效提高桥梁的抗震性能. 一般而言，普通橡胶支座在延长结构自振周期的同时，也加大了地震中梁体的位移，增加了落梁的危险. 另外，竖向地震输入会减小梁体对支座的约束，降低摩擦力，导致梁体滑移，甚至落梁. 因而在采用普通橡胶支座时，可以使用限位拉索限制墩梁相对位移，防止落梁，特别是位于8度及以上场地的高墩大跨桥梁[14]. 选用的普通橡胶支座竖向承载力为4 000kN，橡胶厚度为60mm，取摩擦系数为0.25. 支座采用线性弹簧单元模型，刚度计算参考现行桥梁抗震规范[7].

2.4 铅芯橡胶支座

铅芯橡胶支座在房建和桥梁中已经使用了40多年，减震效果良好. 其基本原理是把结构的自振周期转移到地震卓越周期的范围之外，并增加结构阻尼，以减小上部结构的位移. 很多学者对其设计理论和计算方法进行了深入的研究.Turkington等[18]通过对铅芯尺寸、形状系数、支座厚度和屈服强度，以及桥墩、桥台和上部结构刚度等参数的研究，认为铅芯橡胶支座的减震作用随着结构特征周期或桥墩高度的增加而减小，可以用来调整桥梁墩台的地震力. 朱东生等[19]研究了隔震桥梁的初始周期、延性率和支座屈服前后刚度比等参数的隔震效果. 朱文正等[20]基于反应谱分析方法，通过等效线性化迭代计算对铅芯橡胶支座的初始刚度进行了优化. 杨风利等[4]进行了铁路简支梁桥减隔震支座设计参数的优化研究，提出采用改变支座屈服前后刚度比以满足减震需求. 周亚栋等[21]通过对影响桥梁隔震效果的2个显著因素(铅芯面积和桥墩高度)进行分析计算，提出评定桥梁减震效果的界限常数. 铅芯橡胶支座通常可以减少对桥墩和基础的抗震加固需求，其分析模型如图8.其中，K1和K2分别为铅芯支座屈服前后的刚度；Qy为支座的屈服强度. 在桥梁隔震设计中，应确保铅芯橡胶支座在多遇地震或者正常使用条件下不屈服. 取列车制动力为341.8kN，横向摇摆力为179.9kN，均小于多遇地震时桥梁的水平地震荷载，则每个支座的设计屈服力按多遇地震取为480kN，支座屈服后刚度一般取初始刚度的1/6.5，最大剪切变形取支座橡胶厚度的250%，计算得到隔震支座的初始刚度为3.23×104kN/m.

图8 隔震支座的计算特征值Fig.8 Characteristic value for LRB

3 加固桥梁地震性能评价

建立算例桥梁的非线性动力分析模型，如图9. 梁体采用空间弹性梁单元模型，梁体两端在纵桥向分别采用前文所述的固定、活动支座模型与桥墩连接，其他构件分别采用前文介绍的相关单元模型进行模拟. 通过10组地震波的动力时程分析，评价桥梁加固前后地震性能的改善程度. 结构阻尼采用Rayleigh阻尼，阻尼比ξ=0.05.

图9 桥梁的计算模型Fig.9 Calculation model of the bridge

3.1 地震波选取

动力计算选取的10组地震加速度见表4. 其中，前3组为相关文献在大量地震加速度记录综合评价的基础上建议的Ⅱ类场地的最不利地震波[22]；后7组为国内外结构抗震设计常用的Ⅱ类场地强震记录. 地震波幅值按8度罕遇地震调整，最大加速度峰值为400cm/s2.

表4 地震加速度时程

3.2 主要构件的地震响应

本研究主要考察桥梁纵桥向的地震响应，因而选择纵桥向为地震波主输入方向. 为比较各加固措施对桥梁不同构件的影响，本研究列举了El Centro波(以Array#10，N21E地震波为主输入地震波)作用下桥梁的非线性地震响应结果.

3.2.1 桥墩

图10和图11分别展示了几种工况下1#和3#桥墩的弯曲滞回曲线. 可以看出，设置铅芯橡胶支座时，1#桥墩的延性系数从2.75减少到0.93，普通橡胶支座可减少到1.25，而限位拉索只减少到2.44； 3#桥墩的延性系数从2.27减少到1.10，普通橡胶支座减少到1.50，限位拉索减少到1.83. 铅芯橡胶支座和普通橡胶支座都可以有效隔离桥梁上下部结构，大幅降低桥墩的延性需求；与其相比，限制墩梁相对位移的限位拉索对桥墩的延性需求较大.

图10 1#桥墩延性滞回曲线Fig.10 Ductile deformation response for pier 1#

图11 3#桥墩延性滞回曲线Fig.11 Ductile deformation response for pier 3#

3.2.2 活动支座

活动支座处的墩梁相对位移时程曲线如图12.其中，AB、RC、EB、ER和LB分别表示原桥、限位拉索、普通橡胶支座、普通橡胶支座+限位拉索及铅芯橡胶支座加固，他们的最大相对位移分别为(以2#桥墩为例)63.0、38.2、81.3、34.6和45.9 mm. 由图12可知，限位拉索和铅芯橡胶支座对改善墩梁相对位移的效果明显，把墩梁间最大相对位移从63.0 mm分别降低到38.2 mm和49.6 mm；而普通橡胶支座会导致墩梁相对位移显著增大，增加落梁的危险，可以同时采用限位拉索改善墩梁的相对位移. 图13为普通橡胶支座桥梁加入限位拉索后1#和3#桥墩的滞回曲线. 对比图10至图13可知，限位拉索对采用普通橡胶支座桥墩的延性需求增加不大(小于10%)，但有效改善了墩梁间相对位移，从81.3 mm减少到34.6 mm.

图12 2#墩活动支座的剪切变形时程Fig.12 Relative deformation response between piers 2# and girders with various retrofitting methods

图13 橡胶支座+限位拉索的桥墩延性滞回曲线Fig.13 Ductile deformation response for piers with EB and RC

3.2.3 固定支座

固定支座的纵桥向变形为22.8 mm，限位拉索对其影响不大，如图14.

图14 固定支座的水平变形时程Fig.14 Longitudinal deformation for fixed bearing

3.2.4 桥台

桥台的变形比较小，未进入屈服阶段. 但普通橡胶支座的使用增加了梁体与桥台碰撞的频率与力度，导致桥台的压缩变形从9.5 mm达到17.9 mm.

3.3 加固措施效果比较

10组地震波计算得到的主要构件的地震响应峰值(支座变形、桥台变形和桥墩延性需求等)可以更进一步说明各种措施的加固效果. 图15提供了桥梁主要构件在原桥和各种加固情况下地震响应峰值的对比，并通过构件响应的几个关键统计量表示计算结果的分布情况. 箱上下边缘分别表示构件地震反应峰值的第25和75分位值，箱状图上下方的粗线分别代表第5和95分位值，箱中间的粗黑线为中位值，白线则表示反应峰值的均值.

图15 桥梁主要构件计算结果对比Fig.15 Box plot of component for the retrofitted bridge

由图15可以看出，与原结构相比，限位拉索可以减少桥墩变形的平均峰值约16.5%，可以在简支桥梁中加入限位拉索以改善其抗震性能. 尽管在AB和RC两种工况下桥墩进入塑性变形阶段，但大部分计算结果处于允许延性变形范围内(模型试验得到轴压比为0.1的类似桥墩的平均允许延性系数约为4.2[8])，必要时可采用增加混凝土墩套的方法提高较矮桥墩的塑性变形能力. 另外，限位拉索可以限制墩梁相对位移，减小支座的剪切变形.

普通橡胶支座和铅芯橡胶支座均可以有效隔离桥梁的上下部结构，显著减小对桥墩的延性变形需求，取代易破坏的固定支座，是较好的加固措施. 铅芯橡胶支座对桥墩平均延性需求的降低较多，平均延性系数达到1.0左右，且计算结果分布的离散性较小，虽然其中位值已经达到屈服点，桥墩开裂，但这种破坏程度通常是可以接受的. 普通橡胶支座对桥墩的延性需求略大于铅芯橡胶支座，但会产生较大的支座变形，变形分布的离散性明显，且大部分已超过100%的支座剪切变形，文献[23]认为剪切变形r≤100%是可接受的普通橡胶支座剪切变形范围. 限位拉索可以降低普通橡胶支座的剪切变形50%以上，同时对桥墩的延性需求增加不大，可以用来控制橡胶支座的剪切变形.

固定支座的纵桥向变形基本处于30mm的水平，且受限位拉索的影响较小.该变形虽然不大，但是固定支座的原型试验[11]证明，变形超过20mm可能会导致支座断裂、倾覆和锚栓拔出等破坏.建议采用铅芯橡胶支座和普通橡胶支座进行更换，或采用限位拉索及防止梁体落座等措施确保支座破坏时桥面平顺和不落梁.

各工况下，桥台均未进入屈服阶段，和桥台在历次大地震中的表现一致. 但普通橡胶支座的使用增加了桥台的压缩变形和变形分布的离散性.

图16 改变拉索初始间隙的桥墩变形均值Fig.16 Longitudinal deformation for piers with EB and RC with different initial gaps

图17 改变拉索初始间隙的墩梁相对位移均值Fig.17 Relative deformation between girders and piers with EB and RC with different initial gaps

另外，为考察拉索初始间隙的影响，取初始间隙为10～60mm，计算得1#、3#桥墩的弯曲变形和墩梁相对位移均值分别如图16和图17.由图16和图17可知，拉索初始间隙从20mm变化到60mm时，1#桥墩的弯曲变形和墩梁相对位移均值分别改变了7.8mm和1.4mm，3#桥墩分别改变了5.9mm和1.6mm.初始间隙对较矮的1#桥墩的延性需求影响较大(降低约18%)，其他参数的影响均较小(小于7%)，故初始间隙可考虑支座的允许变形能力适当取较大值.

4 结 论

针对非抗震设计的多跨简支桥梁，通过非线性时程反应分析，评价限位拉索、普通橡胶支座、铅芯橡胶支座以及混凝土墩套对桥梁整体抗震性能的影响.研究表明，铅芯橡胶支座和普通橡胶支座均显著减少了桥墩的延性需求，是较好的抗震加固方法.但普通橡胶支座加大了墩梁间的相对位移和梁体对桥台碰撞的频率与力度，建议在抗震设计时采用限位拉索限制墩梁相对位移以减小落梁的危险.

限位拉索是一种简单易行的加固措施，可以有效消减使用活动支座或普通橡胶支座时墩梁的相对位移.除较矮桥墩的延性需求外，限位拉索初始间隙的变化对其他参数的影响不大，设置时可根据支座的允许变形能力适当取较大值.

除铅芯橡胶支座加固时桥墩的开裂程度较轻外，其他措施均会使桥墩产生较大的塑性变形，但大部分变形处于桥墩允许延性变形范围内，必要时可采用增加混凝土墩套的方法提高较矮桥墩的塑性变形能力.

固定支座在大震中存在破坏的危险，建议采用铅芯橡胶支座和普通橡胶支座进行更换或采用限位拉索和防止梁体落座等措施确保支座破坏时桥面平顺和不落梁.

本研究增加了对各种加固措施影响桥梁抗震性能程度的认识和了解.由于桥梁响应的系统特性，对构件抗震能力的改变可能危及桥梁整体的抗震性能，本研究在评价桥梁抗震性能时考虑了多种构件的抗震能力，为基于整桥易损性的系统化评价提供了量化标准.

/ References：

[1] Dicleli M, Bruneau M. Seismic performance of multispan simply supported slab-on-girder steel highway bridges[J]. Engineering Structures, 1995, 17(1):4-14.

[2] Luo Rudeng, Ye Meixin, Mo Chaoqing. The comparison study on valuing method of the stiffness on the direction of horizontal static constraint of support in seismic finite element analysis on bridges[J]. Journal of Railway Science and Engineering, 2008, 5(2):23-28.(in Chinese) 罗如登, 叶梅新, 莫朝庆. 桥梁支座水平静力约束方向抗震中的弹簧刚度取值方法对比研究[J]. 铁道科学与工程学报，2008, 5(2):23-28.

[3] Saiidi M, Randall M, Maragakis E A, et al. Seismic restrainer design methods for simply supported bridges[J]. Journal of Bridge Engineering, 2001, 6(5):307-315.

[4] Yang Fengli, Zhong Tieyi, Xia He. Study on optimization of the design parameter of seismic absorption and isolation bearing for railway simple supported beam bridges[J]. Journal of the China Railway Society, 2006, 28(3): 128-132.(in Chinese) 杨风利, 钟铁毅, 夏 禾. 铁路简支梁桥减隔震支座设计参数的优化研究[J].铁道学报,2006, 28(3): 128-32.

[5] Huang Yan, Yan Guiping, Liu Lin. Effects of rail restraints on longitudinal seismic response of railway bridges[J]. Journal of the China Railway Society, 2002, 24(5):124-128.(in Chinese) 黄 艳, 阎贵平, 刘 林. 轨道约束对铁路桥梁纵向地震反应特性的影响[J]. 铁道学报，2002, 24(5):124-128.

[6] James C, Phillip Y, John D O. Seismic retrofitting manual for highway structure[R]. FHWA-HRT-06-032. New York(USA): State University of New York, 2006.

[7] JTG/TB02—01—2008 Guidelines for seismic design of highway bridges[S].(in Chinese) JTG/TB02—01—2008公路桥梁抗震设计细则[S].

[8] Jiang Lizhong, Shao Guangqiang, Jiang Jingjing, et al. Experimental study on seismic performance of solid piers with rounded ended cross section in high-speed railway[J]. China Civil Engineering Journal, 2013,46(3): 86-95.(in Chinese) 蒋丽忠, 邵光强, 姜静静，等. 高速铁路圆端形实体桥墩抗震性能试验研究[J]. 土木工程学报, 2013,46(3): 86-95.

[9] Priestley M J N, Seible F. Seismic design and retrofit of bridges[M]. New York (USA): John Wiley & Sons Inc,1996.

[10] Zhu Wenzheng, Xu Zhonggen. Design method for seismic blocks of an isolation bridge[J]. Journal of Civil Engineering and Management, 2011, 28(3):407-411.(in Chinese) 朱文正, 徐忠根. 隔震桥梁横桥向挡块设计研究[J]. 土木工程与管理学报，2011, 28(3):407-411.

[11] Eunsoo C. Seismic analysis and retrofit of mid-America bridges[D]. Georgia (USA): Georgia Institute of Technology，2002.

[12] Shamsabadi A, Rollins K M, Kapuskar M. Nonlinear soil-abutment-bridge structure interaction for seismic performance-based design[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007,133(6):707-720.

[13] Ye Meixin, Tao Lu, Luo Rudeng, et al. Influence of pile- soil strueture interaction on anti-seismic performance of continuous bridge[J]. Science and Technology of West China, 2007(12):1-4.(in Chinese) 叶梅新，陶 路，罗如登. 桩-土结构相互作用对连续梁桥抗震性能的影响[J]. 中国西部科技,2007(12):1-4.

[14] GB 50011—2010 Code for seismic design of buildings[S].(in Chinese) GB 50011—2010 建筑抗震设计规范[S].

[15] Yang Fengli, Zhong Tieyi, Xia He. Study on variation effect of foundation elastic stiffness to seismic responses of railway simply supported beam bridge[J]. China Safety Science Journal, 2004, 14(11): 100-103.(in Chinese) 杨风利，钟铁毅，夏 禾. 基础弹性刚度对铁路简支梁桥地震响应的影响研究[J]. 中国安全科学学报，2004, 14(11): 100-103.

[16] Padgett J E, Reginald D. Three-dimensional nonlinear seismic performance evaluation of retrofit measures for typical steel girder bridges[J]. Engineering Structures, 2008, 30(10):1869-1878.

[17] Zhu Wenzheng, Liu Jianxin. Research on unseating prevention device for highway bridges[J]. Journal of Highway and Transportation Research and Development, 2009, 26(4):68-72.(in Chinese) 朱文正, 刘健新. 公路桥梁连梁装置研究[J]. 公路交通科技, 2009, 26(4):68-72.

[18] Turkington D H, Carr A J, Cooke N, et al. Seismic design of bridges on lead-rubber bearings[J]. Journal of Structural Engineering, 1989,115(12): 3000-3016.

[19] Zhu Dongsheng, Lao Yuanchang. Research on some design parameters of seismically isolated bridges[J]. China Civil Engineering Journal, 2000,33(5):53-56.(in Chinese) 朱东生,劳远昌. 隔震桥梁设计参数研究[J].土木工程学报,2000,33(5):53-56.

[20] Zhu Wenzheng, Liu Jianxin. Influence of lead rubber bearing on earthquake resisting behavior of bridges[J]. Journal of Chang’an University Natural Science Edition, 2004, 24(1):48-51.(in Chinese) 朱文正,刘健新. 铅销橡胶支座对桥梁抗震性能的影响[J]. 长安大学学报自然科学版,2004, 24(1): 48-51.

[21] Zhou Yadong, Zhu Wenzheng, Hu Zhaotong, et al. Evaluation method of aseismic effect of lead rubber bearing used in continuous beam bridge[J]. Journal of the China Railway Society, 2008, 30(8):59-64.(in Chinese) 周亚栋, 朱文正, 胡兆同，等. 连续梁桥铅销橡胶支座减震效果的评定方法[J]. 铁道学报，2008, 30(8):59-64.

[22] Liu Lin, Zhang Peng. Seismic evaluation of an existing rein- forced concrete bridge with tall piers[J]. Municipal Engineering Technology, 2005,23(s):108-116.(in Chinese) 刘 林, 张 鹏.一座既有混凝土高墩桥梁的抗震评估[J].市政技术, 2005,23(s):108-116.

[23] Mori A, Moss P J, Cooke N, et al. The behavior of bearings used for seismic isolation under shear and axial load[J]. Earthquake Spectra, 1999, 15(2):199-244.

【中文责编：坪 梓；英文责编：之 聿】

Seismic performance evaluation of retrofit measures for multi-span simple-supported bridges

Zhu Wenzheng†

School of Civil Engineering, Guangzhou University, Guangzhou 510006, P.R.China

This paper conducts a nonlinear time-history analysis of a typical 5-span simply supported bridge by using three-dimensional models to evaluate the effectiveness of various retrofit measures. Restrainer cables, concrete jackets, elastomeric bearings, and lead rubber bearings are assessed for their influence on the variability of critical components in the bridge. The results indicate that each retrofit measure may be effective for components of the bridge in different degrees. The restrainer cables and lead-rubber bearings (LRBs) are effective in controlling the relative deformation between girders and piers; LRBs and elastomeric bearings improve the response of the vulnerable columns, elastomeric bearings lead to increased abutment demands, and a larger value can be chosen for the initial gap of the restrainer cable based on the permitted deformations of the bearings. Additionally, it is recommended to replace these fixed bearings with elastomeric bearings or LRBs, and to enhance ductility capacity of the columns with concrete jackets when necessary. The results can be used for vulnerability assessments that consider the impact of retrofit on system vulnerability reflecting the contribution of multiple components.

bridge engineering; seismic retrofit; multi-span simple-supported bridge; restrainer cables; elastomeric bearing; lead rubber bearing

：Zhu Wenzheng. Seismic performance evaluation of retrofit measures for multi-span simple-supported bridges[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 152-161.(in Chinese)

TU 392.303

A

10.3724/SP.J.1249.2015.02152

广东省科技计划资助项目(2011A030200019)

朱文正(1971—)，男(汉族)，河南省上蔡县人，广州大学副教授、博士.E-mail:zhu7101@163.com

Received：2014-07-03；Revised：2014-12-29；Accepted：2015-01-31

Foundation：Science and Technology Project of Guangdong Province(2011A030200019)

† Corresponding author：Associate professor Zhu Wenzheng. E-mail: zhu7101@163.com

引 文：朱文正. 多跨简支梁桥加固措施的抗震性能评估[J]. 深圳大学学报理工版，2015，32(2)：152-161.