盾构隧道同步注浆的压力分布及其影响因素

邱明明，杨果林，姜安龙

1)中南大学土木工程学院，长沙 410075；2)厦门轨道交通集团有限公司，福建厦门 361001

【土木建筑工程 / Architecture and Civil Engineering】

盾构隧道同步注浆的压力分布及其影响因素

邱明明1，杨果林1，姜安龙2

1)中南大学土木工程学院，长沙 410075；2)厦门轨道交通集团有限公司，福建厦门 361001

结合城市地铁盾构法隧道工程实际，以盾尾同步注浆浆液环向填充过程为研究对象，选取环向任意一点建立注浆压力力学模型.假设浆液符合宾汉姆流体，应用流体力学与极限平衡法的基本原理，推导盾构壁后同步注浆环向填充压力分布统一计算模型，并将此模型推广到多孔注浆情形. 工程实例分析表明，推导的盾构同步注浆压力分布统一模型合理；小径盾构隧道宜采用四孔注浆，大径盾构隧道宜采用六孔或多孔注浆方式；注浆孔位置、盾尾间隙和截面流量对浆液压力分布有重要影响，应在盾构施工中予以重视.

隧道工程；盾构施工；同步注浆；盾尾间隙；压力分布；地铁建设

地铁建设已成为现代城市建设的重要组成部分，地铁建设事业的高速发展也给地下工程施工带来了广阔的应用空间和严峻的挑战. 在城市工程建设中，周围环境对城市施工提出了越来越高的要求，而盾构法施工不可避免地会对周围环境产生扰动和影响，造成地表沉降、周边建筑物倾斜和地下管线断裂等工程问题[1-4]. 隧道壁后注浆对盾构掘进引起的地表沉降的影响不容忽视，同时注浆压力也是隧道衬砌结构上的一种重要荷载[5-13]，对衬砌管片的受力与变形有重要影响. 因此，研究盾构壁后同步注浆填充机理及注浆压力分布模式，对衬砌结构设计和控制地层稳定有重要指导意义.

针对盾构壁后注浆压力问题，诸多学者进行研究，并取得了一系列成果. Koyama[14]通过模型试验指出，注浆压力过大会破坏密实砂层局部土体，使土压力分布不均；注浆压力过小又会使浆液不能完全充填空隙，造成土压力分布不均. Kasper等[15]通过对盾尾注浆进行数值模拟分析得出，浆液注入盾尾空隙后的浆体压力分布形式对地层变形和管片受力具有决定性作用. 国际隧道协会推荐注浆荷载分布模式为三角形分布[16]. 朱合华等[17-19]通过对盾构典型施工阶段、注浆材料硬化过程和注浆压力分布等因素进行模拟，假设注浆压力以注浆孔为对称中心呈等腰三角形分布，探讨了施工过程对衬砌结构受力的影响. 叶飞等[20-21]基于浆液柱面扩散理论，假定注浆浆液为牛顿流体，推导了盾尾注浆和管片注浆2种情况下的浆液扩散半径及对管片产生的压力计算式. 袁小会等[22]采用宾汉姆流体模型，推导了浆液注入盾尾空隙后考虑浆液扩散距离和注浆时间相关的浆体压力分布计算模型. 白云等[23-24]采用牛顿流体模型，推导了四孔注浆盾构隧道注浆压力分布计算模型. 邱明明等[25]分别采用牛顿流体及宾汉姆流体模型，对四孔注浆盾构隧道注浆压力分布进行了对比分析.

综上所述，现有的研究成果大多是基于小直径四孔注浆模式推导的计算模型，对大直径多孔注浆压力分布模式研究相对较少. 因此，本研究在借鉴已有研究成果的基础之上，考虑盾构直径的影响，假设注浆浆液符合宾汉姆流体，应用流体力学与极限平衡法的基本原理，对四孔及六孔注浆模式下浆液环向填充压力的大小及分布模式进行理论推导，得出同步注浆压力环向分布统一计算模型，并通过工程实例分析，讨论了注浆孔位置、盾尾间隙和截面流量对浆液压力分布的影响.

1 流体模型

根据流体的流变特性，可将流体流型分为牛顿流体、宾汉姆流体和幂律流体[26]. 浆液流变特性试验表明[11]，硬性浆液的流变特性符合宾汉姆流体特征，且塑性黏度取值范围为1～4 Pa·s，剪切应力取值范围为10～40 Pa.

宾汉姆流体，也称黏塑性流体，不仅其黏性影响流动，且流体只有克服自身的剪切屈服强度才能发生流动. 假设宾汉姆流体的速度分布如图1，其方程式为

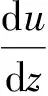
(1)

其中，τ为剪切应力，单位为Pa；τ0为浆体临界剪切应力，单位为Pa；μ为流体动力黏性系数，单位为Pa·s；du/dz为剪切变形速率，单位为s-1；u为浆液流速，单位为m/s. 图1中，zb为宾汉姆流体流核半高度，单位为m；z0为盾尾间隙半厚，单位为m.

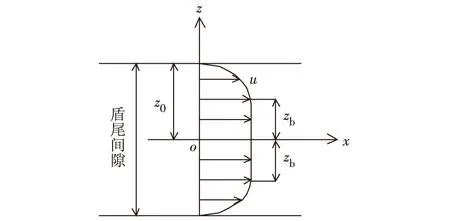
图1 宾汉姆流体速度分布图Fig.1 Speed distribution of Bingham fluid

2 同步注浆压力分布计算模型

2.1 浆液在盾尾间隙中的充填机理

盾构掘进过程中，在衬砌管片背面与隧道毛洞壁之间会形成一环形空隙，使围岩(土)暂时处于无支护状态，该空隙即为盾尾间隙. 理论上，单位时间内形成的盾尾间隙体积Vt为[2]

(2)

其中，K为浆液注入率，一般取150%～200%；D为盾构机外径，单位为m；d为盾构管片外径，单位为m；L为单位时间掘进长度，单位为m；δ为盾尾间隙厚度，单位为m，一般取值范围为0.08～0.16m；vd为盾构掘进速度，单位为m/s；t为掘进时间，单位为s.

盾构施工时，根据盾构直径的大小设置不同数量的注浆孔，一般小径隧道多采用四孔注浆，大径隧道多采用六孔或八孔注浆，如图2.浆液通过注浆孔注入盾尾间隙，然后逐渐填充整个间隙空间，其填充过程是一个复杂的空间动态的过程. 为简化计算，将浆液压力在盾尾间隙的形成与消散分成2个相对独立的阶段：第1阶段为浆液压力的形成，主要沿隧道横断面充填；第2阶段为浆液压力的消散，主要沿隧道纵断面挤压充填.本研究重点分析浆液在盾尾间隙沿隧道横断面的形成过程中所产生的压力分布模式.

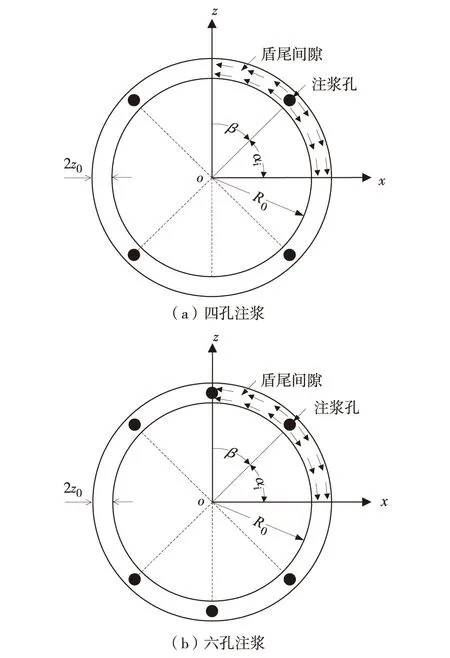
图2 浆液沿隧道环向充填过程Fig.2 Circumferential filling process of grout in shield tail interspace

2.2 基本假设

1)浆液为均质、不可压缩、各向同性的稳定流体；

2)注浆过程中，浆液始终符合宾汉姆流体特性；

3)各注浆孔注浆量一定，且沿环向均匀扩散；

4)管片-浆液-地层之间接触面光滑；

5)不考虑浆液与地层中水的相互渗透作用；

6)只考虑浆液沿隧道径向的速度变化，浆液速度损失不计.

2.3 理论推导

圆形隧道为轴对称图形，注浆孔分布左右对称，因此可认为两侧对称注浆孔压力一致，即注浆压力分布沿隧道竖轴对称分布. 由图2可知，浆液从注浆孔注入后，沿环向分为向上和向下2种流动情况，因此，需对这2种力学模式分别讨论.

当浆液从注浆孔向上注浆时，浆体流动受力简图如图3.

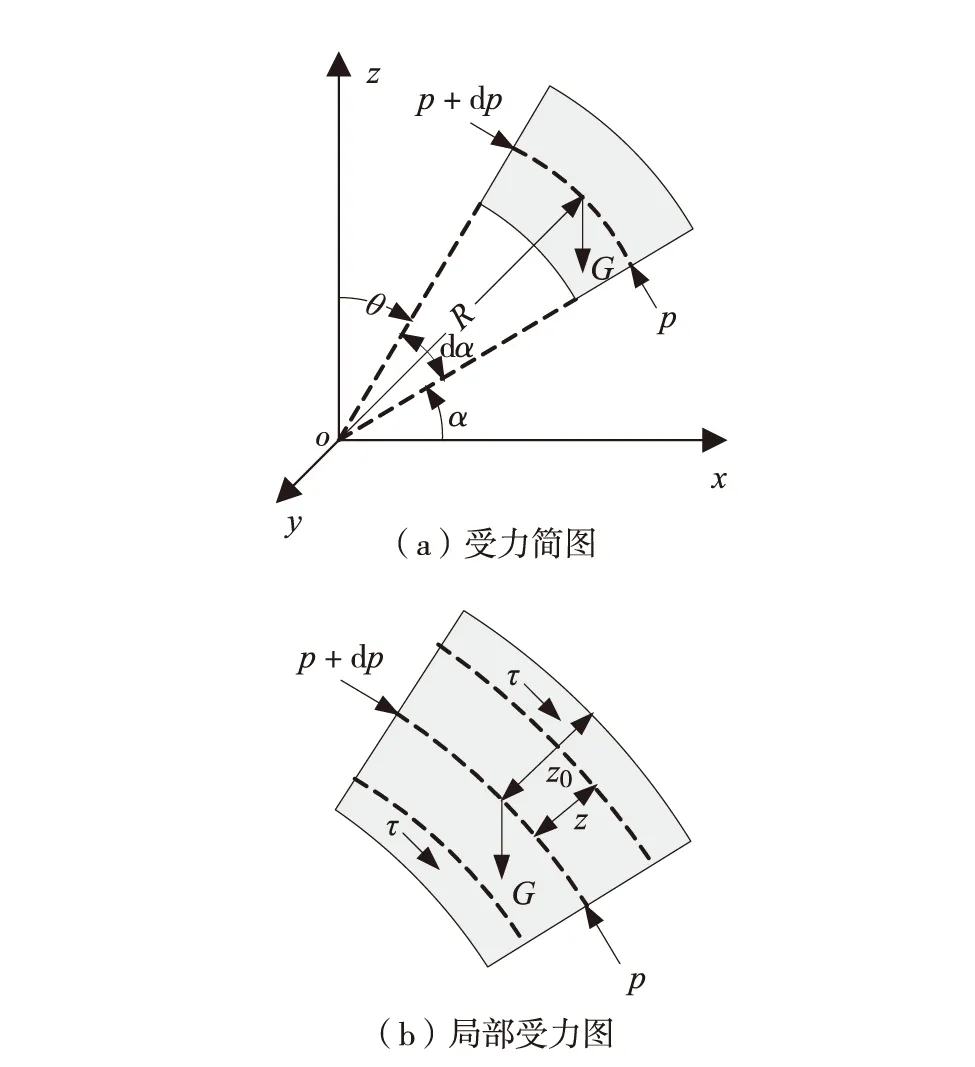
图3 浆体向上流动受力简图Fig.3 Mechanical diagram of upward flow of grouting

根据流体受力平衡，将各作用力向流线中心线方向投影，可得

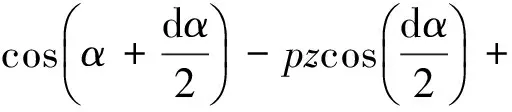
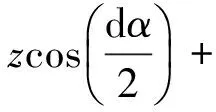
(3)

其中，p为浆体压力，单位为Pa；R为隧道计算半径，单位为m；τ为浆体剪应力，单位为Pa；z为沿隧道径向流体高度，单位为m；ρ为浆液饱和密度，单位为kg/m3；g为重力加速度，单位为m/s2；α为隧道半径与x轴间的夹角；θ为隧道半径与z轴间的夹角;G为浆体所受重力.

设sin(dα/2)≈0，cos(dα/2)≈1，并略去高阶微量，可得

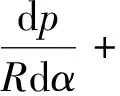
(4)

宾汉姆流体流动过程中存在流核. 设流核高度为2zb，则当z=zb时，浆液停止流动，流核截面内流体速率du/dz=0，流核边缘浆液的剪切应力最小，流速最大；从流核边缘到浆液与土体及管片界面的截面上的剪切应力最大，流速为0.

由式(1)和式(4)可得，宾汉姆流体流核半高度zb为

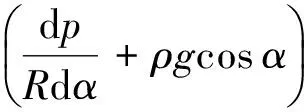
(5)

综合式(1)、式(4)和式(5)，可得注浆浆液流速沿z方向的分布为

根据式(2)和式(6)，可得单位时间内截面的平均流量为

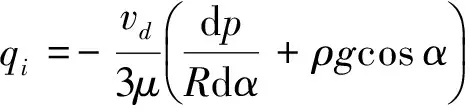
(7)

将式(7)分离变量可得

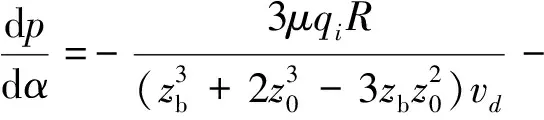
(8)

由边界条件α=α1，p=pi，有

ρgR(sinα1-sinα),α1≤α≤α2

(9)

其中，α1为第i个注浆孔向上注浆范围，α2为第i个注浆孔向下注浆范围. 将式(9)的α用θ(β1≤θ≤β)替换，且α=π/2-θ，α1=π/2-β，可得从注浆孔向上注浆时，注浆压力分布为

ρgR(cosβ-cosθ),β1≤θ≤β

(10)

其中，pi为第i个注浆孔注浆压力，单位为Pa；qi为第i个注浆孔向上注浆截面平均流量，单位为m3/s；zb为流体流核半高度，单位为m；z0为盾尾间隙半厚度，单位为m；β为第i个注浆孔与z轴间的夹角；β1为第i个注浆孔向上注浆范围.

当浆液从注浆孔向下注浆时，浆体流动受力简图如图4.

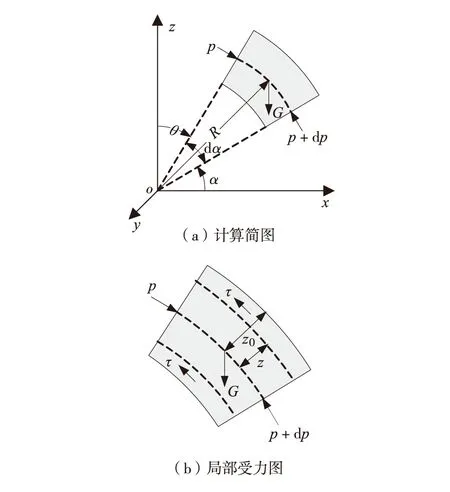
图4 浆体向下流动受力计算简图Fig.4 Mechanical diagram of downward flow of grouting

同理，当浆液从注浆孔向下注浆时，注浆压力分布为

ρgR(cosβ-cosθ),β≤θ≤β2

(11)

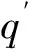
综上，根据式(10)和式(11)，可得盾构隧道多孔注浆情况下，注浆压力分布统一计算模型为

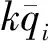
(12)

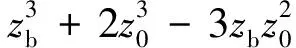
故由式(12)可得在四孔和六孔注浆情形下的注浆压力分布，见表1.

表1 同步注浆压力分布计算模型

3 工程实例分析

3.1 工程概况

[27]提供的Sophia盾构隧道工程概况及注浆参数，注浆计算参数见表2. 选取3种注浆方案对盾构壁后同步注浆压力分布进行对比分析：

方案1：盾构机外径D=6.52 m，管片外径d=6.2 m，盾尾间隙厚度δ=0.16 m，采用四孔注浆，注浆孔布设见表3.

表2 盾构同步注浆主要计算参数[27]

表3 四孔注浆布设及注浆压力

方案2：盾构机外径D=9.77 m，管片外径d=9.45 m，盾尾间隙厚度δ=0.16 m，注浆方案同方案1.

方案3：盾构机外径D=9.77 m，管片外径d=9.45 m，盾尾间隙厚度δ=0.16 m，采用六孔注浆(Sophia隧道实际注浆模式)，注浆孔布设见表4.

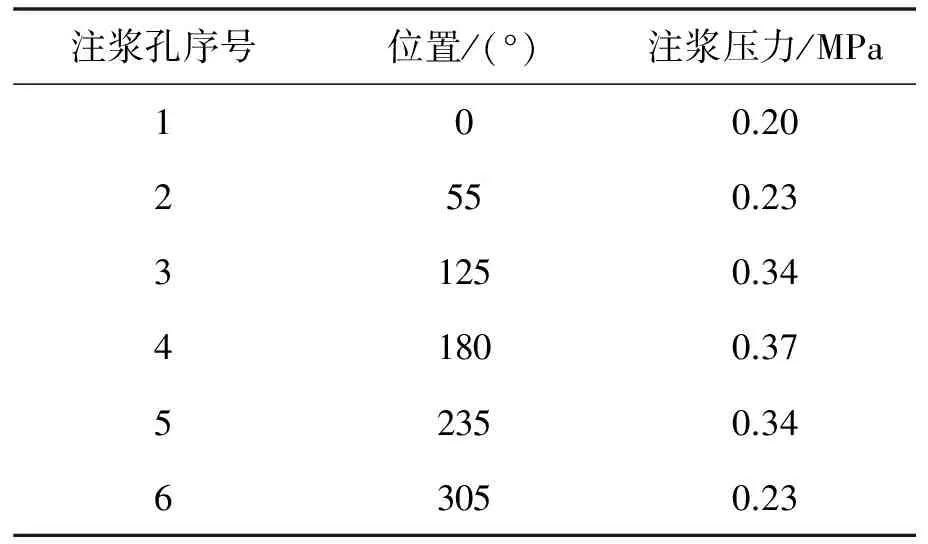
表4 六孔注浆布设及注浆压力

3.2 注浆压力分布计算结果

设各注浆孔向上、向下充填的截面流量q相等，且由同步注浆的注入总量决定. 隧道壁后同步注浆左右对称，取一半进行计算，注浆注入率K取150%，故由式(2)可得不同孔数及隧道半径的平均流量分别为

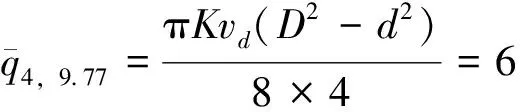
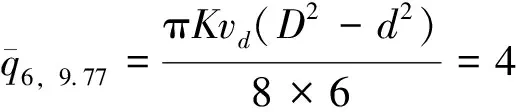
根据四孔及六孔注浆浆液压力分布模式，将上述3种方案注浆参数分别代入计算式，注浆压力理论计算结果与实测值对比见表5及图5. 由表5和图5可得，采用本研究推导的注浆压力分布模型得到的计算结果与Sophia隧道注浆浆液压力实测值吻合较好，证明本研究推导的注浆压力分布模型合理可行.由图5可知，注浆浆液压力从拱顶至拱底呈非线性分布；当D=6.52 m时，采用四孔注浆方式，拱顶、拱腰和拱底浆液压力分别为0.200、0.760和0.351 MPa；当D=9.77 m时，采用四孔和六孔注浆方式，拱顶浆液压力分别为0.178和0.200 MPa，拱腰浆液压力分别为0.264和0.279 MPa，拱底浆液压力分别为0.350和0.370 MPa. 由图5可明显看出，小径隧道采用四孔注浆，浆液压力分布比较均匀；大径隧道采用四孔注浆在拱顶及拱顶浆液压力均偏小，采用六孔注浆后浆液压力分布较均匀. 故对大径盾构隧道采用四孔注浆方式，会导致注浆浆液压力分布不均或压力不足情况，而影响浆液在盾尾间隙的填充速率、填充程度及浆液压力分布形式，最终造成盾尾壁后注浆效果不良. 因此，对于大径盾构隧道，建议采用六孔或更多孔注浆方式.

表5 同步注浆压力分布计算结果

图5 浆液压力计算值与实测值对比Fig.5 (Color online) Comparison between calculated and measured values

3.3 影响因素分析

根据式(12)可知，影响浆液压力分布的因素较多，主要可归结为3方面：

1)浆液参数，包括浆液密度、黏度系数和静剪切力；

2)注浆施工参数，包括注浆压力、截面流量(注浆量或注入率)、注浆孔数量和注浆孔位置；

3)盾构施工参数，包括隧道直径、盾尾间隙、掘进速度.

基于上述讨论，以六孔注浆为例，重点研究注浆孔位置、盾尾间隙和截面流量对浆液压力分布的影响规律.

3.3.1 注浆孔位置的影响

保持其他注浆计算参数不变，注浆孔位置按表6取值，分别研究不同注浆孔位置对浆液压力分布的影响，计算结果及曲线分别见图6和表7.

由图6可得，在0°～90°范围，方案1浆液压力曲线在外侧，方案3浆液压力曲线在内侧，由此说明注浆孔越靠近拱顶位置，注浆压力越大； 在 90°～180°范围，方案3浆液压力曲线在外侧，方案1浆液压力曲线在内侧，由此说明注浆孔越靠近拱底位置，注浆压力越小.

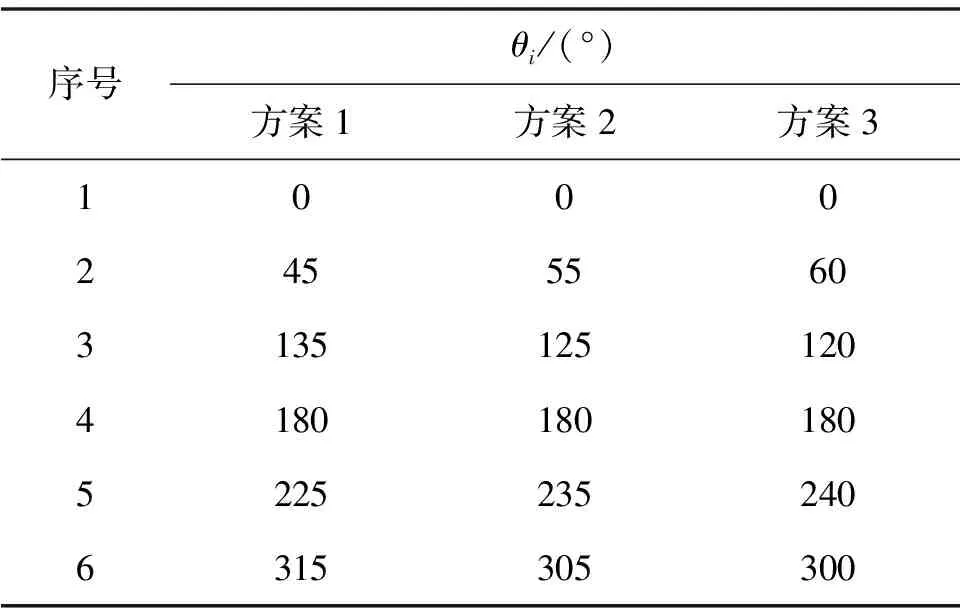
表6 注浆孔位置

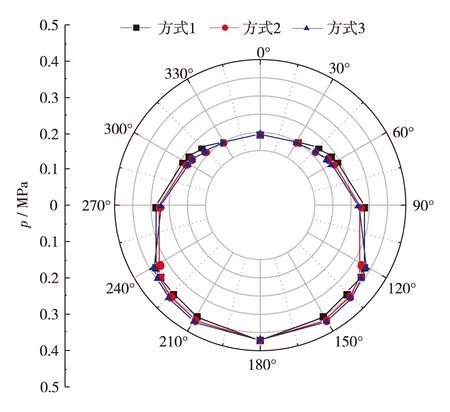
图6 不同注浆孔位置的浆液压力分布对比Fig.6 (Color online) Grouting pressure distribution under different grouting holes positions

表7 注浆孔位置对浆液压力分布的影响

Table 7 Impact of grouting hole positions on grouting pressure distribution 单位：MPa

方案0°30°45°55°60°90°120°125°135°150°180°10．2000．2080．2300．2410．2470．2900．3330．3390．3400．3520．37020．2000．2040．2160．2300．2360．2790．3220．3400．3510．3630．37030．2000．2040．2160．2270．2300．2750．3400．3460．3570．3690．370

3.3.2 盾尾间隙的影响

在实际盾构掘进施工过程中，超挖、纠偏及转弯等情况均会导致实际盾尾间隙厚度明显大于理论值，因此，在软土地区盾构掘进中实际注浆量一般为理论值的150%～200%，甚至更高. 为研究盾尾间隙厚度对注浆压力分布的影响，取盾尾间隙厚度S分别为0.10、0.16和0.20m进行计算，结果见表8和图7.

表8 盾尾间隙对浆液压力分布的影响

由图7可得，在45°位置，三者对应的浆液压力分别为0.195、0.216和0.222 MPa；在120°位置，三者对应的浆液压力分别为0.291、0.322和0.330 MPa；三者所对应的浆液压力分布曲线关系依次从内向外. 由此说明，盾尾间隙越大，浆液压力越大.故在盾构设计及施工中，应合理控制盾尾间隙厚度，以减小注浆量及浆液压力引起的地层变形.

3.3.3 截面流量的影响

在注浆过程中，考虑到注浆截面流量对注浆压力分布的影响，分别取注浆截面流量为 0.004 35、0.005 22和0.005 80 m3/s进行计算，结果见图8和表9.

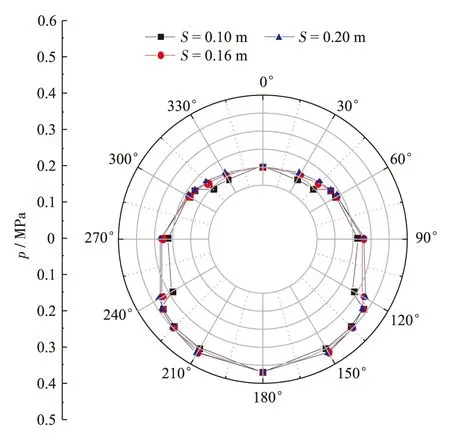
图7 不同盾尾间隙的浆液压力分布对比Fig.7 (Color online) Grouting pressure distribution under different shield tail interspaces

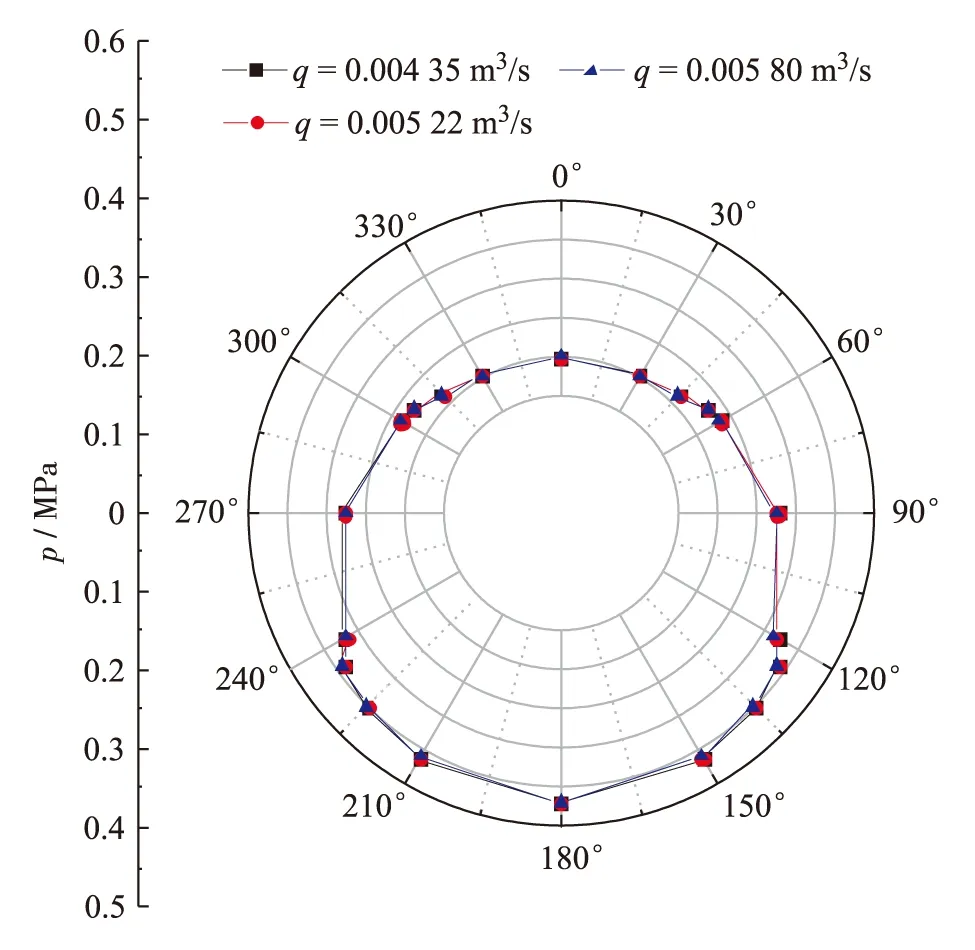
图8 不同截面流量的浆液压力分布对比Fig.8 (Color online) Grouting pressure distribution under different section flows

表9 截面流量对浆液压力分布的影响

Table 9 Impact of section flow on grouting pressure distribution 单位：MPa

q/(m3·s-1)0°30°45°55°60°90°120°125°135°150°180°0．004350．2000．2040．2160．2300．2360．2790．3220．3400．3510．3630．3700．005220．2000．2030．2140．2300．2360．2770．3180．3400．3500．3610．3700．005800．2000．2020．2120．2300．2360．2760．3160．3400．3500．3600．370

由图8可得，在45°位置，三者对应的浆液压力分别为0.216、0.214和0.212 MPa；在120°位置，三者对应的浆液压力分别为0.322、0.318和0.316 MPa；三者所对应的浆液压力分布曲线关系依次从外向内. 由此说明，截面流量越大，浆液压力越小.

4 结 论

综上研究可知：

1)本研究通过简化假定，采用力学方法推导盾构同步注浆压力分布统一计算模型，并将此模型推广到多孔注浆情形，使其具有普遍性和实用价值.

2)该分布模型可用于分析和评价浆液、注浆施工及盾构施工参数对浆液压力大小分布的影响，有益于指导工程实践.

3)工程实例分析表明，本研究推导的盾构同步注浆压力分布模型是合理的，且注浆浆液压力从拱顶至拱底呈非线性分布.小径盾构隧道宜采用四孔注浆，大径盾构隧道建议采用六孔或多孔注浆.

4)基于本研究推导的浆液压力分布模型，对浆液压力的主要影响因素进行了单因素敏感性分析，认为注浆孔越靠近拱顶位置，浆液压力越大，注浆孔越靠近拱底位置，浆液压力越小；盾尾间隙越大，浆液压力越大；截面流量越大，浆液压力越小.

引 文：邱明明，杨果林，姜安龙. 盾构隧道同步注浆的压力分布及其影响因素[J]. 深圳大学学报理工版，2015，32(2)：162-171.

参考文献 / References：

[1]Wang Mengshu. Develop ment of tunnel and underground space in 21th century in China[J]. Journal of Railway Science and Engineering，2004，1(1):7-8.(in Chinese) 王梦恕.21世纪我国隧道及地下空间发展的探讨[J].铁道科学工程学报，2004，1(1):7-8.

[2]Liu Jianhang，Hou Xueyuan. Shield driven tunnel[M]. Beijing: China Railway Publishing House，1991.(in Chinese) 刘建航，侯学渊. 盾构法隧道[M]. 北京: 中国铁道出版社，1991.

[3]He Chuan，Zeng Dongyang. Shield tunnel structure design and effect of construction on the environment[M]. Chengdu: Xi’nan Jiaotong University Press，2007.(in Chinese) 何 川，曾东洋.盾构隧道结构设计及施工对环境的影响[M].成都:西南交通大学出版社，2007.

[4]Qiu Mingming. Research on the stratum deformation prediction induced by metro shield tunnel construction [D]. Nanchang: Nanchang Hangkong University，2013.(in Chinese) 邱明明.城市地铁隧道盾构施工引起的地层变形预测研究[D]. 南昌:南昌航空大学，2013.

[5]Ye Fei，Gou Changfei，Chen Zhi，et al. Ground surface deformation caused by synchronous grouting of shield tunnels[J]. Chinese Journal of Geotechnical Engineering，2014，36(4):618-624.(in Chinese) 叶 飞，苟长飞，陈 治，等.盾构隧道同步注浆引起的地表变形分析[J]. 岩土工程学报，2014，36(4):618-624.

[6]Tang Mengxiong，Chen Rugui，Chen Wei. Stress monitoring and internal force analysis of Guangzhou metro shield tunnel segment during construction[J]. China Civil Engineering Journal，2009，42(3):119-124.(in Chinese) 唐孟雄，陈如桂，陈 伟. 广州地铁盾构隧道施工中管片受力监测与分析[J].土木工程学报，2009，42(3):119-124.

[7]Society of Civil Engineering of Japan. Standard specification for tunnelling (shield tunnels) and its definition[M]. Zhu Wei translate. Beijing: China Architecture & Building Press，2011:189-190.(in Chinese) 日本土木学会. 隧道标准规范(盾构篇)及解说[M]. 朱 伟,译.北京:中国建筑工业出版社，2011:189-190.

[8]Wan Zhansheng，Zhu Daiyun，Xia Yongxu. Numerical simulation study of settlement on shield tunnel after grouting of wall formation[J]. Journal of Hebei University of Technology，2011，40(1):110-113.(in Chinese) 万战胜，朱岱云，夏永旭.盾构隧道壁后注浆对地表沉降影响数值模拟研究[J].河北工业大学学报，2011，40(1):110-113.

[9]Li Fangnan，Shen Shuilong，Luo Chunyong. Prediction approach of ground deformation induced by pipe jacking construction considering grouting pressure[J]. Rock and Soil Mechanics，2012，33(1):204-208.(in Chinese) 李方楠，沈水龙，罗春泳.考虑注浆压力的顶管施工引起土体变形计算方法[J].岩土力学，2012，33(1):204-208.

[10]Sun Chuang，Zhang Jianjun，Liu Jiashun，el at. Effect of shield tunnel backfill grouting pressure on the ground surface subsidence[J]. Journal of Yangtze River Scientific Research Institute，2012，29(11):68-72.(in Chinese) 孙 闯，张建俊，刘家顺，等. 盾构隧道壁后注浆压力对地表沉降的影响分析[J].长江科学院院报，2012，29(11):68-72.

[11]Zhou Ye. Application of two-compoment backward split grouting to the Humaling Tunnel in water-rich fine sand[J]. Modern Tunnelling Technology，2012，49(4):165-169.(in Chinese) 周 烨.双液回退劈裂注浆在胡麻岭隧道富水粉细砂地层中的应用[J].现代隧道技术，2012，49(4):165-169.

[12]Song Tiantian，Zhou Shunhua，Xu Runze. Mechanism and determination of parameters of synchronous grouting in shield tunneling[J].Chinese Journal of Underground Space and Engineering，2007，4(1):130-133.(in Chinese) 宋天田，周顺华，徐润泽. 盾构隧道盾尾同步注浆机理与注浆参数的确定[J].地下空间与工程学报，2007，4(1):130-133.

[13]Wei Xinjiang，Hong Jie，Wei Gang. Research on DOT shield tunnel back-filled synchronous grouting diffusion and segments circumferential pressure distribution[J]. Journal of Wuhan University of Technology，2012，34(10):106-110.(in Chinese) 魏新江，洪 杰，魏 纲. 双圆盾构隧道同步注浆扩散及环向压力研究[J].武汉理工大学学报，2012，34(10):106-110.

[14]Koyama Y. Present status and technology of shield tunnelling method in Japan[J]. Tunnelling and Underground Space Technology，2003，18(2/3): 145-159.

[15]Kasper T，Meschke G. On the influence of face pressure，grouting pressure and TBM design in soft ground tunneling[J]. Tunnelling and Underground Space Technology，2006，21(2): 160-171.

[16]Working Group 2 of International Tunnelling Association. Guidelines for the design of shield tunnel lining[J]. Tunnelling and Underground Space Technology，2000，15(3): 303-331.

[17]Zhu Hehua，Cui Maoyu，Yang Jinsong. Design model for shield lining segments and distribution of load[J]. Chinese Journal of Geotechnical Engineering，2000，22(2):190-194.(in Chinese) 朱合华，崔茂玉，杨金松.盾构衬砌管片的设计模型与荷载分布的研究关[J]. 岩土工程学报，2000，22(2):190-194.

[18]Guan Linxing，Zhu Hehua，Yu Ning. Analysis of internal force of shield lining in cross-section considering load combination[J]. Rock and Soil Mechanics，2004，25(8):1302-1306.(in Chinese) 官林星，朱合华，于 宁. 考虑荷载工况组合的盾构衬砌横向受力分析[J]. 岩土力学，2004，25(8):1302-1306.

[19]Ye Fei，Zhu Hehua，Ding Wenqi. Analysis and control of upward moving of shield tunnel under construction[J]. Journal of Tongji University Natural Science，2008，36(6):738-743.(in Chinese) 叶 飞，朱合华，丁文其，等. 施工期盾构隧道上浮机理与控制对策分析[J]. 同济大学学报自然科学版，2008，36(6):738-743.

[20]Ye Fei，Zhu Hehua，He Chuan. Back-filled grouts diffusion model and its pressure to segments of shield tunnel[J]. Rock and Soil Mechanics，2009，30(5):1307-1312.(in Chinese) 叶 飞，朱合华，何 川.盾构隧道壁后注浆扩散模式及对管片的压力分析[J].岩土力学，2009，30(5):1307-1312.

[21]Ye Fei，Liu Yanpeng，Gou Changfei，et al. Capillary Penetration diffusion model for backfill grouting of shield tunnel[J]. Journal of Southwest Jiaotong University，2013，48(3):428-434.(in Chinese) 叶 飞，刘燕鹏，苟长飞，等.盾构隧道壁后注浆浆液毛细管渗透扩散模型[J]. 西南交通大学学报, 2013，48(3):428-434.

[22]Yuan Xiaohui，Han Yuewang，Zhong Xiaochun. Pressure distribution model of simultaneous backfill grouting of shield tunnel[J]. Journal of Southwest Jiaotong University，2011，46(1):18-23.(in Chinese) 袁小会，韩月旺，钟小春. 盾构隧道壁后注浆压力分布模型[J].西南交通大学学报，2011，46(1):18-23.

[23]Bai Yun，Dai Zhiren，Zhang Shasha，et al. Study on grout pressure dissipation mode in simultaneous backfill grouting during shield tunneling[J].China Railway Science，2011，32(4):38-45.(in Chinese) 白 云，戴志仁，张莎莎，等.盾构隧道同步注浆浆液压力扩散模式研究[J].中国铁道科学,2011，32(4):38-45.

[24]Zhang Shasha，Dai Zhiren，Bai Yun. Research on the dissipation law of grout pressure during the simultaneous grouting of shield tunnel[J]. China Railway Science，2012，33(3) :40-48.(in Chinese) 张莎莎，戴志仁，白 云.盾构隧道同步注浆浆液压力消散规律研究[J]. 中国铁道科学，2012，33(3) :40-48.

[25]Qiu Mingming，Jiang Anlong. Backfill grout pressure distribution model for a metro shield tunnel[J]. Modern Tunnelling Technology，2013，50(4): 115-121.(in Chinese) 邱明明，姜安龙.地铁盾构隧道壁后注浆浆液压力分布模型[J].现代隧道技术，2013，50(4): 115-121.

[26]Liu Henian. Fluid mechanics[M]. Beijing: China Architecture & Building Press，2002: 61-93.(in Chinese) 刘鹤年. 流体力学[M]. 北京:中国建筑工业出版 社，2002:61-93.

[27]Bezuijen A，Talmon A M，Kaalberg F J，et al. Field measurements of grout pressures during tunnelling of the Sophia rail tunnel[J]. Soils and Foundations，2004，44(1): 39-48.

【中文责编：坪 梓；英文责编：之 聿】

Influence factors and pressure distribution of simultaneous grouting for shield tunnel

Qiu Mingming1, Yang Guolin1†, and Jiang Anlong2

1) School of Civil Engineering, Central South University, Changsha 410075, P.R.China 2) Xiamen Rail Transit Group Limited Corporation, Xiamen 361001, Fujian Province, P.R.China

This paper deals with the circumferential simultaneous grouting process by the tail of the tunnel boring machine (TBM) tail in practices of subway tunnels constructed by TBM. We establish the mechanical model of grout pressure at any point in the circumferential section, and derive the unified computation model of grout pressure distribution during circumferential filling by assuming that grouts are Bingham fluids. Then, using the basic principle of mechanical model and limit equilibrium method, we extend the computation model to multiple holes grouting. The grout pressure distribution model is verified by an engineering case. The analysis results indicate that four-holes grouting is suitable for smaller diameter tunnel, and six-holes grouting or multiple-holes grouting are good for larger diameter tunnel. Grouting hole position, TBM tail interspaces, and section flow have important impact on grout pressure distribution and thus deserve much attention in tunnel engineering.

tunnel engineering; tunnel boring machine(TBM); simultaneous grouting; TBM tail interspace; pressure distribution; metro construction

：Qiu Mingming，Yang Guolin，Jiang Anlong. Influence factors and pressure distribution of simultaneous grouting for shield tunnel[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 162-171.(in Chinese)

U 451

A

10.3724/SP.J.1249.2015.02162

国家自然科学基金资助项目(51478484，51278499)

邱明明(1985—)，男(汉族)，陕西省商洛市人，中南大学博士研究生.E-mail: sxdfqiuming@163.com

Received：2014-10-24；Accepted：2015-01-09

Foundation：National Natural Science Foundation of China (51478484，51278499)

† Corresponding author：Professor Yang Guolin. E-mail: guoling@mail.csu.edu.cn