无粘结柔性管抗拉伸层结构分析
2015-04-25杨旭孙丽萍李鹤楠
杨旭,孙丽萍,李鹤楠
(1哈尔滨工程大学船舶工程学院,哈尔滨150001;2挪威科技大学海洋技术系,挪威特隆赫姆7491)
无粘结柔性管抗拉伸层结构分析
杨旭1,孙丽萍1,李鹤楠2
(1哈尔滨工程大学船舶工程学院,哈尔滨150001;2挪威科技大学海洋技术系,挪威特隆赫姆7491)
柔性管抗拉伸层是复杂的空间螺旋线结构,其结构响应分析对柔性管疲劳分析、强度分析和屈曲分析有重要作用。文章基于曲梁理论,应用斜驶螺旋线假设和测地线假设两种空间曲线公式,以空间细长杆理论及胡克定律本构方程为基础,采用格林应变张量与第二Kirchoff应力张量度量,对深海无粘结柔性管抗拉伸层螺旋形钢缆结构平衡方程进行了推导,编写了分析程序。利用该程序,分析了抗拉伸层钢缆在轴对称载荷下和弯矩作用下的曲率变化和结构响应;同时利用三维直梁有限元模型与曲梁有限元模型建立数值模型,将程序结果与数值模拟模型结果进行了对比,证明了结果可行性。该结果可为柔性管抗拉伸层结构设计提供快速的预估计方法。
柔性管;抗拉伸层;斜驶线;测地线;结构分析
0 引言
立管和海底管道作为海洋石油工业的“生命线”,承担着油气水运输的重要任务。无粘结柔性管可作为柔性立管或海底管道,具有结构布置形式灵活、顺应性强、与平台耦合较弱、安装与回收成本低等诸多优点,在挪威北海、巴西以及美国墨西哥湾等恶劣深海环境下被广泛运用。无粘结柔性管为多层复合结构,一般而言从内到外可分为内衬层(Internal Carcass)、内压防护层(Internal Pressure)、内锁压力层(Pressure Armor)、抗磨层(Anti-wear tape)、抗拉层(Tensile Armor)和外保护层(Outer Sheath);此外在一些层与层之间还存在用聚酯纤维制作的中介保护层。柔性管的截面形式如图1所示,其各层结构均有特定的用途[1]。
无粘结柔性管抗拉伸层一般有两层,由多条螺旋形高强度钢缆绕制而成。在工作状况下,抗拉伸钢缆主要用于抵抗轴向拉力以及部分外压和弯矩。由于结构形式为空间曲线,又存在多种相互接触以及不同材料,抗拉伸层钢缆结构分析一直是研究热点。对于其相关研究,Hector等[2]运用ANSYS软件模拟了柔性管受拉力与扭矩时的结构响应,以弹簧单元和面对面接触单元模拟抗拉伸层与各层之间的接触。将抗拉伸层作为三维直梁单元考虑,并添加大量的接触单元。这样做无疑会加大计算时间,同时为单元带来了初始几何缺陷。部分研究人员选择了更适合于螺旋线缆的细长杆理论,将钢缆假设为沿空间曲线的螺旋梁。Svein[3]运用细长杆理论建立了适于模拟抗拉伸层的新型曲梁单元,进行了轴对称载荷下的结构分析;并进行了轴对称载荷与弯矩作用下的疲劳分析。Østergaard[4]假设单根螺旋钢缆满足无摩擦的测地线假设,对柔性管在受压和弯曲过程中可能产生的失稳进行了分析。Yan与Lun[5]通过加入人工系数CP对测地线假设结果进行修正,以此模拟钢缆在弯曲过程中的摩擦力。
本文基于非线性空间细长杆理论,将螺旋抗拉伸层钢缆考虑为空间曲线,建立了抗拉伸层解析解模型,运用MATLAB语言编写了抗拉伸层结构响应分析程序。依据基本假设不同,建立了两种解析解模型:一种假设变形后的抗拉伸螺旋钢缆符合变形规律满足测地线假设(geodesic assumption);一种假设变形后满足斜驶螺旋线假设(loxodromic assumption)。求解了在轴对称载荷下以及受弯矩情况下的解析解。获得了抗拉伸层在不同载荷下的位移与曲率。利用BFLEX软件建立了数值模拟模型,与解析解进行了对比,在小变形阶段结果较为接近。
1 理论推导
1.1 理论背景与基本假设
本文推导的抗拉伸层运动方程是以细长杆理论为基础。其基本理论为假设空间结构是一细长体,以弧长s和时间t为基本变量,假设其他变量为其函数,建立以切向,法向,副法向为坐标轴的曲面坐标系,通过求解空间曲线的曲率变化获得结构响应。该方法适合分析沿空间曲面变化的细长体结构。该理论最早可追溯到Kirchoff的线性细长杆理论,后由Ericksen等[6]发展为非线性理论。Washizu[7]运用格林应变张量与Kirchoff应力张量、胡克定律与虚功原理得到了线性细长体理论下的应力应变。Svein[8]此后将其延伸到大变形小应变范围,并应用于柔性管的应力分析。本文在其基础上进行分析。根据相关理论,采用如下基本假设:
(1)抗拉伸层螺旋钢缆假设为细长体,根据一般柔性管的长度和抗拉伸层尺寸,这一假设是合理的。
(2)每一根钢缆是独立的,不考虑其与其他钢缆间相互作用。这一假设适用于柔性管曲率小于临界曲率时,符合工程计算的一般情况。当结构变形过大,各钢缆直接可能产生接触力。
(3)以一根或几根螺旋钢缆的结果代表整个抗拉伸层结构响应,忽略柔性管道的椭圆化。该假设可大幅减少计算时间,同时基本保证计算精度,被众多研究学者采用。由于柔性管截面中心线对称,所以该假设在轴对称载荷下影响可忽略。当考虑弯矩作用时,会对计算结果有一定影响。
(4)不考虑层与层之间的摩擦作用。虽然摩擦作用在受弯矩载荷情况下被普遍认为具有重要作用,但为节约计算成本,本解析解并没有考虑摩擦作用。可在解平衡方程时进行系数修正,获得更符合实际的结果。
1.2 空间细长杆应力应变
假设螺旋钢缆为一空间细长杆。其横截面上有任意一点P,依据螺旋方向建立局部曲面坐标系,以切向量,法向量,副法线向量为基坐标向量,坐标系如图2所示。则P点位移方程可按下式表示:
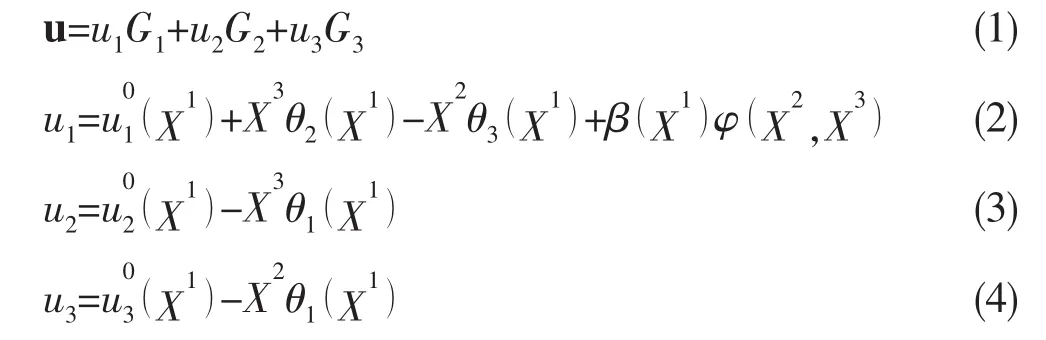
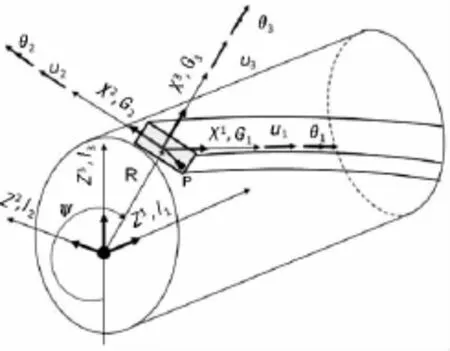
图2 局部坐标系与总体坐标系[8]Fig.2 Local coordinate system and global coordinate system[8]
其中:ui为沿局部坐标系下位移分量,Gi为沿曲线切线,法线副法线组成的局部坐标系基向量。上角标0表示位移沿中心线变化的相关分量,在下文中将被推导。X1为弧长变量,φ(X2,X3)代表与梁横截面相关的翘曲方程;依据圣维南假设,β为常量。由Frenet-Serret公式可得:

式中:κi代表螺旋线的曲率分量。
根据Svein[3]的研究,选用格林应变张量作为结构的应变表达式,以细长杆中同一原点建立相应的局部笛卡尔直角坐标系,若将笛卡尔坐标系与曲坐标系基向量分别设为Xi与Yi,则运用张量转化公式可得:

其中:Eij′表示曲线坐标系下的Green应变张量,Eij表示笛卡尔坐标系下的结果。
对抗拉伸层应用如下假设:
(1)假设钢缆的截面为中心对称的,这在现今的柔性管设计中都可以保证。
(2)忽略格林应变中非重要的二阶项。
(3)应用欧拉伯努利梁假设(平断面假设)。
将假设代入(7)式可得:
本文中下角标“,i”表示该量对曲线坐标系下相应基向量求导。ε1表示由于轴向和横向位移产生的轴向应变,ε2和ε3表示由于中心线旋转产生的应变分量。△κi表示弧长变化dX1产生的i方向曲率增量。由欧拉伯努利梁基本假设,消去θ2和θ3。G为基本张量行列式,表达式如下:

各变量按中心线位移与空间曲线曲率表示为:
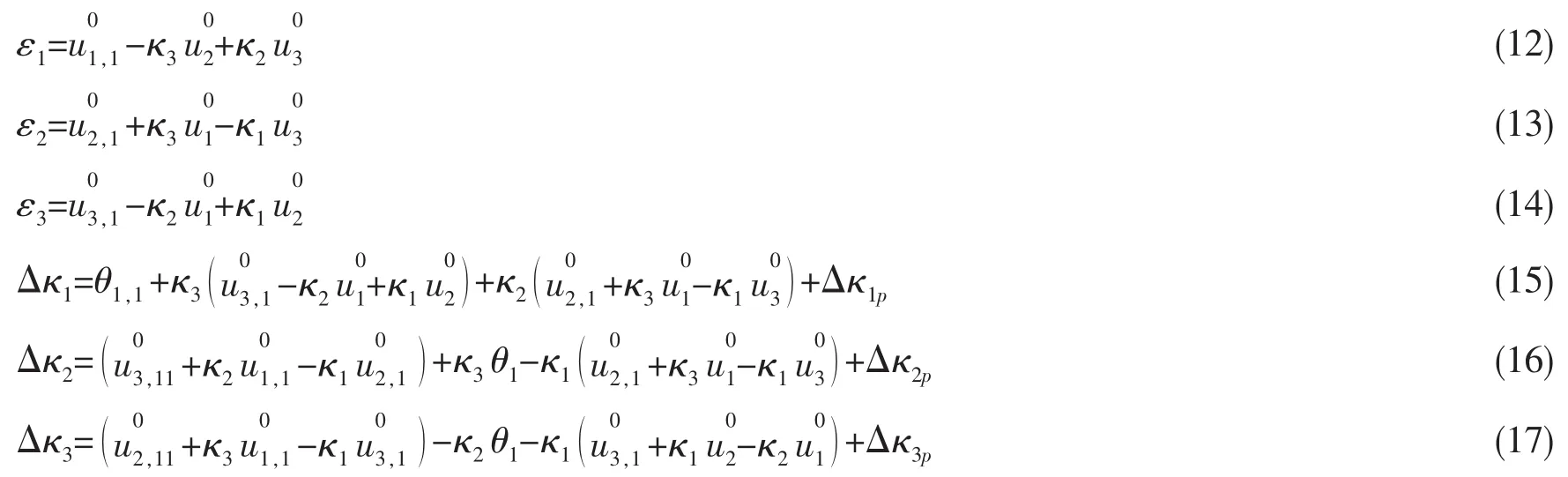
采用二阶Kirchoff应力张量S与上文的格林应变张量E作为应力与应变测量值,假设相互关系满足胡克定律,则可得本构关系方程。至此,即可运用钢缆的沿弧长的曲率变化值求出其应变值,再推导出应力值。
1.3 虚位移原理与平衡方程
本文采用虚位移原理进行求解。虚位移原理为弹性力学中的经典原理,即对结构加以微小虚拟位移获得平衡方程。根据虚位移原理可推出结构内力虚功为:
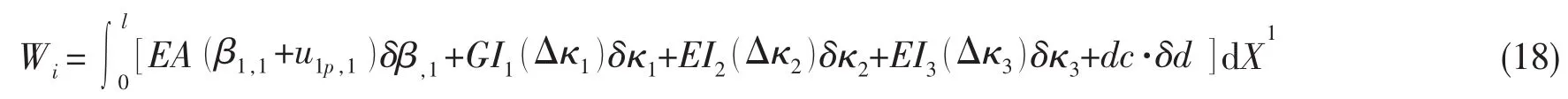
其中:Wi表示内力虚功,A为细长螺旋杆截面积,β表示螺旋杆与管中心线产生的相对位移,d为修正摩擦系数,c为表示两者相互摩擦关系张量。在本文中由于忽略摩擦作用,因此都可设为0。曲率变化值△κi=△κiu+△κip,△κip为螺旋钢缆按照假定曲线(斜驶线或测地线)变化形成的曲率变化分量,△κiu为由于层与层间相互作用使钢缆在假定曲线基础上产生相对滑移,由此产生的曲率变化。本文中假设△κiu=0。据此公式,利用三点高斯积分公式即可获得某一段细长杆件的内力做功。
取细长杆件的一个微小分段X1进行受力分析,如图3所示,由此可获得力与力矩平衡方程如下:
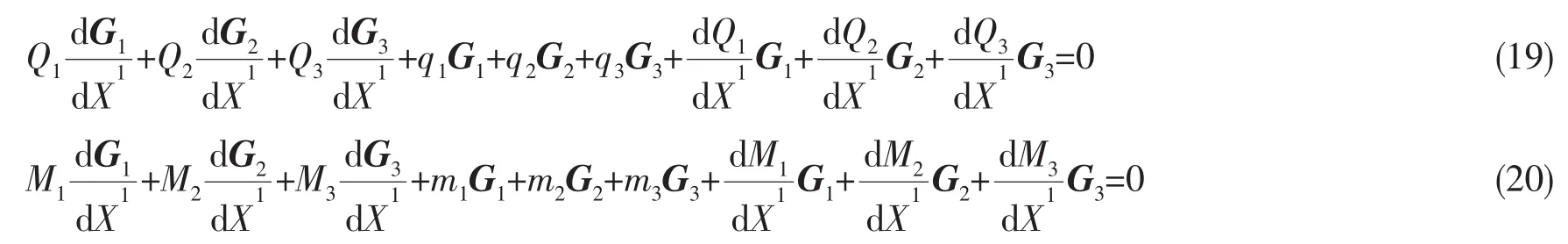
利用(5)式即可将其改写为六个平衡方程。
1.4 运动限制方程
本文假设钢缆的变化曲面为以管中心为中心线的圆柱曲面,且半径不变。该假设在进行小变形受拉扭载荷时影响不大;在进行屈曲分析以及考虑两端作用时会造成结果不准确,但为了便于获得钢缆结构响应,首先进行以上假设,在今后研究中再进行修正。由此可简化全三维结构,为确保钢缆移动仅
在曲面上,需加入运动限制方程:

其中:κh为圆柱表面横向曲率分量,由欧拉方程得:

式中:κr,κc分别为中心曲面在径向和轴向上的曲率分量。
1.5 测地线假设
测地线来源于地理学,数学上表示在空间曲面上最短的一条线,可视作曲线在弯曲空间的推广。在结构分析中,若假设结构在曲面上沿测地线假设运动,则表示结构仅被限制于曲面内,即无摩擦作用和其他限制。以曲面中心线角度φ以及螺旋线绕中心线转过的角度ν和中心线曲率半径ρ表示中心线笛卡尔坐标系分量如下:

则弧长S对于笛卡尔坐标系分量的微分可表示为

若假设螺旋形钢缆追随测地线变化,则其长度可由微分几何获得。将空间曲线弧长dS积分并转换为上述变量表示,加入Lagrange乘子λ,利用最优化理论解得

其中:C为积分常量。不妨设ν=π/2,则

由此可解得C。将φ,1以R/ρ为展开项进行泰勒展开,忽略高阶项,沿弧长重新积分可得

另有沿曲线坐标关系方程

将(28)、(29)式结合,解得

其中第二项即为ν的变化值,则总相对位移可得

各方向位移分量为

上式表明了当曲面中心线存在一定的曲率半径时,若假设钢缆沿测地线变化,则钢缆会产生侧向滑移与轴向滑移,其滑移值与曲率半径,螺旋角和所在方位相关。整个轴向滑移从受压缩到受拉伸不断变化。
事实上,若钢缆在圆柱表面符合测地线假设移动,其会产生一定的扭转角,产生一定的应力;由于前文中假设钢缆法向量与曲面法向量相同,因此该应力会导致所求结果与实际结果存在一定偏差。Svein[3]讨论了这种偏差的影响,指出当结构受到轴向拉力时,这种偏差会显著减小0.1°以下,可以忽略。结构所需的轴向拉力大小取决于结构形式以及螺旋线布置角,若布置角大于30°,则所需轴向拉力大幅度减小。因本文考虑结构受到拉力与弯矩作用,故忽略这种影响,认为运动限制方程有效。
综合上述公式解得满足测地线假设的螺旋钢缆曲率增量为:

若柔性管仅受拉压载荷,则曲率半径无穷大,管道模型为轴对称模型。由(12)-(17)式可得螺旋线轴向应变与管中心轴轴向应变方程以及轴对称载荷下曲率变化方程:

其中:εz表示柔性管中心轴的轴向应变。再结合空间几何关系,最终可得曲率变化:
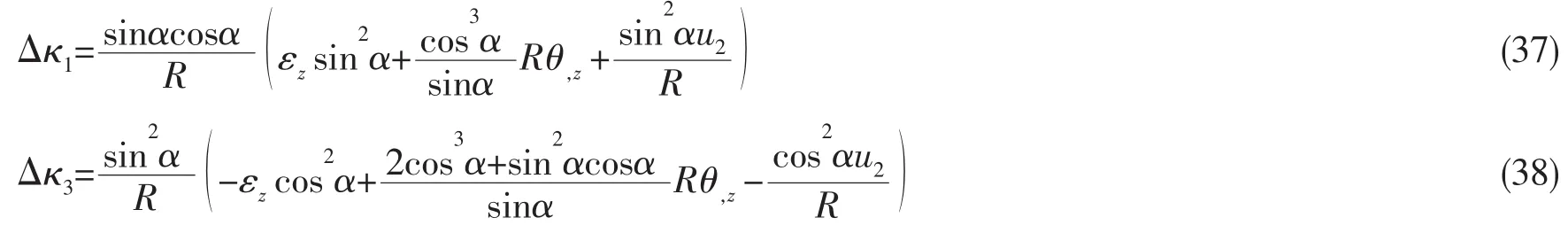
1.6 斜驶线假设
斜驶线的概念同样来源于地理学,表示该空间曲线与曲面坐标轴所成角度不变,即螺旋角α不变。斜驶线与测地线在球体上的表示如图4所示。在物理学上,可视为空间曲线结构与所在曲面无相对滑移,即摩擦力无穷大。当空间曲面弯曲变化时,由于受到轴向应力作用,原坐标系基向量G1的模也会随之变化,设变化后的基向量为g1,由(6)式可得格林张量值,代入基向量中可得:
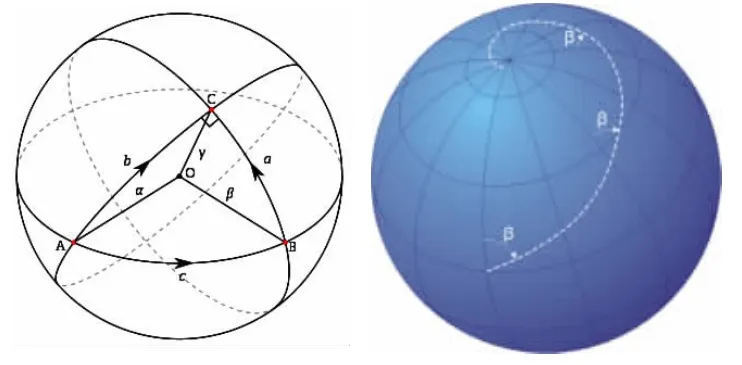
图4 测地线(左)与斜驶线(右)Fig.4 Geodesic curve(left)and loxodromiccurve(right)


利用测地线假设与斜驶螺旋线假设下的曲率变化方程,可求解受到环境载荷之后的抗拉伸层钢丝新曲率值。再由曲面坐标系下的应力应变关系,求解出各点应力,通过三点高斯积分,即可获得抗拉伸层钢丝弯矩和剪力。将整个过程不断迭代,并应用新的螺旋角,即可得到抗拉伸层钢缆结构响应的准静态公式。
2 数值模拟实例
根据前文所述的公式,以MATLAB程序语言编写了结构分析程序代码TensileArmorV1.M。该程序以准静态线性方法,分析抗拉伸层钢缆的曲率变化,再通过上文公式导出弯矩和剪力值。程序中忽略摩擦作用以及钢缆与管其它层间作用,假定钢缆符合上文所述各种假设。程序流程图如图5所示。
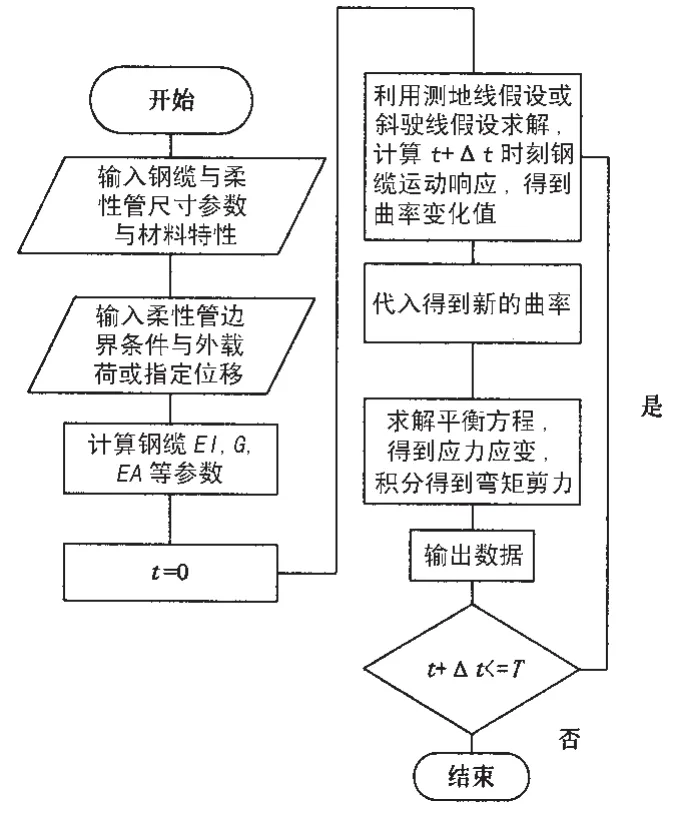
图5 结构分析程序流程图Fig.5 Flow diagram of program TensilearmorV1.m

图6 ABAQUS有限元模型Fig.6 Finite element model of ABAQUS
本文选择一根柔性管作为实例分析。其抗拉伸层直径为100 mm,抗拉伸层横截面为长方形,厚3 mm,宽10 mm,布置角度为30°。材料为高强度碳钢,本文假设为满足胡克定律的弹性材料,杨氏模量E=211 GPa,屈服应力1 100 MPa,泊松比0.3。文中选择4倍螺距长度进行分析。由于程序仅分析单根抗拉伸钢缆作用,本文将其它层作用假设为管道位移边界条件施加到抗拉伸层中;管道模型曲率按从0 m-1到0.1 m-1循环变化。
为对比分析不同模型差异,本文运用ABAQUS通用有限元软件隐式计算模块,建立了以三维直梁单元(B31)为基础的有限元模型。模型的材料,截面参数与边界条件与前文相同。采用SHELL单元代表整个柔性管结构。同样采用一根等效抗拉伸层钢缆进行分析。钢缆按长度方向被分为100个单元,每个单元节点与对应的表面运用Tie连接,以此实现斜驶螺旋线假设。加载步骤为先匀速缓慢加入轴向拉力,再缓慢施加弯矩循环。其中轴向拉力部分为静态分析,弯矩循环部分为动态分析。所得模型如图6所示。
BFLEX管道分析软件是MARINTEK水池开发的,依据空间曲梁原理与斜驶螺旋线假设以及非线性有限元框架编写的有限元结构分析软件。采用该软件建立类似模型与本文结果和ABAQUS模型进行对比。BFLEX模型采用100个H353单元,该单元为曲梁单元。同时考虑管道与抗拉伸层的摩擦,摩擦系数设为0.4,采用较高摩擦系数近似模拟斜驶螺旋线的摩擦无限大假设。其他参数与ABAQUS模型相同。所得模型如图7。

图7 BFLEX有限元模型Fig.7 Finite element model of BFLEX
3 结果与讨论
3.1 轴对称载荷结果分析
当柔性管仅受轴向拉力时,柔性管抗拉伸钢缆在局部坐标系下的曲率变化结果如图8和图9所示。轴向拉力以指定位移匀速施加在管中心轴上,从0匀速增加至1%管长。从图中可得,切向与纵向曲率变化随轴向拉力基本呈线性变化,三个模型趋势相同,结果近似,证实了本文模型的可行性。采用直梁单元的ABAQUS模型曲率变化更大。BFLEX模型与本文模型由于基本方程相同,所以变化不大。差异主要是由于数值模型中采用非线性计算方法,同时布置角α会随轴向应变不断变化;而本文程序采用线性计算,同时假设α为一定值。径向曲率变化值如图10,按照BFLEX与本文假设,径向曲率变化率为0。由于直梁模型为近似模拟螺旋曲线,故在ABAQUS模型中存在较小的曲率变化,但数量级为10-5m-1,可以忽略不计。图11表示了抗拉伸钢缆在拉力作用下的轴向力。图12表示了BFLEX模型当拉力最大时抗拉伸层钢缆关于管道中心轴的弯矩分布。ABAQUS模型与本文程序所得弯矩分布与该图类似。本文选择弯矩最大处进行对比分析,结果如图13。弯矩与轴力图表明以格林应变张量与第二Kirchoff应力张量度量并运用坐标系转化这一方法是切实可行的。
对于计算效率的比较,本文选择一台Intel I7 4核处理器,32 GB内存进行计算,本文模型计算时间约10 s,BFLEX模型计算时间约100 s,ABAQUS模型计算时间约为600 s。由于采用了针对柔性管的坐标系与单元,本文模型计算时间大大减少。
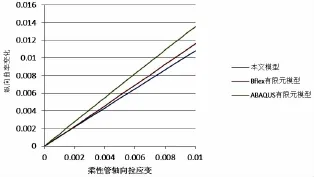
图8 轴向拉力下螺旋钢缆纵向曲率变化Fig.8 Axial curvature increment in tensile load condition
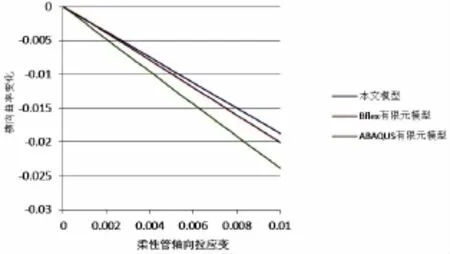
图9 轴向拉力下螺旋钢缆横向曲率变化Fig.9 Transverse curvature increment in tensile load condition
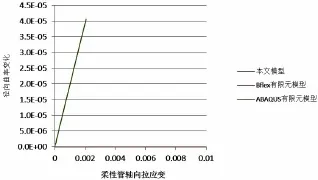
图10 轴向拉力下螺旋钢缆径向曲率变化Fig.10 Radical curvature increment in tensile load condition
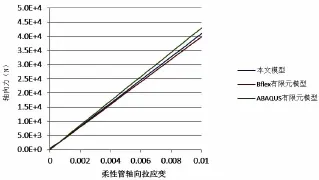
图11 轴向拉力下螺旋钢缆轴力Fig.11 Axial force of tensile armor wire

图12 关于管中心轴弯矩分布图Fig.12 X(m)versus Moment-Z(N*m)

图13 关于中心轴最大弯矩对比图Fig.13 Maximum moment about center core
3.2 弯曲载荷下结果分析
对柔性管两端施加弯矩使其曲率从0 m-1到0.1 m-1缓慢增加,以近似于三角函数循环变化。在弯矩施加前对柔性管施加0.15%的拉应变以保证整个弯矩作用时柔性管状态稳定,避免发生屈曲。在Bflex模型中选择摩擦系数miu分别为0与0.4用以分别对比测地线假设与斜驶螺旋线假设的情况。在ABAQUS模型中运用tie连接将抗拉伸钢缆与表面相连,以此来模拟斜驶螺旋线假设。同时在程序中分别算出斜驶螺旋线与测地线假设结果。
本文以曲率达到最大值时结果进行分析。数值模拟所得抗拉伸钢缆相对于中心管轴向位移如图14。轴向位移随着螺旋的循环不断循环变化,周期为一个螺距。在螺旋开始端为0,在1/4螺距处达到最大值。根据假设,斜驶线与ABAQUS模型的横向位移为0 mm。摩擦系数为0.4的BFLEX模型较为接近斜驶线假设模型,幅值为0.4 mm。而摩擦系数为0的BFLEX模型则比测地线假设略大,幅值分别为2.5 mm与2 mm。横向相对位移沿管长变化如图15所示,所得结果同样以单螺距为周期循环变化。斜驶线模型,高摩擦系数模型与ABAQUS模型结果基本相同,符合假设预期。
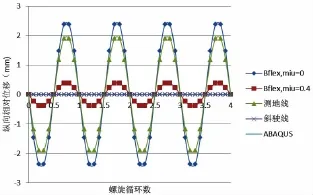
图14 纵向相对位移沿管长分布图Fig.14 Pitch times versus relative displacement(mm) in axial direction
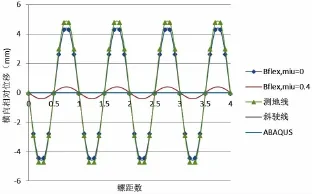
图15 横向相对位移沿管长分布图Fig.15 Pitch times versus relative displacement(mm) in transverse direction
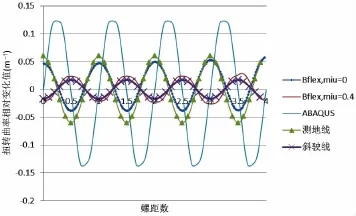
图16 扭转曲率相对变化值沿管长分布图Fig.16 Pitch times versus relative twist curvature(m-1)
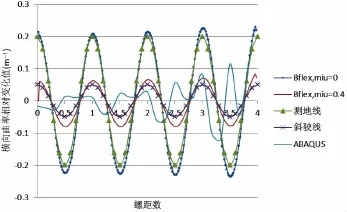
图17 横向曲率相对变化值沿管长分布图Fig.17 Pitch times versus relative transverse curvature(m-1)
图16表示扭转方向曲率相对变化值Δκ1沿管长方向分布图。测地线曲率变化值呈余弦函数分布,周期为单位螺距,幅值约为0.05 m-1;与无摩擦BFLEX模型近似。斜驶线模型与高摩擦模型近似,相位角与测地线假设相反,幅值较小,约为0.02 m-1。ABAQUS模型变化值呈正弦函数分布,周期与其他模型相同,幅值略大,约为0.12 m-1。产生差异原因可能是ABAQUS模型采用直梁单元,其初始梁单元方向仅能代表该微段梁单元的平均方向,而不能代表起始点准确方向,因此在弯曲作用下曲率变化较为敏感。由于结果显示为曲率相对变化值,故对实际梁运动影响不大。但在屈曲分析或疲劳分析中,需考虑管道受长时间多次弯曲循环作用,该微小差异可能导致直梁有限元结果与其他基于空间细长体结果产生不同。图17表示横向曲率相对变化管长分布。由于边界作用,ABAQUS与BFLEX模型在边界上出现小幅波动,但对结果影响较小。测地线结果与0摩擦模型相似;斜驶线模型与高摩擦模型相似,符合假设预期。所有细长杆模型结果均类似于以单螺距为周期的余弦函数。由于测地线假设摩擦为0,因此横向曲率变化较斜驶线假设大,幅值分别为0.2 m-1与0.04 m-1。直梁模型结果曲率变化平均值约为0 m-1,与斜驶线近似,不同之处在于结果周期性不明显,分布不稳定,这与直梁模型近似表示空间曲线结构相关。图18为径向曲率变化值对比图。结果同样较为符合,测地线曲率变化较斜驶线大。ABAQUS模型结果与斜驶线模型近似,但分布不稳定,原因与上文相同。
上述结果表明测地线假设可代表摩擦为0时抗拉伸螺旋管的位移变化;而斜驶线假设则可基本代表高摩擦系数时抗拉伸层位移变化。工程实际中摩擦系数在0与无限大之间;因此可通过该程序的两种假设模型快速估算出抗拉伸钢缆运动响应范围。在同上文相同计算机上,本文程序计算时间约为100 s,BFLEX约为900 s,ABAQUS达到2 000 s;表明本文程序计算效率较高。
4 结论
本文基于测地线假设与斜驶螺旋线假设,推导了柔性管抗拉伸层螺旋钢缆在轴对称载荷以及循环弯矩作用下的结构曲率变化方程组。同时,应用格林应变张量,二阶Kirchoff应力张量以及胡克定律,将格林应变张量在曲面坐标系下表示,并转化为局部坐标系,得出抗拉伸层钢缆弯矩,轴力公式。编写了线性准静态计算程序,选择柔性立管实例进行了分析。运用有限元软件建立了多个曲梁单元模型与直梁单元模型,与计算结果进行了对比,结论如下:
在柔性管受轴对称载荷时,计算结果表明局部坐标系x和y方向曲率变化值与拉应变呈线性关系。局部坐标系径向曲率基本为0。与通用直梁有限元模型以及曲梁单元模型对比,结果基本相同。本文假设成立,计算程序可行。
在受弯曲载荷时,斜驶线假设模型与高摩擦系数模型高度近似,证实了斜驶线假设符合高摩擦系数时螺旋钢缆运动响应。测地线假设模型与无摩擦模型结果近似,表面测地线假设模型可用于预测低摩擦系数时抗拉伸层运动响应。结果表明摩擦力对抗拉伸钢缆在弯曲作用下的结构响应有较大影响。直梁模型在位移上与斜驶线模型十分接近,在曲率变化上平均值与斜驶线模型接近,但分布规律较为不同;其原因主要是基本假设与单元特性造成偏差。在短时间弯曲分析中差异可忽略不计。在多次弯曲循环分析中,该差异可能引起曲梁模型与直梁模型结果不同,有待进一步验证。
在两种载荷分析中,本文模型都体现了较高的运行效率。工程上本程序可应用于轴对称载荷下抗拉伸钢缆设计;并快速分析抗拉伸钢缆在弯曲载荷下的运动响应范围,为抗拉伸钢缆设计提供参考。
在今后研究中将根据实验结果,增加修正系数建立结构响应与摩擦系数关系从而准确模拟抗拉伸层。同时,非线性动态计算方法,非线性材料模型以及螺旋线布置角的实时变化将被加入到今后的程序中。抗拉伸层与其他层之间的接触作用在本文中没有考虑,也将在进一步的研究中体现。
[1]杨旭,孙丽萍,艾尚茂.深水无粘结柔性管抗拉伸层屈曲问题研究进展[J].海洋工程,2013:31(1):99-106. Yang X,Sun L P,Ai S M.Recent research of deepwater unbounded flexible pipe tensile armor layer’s buckling behaviors[J].Ocean Engineering,2013:31(1):99-106.(in Chinese)
[2]Hector M,Jose S.,Carlos M,Ney R.On the coupled extensional torsional response of flexible pipes[C]//Proceedings of the ASME 2009 28th International Conference on Ocean,Offshore and Arctic Engineering.Hawaii,2009:1-13.
[3]Svein S.On stresses and fatigue in flexible pipes[D].Norway:Norwegian University of Science and Technology,1993: 2.1-2.42.
[4]Østergaard N H.On lateral buckling of armouring wires in flexible pipes[D].Denmark:Aalborg University,2012:1-10.
[5]Yangqiu Z,Lun Q.Numerical model to simulate tensile wire behavior in unbonded flexible pipe during bending[C]//Proceedings of the 26th International Conference on Ocean,Offshore and Arctic Engineering.USA,2007:1-13.
[6]Ericksen J,Truesdell C.Exact theory of stress and strain in rods and shells[J].Arch Rat Mech Anal,1957(1):295-323.
[7]Washizu K.Some considerations on a naturally curved and twisted slender beams[J].Journal of Math Phys,1964(43): 111-116.
[8]Svein S.Theoretical and experimental studies of stresses in flexible pipes[J].Computers and Structures,2011(89):2273-2291.
Analysis of tensile armor layer structural behaviors in flexible pipe
YANG Xu1,SUN Li-ping1,LI He-nan2
(1 Shipbuilding Engineering College,Harbin Engineering University,Harbin 150001,China; 2 Department of Marine Technology,Norwegian University of Science and Technology, Trondheim Norway 7491,Norway)
Tensile armor layers of flexible pipe are complex helix structures,whose stress analyses are significant to flexible pipe’s fatigue,strength and buckling behaviors.This paper is based on curved beam theory.Equilibrium equations of tensile armor wires in deepwater unbonded flexible pipe were solved with assumptions of loxodromic curve and geodesic curve,based on slender rod theory and elastic constitutive relationship.The curvatures and structural response under axisymmetric load and bend moment were analyzed.A three dimensions beam finite element model and a three dimensions curved beam element model were built by FEM software to compare with the results.The results show that the formulations and codes are reasonable for predicting structural responses of tensile armor wires.This solution provides a fast method to evaluate the stress and curvatures in design of flexible pipe’s preliminary design.
flexible pipe;tensile armor layer;loxodromic curve;geodesic curve;structural analysis
P756.2
A
10.3969/j.issn.1007-7294.2015.04.012
1007-7294(2015)04-0436-11
2014-09-22
FPSO和外输系统数值模拟及实验研究(2011ZX05030-006-002);国家建设高水平大学公派研究生项目;深海工程科学与技术创新引智基地(B07019)
杨旭(1987-),男,博士研究生;孙丽萍(1963-),女,教授,博士生导师,通讯作者,E-mail:sunliping@hrbeu.edu.cn;李鹤楠(1987-),女,硕士。
