热环境下功能梯度圆柱壳的频散特性

叶曦，孙永华，刘见华，姚熊亮

（1中国船舶及海洋工程设计研究院，上海200011；2哈尔滨工程大学船舶工程学院，哈尔滨150001）

热环境下功能梯度圆柱壳的频散特性

叶曦1，孙永华1，刘见华1，姚熊亮2

（1中国船舶及海洋工程设计研究院，上海200011；2哈尔滨工程大学船舶工程学院，哈尔滨150001）

基于经典壳体理论推导了温度场作用下功能梯度材料圆柱壳自由振动方程，研究了沿厚度方向不同温度分布对功能梯度壳体频散特性的影响。研究结果表明：以径向弯曲运动为主的传播波受热效应影响较为显著；温度效应对近场衰减波的影响随着频率的增大而减弱；共轭衰减波向近场衰减波转化的频率随着温度的升高而增大；与满足一维稳态热传导条件的温度分布相比，壳体最大温升相同时，均匀升温对壳体频散特性的影响较大。该文结果可为功能梯度材料结构在热环境中的波动特性研究提供参考。

圆柱壳；功能梯度材料；频散；热效应；体积分数指数

0 引言

功能梯度材料（FGMs）作为一种新型复合材料已被广泛应用于船舶、航天、能源等关键工程领域。与传统的复合材料不同，功能梯度材料的宏观理化特性在空间上按梯度变化，从而使材料两侧呈现截然不同的性能和功能，使结构能更好地适应复杂环境。功能梯度材料多工作于热环境下，且能保持良好的耐热性、抗热冲击性、抗热疲劳性、较高的机械强度和较好的力学性能。在材料高温侧采用耐热性较好的陶瓷材料，在低温侧采用导热性和强度较好的金属材料，可有效降低结构中的热应力。功能梯度材料对环境的良好适应性和材料本身的可调控性，使其拥有良好的开发和使用前景，加深对功能梯度材料典型结构（如圆柱壳结构）的认识和研究，具有较高的工程实用价值。

目前，国内外对功能梯度材料圆柱壳动态特性的研究已获得相当多的成果。Loy[1]首先利用壳体理论研究了功能梯度圆柱壳的自由振动，讨论了壳体参数以及功能梯度材料体积分数指数的变化对壳体固有频率的影响，但没有考虑温度效应对壳体固有动态特性的影响。Kadoli[2]和Haddadpour[3]研究了特定温度边界条件下的功能梯度圆柱壳热屈曲和自由振动特性,给出了不同结构边界条件下，温度改变对壳体最小自振频率的影响。频散效应是结构的固有波动特性，可由自由振动方程推得。现已有较多的文献对圆柱壳结构的频散特性[4-6]进行过研究。但是对热环境下功能梯度材料圆柱壳波传播特性的研究开展得还较少。当功能梯度圆柱壳两侧环境温度发生变化时，会引起壳体固有特性的改变。因此，可以通过适当改变壳体两侧温度，使结构的波动特性向有利的方向变化，达到对结构振动进行主动控制的目的。

本文研究指数型体积分数功能梯度圆柱壳在热环境下的振动波频散特性。基于经典壳体理论，采用波动法，推导沿厚度方向不同温度分布下，功能梯度圆柱壳的自由振动方程。以不锈钢/氧化锆复合而成的功能梯度材料圆柱壳为例，分析比较了不同温度分布及壳体材料参数对结构频散特性的影响。所得结果可为功能梯度材料应用于高温复杂环境下的波动特性研究提供参考。

1 基本理论

1.1 功能梯度材料基本特性

考虑由两种材料复合而成的功能梯度材料圆柱壳，如图1所示。两者的体积分数遵循指数变化率，由此功能梯度材料的特性Pe可表示为：

其中：P可表示杨氏模量E、密度ρ、泊松比μ、热传导系数κ和热膨胀系数α等；R为壳体中面半径；h为壳体厚度，h=Ro-Ri，下标i和o分别表示壳体内侧和外侧；N为体积分数指数，取值范围是[0，+∞）。

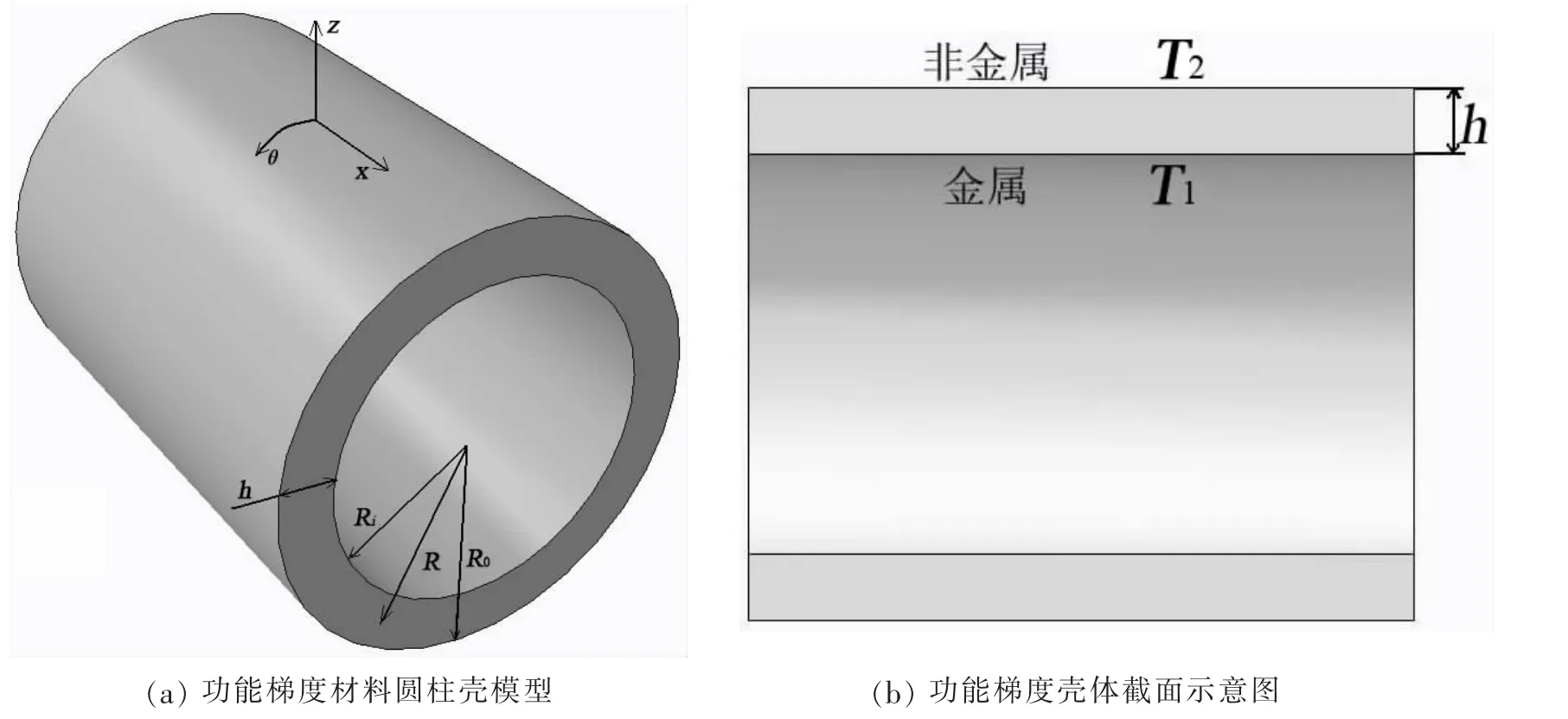
图1 功能梯度材料圆柱壳模型Fig.1 The model of FG cylindrical shells

功能梯度材料多工作于高温环境中，其组成材料的特性也大多是温度的函数，可用下式表示：

其中：T表示温度，单位是K；P0，P-1，P1，P2和P3为温度系数，其值和材料有关。为了计算方便，本文中假定E、ρ、α和κ为温度的函数，而泊松比μ与温度无关。

根据Love壳体理论[7]，壳体微段的几何关系满足：

其中：u，v，w为中面位移；ex，eθ和exθ分别为壳体微段正应变与切应变。

不考虑温度改变的影响，壳体微段的内力和内力矩为：

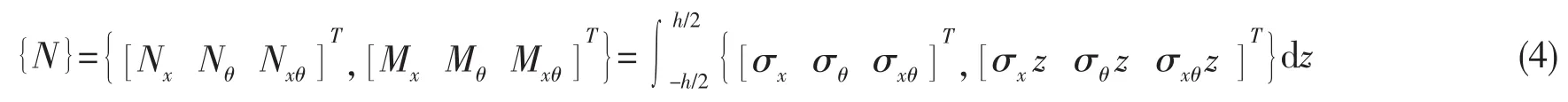
壳体的平面应力状态可表示为：

其中：σx，σθ和σxθ分别为壳体微段的正应力和切应力；且，

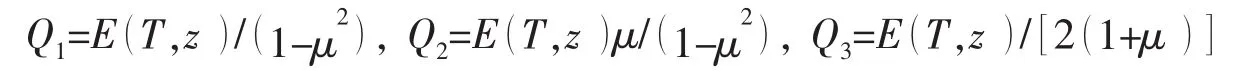
当壳体内外侧温度发生改变时，会在壳体内产生热应力。设温度仅沿厚度方向改变，则相应的热（预）内力为：

其中：△T是温度差，为改变后的壳体温度与初始温度之差。由此，壳体微段内的总内力和总内力矩为

1.2 系统控制方程

假定壳体内外均为轻流体，忽略流体对壳体的声压反作用力。壳体受到温度改变产生的热（预）应力，可得功能梯度材料圆柱壳的自由振动方程如下：

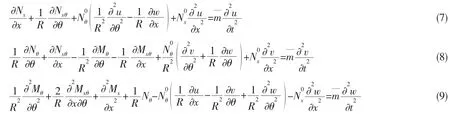
假定温度仅沿厚度方向改变，而在轴向和周向为均匀分布，壳体预变形为轴对称形式，圆柱壳长径比较大且两端为简支边界，可知[8]：

采用波动法[9-10]，设壳体的中面位移模式为：

其中：n为周向模态数，km为轴向波数，ω为圆频率。

将（1）-（6）式、（10）式和（11）式代入（7）-（9）式，合并化简可得：

式中：λ＝kmnR为无量纲波数；f为频率；Ai，Bi，Ci分别为拉伸刚度，耦合刚度以及弯曲刚度，可定义如下：

由于不考虑壳体周围轻流体的影响，壳体的频散特征方程是关于λ的八次多项式方程，其解可以分为三类：当λ为实数时，表示沿壳体轴向的传播波；当λ为虚数时，表示沿壳体轴向的近场衰减波；而当λ为一对共轭复数时，表示一对沿相反方向传播的共轭衰减波。

为了研究温度效应对壳体自由振动时各运动分量的影响，可由（12）式得壳体振动波各运动分量之比为：比值较小说明径向运动占的成分较大，比值较大则说明轴向运动或周向运动所占的成分较大。

2 数值结果与讨论

定义功能梯度圆柱壳内层材料为不锈钢，外层材料为氧化锆，材料参数见表1，泊松比μ=0.3。壳厚径比h/R=0.02。

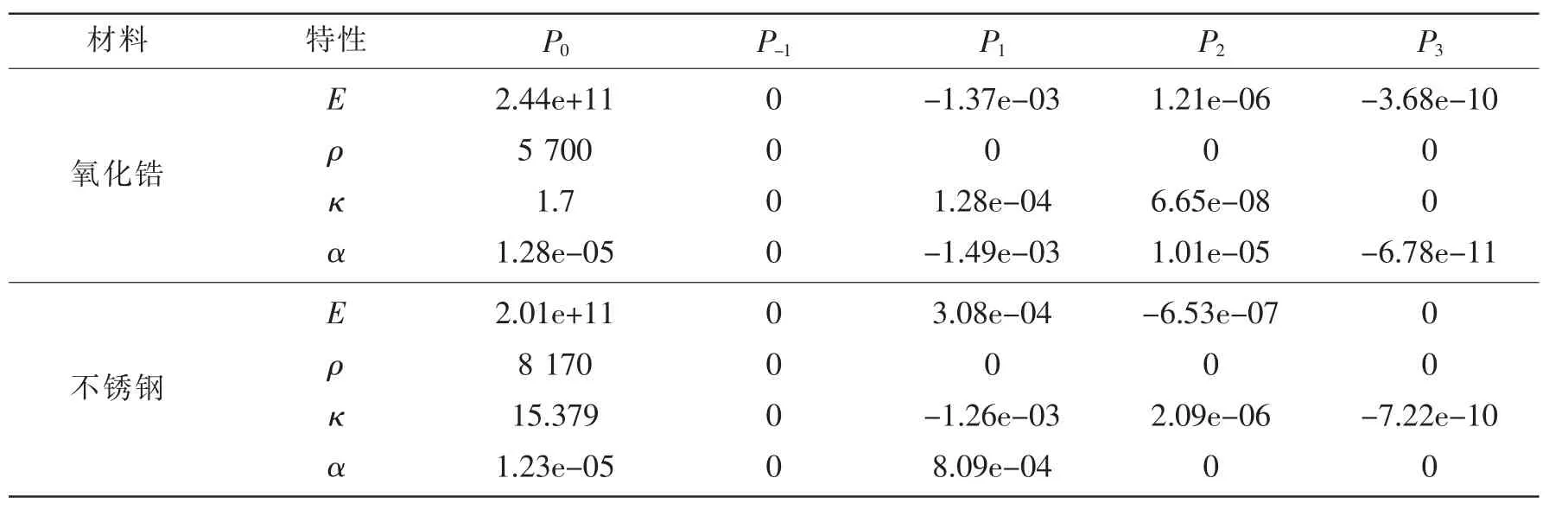
表1 功能梯度圆柱壳组成材料的特性Tab.1 The material properties of FG cylindrical shells

考虑两种温度分布方式：

（1）TD1，沿厚度方向均匀升温。假定初始状态壳体温度为T1，升温后为T2，令T（z）=T2，△T=T（z）-T1=T2-T1。

（2）TD2，沿厚度方向温度分布满足稳态一维热传导条件，假定初始状态壳体温度为T1，升温后壳体外侧温度为T2，内侧温度保持不变，即[3]：

将上式按级数展开，合并简化后可得：

为了验证本文理论和方法的正确性，按照文献[1]的参数计算温度为300 K时的功能梯度材料壳体固有频率，结果如表2所示。其中m表示壳体轴向半波数。

分别计算TD1和TD2时，对应频率的振动波无量纲波数，研究温度对功能梯度材料壳体频散特性的影响。按照文献[11]的方法，计算在本文所取的壳体材料参数和边界条件下，均匀升温后的壳体屈曲温度。如图3所示，壳体厚径比为0.02时，不同体积分数指数对应的屈曲温度。分析图2可知，一般情况下，T1和T2都相同时，TD1与TD2相比，升温后壳体厚度方向各位置的温度，TD1均高于TD2。由（6）式可知，温度改变越大，壳体内热应力越高，屈曲温度就越低。因此TD1的屈曲温度要低于TD2。为了避免壳体由于热应力产生屈曲，在讨论温度对频散特性的影响时，壳体升温不应超过当前的屈曲温度。由此可知，只要保证壳体升温低于图3所示的屈曲温度，在计算TD1和TD2下的频散特性时，即可不考虑热应力带来的稳定性问题。本文在计算过程中，取功能梯度材料体积分数指数N=1。

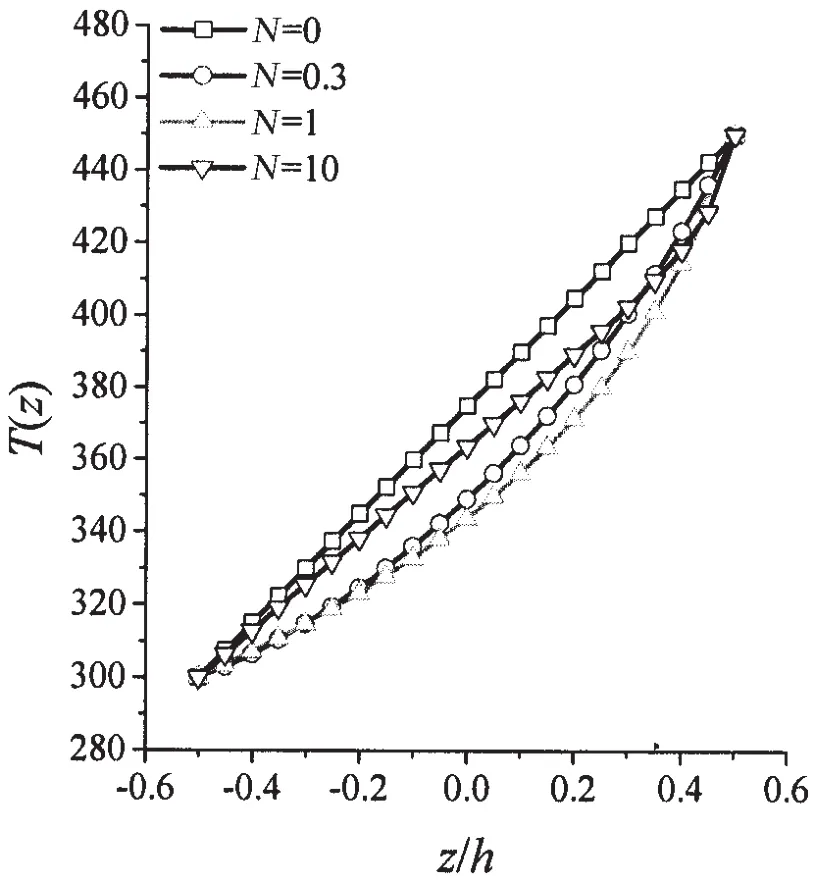
图2 TD2温度沿厚度方向分布Fig.2 The temperature distribution through the thickness of TD2

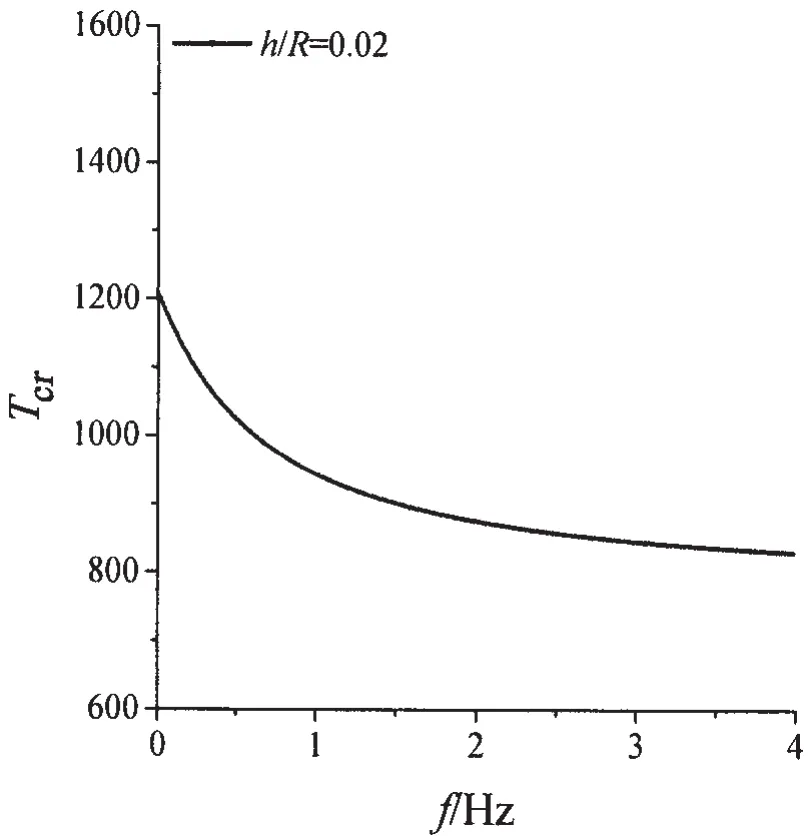
图3 屈曲温度与体积分数指数的关系Fig.3 The relationship between the buckling temperature and exponent of volume fraction

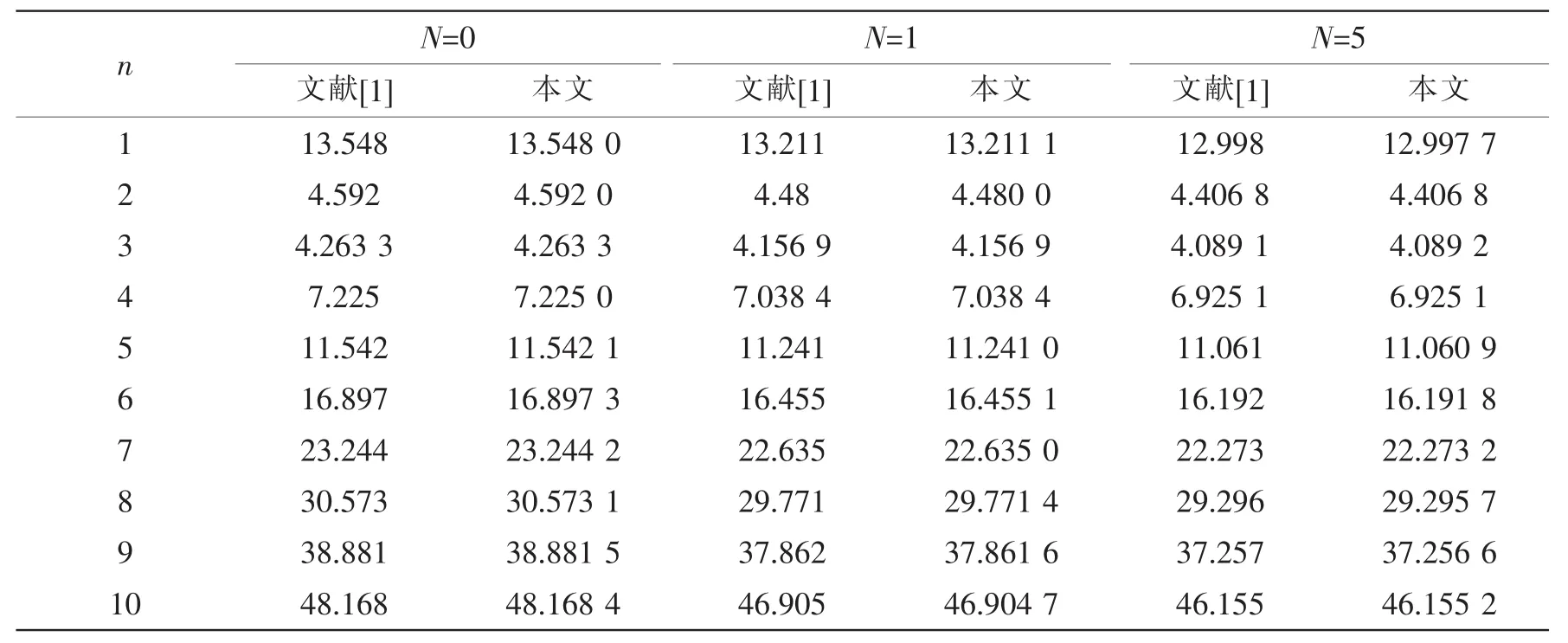
表2 功能梯度圆柱壳固有频率比较（m=1，h/R=0.002，L/R=20）Tab.2 The natural frequency comparison of FG cylindrical shells(m=1,h/R=0.002,L/R=20)

图4表示功能梯度壳体在自由状态（取300 K）下均匀升温至450 K后，结构内振动波的频散特性。实线表示传播波，虚线为共轭衰减波，点线为近场衰减波（下同）。图5以n=1为例，给出了传播波以及近场衰减波各运动分量之间的关系。结合图4和图5可推得，各周向模态下，R1波主要以轴向拉伸运动为主，R2波主要以周向扭转运动为主，R3波和I1波主要以径向弯曲运动为主。随着周向模态数的增大，各支传播波的截止频率不断提高。

当温度沿厚度方向均匀升高时，各支传播波的频散曲线上移，轴向波数增大。以弯曲运动为主的R3波，受温度的影响较为明显。而分别以拉伸运动和扭转运动为主的R1波和R2波受温度的影响较小。由此可知，在一定的轴向波数下，随着温度的升高，壳体径向振动固有频率有较明显的降低，而轴向振动和周向振动的固有频率受温度的影响较小。

共轭衰减波在一定的频率之后转化为近场衰减波，随着周向模态数的增大，共轭衰减波和近场衰减波的个数增加，共轭衰减波向近场衰减波转化的频率也随之增高。当温度升高时，I1波轴向波数减小。在I1波出现初期的频段内，受温度的影响较为明显，随着频率的增大，温度对I1波的影响逐渐减弱。当温度升高时，共轭衰减波向近场衰减波转化的频率也有所提高。随着周向模态数的增大，温度改变前后转化频率之间的差距也逐渐增加。I1波以外的近场衰减波受温度的影响较小。

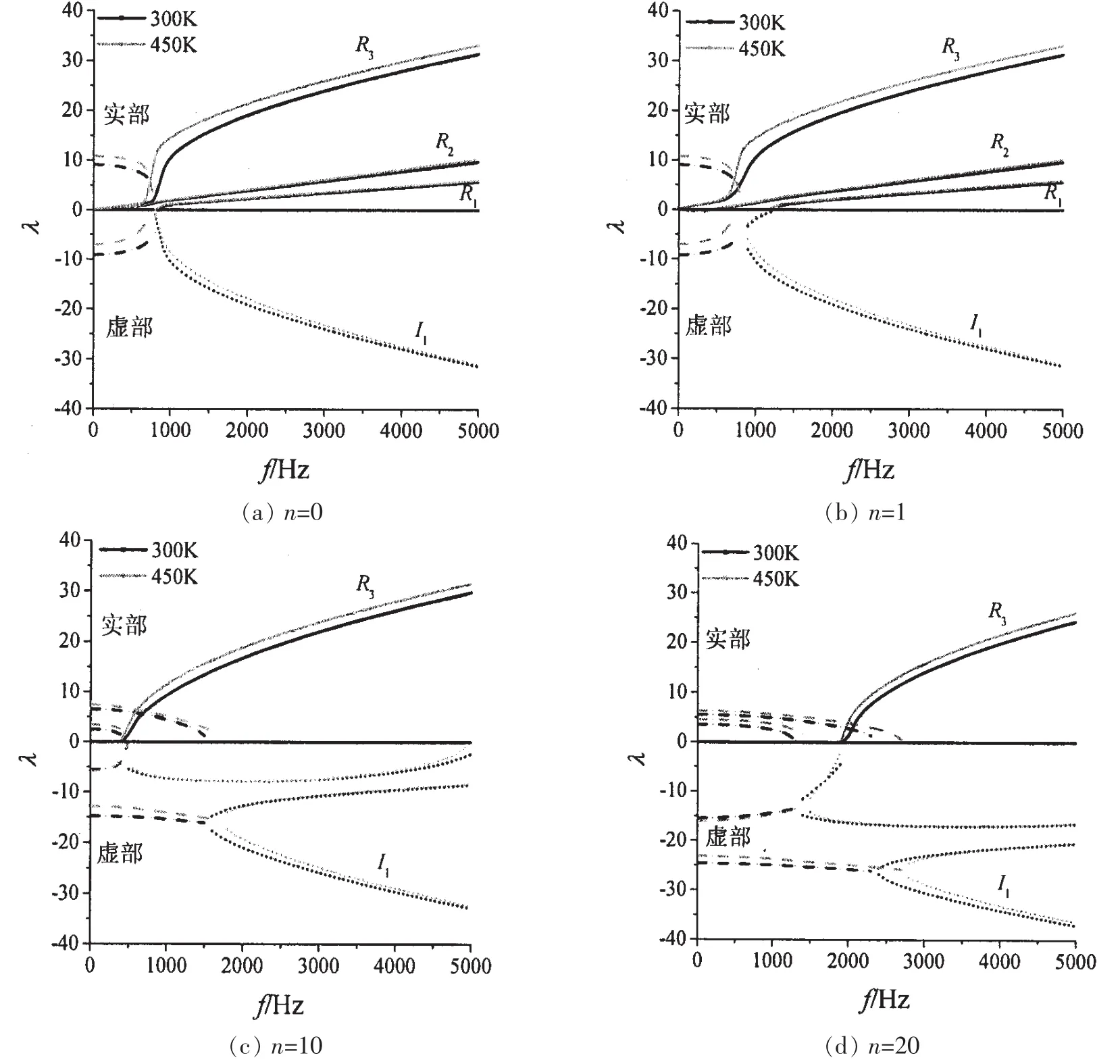
图4 TD1时温度效应对功能梯度圆柱壳频散特性的影响Fig.4 The thermal effect on dispersive characteristics in TD1

图5 自由状态下各支振动波运动分量比（n=1）Fig.5 Motion components radio of vibration wave in free state(n=1)

现比较TD2温度分布与TD1温度分布方式对壳体频散特性的影响。设TD2时，功能梯度壳体外侧升温至450 K，而内侧温度保持不变。如图6所示，两种温度场下，频散曲线的整体趋势相似，TD1时各支传播波的轴向波数高于TD2，其中R3波轴向波数的差距较为明显，随着频率的增大差距逐渐减小。TD1时，共轭衰减波向近场衰减波转化的频率高于TD2，且随着周向模态数的增加，差距增大。两种温度分布方式下，I1波之外的其余近场衰减波频散曲线相差较小，基本重合。结合图4结果可知，与自由状态相比，当壳体外侧温度相同时，TD2温度分布对频散的影响小于TD1。

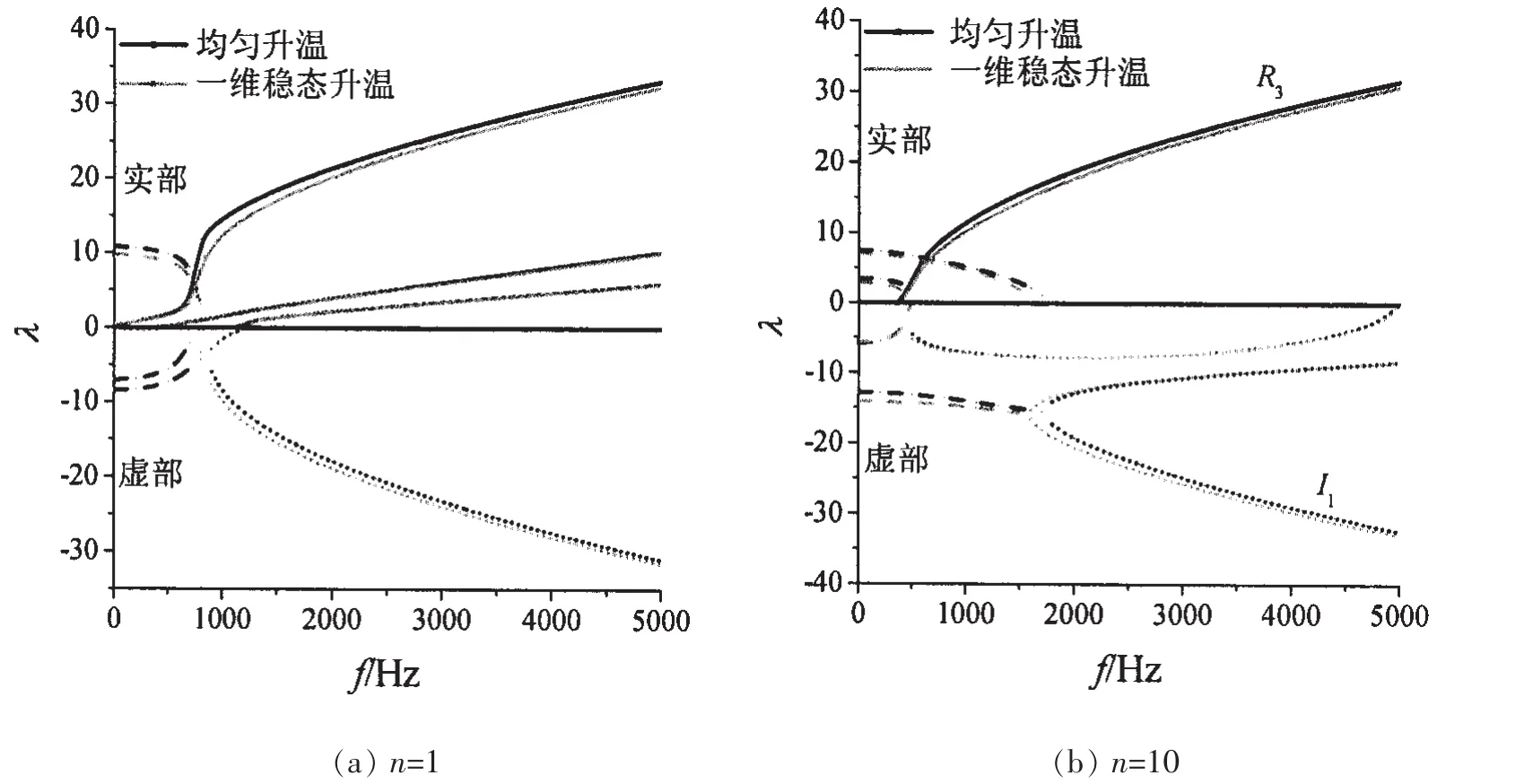
图6 不同温度分布方式对功能梯度壳体频散特性的影响Fig.6 The difference of the influence on dispersive characteristics between the TD1and TD2

由图2可知，体积分数指数变化会改变TD2温度场沿厚度方向的温度分布，由（6）式可得，这将使预内力发生变化并由此影响壳体的固有振动特性。

以n=1时传播波R3和近场衰减波I1为例，研究TD2温度场下，体积分数指数改变对振动波频散特性的影响。

如图7所示，可知在TD2温度分布下，体积分数指数的改变对壳体频散特性的影响较小。

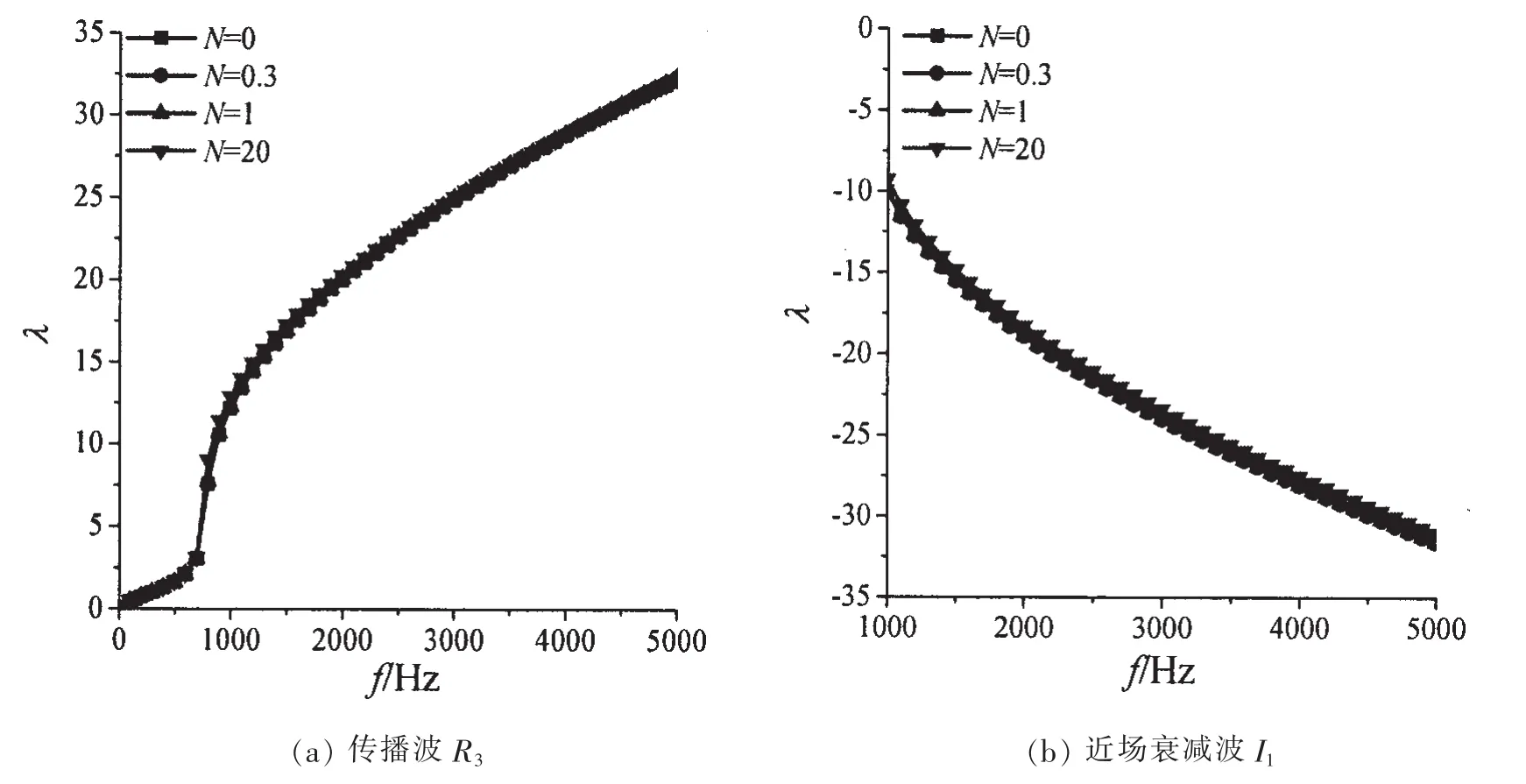
图7 TD2温度分布下体积分数指数频散特性的影响（n=1）Fig.7 The influence of volume fraction exponent on the dispersive characteristic in TD2(n=1)

3 结论

本文基于经典壳体理论，以不锈钢和氧化锆复合而成的功能梯度材料圆柱壳为例，研究了热环境下功能梯度圆柱壳的频散特性，并比较了不同温度场对频散的影响。当温度沿厚度方向改变后，功能梯度壳体的宏观材料特性沿径向发生变化，并使壳体受到热（预）内力作用，表现为在壳体自由振动方程中加入了热（预）内力项，最终导致壳体波传播特性的改变。

在不同温度场作用下，以径向运动为主的振动波受温度影响较大。共轭衰减波向近场衰减波转化的频率随着温度的升高而增大。沿厚度均匀升温与非均匀升温相比，当壳体最大温升相同时，壳体频散特性相似，且前者对频散的影响高于后者。功能梯度材料的体积分数指数会对非均匀温度场沿壳体厚度方向的温度分布产生影响，而对壳体频散特性的影响较小。

[1]Loy C T,Lam K Y,Reddy J N.Vibration of functionally graded cylindrical shells[J].International Journal Mechanical Sciences,1990,41(3):309-324.

[2]Kadoli R,Ganesan N.Buckling and free vibration analysis of functionally graded cylindrical shells subjected to a temperature-specified boundary condition[J].Journal of Sound and Vibration,2006,289(3):450-480.

[3]Haddadpour H,Mahmoudkhami S.Free vibration analysis of functionally graded cylindrical shells including thermal effects[J].Thin-Walled Structure,2007,45(6):591-599.

[4]Scott J F M.The free modes of propagation of an infinite fluid-loaded thin cylindrical shell[J].J Sound Vib,1998,125(2): 241-280.

[5]Schenck H A.The efficient calculation and display of dispersion curves for a thin cylindrical shell immered in a fluid[C]// Proc.ICA,Paper B8-2,1992.Beijing,China,1992.

[6]Guo Y P.Approximate solutions of the dispersion equation for fluid-loaded cylindrical shells[J].J Acout.Soc.Am.,1994, 95(3):1435-1440.

[7]Love A E H.A treatise on the mathematical theory of elasticity[M].4th ed.Cambridge:Cambridge University Press,1952.

[8]Eslami M R,Javaheri R.Buckling of composite cylindrical shells under mechanical and thermal loads[J].Journal of Thermal Stresses,1999,22(6):527-545.

[9]Zhang X M,Liu G R,Lam K Y.Vibration analysis of thin cylindrical shells using wave propagation approach[J].J Sound Vib,2001,239(3):397-403.

[10]Zhang X M,Liu G R,Lam K Y.Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach[J].Applied Acoustics,2001,62(3):229-243.

[11]Wu Lanhe,Jiang Zhiqing,Liu Jun.Thermoelastic stability of functionally graded cylindrical shells[J].Composite Structures,2005,70(1):60-68.

Dispersion characteristics of functionally graded material cylindrical shells in the thermal environment

YE Xi1,SUN Yong-hua1,LIU Jian-hua1,YAO Xiong-liang2
(1 Marine Design&Research Institute of China,Shanghai 200011,China;2 College of Shipbuilding Engineering, Harbin Engineering University,Harbin 150001,China)

The research about wave-motion characteristics of functionally graded material structure in the thermal environment was presented.Based on the classical shell theory,the free vibration equations of functionally graded cylindrical shells in the different temperature fields were deduced.The results show that the thermal effect is obvious on the propagation wave whose main motion component is bending.The thermal effect on the near-field decaying wave is reduced with the increment of the frequency.The conversion frequency from conjugate decaying waves to near-field decaying waves is increased with the increment of the temperature.Compared with the nonlinear temperature distribution through the thickness which meets the 1-D thermal conduction condition,as the same maximum temperature rise,the thermal effect of uniform temperature rise on the dispersion characteristics is more obvious.The results in this paper could provide reference for the research about wave-motion characteristics of functionally graded material in the thermal environment.

cylindrical shell;functionally graded material;dispersion characteristics;thermal effect; exponent of volume fraction

O343.2

A

10.3969/j.issn.1007-7294.2015.04.009

1007-7294（2015）04-0411-09

2014-11-16

国家自然科学基金重点项目（50939002）；国家自然科学基金青年基金（11402143）

叶曦（1987-），男，博士，E-mail:yexi0527@163.com；孙永华（1968-），男，研究员。