水下加肋双层圆柱壳体的振—声传递路径分析
2015-04-25张磊曹跃云杨自春何元安
张磊,曹跃云,杨自春,何元安
(1海军工程大学动力工程学院,武汉430033;2中国船舶工业集团公司船舶系统工程部,北京100036)
水下加肋双层圆柱壳体的振—声传递路径分析
张磊1,曹跃云1,杨自春1,何元安2
(1海军工程大学动力工程学院,武汉430033;2中国船舶工业集团公司船舶系统工程部,北京100036)
简要介绍了有限元声振耦合和结构振-声传递路径分析(TPA)的基本理论。基于CAE技术建立了TPA模型,通过ANSYS声振耦合的谐响应分析,获得水下双层圆柱壳体振动响应和声场中的声压响应,利用矩阵条件数曲线优选测点位置,并结合奇异值修正的方法改善频响函数矩阵病态问题,求得振源的耦合激励力和振—声频响函数。由自编TPA程序计算得到两个振源作用下目标点的合成噪声响应与ANSYS实际计算吻合很好。利用频谱贡献云图、矢量叠加图及数据对比的方式分析了传递路径对壳外目标点噪声的贡献,从传递路径的角度找出了对壳外噪声起主导作用的环节。可见,基于CAE方法的水下双层圆柱壳体结构振-声TPA方法具有精度高、易操作、成本低等优点,对潜艇的优化设计、运行管理、针对性的维修均具有十分重要的意义。
传递路径分析;振—声;有限元;双层圆柱壳体
0 引言
有限长加肋圆柱壳体是潜艇舱段的主要结构形式,潜艇的结构噪声来源于内部机械激励壳体振动并带动周围流体介质产生声辐射,对于这类复杂的系统,主要噪声源的识别、量化和噪声的传播途径识别问题是一项非常重要而又很难的工作[1]。
结构振—声传递路径分析(Transfer path analysis TPA)是辨识主要的激励源和相应传递路径的重要方法,有助于控制结构振动与噪声的传递[2]。结构振-声传递路径分析最初是一项以试验为基础的方法,近年来随着计算机技术的发展,基于CAE完成TPA的仿真,已经可以很大程度上替代真实的试验,或者将试验与CAE技术相结合。结构振-声传递路径分析在国内外的汽车设计领域已有较为成熟的应用[3-4],在其他领域特别对于水下有限长加肋圆柱壳体模型却鲜有研究。水下有限长加肋圆柱壳体模型具有较强的声固耦合特性,若用试验方法对其进行振-声传递路径分析,难度较大、周期较长且成本较高,而基于CAE方法的振-声传递路径分析可以有效地克服上述缺点。因此,如果能采用CAE技术在设计阶段就了解和掌握艇内主要的振动源和各振源的传递路径,并在此基础上进行艇体结构的声学优化或采取针对性的减振降噪措施,对提高潜艇的抗噪能力具有十分重要的意义。
结构振—声TPA首先需要进行结构的振动和声辐射分析,水下结构振动声学分析方法主要有解析法和数值法两类,解析法使用于简单的结构,对于复杂结构和需要相对精确的解,一般采用数值计算法,有限元方法就是一种广泛应用的数值求解法,利用大型通用有限元软件ANSYS进行结构的声振耦合分析已被证明是可行的[5]。本文通过ANSYS声振耦合的谐响应分析,获得水下双层圆柱壳上的振动信号和声场中的声压信号,结合矩阵条件数曲线的诊断和奇异值的修正方法,求得振源的耦合激励力和振-声频率响应函数。最后,通过matlab软件自编TPA程序计算得到两个振源作用下目标点的噪声响应、各条传递路径的贡献量以及主要的传递路径等。
1 有限元方法计算有限弹性结构振动与声辐射
1.1 基本理论
有限元方法计算结构振动与声场耦合问题时,需要在结构的外部紧贴结构表面建立一个流体结构。用有限元法对模型进行分析是通过对结构本身和流体均进行有限元网格离散,求解波动方程和运动方程来实现的。在流固耦合交界面上,结构振动会产生流体负载,而声压同时对结构产生一个附加力,所以必须同时计算结构动力方程和流体域的波动方程,得到完整的流固耦合问题的有限单元法离散方程

e阵,ρ0为流体介质密度,Ue、Pe为节点的位移和声压向量,Fe为结构的载荷向量。
对(1)式进行求解可以得到结构的振动特性和声压分布。当将流体边界上的声边界阻尼取为全吸收时(即满足远场条件),可近似计算整个流体区域内结构与流体耦合振动和声场问题。
1.2 利用ANSYS进行结构声振耦合计算
本文采用的模型是一有限长、环向加肋的双层圆柱壳,其两端带有半球帽。模型的轴长为L=605mm,内壳肋距为l=89 mm,外壳半径为D=75 mm,内壳半径为d=60 mm,外壳厚度为a=6 mm,内壳厚度为b=12 mm,双层圆柱壳间用托板连接,板厚度为3 mm,板间距为89 mm。结构材料属性:弹性模量E=2.1×1011Pa,泊松比μ=0.3,密度为ρ1=7 800 kg/m3;流体材料属性:声速为c=1 460 m/s,密度为ρ2= 1 000 kg/m3。
建立有限元模型时,内壳和外壳均使用Shell63薄壳单元,环肋使用Beam188中的T型梁单元。流体采用8节点的三维声流体单元fluid30,分为与结构接触和非接触单元,用Fluid130单元来建立三维流体区域的边界,该单元提供了第二级吸收边界条件,使得输出的压力波到达模型的边界以最小的反射吸收到流体域内。这个无线单元对低频和高频激励都执行得很好,数值试验已确定吸收单元远离结构或振源区域以外大约0.2λ放置能产生准确的结果,λ=c/f为压力波的主波长[6],c为流体声速,f为压力波主频率。对于直径为D的球壳,封闭边界半径至少应为D/2+0.2λ,此处取D=L,计算频率范围为30-2 500 Hz,通过分析取水体直径为4 m的球体。内外壳体之间充满水介质,仍采用fluid30单元。在网格划分时,网格必须足够的细致以能分辨最小主频,在流体介质中取最小波长,一个波长范围内有10个单元[6]。结构和流体的有限元模型如图1、2所示。
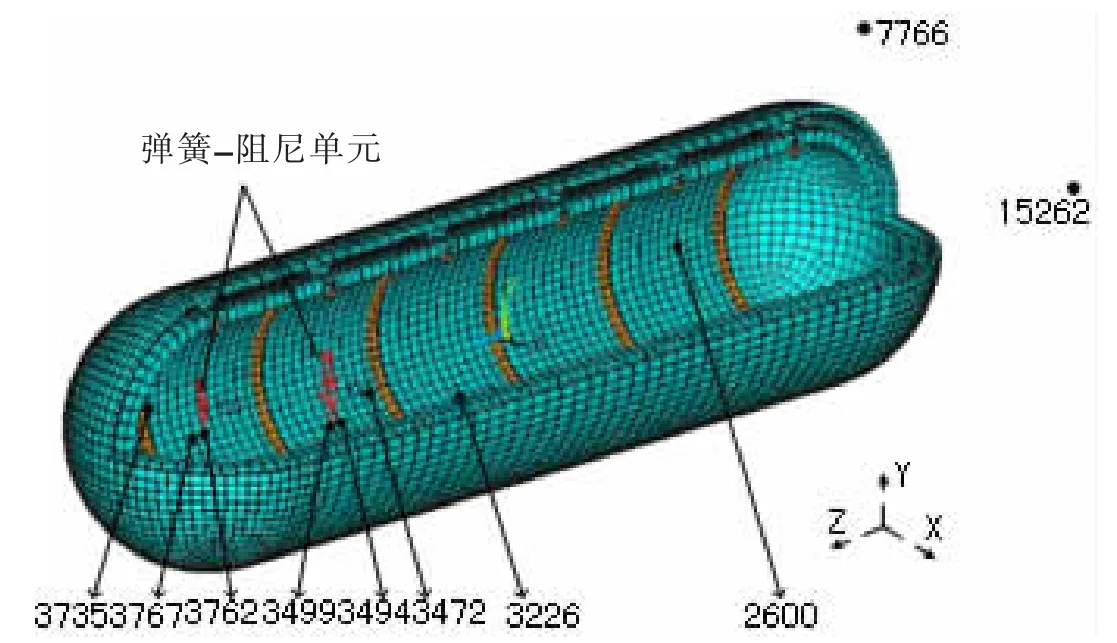
图1 加肋双层圆柱壳体有限元网格Fig.1 The finite element model of cylindrical double-shell
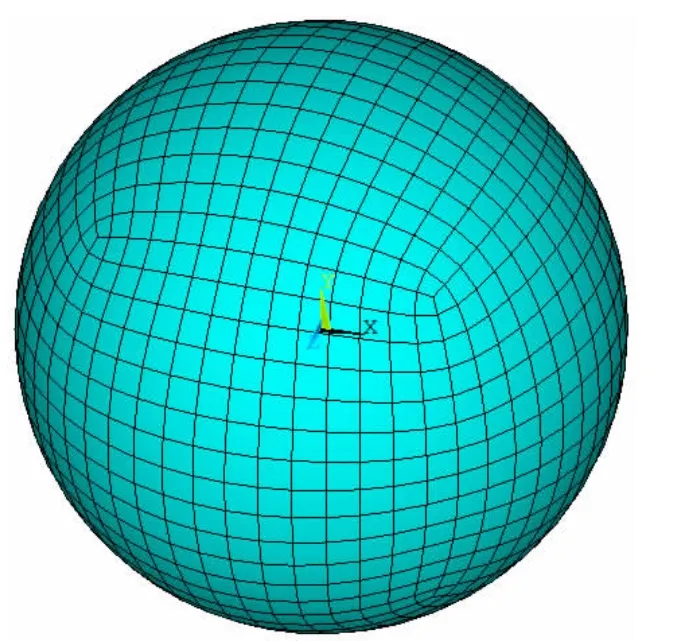
图2 外部流体介质有限元网格Fig.2 The finite element model of fluid medium
为了考虑激励力之间的耦合影响,文中选择两个相距较近的激励力点,进一步模拟振源与壳体之间的作用情况,将激励力分别作用在两个与内壳体相连的弹簧-阻尼单元上,如图1所示。
2 TPA模型的建立
结构振—声传递路径为机械设备产生的振动激励,通过基座的衰减或放大作用,传递到艇体联结点上并表现为力激励,此力再通过艇体传递到各处使得壳体振动从而辐射出噪声。对于某一激励源,如果已知某一路径上的传递函数和工作载荷,该路径对目标位置噪声的贡献量可表示为

式中:Hi′(ω)是传递函数,Fi(ω)为激励力的频谱。如果有n条路径,总响应可以是各路径分量的线性叠加:

式中:Pstru(ω)为目标点上的响应,可以是声压或加速度等,此处选择声压。
传递路径分析(TPA)必须先获得结构噪声各传递路径的传递函数及其工作载荷,工作力的获取方法主要有:直接测量法,复刚度法,矩阵求逆法和驱动点频响函数法等[2],其中后三个为间接法。而获取传递函数的方法主要有直接测量法和基于互易性原理的测量方法[3],本文采用逆矩阵法来求解激励载荷,传递函数为频率响应函数,由直接测量法获得。
对于一线性时不变系统,当有激励F1,F2,…Fn,时,存在响应X1,X2,…,Xm,由系统的运动方程可得

于是载荷力向量可根据下式计算得到:

式中:Fj是路径点j处的工作载荷,也称为路径载荷;Xi是响应点i上的工作响应,在逆矩阵法计算路径点载荷中,把响应点i称为载荷计算参考点,Xi称为参考点信号,也称为参考点响应。[H]m×n为载荷计算的频响函数矩阵;{F}n×1为路径载荷力列向量;{X}m×1为参考点响应信号列向量。从理论上讲,载荷识别似乎很简单,但在实际中,测量噪声及各种信号污染不可避免,为了排除噪声的影响需用平局技术对频响函数进行估计。本文取和的算术平均,得到H3估计。
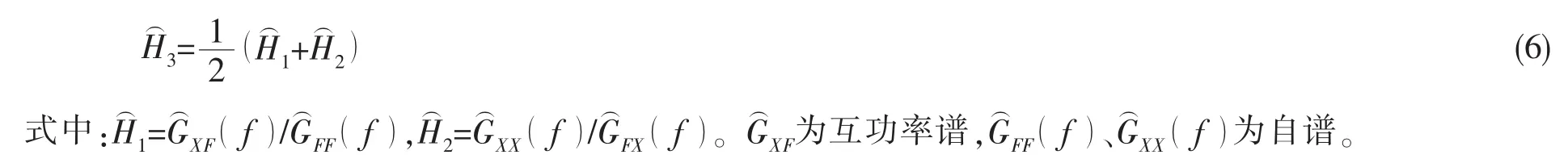
通过求得激励力到参考点加速度响应的频响函数矩阵=[]Hm×n及激励力到壳外目标点声压值的频响函数矩阵H′,并在实际工况下测得壳内参考点的加速度向量后,由(2)式和(5)式求得各路径的噪声贡献,通过(3)式合成可得目标点的总噪声。
3 TPA方法应用实例
3.1 主要振源、目标点与传递路径
在水下加肋双层圆柱壳体模型中,弹簧与内壳体的耦合点处有x、y、z 3个方向自由度,即两个耦合点(节点3762,3499)有6个路径点,在水介质声场中任意选择2个目标点,即圆柱壳侧面节点7766,坐标为(-0.074,0.604,-0.361),端面节点为15262,坐标为(-0.003 43,-0.006 89,-1.460),所以振源到目标点处总共有6×2=12条传递路径,本文以ANSYS声场的谐响应分析为基础,通过ANSYS声振耦合计算(频率范围为30-2 500 Hz)获得双层圆柱壳体上的振动信号和声场中的声压信号,作为求解频响函数和工作力的输入条件。
3.2 频响函数的获取
由TPA的理论可知,要得到路径载荷以及路径载荷对目标点的贡献,计算路径点到目标点和路径点到载荷参考点的频响函数是必须的,频响函数的准确性直接影响到最后结果的准确度。本文由于路径载荷对目标点是以力的形式表示,所以参考点对路径点的频率响应函数是加速度信号对力信号的频率响应函数,计算所需的数据根据ANSYS声振耦合分析得到。
在内壳体上选择参考点的位置,为了抑制噪声,增加工作载荷估计可行度,需要方程(4)满足m>n,通常取m≥2n[4]。为避免参考点的作用效应雷同,参考点位置应不对称,且分散布置。紧挨每个耦合点各取一个,此部位的响应包含动态载荷的信息较丰富。为了减少数据提取的重复次数,本文将参考点选为m=3n,即6个参考点(2600,3226,3472,3494,3735,3767)如图1,自由度数量为3×6=18个。在进行频响函数计算时,在每个耦x、y、z 3个方向分别加载激励,为了减少噪声信号的影响,采用多次激励,用平均的方法来计算频响函数,本文在ANSYS声振耦合计算中每个路径点激励3次进行平均处理,提取并保存每个加速度和目标点的数据,利用估计计算得到路径点到所有参考点和路径点到目标点的频率响应函数。图3给出了激励点3762到目标点15262的传递函数幅值。可知,在中低频率范围3762 z向到目标点的传递函数幅值较大,而在高频时3762 x、y向到目标点的传递函数幅值较3762 z向大,即不同频段各路径点的贡献量也不一样。
3.3 工作载荷的求取
为了计算目标点的声压贡献量,除了获得频响函数以外,还需要得到工作载荷,文中采用逆矩阵法计算结构振动的工作载荷。本文的振源相距较近,由于结构的模态特性,参考点的响应之间存在较强相关性,使得载荷计算的频响函数中包含的结构信息存在着很大的相似性,这将导致频响函数矩阵的病态。所以,对频响函数矩阵求逆会出现不稳定,又由于观测噪声不可避免,将导致工作载荷与其准确值差异很大,结果不可信。由此可知,为了准确地计算频响函数矩阵的逆矩阵,需要选取恰当的参考点组成较为良态的频响函数矩阵,以期准确地求得工作载荷。为了避免构造出病态的矩阵,需首先引入病态矩阵有效的诊断方法。矩阵的条件数是诊断矩阵是否病态的有效方法,根据矩阵条件数的定义,将其推广到长方体矩阵有

其中:σ1是频响函数矩阵H的最大奇异值,σr是H的最小奇异值。由于每一个频率处的频响函数矩阵都对应着一个Condition值,此处根据Condition(ω)曲线对载荷计算矩阵的病态程度进行判断。当Condition(ω)曲线在整个频率范围内都较小时,表示计算矩阵质量较好,得出的计算结果比较好。为了减少ANSYS仿真计算的重复次数且避免构造出严重病态的频响函数矩阵,在最初确定参考点个数时已选择m=3n,即共有参考自由度数k=18。一般分析认为取参考自由度数为路径点数的2倍[8],但这种计算方法不够准确。由图4中k=12时的最佳和最差Condition(ω)曲线以及k=6时的最佳Condition(ω)比较看出,k=12时的最差Condition(ω)曲线的条件数均大于k=6时的条件数,说明虽然参考自由度数是路径点数的2倍,但是构造出的频响函数矩阵质量还不如k=6时的矩阵。所以参考自由度的数目不能简单地以路径点数的2倍为选择依据,本文选择k=12的最佳Condition(ω)曲线对应的参考自由度构造频响函数矩阵。
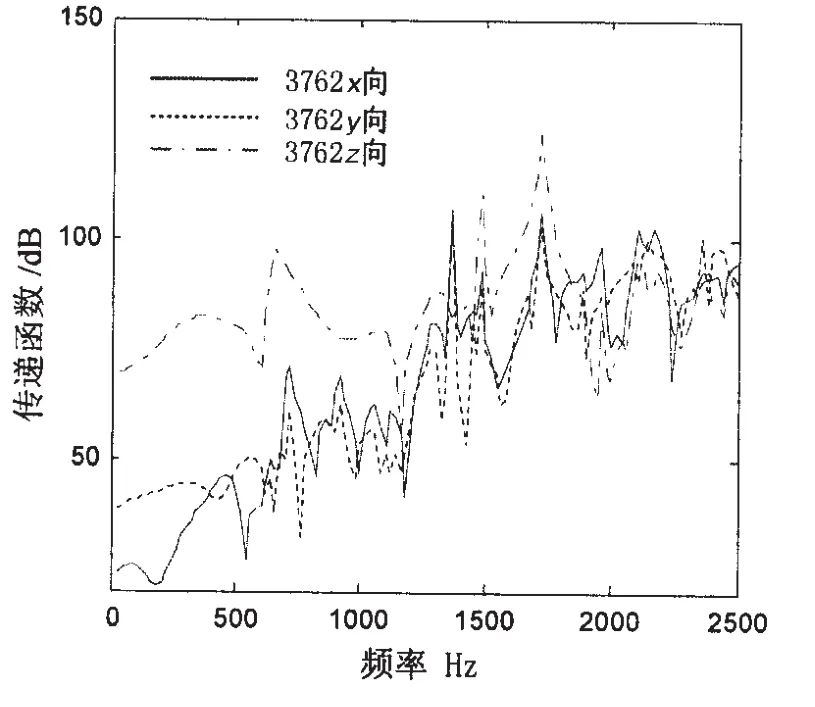
图3 典型传递函数曲线Fig.3 The curve of transfer function

图4 条件数曲线的比较Fig.4 Comparison of condition curve
尽管图4的条件数总体较小,但在个别频率点处的条件数仍然较大,则相应的频响函数矩阵是病态的(此处将Condition>100的矩阵称为病态矩阵)。此时就需要寻求解决病态矩阵求逆问题的方法,此类方法主要有岭估计、截断奇异值及正则化方法等[9]。因截断奇异值的方法易于操作,克服矩阵病态的效果较好而得到广泛的应用,特别是对于呈阶梯型分布的奇异值,用该方法进行修正是合理的,理论上也是严密的。截断奇异值法在处理病态问题的奇异值时是把小的奇异值和对应的特征向量删除,实际上是删掉模型参数中不可靠的部分,以此减小解的方差,但是这样做同时也可能严重地损害了解估计的分辨率,而且对于奇异值均匀下降型分布时,模型参数的可靠成分和不可靠成分的界限不好确定,即截断奇异值的确定很困难。本文将奇异值分成两部分分别进行修正,这种方案兼顾了解的分辨率与方差之间的折中[10]。将设计频响函数矩阵进行奇异值分解得

式中:U和V均为正交矩阵,D=diag(α1,α2,…,αn)为H的奇异值矩阵,降序排列。设t为截断奇异值法保留的最小奇异值门限,即t=αk(k=1,…,n),(α1/αk)2<103<(α1/αk+1)2,q为对应小于t的奇异值个数,用以下公式进行奇异值修正:
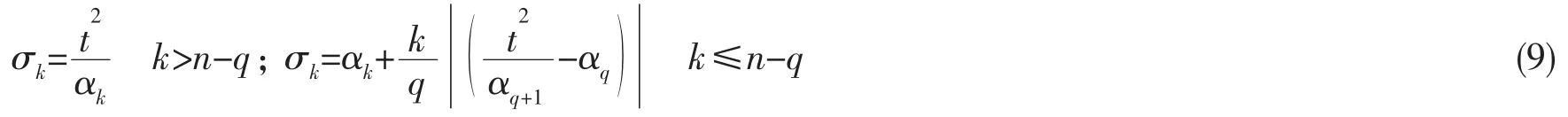
修改后的奇异值为

结合(5)式得到工作载荷的求解表达式为

4 计算数据处理与分析
获得了所有频响函数和工作载荷的数据后,即可对目标点声压贡献量进行合成。本文的载荷工况为在弹簧上同时进行激励,根据ANSYS声振耦合谐响应分析模块计算的振动和声场响应结果,获取在振源作用下参考点加速度信号和目标声压信号,为加肋双层圆柱壳在两个振源下的结构振动—声场的传递路径分析提供数据输入。本文通过MATLAB来编制TPA的程序,参考自由度数取k=12且Condition(ω)曲线为最佳时的组合。将频率点处对应频响函数矩阵的条件数大于100的频响函数矩阵利用3.3中的方法进行修正,以图3中两个较大频率点为例,可知两处频率对应矩阵的条件数均大于200,即矩阵存在较严重的病态,奇异值修正前后目标点7766声压响应值与实际计算值的比较见表1,可以看出,本文采用的奇异值修正方法,最终求得目标点的声压与计算的真实值吻合较好,说明该方法在处理病态频响函数矩阵求逆时有较好的精度。
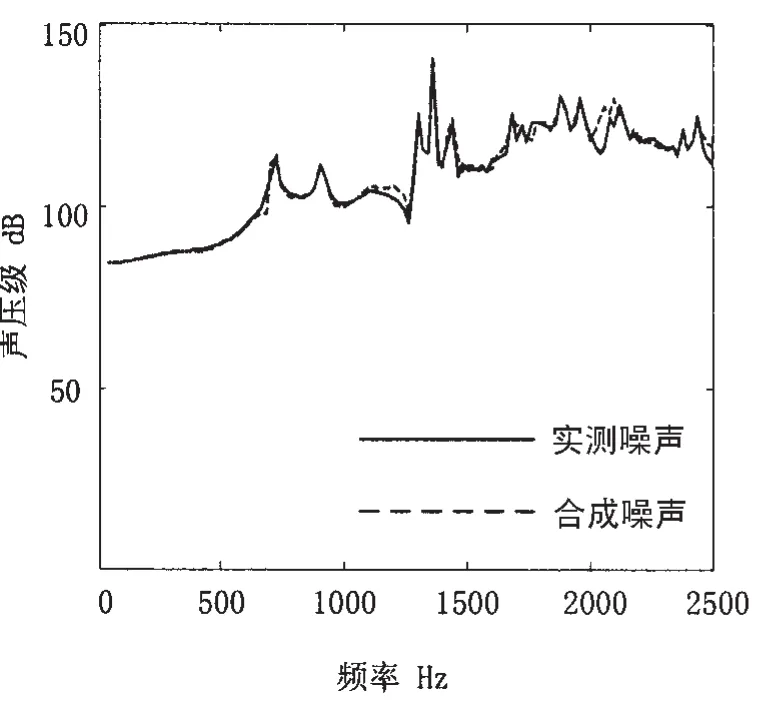
图5 目标点7766的合成与实测噪声比较Fig.5 Contrast of synthesized noise and compute result to node 7766
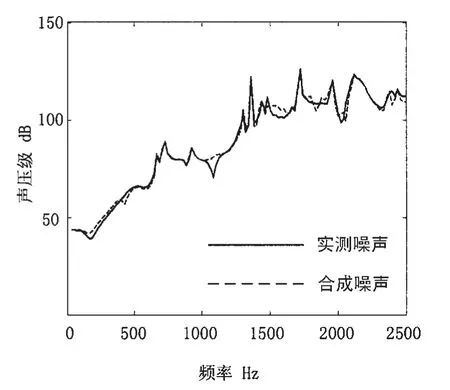
图6 目标点15262的合成与实测噪声比较Fig.6 Contrast of synthesized noise and compute result to node 15262
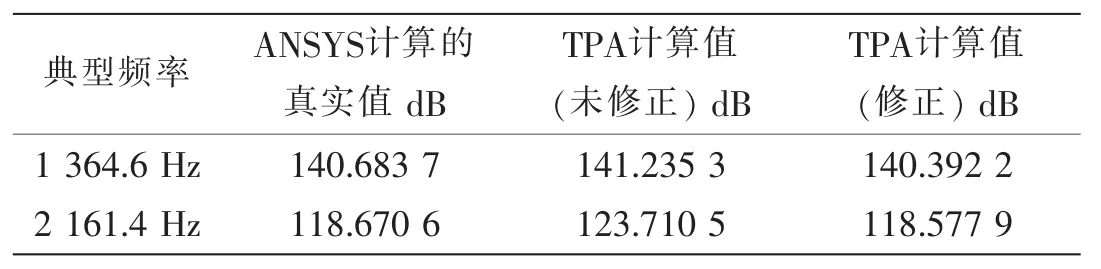
表1 目标点7766典型频率点的声压响应值比较Tab.1 Comparison of pressure response at node 7766
以目标点7766和15262为例,对内壳两个振源到壳外目标点的各条路径贡献量进行合成,并与ANSYS实际计算值所得的壳外目标点的噪声值进行比较,结果如图5、6所示。比较壳外任意两个目标点合成噪声和实际计算噪声发现,两者的变化趋势相同且两者吻合较好,这验证了壳外噪声传递路径模型和ANSYS计算模型的正确性。
图7和图8为各路径对目标点7766和15262噪声的贡献谱图,从图中可以看出:在1 365 Hz左右出现峰值,路径点3762的x和y方向、路径点3499的x和y方向的振动对目标点7766,15262的噪声贡献量均较大。图8在1 723 Hz左右出现出现了峰值,路径点3762的z方向、路径点3499的z方向的振动对目标点15262的噪声贡献量均较大。
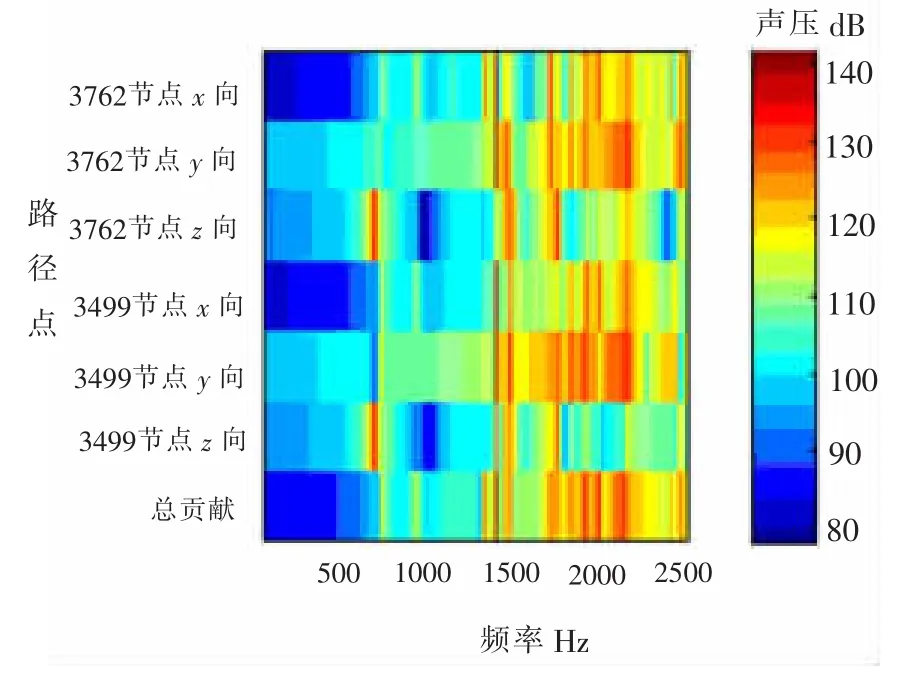
图7 目标点7766各传递路径噪声贡献谱图Fig.7 Contribution of each transfer path to node 7766
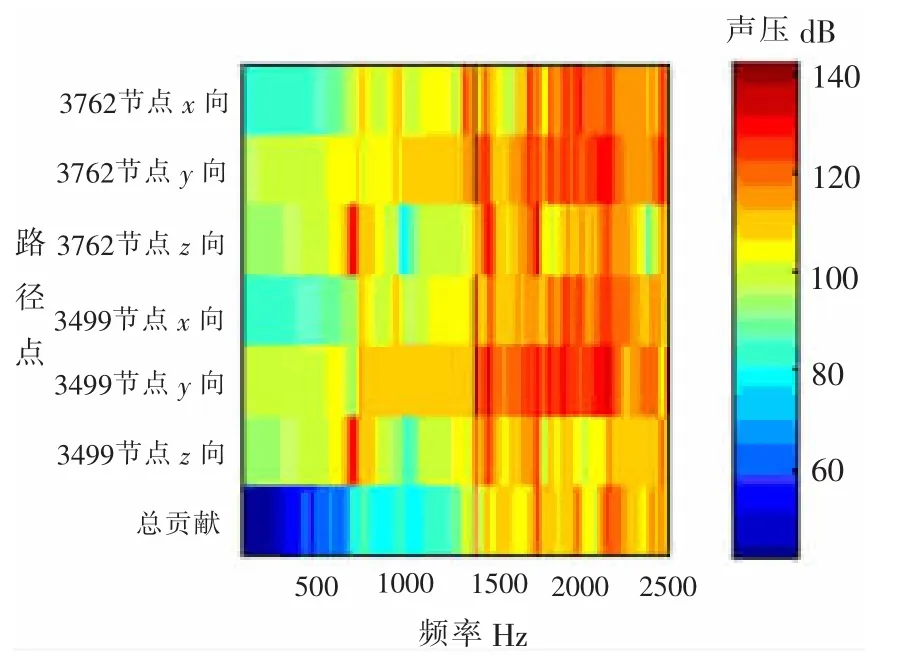
图8 目标点15262各传递路径噪声贡献谱图Fig.8 Contribution of each transfer path to node 15262
利用噪声的贡献谱图分析时值得注意的是,一条具体的传递路径所传递的能量引起的声压贡献与幅值和相位相关,如图7中,在667 Hz左右,路径点3762的z方向、路径点3499的z方向显示有很大的贡献,但是总的贡献量依然很小,这可能是由于不同路径之间的相位反向,使得总的贡献量降低。因此,在进行传递路径分析时,先弄清楚各路径所传递噪声的相位是特别重要的。
图9为1 365 Hz时各条传递路径对目标点15262响应贡献的矢量图,取路径点3762 x向为参考相位。从图中可以看出,这些不同的传递路径贡献矢量的叠加,由于相位不同,有的相互加强,有的相互削弱,最终的响应是矢量相干叠加的结果。在控制壳外振动噪声时,应该特别关注具有较大贡献量的传递路径。从图中可以判定,1 365 Hz时对目标点贡献最大的两条传递路径为路径点3762的x和y方向。
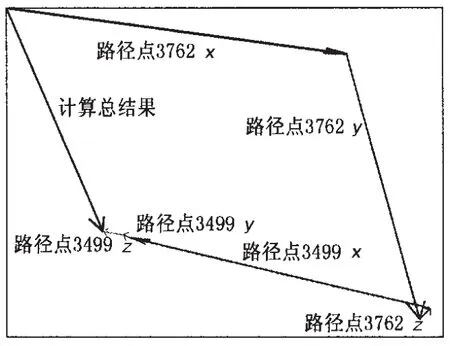
图9 1 365 Hz时各路径贡献矢量叠加图Fig.9 Vector superposition of each transfer path at 1 365 Hz

表2 1 365 Hz各传递路径数据对比分析Tab.2 Related data of each transfer path at 1 365 Hz
通过对壳外噪声贡献量的分析以后,可对壳外噪声主要贡献量的路径进行频响函数与工作力的分析,由此可判断是双层圆柱壳体结构的问题还是噪声源的问题。由表2可知,路径点3762 y向的耦合激励力和振—声传递函数均最大,从而导致了目标点的贡献量最大,3762 x向对目标点的贡献也比较大,这和图9的分析结果一致。虽然路径点3499 x向的振-声传递函数小于路径点3499 y向的传递函数,但其对目标点的贡献量却远大于路径点3499 y向的贡献量,由此可知,路径点3499 x向的耦合激励力是引起其对目标点贡献量大的主要原因。总体分析可知,耦合激励力是决定目标点15262声贡献量大小的主要原因,因此,减少传递路径的声贡献量时应从减小耦合激励力角度考虑。
5 结论
基于CAE技术建立了水下双层加肋圆柱壳体的结构振-声传递路径分析模型,利用ANSYS声振耦合的谐响应分析,结合估计求得频响函数和耦合激励力。选取了参考自由度数k=12且Condition(ω)曲线为最佳时的组合,从而构造出较为良态的频响函数矩阵。针对个别频率点对应的频响函数矩阵条件数较大会导致矩阵求逆误差的问题,文中将奇异值分成两部分分别进行修正,结果表明该方法有较高的精度,最终得到耦合激励力的计算公式。
利用matlab软件自编TPA程序计算得到了两个振源同时作用下壳外目标点由结构振动传递的合成声,与实际计算结果吻合较好,验证了壳外噪声传递路径模型和ANSYS计算模型的正确性。利用频谱贡献云图分析了各条结构传递路径对壳外噪声的贡献,并采用矢量叠加及数据对比的方式详细分析了1 365 Hz时各条传递路径对目标点15262噪声的贡献。结果表明:对目标点影响最大的两条传递路径为路径点3762的x和y方向,路径点3762 y向的耦合激励力和振-声传递函数均最大,从而导致了目标点的贡献量最大。耦合激励力是决定目标点15262声贡献量大小的主要原因,因此,减少传递路径的声贡献量时应从减小耦合激励力角度考虑。
可见,本文基于CAE方法的水下双层圆柱壳体结构振-声TPA方法具有效率高、精度好、成本低等优点,可以在一定程度上替代试验分析方法。该方法能有效地进行潜艇机械设备噪声源的识别、量化和噪声的传播途径识别,进而进行艇体结构的声学优化或采取针对性的减振降噪措施。因此,基于CAE技术的振-声TPA方法对潜艇的优化设计、运行管理和针对性的维修均具有十分重要意义。
[1]何元安,杨德森.水下结构辐射噪声估算方法实验研究[J].船舶力学,1999,3(2):58-62. He Yuanan,Yang Desen.Experiment study of predicting method for radiating noise by submerged vibrating structure[J]. Journal of Ship Mechanics,1999,3(2):58-62.(in Chinese)
[2]Knapen P L.Transfer path analysis related to booming,performed on a car[D].The Netherlands:Eindhoven University of Technology,2006:1-12.
[3]Kim S J,Lee S K.Prediction of interior noise by excitation force of the powertrain based on hybrid transfer path analysis [J].International Journal of Automotive Technology,2008(9):577-583.
[4]王万英,靳晓雄,彭为,等.轮胎振动噪声结构传递路径分析[J].振动与冲击,2010,6(29):88-92. Wang Wanying,Jin Xiaoxiong,Peng Wei,et al.Structural transfer path analysis of tire vibration and noise[J].Journal of Vibration and Shock,2010,6(29):88-92.(in Chinese)
[5]王晶,商德江.利用ANSYSV5.5计算水下弹性结构振动声辐射[J].海洋技术,2003(3):71-73. Wang Jing,Shang Dejiang.The calculation of vibroacoustic problems by ANSYS V5.5[J].Ocean Technology,2003(3): 71-73.(in Chinese)
[6]Khan M S,Cai C,Hung K C.Acoustics field and active structural acoustic control model in ANSYS[C].International ANSYS Conference Proceeding,2002:1-16.
[7]曹树谦,张文德,萧龙翔.振动结构模态分析—理论、实验与应用[M].天津大学出版社,2001:96.
[8]Inoue A,Singh R,Fernandes G A.Absolute and relative path measures in a discrete system by using two analytical methods[J].Journal of Sound and Vibration,2008(313):696-722.
[9]Choi H G,Thite A N.Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination[J].Journal of Sound and Vibration,2007(304):894-917.
[10]王振杰,欧吉坤.一种新的病态问题奇异值修正方案及其在大地测量中的应用[J].自然科学进展,2004,14(6):672-676. Wang Zhenjie,Ou Jikun.A new SVD modified strategy of ill-condition problem using to geodesy[J].Progress in Natural Science,2004,14(6):672-676.(in Chinese)
Vibration-acoustic transfer path analysis of a submerged cylindrical double-shell
ZHANG Lei1,CAO Yue-yun1,YANG Zi-chun1,HE Yuan-an2
(1 Power Engineering college,Naval University of Engineering,Wuhan 430033,China; 2 Institute of Shipbuilding System Engineering,Beijing 100036,China)
Basic theory of vibration-acoustic coupling of finite element method and structural transfer path analysis(TPA)were described and a TPA model was established based on CAE technology.Vibration response of a submerged cylindrical double-shell and pressure response in the acoustic field were acquired by the harmonic response analysis of vibration-acoustic coupling of ANSYS.With the optimal position of reference points is selected by the curve of matrix condition number and the modified singular value method was used to improve the ill-posed problem of FRF matrix,the coupled excitation force and vibration-acoustic FRF were obtained.The results of target response under the action of two vibration sources are calculated by TPA program,which are in good agreement with the results computed by ANSYS.The sound contribution of each transfer path to external noise of the cylindrical double-shell is analyzed by using spectral contribution nephogram and vector superposition chart.The multiple transfer paths which play a leading role in external noise are finally determined.The results indicate that the vibration-acoustic TPA method of the submerged cylindrical double-shell based on CAE technology have high efficiency,good accuracy,etc,which is of great significance in optimization of submarine design,operation management and targeted repair.
Transfer Path Analysis(TPA);vibration-acoustic;finite element method; cylindrical double-shell
TB532U661.44
A
10.3969/j.issn.1007-7294.2015.04.015
1007-7294(2015)04-0462-08
2014-12-25
总装十二五预研基金资助
张磊(1986-),男,博士,E-mail:zhang_lei_21@163.com;曹跃云(1963-),男,教授,博士生导师。
