磁悬浮主被动混合隔振器静稳定性分析

倪 圆，何 琳，帅长庚，李 彦

（1海军工程大学 振动与噪声研究所，武汉 430033；2船舶振动噪声重点实验室，武汉430033）

磁悬浮主被动混合隔振器静稳定性分析

倪 圆1，2，何 琳1，2，帅长庚1，2，李 彦1，2

（1海军工程大学 振动与噪声研究所，武汉 430033；2船舶振动噪声重点实验室，武汉430033）

磁悬浮主被动混合隔振器是一种正负刚度并联的弹性结构。针对该结构存在的稳定性问题，建立了某型磁悬浮主被动混合隔振器的刚度模型。基于虚功原理，推导出判定弹性系统静稳定性的刚度准则。运用该准则，结合混合隔振器的刚度模型分析了该主被动混合隔振器的静稳定性。理论和实验结果表明，该混合隔振器在工作位移内，系统刚度为正，混合隔振器是静稳定的。

磁悬浮作动器；气囊；混合隔振器；静稳定性

0 引 言

主被动混合隔振由被动隔振器承载设备重量并隔离宽频振动，同时利用作动器进行主动控制从而衰减线谱振动，可同时获得良好的宽频隔振效果和线谱控制效果[1]。气囊隔振器具有固有频率低、承载能力大、驻波频率高、无蠕变等特点，是一种性能优异的隔振器。磁悬浮作动器具有无接触、输出力大、等效刚度低的优点，非常适用于主动控制。本文将磁悬浮作动器并联集成到气囊隔振器内部组成主被动混合隔振器，由气囊承载设备重量并高效隔离宽频振动，同时控制磁悬浮作动器消除残余的低频线谱振动，该技术具有可靠性高和功耗小等优点，可以兼顾低频线谱振动控制和宽频振动隔离[2]。

在不进行主动控制时，混合隔振器中气囊在载荷作用下发生变形，其承载能力随盖板位移增加而增大，隔振器刚度为正；磁悬浮作动器的偏置吸引力随盖板位移的增加而增大，与气囊并联后造成系统承载减小，磁悬浮作动器的等效位移刚度为负。磁悬浮主被动混合隔振器可以看做正负刚度并联的弹性结构。正负刚度并联的隔振器能降低系统固有频率，具有较好的低频隔振效果，国内外学者对此进行了大量研究[3-6]，但过低的固有频率或刚度也会使隔振装置的稳定性下降[7]。当隔振器处于负刚度状态时，此时隔振器载荷随位移增大而减小，若以不变的载荷作用于其上，则会发生跳跃现象，造成系统静态失稳[8]。任何隔振器必须是静态稳定的，因此采用磁悬浮主被动混合隔振器进行隔振时有必要分析其静稳定性。

本文基于磁路欧姆定律及实验修正的方法建立了某型磁悬浮作动器的等效负刚度模型，结合气囊隔振器的刚度模型，建立了混合隔振器的系统刚度模型。随后基于虚功原理，推导了弹性系统静稳定性的刚度准则，并根据该准则分析了该混合隔振系统的静稳定性，最后通过实验验证了该稳定性。

1 磁悬浮主被动混合隔振器模型

1.1 主被动混合隔振器结构

本文采用的磁悬浮主被动混合隔振器，是将磁悬浮作动器集成到气囊隔振器内部实现并联安装，系统结构如图1所示。图中气囊上盖板与作动器衔铁连接，气囊下盖板与基座相连。载荷和外界扰动作用于气囊上盖板，气囊隔振器承载设备重量并高效隔离宽频振动向基座传递，同时磁悬浮作动器通过输出磁悬浮力抵消设备传递到基座上的低频线谱振动。系统中气囊刚度为正，磁悬浮作动器永磁偏置产生的等效位移刚度为负。该混合隔振器为典型的正负刚度并联结构。

1.2 气囊刚度模型

气囊隔振器的支撑、弹性作用主要取决于气囊内的压缩气体，气囊壁对隔振器承载力和刚度影响较小。忽略囊壁对隔振器承载力的影响，气囊隔振器的刚度为[9]：

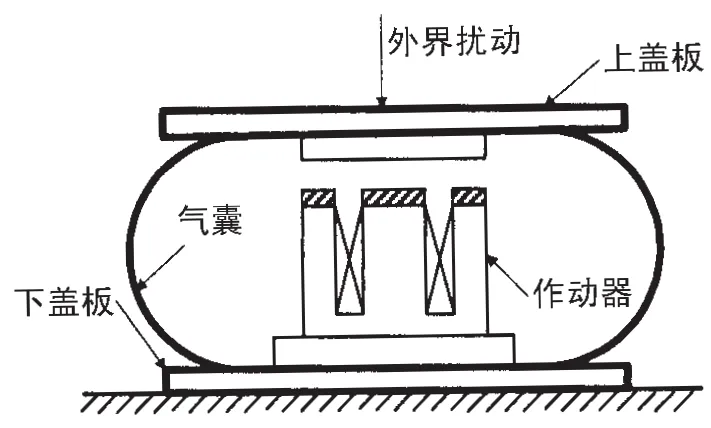
图1 主被动混合隔振系统简图Fig.1 Sketch of active-passive hybrid isolation system

其中：P为囊内气体压力，Se是气囊的有效面积，n为气体多变指数，静态加载时取1。Pa为大气压力，V为气囊体积，z为气囊上盖板位移，取向下位移为正。在气囊额定载荷时位移z为零。对于回转型气囊，气囊隔振器的有效面积可表达为：

囊内气体体积的表达式为：

气囊压力的表达式为：于P，Se和V都是气囊盖板位移z的函数，因此对于固定质量的气体，气囊隔振器的刚度随位移呈复杂的非线性变化关系。以某型气囊隔振器为例，根据气囊刚度模型，代入气囊参数，可得到气囊隔振器刚度随位移变化如图2所示。

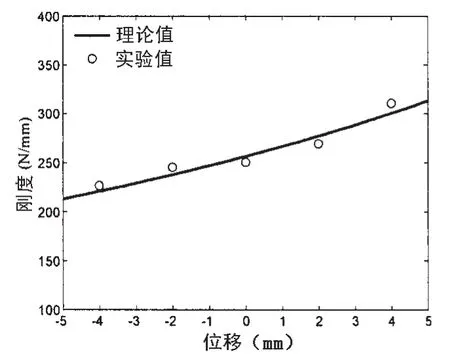
图2 气囊隔振器刚度随位移变化Fig.2 Stiffness of air-spring vs.displace

图3 修正后气囊隔振器刚度随位移变化Fig.3 Modified stiffness of air-spring vs.displace

由图2可以看出，由气囊隔振器刚度理论计算得到的结果与实验值偏差较小，说明文中采用的气囊刚度模型具有较高的精度。考虑到气囊隔振器中安装有磁悬浮作动器，气囊隔振器的刚度模型需进行修正。某型磁悬浮作动器的体积为Va，混合隔振器囊体体积变为V1=V-Va。经过体积修正后，气囊隔振器刚度随位移变化如图3所示。

1.2 磁悬浮作动器负刚度模型

磁悬浮作动器可以采用多种结构形式：上下电磁铁结构、引入直流偏置电流或使用永磁体偏置等方式。本文采用单边永磁偏置的E型磁悬浮结构[2]。如图4所示，其主要由铁芯、衔铁、永磁体、导磁橡胶以及线圈组成。永磁体在作动器磁回路中形成偏置磁场，从而对衔铁产生偏置吸引力。当给线圈通入交变的控制电流，就可获得交变的输出力。导磁橡胶粘贴在永磁体上表面，能提升气隙中的磁导率，从而提高作动器的输出力。另外，导磁橡胶具有弹性，能在衔铁与其接触时增加整个系统刚度。

填充导磁橡胶后，气隙磁导率增加，其效果相当于缩短作动器的气隙。可认为填充导磁橡胶后气隙高度变为原来的k倍（k＜1）。忽略漏磁、磁阻并假设气隙磁场均匀，由磁路欧姆定律可得到作动器输出力：

图4 磁悬浮作动器结构图Fig.4 Diagram of maglev actuator

式中：g是衔铁、永磁体间的气隙高度，h为永磁体厚度，S1和S2分别是内外铁芯与衔铁的正对面积，μ0和μr分别是真空磁导率和永磁体的相对磁导率，Fm为永磁体产生的磁势，N和i分别为线圈匝数和电流。不进行主动控制时，由永磁体产生的静态偏置吸引力为：

其中：

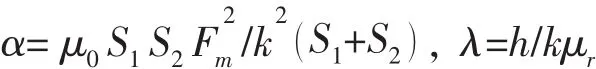
针对（6）式中忽略漏磁、磁阻以及所做的磁场均匀假设带来的误差，本文结合某型磁悬浮作动器实验数据，采用曲线拟合的方法对（6）式进行参数辨识，得到图5和表1的结果。

气囊在额定载荷下，作动器初始气隙为5 mm，作动器的气隙与气囊上盖板位移之间的关系为g= 5-z。由（6）式可得到作动器的偏置力与气囊盖板位移之间的关系式为：

表1 作动器辨识参数Tab.1 Identified parameters of the actuator

1.4 混合隔振器刚度模型

磁悬浮主被动混合隔振器可以看做是单自由度弹性系统。当作动器衔铁不与导磁橡胶接触时，混合隔振器刚度由气囊正刚度Ks和磁悬浮作动器等效负刚度Ka两部分并联；当作动器衔铁与导磁橡胶接触时，混合隔振器刚度由气囊正刚度Ks、磁悬浮作动器等效负刚度Ka以及导磁橡胶的刚度Kr三部分并联。按气囊盖板位移行程z进行划分，混合隔振器总刚度可表达为：

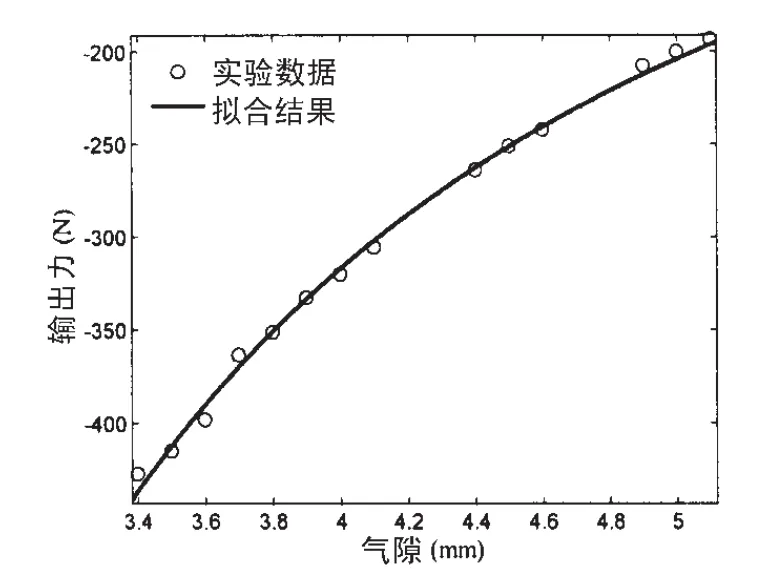
图5 作动器的偏置力随气隙变化Fig.5 Bias force of actuator vs.air-gap

图6 作动器等效负刚度随位移变化Fig.6 Negative stiffness of actuator vs.displace

由（7）式可以看出，随着位移增加，作动器的偏置吸引力逐渐增大，作动器表现为对位移的负刚度。将上式对位移z求导，可得到作动器等效位移负刚度为：

2 混合隔振器静稳定性分析

2.1 单自由度弹性系统静稳定性判定准则

若一受载发生弹性形变并达到平衡状态的结构在微小扰动作用下稍微偏离其平衡位置后，能回到或有趋势回到原平衡位置，则称此平衡态是静稳定的。对处于平衡状态的弹性系统，根据虚功原理[10]：

其中：δWF为主动力对应的虚功，N为广义坐标数，Qk为与广义坐标qk对应的广义力：

式中：x，y，z为质点的自然坐标，Fx，Fy，Fz为自然坐标下对应的主动力。由于作用在弹性系统质点上的主动力都是有势力，各力的投影都可以写成用势能V的表达的形式：

于是有：

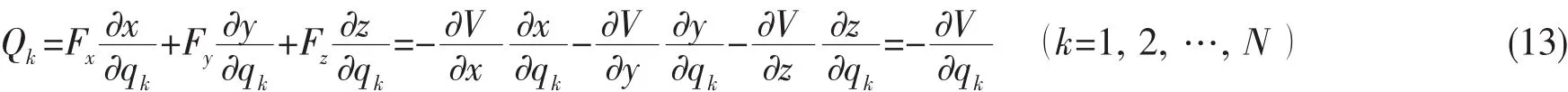
由于广义坐标的独特性，δqk可任意取值，所以必须满足：

由（14）式可知，在势力场中，弹性系统平衡的条件是势能对于每个广义坐标的偏导数分别等于零，即势能具有极值。满足平衡条件的弹性系统可能处于不同的平衡状态：稳定平衡、随遇平衡和不稳定平衡。在稳定平衡位置处，由于系统受到扰动后能回到原平衡位置，因此系统势能具有极小值，而不稳定平衡处，系统势能具有极大值[10]。对于单自由度弹性系统，q为系统位移。系统势能函数为：

系统刚度为有势力对位移的负导数，即：

由（16）式可以看出，单自由度弹性系统的刚度等于系统势能函数对位移的二阶导数。因此，单自由度弹性系统的静稳定性判定准则为：

2.2 稳定性分析

某型磁悬浮主被动混合隔振器在6.1 kN的额定载荷下保持平衡，此时磁悬浮作动器的初始气隙为5 mm。由于磁悬浮作动器气隙中填充了3 mm导磁橡胶，混合隔振器正常工作时衔铁不与导磁橡胶接触，因此主被动混合隔振器的工作气隙大于3 mm，对应的工作位移小于2 mm。

当混合隔振器盖板位移区间为负时，由图3和图6可以看出，此区间内作动器等效负刚度绝对值均比气囊正刚度小，系统刚度始终为正，根据稳定性判定准则可判定该区间内混合隔振器是静稳定的。

当混合隔振器盖板位移区间为0-2 mm时，根据前面系统刚度模型，可计算出主被动混合隔振器系统总刚度随位移变化关系如图7所示。

由图7可以看出，在2 mm的工作位移内，由于磁悬浮作动器的等效负刚度的影响，混合隔振器总刚度随着位移增大而减小，但总刚度始终为正。根据稳定性判定准则可知，混合隔振器在工作位移内是静态稳定的。

当盖板超出2 mm的工作位移时，衔铁开始与导磁橡胶接触，混合隔振器刚度由气囊、作动器和橡胶三部分组成。实验测得导磁橡胶的等效位移刚度在3 000 N/mm以上，由于导磁橡胶刚度量级远超过气囊隔振器和磁悬浮作动器的刚度，因此该混合隔振器的总刚度会发生阶跃性增大，其系统刚度始终为正。根据稳定性判定准则，即使混合隔振器超出工作位移，其也是静稳定的。

由以上分析可知，该磁悬浮混合隔振器在小于2 mm的工作气隙内是静稳定的。即使混合隔振器盖板超出工作位移，系统总刚度同样为正，系统还是静稳定的。

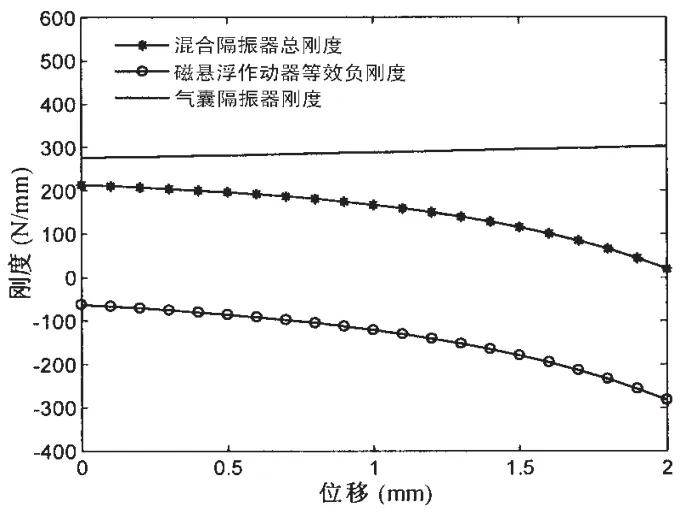
图7 主被动混合隔振器刚度随位移变化Fig.7 Stiffness of hybrid isolator vs.displace

3 实验验证

为了验证稳定性分析的准确性，本文将主被动混合隔振器，如图8所示，放在MTS landmark 370.50试验系统上进行静态加载实验，与之进行对比实验的还有同种型号但未安装作动器的气囊隔振器。试验前将混合隔振器以额定高度固定在试验机上，缓慢给混合隔振器充气，直到其垂向载荷达到6.1 kN时停止充气。试验采用位移方式控制，加载速率为0.1 mm/s，以此来模拟静态加载。取一个周期循环的静态载荷位移数据，得到如图9所示曲线。

图8 磁悬浮气囊主被动混合隔振器Fig.8 Passive-active vibration isolator combining maglev actuator and air spring

由图9可以看出，在小于2 mm的工作位移内，混合隔振器的载荷随气囊盖板位移增加而增大，相对气囊隔振器而言，其载荷位移曲线逐渐趋于水平，其斜率即混合隔振器刚度随位移逐渐减小，但总刚度始终大于零，根据稳定性判定准则，混合隔振器在工作位移内是静稳定的，这与前面的理论分析一致。当位移超过2 mm时，混合隔振器的载荷位移曲线发生突变，说明作动器衔铁开始与导磁橡胶接触。接触后载荷位移曲线斜率即隔振器总刚度变得很大，根据稳定性判定准则，在此位移区间内该混合隔振器也是静稳定的。

综合以上实验结果可知，该混合隔振器在工作位移内总刚度为正，隔振器是静稳定的。当超出工作位移时，由于导磁橡胶的作用，混合隔振器也是静稳定的。实验结果验证了理论分析的正确性。

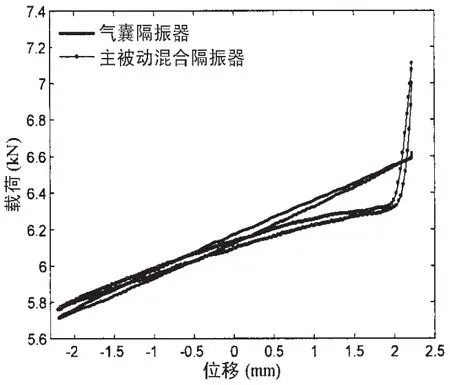
图9 气囊隔振器刚度随位移变化Fig.9 Stiffness of air-spring vs.displace

4 结 论

采用磁悬浮主被动混合隔振器进行设备隔振时，需对其进行静稳定性分析。本文从建立磁悬浮混合隔振器刚度模型出发，推导了判定单自由度弹性系统静稳定性的刚度准则，从理论上分析了某型磁悬浮主被动混合隔振器的静稳定性。随后对该混合隔振器进行MTS静态加载实验，通过实验验证了理论分析正确性。理论和实验结果表明，混合隔振器在工作位移内是静稳定的，即使超出工作位移，由于有导磁橡胶的保护，混合隔振器也不会失稳。但在实际使用时，为了使主动控制正常工作以及保护易脆的永磁体不受到过大的载荷，需对混合隔振器进行限位设计，确保盖板位移不超出2 mm。

致谢：本文工作得到了国防科技重点实验室基金（编号：SYSZC2012002）的资助。

[1]何 琳,徐 伟.舰船隔振装置技术及其进展[J].声学学报,2013,38(2):128-136. He Lin,Xu Wei.Naval vessel machinery mounting technology and its recent advances[J].Acta Acustica,2013,38(2):128-136.

[2]何 琳,李 彦,杨 军.磁悬浮—气囊主被动混合隔振装置理论和实验[J].声学学报,2013,38(2):241-249. He Lin,Li Yan,Yang Jun.Theory and experiment of passive-active hybrid vibration isolation mounts using electromagnetic actuator and air spring[J].Acta Acustica,2013,38(2):241-249.

[3]路纯红,白鸿柏,杨建春.超低频非线性隔振系统研究[J].噪声与振动控制,2010(4):10-12. Lu Chunhong,Bai Hongbai,Yang Jianchun.Research on ultra-low-frequency nonlinear vibration isolation system[J].Noise and Vibration Control,2010(4):10-12.

[4]Carrella A,Brennan M J,Waters T P.On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[J].Journal of Sound and Vibration,2008(315):712-720.

[5]Takeshi M,Masaya T,Daisuke K.Vibration isolation system combining zero-power magnetic suspension with springs[J]. Control Engineering Practice,2007(15):187-196.

[6]Daolin Xu,Qiping Yu,Jiaxi Zhou.Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic[J].Journal of Sound and Vibration,2013(332):3377-3389.

[7]何 琳,徐 伟,卜文俊,等.舰船推进动力系统新型隔振装置研制与应用[J].船舶力学,2013,17(11):1328-1338. He Lin,Xu Wei,Bu Wenjun,et al.Development and application of new-type mounting system for naval vessel propulsion system[J].Journal of Ship Mechanics,2013,17(11):1328-1338.

[8]彭解华,陈树年.正、负刚度并联结构的稳定性及应用研究[J].振动、测试与诊断,1995,15(2):14-18. Peng Jiehua,Chen Shunian.The stability and application of a structure with positive stiffness element and negative stiffness element[J].Journal of Vibration,Measurement&Diagnosis,1995,15(2):14-18.

[9]徐 伟.气囊减振装置技术研究[D].武汉:海军工程大学,2005. Xu wei.A study on the technology of pneumatic vibration isolation system[D].Wuhan:Naval University of Engineering, 2005.

[10]王振发.分析力学[M].北京:科学出版社,2007. Wang Zhenfa.Analytic mechanics[M].Beijing:Science Press,2007.

Static stability analysis of a passive-active hybrid vibration isolator

NI Yuan1,2,HE Lin1,2,SHUAI Chang-geng1,2,Li Yan1,2
(1 Institute of Noise&Vibration,Naval University of Engineering,Wuhan 430033,China；2 National Key Laboratory on Ship Vibration&Noise,Wuhan 430033,China)

Passive-active vibration isolator using maglev actuator is a elastic structure combining positive and negative stiffness.Stiffness model of the hybrid vibration isolator is established to solve the stability problem of the structure.According to virtual work principle,the stiffness principle determining the static stability of a elastic system is derived.This stiffness principle combining the stiffness model is used to analyze the static stability of the hybrid vibration isolator.Theory and experimental results show that the stiffness of the hybrid vibration isolator is positive for working displace,and the isolator is stable.

maglev actuator;air-spring;hybrid vibration isolator;static stability

TB535

A

10.3969/j.issn.1007-7294.2015.10.013

1007-7294（2015）10-1275-07

2015-05-28

国防科技重点实验室基金资助（SYSZC2012002）

倪 圆（1986-），男，博士研究生，E-mail:niyuan-1986@163.com；何 琳（1957-），男，教授。