服役后期海洋平台剩余寿命可靠度预测方法

刘 勇，陈炉云，侯国华

（1中国船舶科学研究中心 上海分部，上海 200011；2上海交通大学 船舶海洋与建筑工程学院，上海 200240；3总装备部 陆军装备科订购部，北京 100034）

服役后期海洋平台剩余寿命可靠度预测方法

刘 勇1，陈炉云2，侯国华3

（1中国船舶科学研究中心 上海分部，上海 200011；2上海交通大学 船舶海洋与建筑工程学院，上海 200240；3总装备部 陆军装备科订购部，北京 100034）

为保证服役后期平台在延寿服役期内的安全性，需要对其结构整体剩余寿命可靠度进行预测。因此，文章重点研究了在随机波浪载荷作用下平台部分构件动力失效和疲劳失效时，平台整体时变可靠度预测方法。采用Miner线性累积损伤理论和首次超越失效准则，计算平台构件的疲劳寿命可靠度和动力可靠度，搜索并删除失效概率较大的构件，运用波浪增量动力分析法找出平台结构所能承受的极限波浪载荷，再结合服役海域波浪统计资料，计算平台结构系统整体时变可靠度以预测其剩余寿命。文中算例表明了该方法的实用性和简便性。

海洋平台；剩余寿命可靠度；随机波浪；波浪增量动力分析

0 引 言

随着海上油气开发的不断发展，一些接近或达到设计寿命的海洋平台将继续服役，以满足油田开发的需要。因此迫切需要对现役平台进行安全评估，以确保平台的安全服役，最大限度地延长其使用寿命并对其剩余寿命可靠度进行预测。

Onoufriou等[1]总结了近些年固定式海洋平台可靠性评估的进展。Golafshani等[2]提出了波浪增量动力可靠性分析方法用以计算在海洋平台整体倒塌概率。在国内，欧进萍等[3]提出了导管架式海洋平台结构极限承载力分析的整体推进法。王文明等[4]分别计算了四种不同工况下平台在单个构件失效后的极限承载力以及单个构件失效后平台结构的剩余强度系数，以分析单个构件失效对导管架平台极限承载力的影响。刘海丰[5]对老龄平台结构在复杂海洋环境下的剩余强度分析和安全可靠性评估方法进行了研究。

海洋平台是由成千上百个构件组成的高次超静定结构，其失效过程一般是少数构件失效，但不一定会导致平台整体结构失效，当失效构件逐渐累计到一定程度时，平台才会发生垮塌。本文从服役环境中平台整体失效实际过程出发，从系统的角度对平台结构整体时变可靠度预测方法进行研究。

1 平台构件疲劳可靠性分析

海洋波浪的长期分布可以看成是由许多短期海况的序列组成的，在每一个短期海况中，假设构件的应力幅值服从Rayleigh分布：

根据Miner线性累积损伤理论和应力幅值与疲劳寿命关系曲线，构件的疲劳寿命为

式中：A为描述S-N曲线的随机变量；B为描述疲劳分析中应力范围计算过程中不确定因素的随机变量；Ω为应力参数；m为描述S-N曲线的确定量；Δ为描述结构疲劳破坏累积损伤度的随机变量。

2 平台构件动力可靠性分析

本文在计算平台构件动力可靠度时，采用首次超越失效机制。所谓首次超越失效机制，就是假设结构在结构动力响应值（如控制点的应力、位移和加速度等）首次超越临界值或安全界限时，结构就会发生破坏或失效[7]。在服役后期平台构件动力可靠度分析中，当构件应力峰值大于材料屈服极限时认为该构件失效。

在每一个短期海况中，假设构件的应力峰值y服从Rayleigh分布：

对于波浪载荷下构件的振动响应，构件的破坏界限取材料屈服极限，为单侧界限。这时，构件在（0,t）时间内动力可靠度采用下式计算：

3 波浪增量动力分析

在确定平台所能承受的极限波浪载荷时，主要运用了波浪增量动力分析法。波浪增量动力分析是在波浪作用下对平台结构进行弹塑性动力时程分析，以波浪载荷为输入量，在分析过程中不断改变波浪载荷参数的大小，使导管架经历从弹性、非弹性直至倒塌的全过程，通过分析结构性能参数与波浪载荷参数之间的关系曲线，从而找到结构所能承载的极限载荷。当曲线的斜率突然发生改变时，意味着在波浪载荷有微小增加的情况下，结构性能参数发生显著变化，可以认为结构失去稳定性即将发生倒塌，此点的波浪载荷即为结构所能承载的极限载荷[2]。以波浪载荷参数和结构性能参数为坐标轴，可以绘制一条波浪增量动力分析曲线（见图1），通过此曲线就可以找到结构能够承受的极限波浪载荷。

图1 波浪增量动力分析曲线Fig.1 Wave incremental dynamic analysis curve

4 服役后期平台剩余寿命预测方法

4.1 基本思想

海洋平台结构复杂、构件众多，在进行整体剩余寿命可靠度预测时作以下假设：

（1）在1年中的失效构件可靠性模型为串联系统，因为串联系统的失效概率大于并联系统以及混联系统，这样处理使得最后的计算结果偏于安全，符合工程需要。将1a中的失效构件作为一个等效失效单元，其失效概率为

式中：PEn为在第na等效单元的失效概率；Pjn表示在第n年失效构件的失效概率；j=1,2,…m为具有较大失效概率构件的个数。

（2）以年为时间单位，在1年中构件的失效概率和平台的整体失效概率是不变的，以年末的计算值表示这一年的构件和平台整体失效概率。

（3）在计算平台整体结构的失效概率时，不考虑平台结构的随机性。

首先根据上述构件疲劳可靠性和动力可靠性分析方法，逐年预测构件的疲劳和动力失效概率，删除失效概率大于规定阈值的构件，同时把这些构件作为一个等效失效单元，计算其失效概率。然后运用波浪增量动力分析法求得平台在第n年所能承受的极限波高Hmax，平台结构整体失效概率即为极限波高年超越概率。

式中：PSn为在第n年有构件失效的情况下平台结构整体失效条件概率为平台所能承载的极限波高的年超越概率。

根据（6）式和（7）式，第n年服役期间平台结构整体失效概率为

平台又连续服役了nl年，其整体时变可靠度为

式中：nl=n-n0，n0为平台已经服役的时间，接近其设计寿命。

4.2 步骤

服役后期平台剩余寿命预测方法步骤如下：

（1）按照前面介绍的构件疲劳可靠性分析方法，计算构件经过n0a服役后疲劳积累损伤Dn0和疲劳寿命的可靠度，如果某个构件疲劳寿命可靠度小于规定的阈值，则判定其失效，删除该构件。

（2）按照前面介绍的构件疲劳可靠性分析方法，按照下式计算各构件在na服役期间内的疲劳寿命：

式中：Dn为在第na服役期间内波浪载荷造成的疲劳损伤。如果某个管节点疲劳寿命概率可靠性小于规定的阈值，则判定其失效，删除该构件。

（3）按照前面介绍的构件动力可靠性分析方法，计算平台各个构件在第na服役期间内的动力可靠度。如果某个构件的动力可靠度小于材料屈服极限，则判定其失效，删除该构件。

（4）采用波浪增量动力分析法计算平台在第na服役期间所能承载的极限浪高Hmax。

（5）按照（8）式计算在第n年服役期间平台整体失效概率，按照（9）式计算平台连续服役了nl年整体可靠度。

（6）重复步骤(2)～(5)，直至平台剩余寿命可靠度R（nl）低于规定的阈值，停止计算，所得到时间nl即为平台的剩余寿命。

5 算 例

以埕岛油田某服役后期井组平台的计量平台为例，对其整体剩余寿命进行预测。该平台导管架采用四腿型式，导管架顶标高5.0 m，底标高-10.5 m，工作点标高5.5 m。主导管采用Φ1 340 mm×25 mm钢管，成矩形布置；在标高-2 m、4.0 m之间设竖向斜拉筋，采用Φ610 mm×20 mm钢管。桩采用Φ1 200 mm×25 mm开口变壁厚钢管桩，桩入泥深度25 m。

（1）根据计量平台的现场勘测资科，建立有限元模型（图2）。充分考虑平台结构腐蚀、桩基冲刷、海生物附着等情况影响，并且通过地基反力法模拟桩—土交互作用，对真实的结构进行简化处理，结构的简化保证主体结构几何形状的真实性，结构振动频率和振型的真实性[8]。

（2）根据Morrison公式将海浪谱转化为波浪力谱，运用谱分析方法，计算各构件的疲劳寿命可靠度和动力可靠度。在计算构件疲劳可靠度时，管节点应力集中系数为2。由于平台结构对称，忽略海浪的方向性。构件失效概率阈值取0.003。构件疲劳寿命可靠度和动力可靠度计算结果如表1、2所示。表1中×表示失效概率大于阈值，构件已失效，将不再计算它们的失效概率；表2中只选取部分构件的动力可靠度计算结果。

图2 平台有限元模型Fig.2 Platform finite element model

（3）计算每年等效单元失效概率，计算结果对应n=1，2，3a的Pn=0.011 5，0.013 5，0.240 6。

（4）运用波浪增量动力分析法计算平台所能承受的极限波高。选取导管架顶端转角最大值θmax为结构性能参数，波高为波浪载荷参数。各种海况下的分析时间选取为1h。参照FEMA-35l[9]规范，取曲线斜率小于初始斜率的20%的点为结构不倒塌极限状态点。根据埕岛油田海域年波高统计资料，年最大波高概率分布函数取三参数威布尔函数，2.359 59，C=2.310 09。平台每年所能承载的极限波高及极限波高超越概率如表4所示。

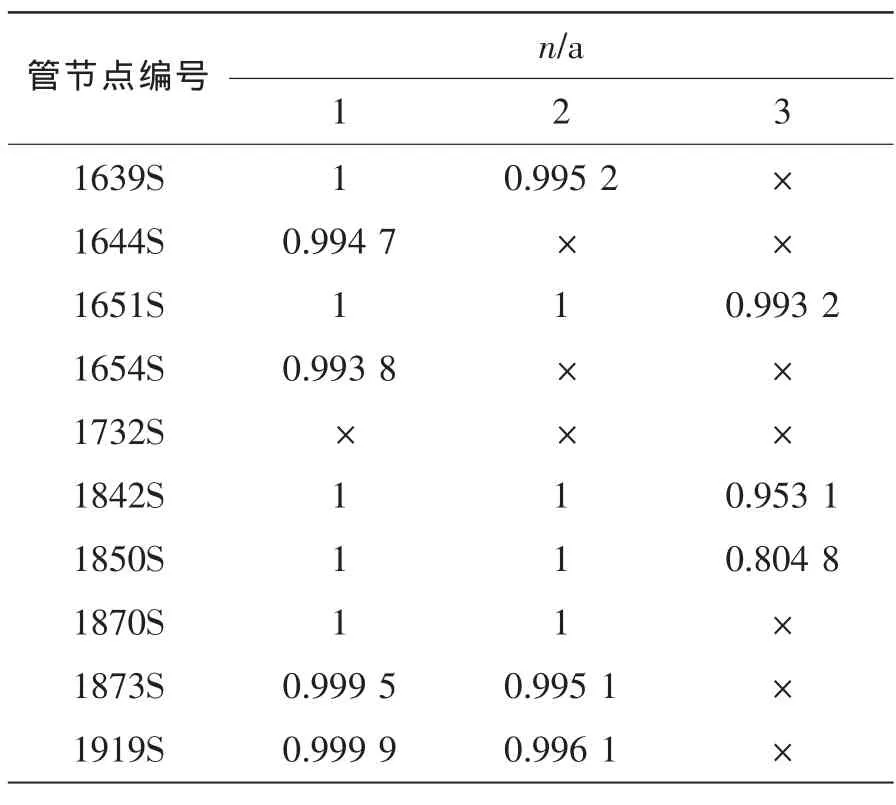
表1 管节点疲劳寿命可靠度Tab.1 Tubular joints fatigue life reliability

表2 构件动力可靠度Tab.2 Components dynamic reliability

表3 极限波高和极限波高超越概率Tab.3 Limiting wave height and probability of exceedance

（5）逐年计算平台结构整体可靠度，预测剩余寿命。对应于n=1，2，3a的平台整体可靠度为1.0，1.0，0.991 8。假设平台整体可靠度的阈值为0.997，则服役后期平台在第3年整体可靠度小于阈值，其剩余寿命为2年。

5 结 语

本文重点研究了在随机波浪载荷的作用下当部分平台构件动力失效和疲劳失效时，平台整体时变可靠度预测方法。该方法较好地模拟了海洋平台在服役环境中的实际失效过程，最后的算例证明该方法具有工程应用价值。

[1]Onoufriou T,Forbes V J．Developments in structural system reliability assessments of fixed steel offshore platforms[J]．Reliability Engineering and System Safety,2001,71:189-199．

[2]Golafshani Ali Akbar,Ebrahimian Hossein,Bagheri Vahid,Holmas Tore．Assessment of offshore platforms under extreme waves by probabilistic incremental wave analysis[J]．Journal of Constructional Steel Research,2011,67:759-769．

[3]欧进萍,肖仪清,刘学东,等．导管架式海洋平台结构极限承载力分析的整体推进法及其软件[J].海洋工程,1999,17 (3):1-10．Ou Jinping,Xiao Yiqing,Liu Xuedong,et al.Whole stepwise push method of ultimate strength analysis of jacket offshore platform structures and its computer program[J].Ocean Engineering,1999,17(3):1-10．

[4]王文明,张世联．导管架平台极限承载力的有限元解法[J]．中国海洋平台,2006,21(5):27-33．Wang Wenming,Zhang Shilian.Analyses of ultimate strength of jacket platforms by finite element method[J].China offshore platform,2006,21(5):27-33．

[5]刘海丰．面向老龄平台延寿工程的结构风险评估技术研究[D].北京:中国石油大学,2009．Liu Haifeng.Structural risk assessment of aged offshore platform for life extension engineering[D].Beijing:China University of Petroleum,2009．

[6]彭 攀．导管架海洋平台疲劳可靠性分析[D]．南京:河海大学,2008．Peng Pan.Fatigue reliability analysis of a Jacket Platform[D].Nanjing:Hohai University,2008.

[7]李桂青,李秋胜．响应谱MC模拟的桥梁抖振首次超越研究[J]．工程力学,2006,23(1):123-129．Li Guiqing,Li Qiusheng.Monte Carlo simulation approach to first passage probability in bridge buffeting response[J].Engineering Mechanics,2006,23(1):123-129．

[8]张大勇,岳前进,刘 笛,等．自升式钻井平台的抗冰性能评价[J]．船舶力学,2015,19(7):850-858．Zhang Dayong,Yue Qianjin,Liu Di,at el.Structural ice-resistant performance evaluation of jack-up drilling platforms[J]. Journal of ship Mechanics,2015,19(7):850-858．

[9]Report No.FEMA-35l．Recommended seismic evaluation and upgrade criteria for existing welded steel moment-frame Buildings[S]．

Study on post-service Jacket platform residual life reliability prediction method

LIU Yong1,CHEN Lu-yun2,HOU Guo-hua3
(1 Shanghai Branch,China Ship Scientific Research Center,Shanghai 200011,China; 2 School of Naval Architecture,Ocean and Civil Eng.,Shanghai Jiao Tong Univ.,Shanghai 200240,China;3 Army Equipment Science Research Purchase Department,PLA General Equipment Department,Beijing 100034,China)

To ensure the post-service platform security in the late service period,it is necessary to predict platform structure residual life reliability.In this paper,platform global time-varying reliability resulting from component dynamic failure and fatigue failure under random wave loads are studied.Component fatigue reliability and dynamic reliability are calculated according to Miner linear cumulative damage theory and first crossing failure criteria,components with larger failure probability are searched and deleted.The wave incremental dynamic analysis is used to find the limiting wave height that the platform could bear.Finally, combining with the wave statistics,platform global structure time-varying reliability is calculated to predict the residual life.The example shows the practicality and simplicity of the proposed method.

offshore platform;residual life reliability;random wave;wave incremental dynamic analysis

U661.4

A

10.3969/j.issn.1007-7294.2015.10.010

1007-7294（2015）10-1255-06

2015-07-25

刘 勇（1980-），男，博士，工程师，E-mail:flydark@126.com；

陈炉云（1975-），男，博士，助理研究员，E-mail:cluyun@163.com。