基于FGU的船体变形测量技术中时间延迟补偿方法研究

徐 博，陈 春，史宏洋，郭 宇

（哈尔滨工程大学 自动化学院，哈尔滨 150001）

基于FGU的船体变形测量技术中时间延迟补偿方法研究

徐 博，陈 春，史宏洋，郭 宇

（哈尔滨工程大学 自动化学院，哈尔滨 150001）

基于光纤惯性测量单元（Fiber Gyro Unit，简称FGU）的角速率匹配法是船体变形测量技术的发展方向，但是在实际应用中两套测量单元之间存在时间延迟，会影响船体变形测量精度。该文分析了时间延迟的产生机理以及时间延迟对变形估计的影响。并基于二阶马尔科夫模型对船体变形建模，建立卡尔曼滤波状态方程和量测方程，提出了一种时间延迟补偿方法，将时间延迟扩充为状态量，对其进行实时的估计和补偿。最后通过仿真并结合实船试验数据，对比分析了时间延迟补偿前后的变形估计效果，验证了此方法的有效性。

船体变形；角速率匹配法；时间延迟；实船测量；补偿方法

measurement of the real ship;compensation method;Fiber Gyro Unit

0 引 言

舰船在海上航行时，受到许多因素的影响，舰船甲板会产生不可忽视的变形。使得由主惯导（MINS）向舰载武器系统和侦查探测系统等各战位点发送的姿态仅为MINS处的姿态，并非各战位点的载体坐标系相对于导航坐标系的当地坐标系，MINS与局部位置间的姿态差异将严重影响舰载武器系统的精度。

与以结构力学为理论基础的测量方法，如光栅法、双频偏振光法相比[1]，基于惯性测量单元的船体变形测量方法具有成本低、动态适应性好、安装方便等优点，是今后船体变形测量的发展趋势。基于角速率匹配法构建的船体变形测量系统属于分布式测量系统，时间延迟是分布式测量系统普遍面临和必须解决的问题。关于角速率匹配法测量船体变形的理论研究已有诸多成果[2-7]，但对该方法的实际应用则很少谈及。文献[8]提出利用激光陀螺作为惯性测量单元，结合角速率匹配法和卡尔曼滤波技术对船体变形进行测量，但并未进行实船试验，更没有谈及时间延迟对角速率匹配法的影响及补偿方法。

传递对准是指用高精度的主惯导的速度和姿态信息对准子惯导信息，角速率匹配是指利用两套惯导的角速率信息估计出相对变形角，两种方法的测量原理有相似之处。关于传递对准中的时间延迟问题的补偿方法，文献[9]提出一种外推滤波法，可以很好地解决传递对准中的时间延迟问题，但必须预先知道时间延迟大小才能进行外推，而角速率匹配法所面临的时间延迟无法预先测量。文献[10]则提出一种状态补偿法，对传递对准中的时间延迟进行了补偿，该方法也必须预先知道时间延迟的大小，进而进行状态补偿。

本文基于实船试验中发现的两套惯性测量单元之间存在时间延迟，会对船体变形角的测量产生影响的问题，分析了时间延迟对船体变形测量的影响，并结合俄罗斯学者Mochalov提出的船体变形角模型，给出了一种时间延迟补偿方法，并结合实船数据验证了该补偿方法的测量效果，为船体变形测量技术的实际应用提供技术支撑。

1 角速率匹配法测量船体变形的原理

1.1 船体变形的成因

舰船在海上航行时，受到海浪冲击、载物再分布、武器发射时产生的冲击、转舵操作和环境温度变化等因素的影响，船体会发生变形。船体变形可分为静态变形和动态变形两种。舰船在日晒夜露和时间老化作用下结构和形状逐渐变化，就会产生长期变形，此种变形为静态变形，静态形变可高达1°～1.5°。船体的动态变形主要发生在恶劣海情下波浪运动对船体加载的影响，任意两点间角位移的幅值随着其间距离的加大而增大，当船体机动减摇装置作用或船艏升离水面重又入水时，可能产生瞬时的船体挠曲变形，其他突发性的变化可由水下冲击产生[11]。

1.2 角速率匹配法测量原理

将两个光纤陀螺测量单元（Fiber Gyro Unit，简称FGU）分别安装在船体的中间和船头二个位置（分别为FGU1和FGU2），如图1所示。FGU1与FGU2的三轴所指方向如图1示，y轴沿着船体纵向指向船艏，z轴垂直于甲板平面指天，x轴与上述两轴构成右手正交坐标系，由此可得与FGU1固联的坐标系oxyz和与FGU2固联的坐标系o′x′y′z′。

图1 光纤陀螺安装示意图Fig.1 The diagrammatic sketch of install fiber optic gyro

图2 变形角示意图Fig.2 The diagrammatic sketch of angle of deformation

FGU1测量的是地球自转和船体运动在FGU1载体坐标系中的投影；而FGU2测量的是上述两项在FGU2载体坐标系中的投影，以及FGU2安装点相对于舰船中心的变形所引起的角速率之和。由于船体变形的存在，使得FGU1与FGU2的输出存在差别，该差别可以反映两个安装点间的相对静态和动态变形。

如图2所示，设两组FGU安装点间的形变角由静态形变Φ和动态形变θ两个部分组成，则总的变形量为：φ=Φ+θ，其中静态变形为常值变形，而动态变形为随机变形。则有Φ˙=0，φ˙=θ˙，总的变形量表示成矩阵形式为：

则FGU1测得的Ω与FGU2测得的Ω′存在如下关系：

当oxyz坐标系和o′x′y′z′坐标系存在变形角时，两坐标系有如下关系：

其中B是方向余弦阵[3]。

则由（1）式可得到：

设FGU1与FGU2输出的角速率差为ΔΩ，则有如下等式成立：

将（4）式表示成矩阵形式，则有

则（4）式可变换成：

根据上述推导及文献[8]所述的构建卡尔曼滤波器模型的方法，以两套光纤陀螺输出的角速率作为观测量选取合适的状态变量构建量测方程和状态方程，便可以估计出两个安装点之间的相对变形。

2 实船测量中时间延迟的影响因素分析

2.1 角速率匹配法的实船验证实验

通过实际测量我们发现，虽然利用GPS时刻作为计算机同步接收两套陀螺输出信息的起始时刻，但是由于时间延迟的存在，导致此后在接收角速率数据时出现不同步的现象。导致时间延迟的因素有很多，主要有以下几个方面：（1）信息采集的时间延迟。由于信息输出与信息采集是两个过程，则t时刻的信息被采集到的时候有可能是t+Δt时刻的数据信息，也可能是t+2Δt时刻的数据值，这样就会产生延时误差。一般而言，从一个测量单元的信息传递到另一个的时间延迟在40 ms到120 ms，信息延迟对测量精度的影响很大。时延过大，造成测量偏差较大，收敛时间增加，精度降低。（2）信息传输的时间延时。由于算法在子惯导中进行，需要将主惯导系统的一些相关信息传输到子惯导系统。如果是无线电导航或者传输迅速的手段对传输延时影响较小，而如果主子惯导距离较远且传输线路的材质密度不同，则会不同程度影响到传输速度而产生延时误差。但是在一次测量实验过程中，该延迟相对固定。

2.2 时间延迟对角速率匹配法的影响

在使用仿真验证角速率匹配算法的时候，我们认为两套FGU的输出完全同步。但在实船测量时，由于多种原因导致的时间延迟而不能绝对的同步输出角速率信息，从而会导致角速率匹配法在实际应用中会引入估计误差。图3-10分别针对没有延迟，以及不同大小的时间延迟对滤波估计精度的影响（一个延迟周期为10 ms）。

从图3～10中可以得出如下结论：

（1）时间延迟会导致卡尔曼滤波器的收敛速度变慢，使得角速率匹配法对静态变形角和动态变形角的估计需要经过多次振荡才能收敛。

图3 无延迟静态变形角估计曲线Fig.3 The evaluation of curve for no delay static state angle of deformation

图4 无延迟动态变形角估计曲线Fig.4 The evaluation of curve for no delay dynamic state angle of deformation

图5 延迟1个周期静态变形角估计曲线Fig.5 The evaluation of curve for delay 1 cycle static state angle of deformation

图6 延迟1个周期动态变形角估计曲线Fig.6 The evaluation of curve for delay 1 cycle dynamic state angle of deformation

（2）时间延迟会导致角速率匹配法对船体变形角的估计误差变大，对动态变形角的估计误差尤为显著。

（3）时间延迟越大对滤波精度的影响也越大，过大时间延迟会导致滤波发散，使得角速率匹配法对船体变形角的估计失效。

图7 延迟2个周期静态变形角估计曲线Fig.7 The evaluation of curve for delay 2 cycle static state angle of deformation

图8 延迟2个周期动态变形角估计曲线Fig.8 The evaluation of curve for delay 2 cycle dynamic state angle of deformation

图9 延迟4个周期静态变形角估计曲线Fig.9 The evaluation of curve for delay 4 cycle static state angle of deformation

图10 延迟4个周期动态变形角估计曲线Fig.10 The evaluation of curve for delay 4 cycle dynamic state angle of deformation

3 时间延迟补偿方法研究

3.1 引入时间延迟的卡尔曼滤波器的建立

实船测量时，两套光纤陀螺实际输出的角速率如图11所示，由于时间延迟的存在使得两套陀螺不能同步输出角速率信息，而且时间延迟存在长期的累积误差，图11中箭头表示FGU1的输出时刻对应于FGU2的输出时刻。

图11 两套陀螺按时间序列输出角速率Fig.11 The output angular rate for double gyroscopes

在应用角速率匹配法时，如图12所示，理论上默认为两套陀螺在t时刻同时输出角速率信息，并以ΔΩ=Ωt-Ωt′作为观测量进行卡尔曼滤波估计。但是在实际应用中，由于时间延迟的存在，使得其中一套陀螺在t1时刻输出角速率数据时，另一套陀螺则在t2时刻输出角速率数据，因此是以ΔΩ=Ωt2-Ωt1′为观测量进行卡尔曼滤波估计的。

如图12所示，无延迟时，在t2时刻两套陀螺存在某一变形角，根据（4）式可得：

如图13所示，对于o′x′y′z′坐标系来讲，o′x′y′z′在t1与t2时刻必然存在一定的角速度差，同时根据微分方程的知识，则有：

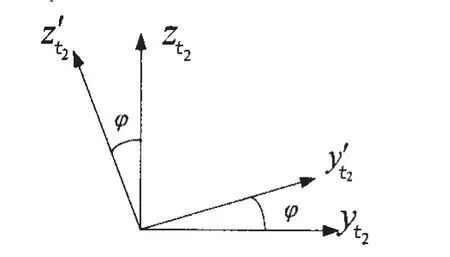
图12 oxyz与o′x′y′z′之间的变形角示意图Fig.12 The diagrammatic sketch of angle of deformation for oxyz and o′x′y′z′

图13 oxyz在t1与t2时刻之间的变形角示意图Fig.13 The diagrammatic sketch of angle of deformation for oxyz between t1to t2

由（6）式与（7）式相加可得：

式中B为：

则（8）式写成矩阵形式为：

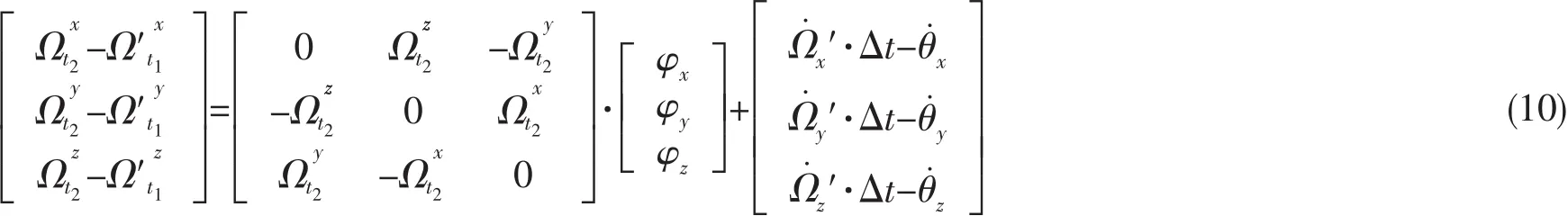
将（10）式表示为

其中：

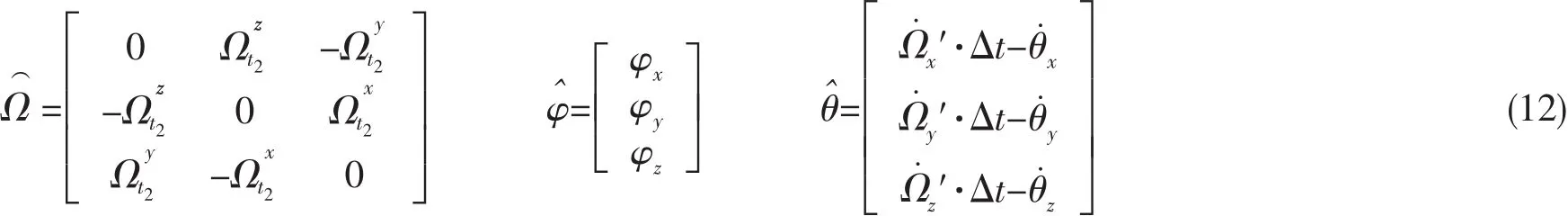
实际测量时，两套FGU以采样频率f输出角速率信息（理想情况下，两套陀螺同频同步输出角速率信息），由于两套陀螺之间存在时间延迟。不失一般性，当延迟Δt发生在］区间内，其中k，i为正整数，则（11）式中。由于两套系统的采样频率均较高（100 Hz），可以用该区间内的角速率均值代替该区间内任意时刻的角速率。实际测量时延迟Δt不可预先获得，但是可以将Δt作为一个常值状态变量扩充到卡尔曼滤波方程中。

根据文献[1]所述的构建量测方程的方法，并结合（11）式可以得到：

同样按照文献[8]中介绍的方法，选取静态变形角Φ、动态变形角θ、动态变形角的一阶微分θ˙、两套光纤陀螺的常值漂移′和随机漂移D、D′作为状态变量，此时需要将时间延迟扩充为状态变量：

由（13）式构建考虑到时间延迟的量测方程：

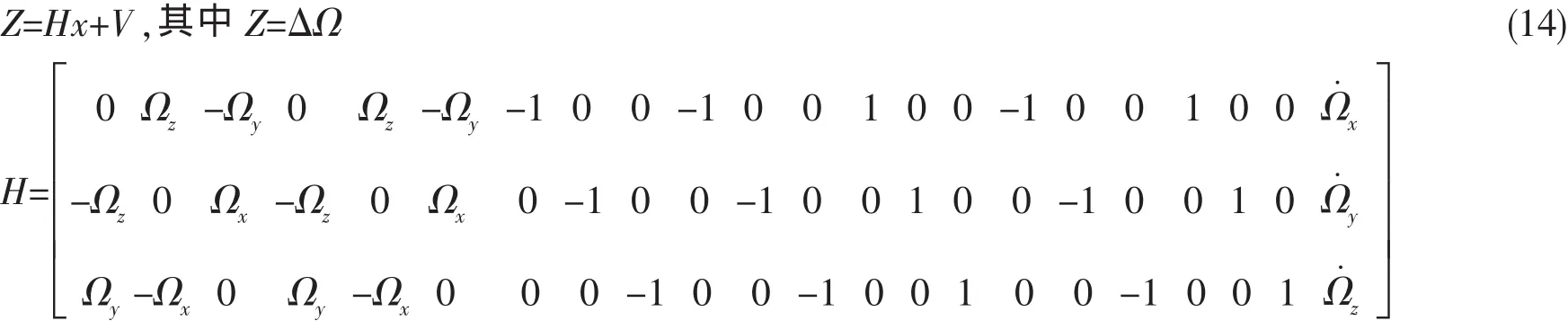
对于状态方程的建立，因为陀螺漂移的模型以及动态变形角模型并没有发生变化，而且我们将时间延迟默认为一个常值，则其有如下式子：

因此引用文献[8]中所述的状态方程，并将（15）式扩充进去则有：

其中：系数矩阵A和B中的非零元素同文献[8]所述的基础上维数进行了相应的增加。矩阵W是白噪声矩阵，维数也进行了相应增加。

3.2 时间延迟下的理论仿真分析

下面应用上述时间延迟补偿方法，分别对不同的时间延迟进行了补偿效果仿真，如图14～21所示。同时为了研究本文所述的时间延迟补偿方法的适用范围，逐渐加大时间延迟，并分别观察该方法对静态变形角和动态变形角的估计效果（一个延迟周期为10 ms）。

从图14～21可以得出以下结论：

（1）通过对时间延迟进行补偿，提高了角速率匹配法对船体变形角估计的收敛速度。

图14 延迟1个周期并补偿 Fig.14 The delay 1 cycle and compensation

图15 延迟1个周期并补偿Fig.15 The delay 1 cycle and compensation

图16 延迟2个周期并补偿 Fig.16 The delay 2 cycle and compensation

图17 延迟2个周期并补偿Fig.17 The delay 2 cycle and compensation

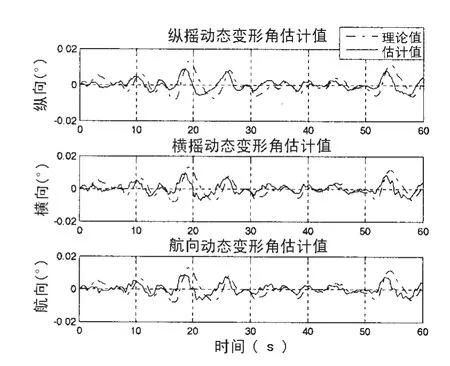
图19 延迟3个周期并补偿Fig.19 The delay 3 cycle and compensation

图18 延迟3个周期并补偿Fig.18 The delay 3 cycle and compensation

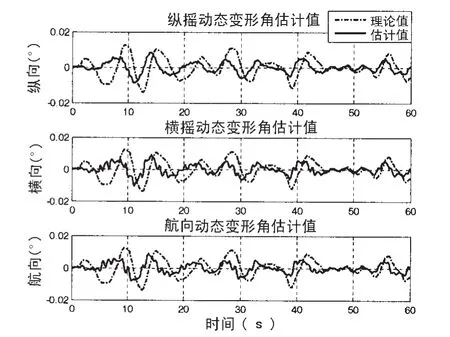
图21 延迟5个周期并补偿Fig.21 The delay 5 cycle and compensation

图20 延迟5个周期并补偿Fig.20 The delay 5 cycle and compensation

（2）通过将时间延迟扩充到卡尔曼滤波器中，可以准确估计出时间延迟的大小。

（3）通过对时间延迟进行补偿，角速率匹配法对静态变形角的估计对延迟大小的影响不敏感，即使时间延迟很大，估计效果也较好。

（4）通过对时间延迟进行补偿，当时间延迟较小时（发生在40ms以内），角速率匹配法对动态变形角的估计误差较小，但当延迟较大时，该方法对动态变形角的估计误差很大。

（5）该方法对延迟发生在一个采样周期内的估计效果最佳。

4 基于实船数据的时间延迟补偿方法效果验证

基于本教研室自主研发的光纤陀螺惯性测量单元，进行了实船试验。包括海上漂泊实验、码头锚泊实验和航行实验，其中海上航行实验过程经历了多次转舵操作，转舵操作会导致较大的船体变形发生。设备的安装如图22所示。

为了验证本算法的实用性，选取某段海上航行的实验数据进行分析。对实船数据进行离线处理时，我们根据GPS的时间戳将两套陀螺的输出数据进行人工对齐，得到一组无延迟的数据。然后通过MATLAB软件对该段数据进行时序处理，使得两套光纤陀螺惯性测量单元的输出在该段时间内存在10ms左右的延迟，进行离线处理。并对三组曲线进行比对分析：分别包括无延迟的估计曲线、有延迟不补偿的估计曲线以及有延迟进行补偿的估计曲线。图23和图24分别表示将三条静态变形角估计曲线和动态变形角估计曲线置于同一坐标系下，同时为了便于观察比较，将图中的曲线进行了放大处理，分别如图25和图26所示。

图22 光纤陀螺设备Fig.22 The Fiber optic gyro device

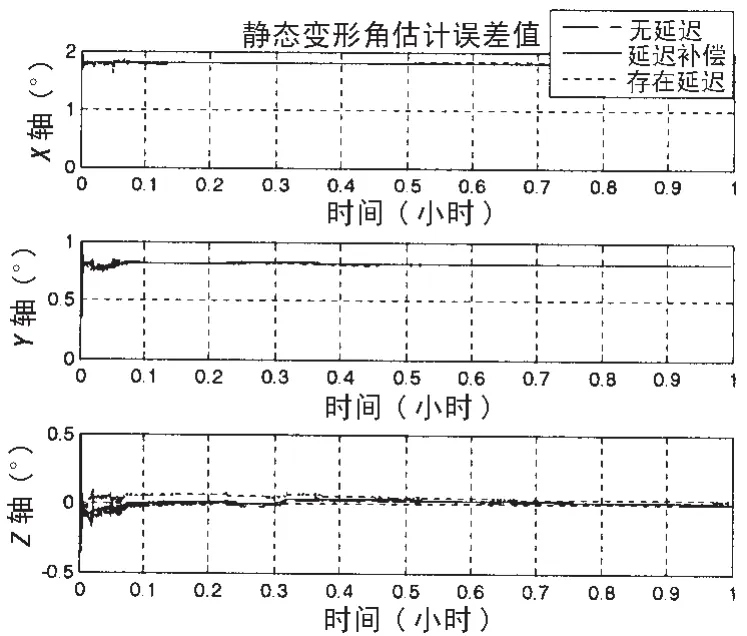
图23 三条静态变形角估计曲线Fig.23 The 3 static deformation curves of angle estimation

图24 补偿后的动态变形角估计Fig.24 The dynamic deformation angle estimation after compensation

图25 放大处理后的曲线Fig.25 Amplification curves after processing

图26 放大处理后的曲线Fig.26 Amplification curves after processing

由以上图中曲线，可以得到以下结论：

存在时间延迟的估计曲线与无延迟的估计曲线之间存在非常明显的误差，而经过时间延迟补偿的估计曲线与无延迟的估计曲线之间的误差非常小，从而可以看出，实船试验的分析结果和理论仿真结论基本吻合，由此验证了该算法的适用性。

5 结 论

在应用角速率匹配法进行实船测量船体变形时，不同的惯性测量单元之间存在时间延迟，该延迟会导致角速率匹配法测量的船体变形值存在较大误差，甚至会导致该方法失效。针对此问题，本文基于船体变形角模型，引入时间延迟因子，提出了一种时间延迟补偿方法，并通过了仿真验证，结合实船试验数据处理，验证了该方法的有效性。但是有些情况下，实际系统中的时间延迟是不确定的，且有可能存在长期累积误差，如何对随时间积累的时间延迟进行估计和补偿有待于进一步的研究。

[1]朱昀炤,汪顺亭,缪玲娟,等.船体变形测量技术综述[J].船舶工程,2007,29(6):58-61. Zhu Yunzhao,Wang Shunting,Miao Linjuan,et al.Hull deformation measurement technique were reviewed[J].Ship Engineering,2007,29(6):58-61.

[2]Alan M S.Kalman filter formations for transfer alignment of strapdown inertial units[J].Navigation,1983,30:72-89.

[3]Mochalov V,Kazantsev A V.Use of the ring Laser units for measurement of the moving object deformation[C].Proceedings of SPIE,2002.

[4]Dr Dana L,Day John Arruda.Measuring structural flexure to improve precision tracking[R].ADA 364862,1999.

[5]Mochalov A V.A system for measuring deformation of large-sized objects[C]//RTO/NATO.France,1999:15.1-15.9.

[6]Dr Dana L,Day Lockheed Martin.Measuring structural flexure to improve precision tracking[R].ADA364862,1999.

[7]Lyou Joon1,Lim You-Chol.Transfer alignment error compensator design based on robust state estimation[J].Trans.Japan Soc.Aero.Space Sci.,2005,48(161):143-151.

[8]李金石,秦石乔,王省书.船体形变惯性测量方法研究[J].计算机工程与应用,2008,33S:356. Li Jinshi,Qin Shiqiao,Wang Shengshu.The hull deformation inertial measurement method research[J].Computer Engineering and Applications,2008,33S:356.

[9]黄国刚,戴洪德,陈 明.快速传递对准中时间延迟误差补偿方法[J].测控技术,2009,28(8):55-57. Huang Guogang,Dai Hongde,Chen Ming.In the rapid transfer alignment time delay error compensation method[J].Observation and Control Technology,2009,28(8):55-57.

[10]徐 林,李世玲,屈新芬.三种传递对准延时误差补偿方法的比较研究[J].兵工自动化,2011,30(2):22-25. Xu Lin,Li Shilin,Qu Xinfen.Three types of comparative study of transfer alignment delay error compensation method[J]. Ordnance Industry Automation,2011,30(2):22-25.

[11]朱昀炤,汤霞清,李振伟.惯性测量匹配法测定船体变形实施方案研究[J].火力与指挥控制,2008,33:94-97. Zhu Yunzhao,Tang Xiaqing,Li Zhenwei.Inertial measurement matching method of hull deformation plan research[J].Fire Control&Command Control,2008,33:94-97.

[12]柳爱利,卢 伟.甲板变形测量技术研究[J].海军航空工程学院学报,2009,24(20):178-180. Liu Aili,Lu Wei.Study of deck deformation measurement technique[J].Journal of Naval Aeronautical Engineering Institute,2009,24(20):178-180.

A time delay compensation method based on the hull deformation measurement technology by FGU

XU Bo,CHEN Chun,SHI Hong-yang,GUO Yu
(College of Automation,Harbin Engineering University,Haerbin 150001,China)

The ship deformation measurement technology basing on the angular rate matching method by Fiber Gyro Unit has a time delay problem in practical applications by the real ship experiments.This paper analyses the reason of causing time delay,and puts the time delay factor into the deformation angle model proposed by Mochalov who is from Russia,and studies what effects can be make on estimating the deformation of ship by simulation.A time delay compensation method is proposed.After conducted an experiment of measuring the ship deformation,many data of ship measurement are obtained.By using the time delay compensation method,the measurement accuracy of the angular rate matching method can be improved. This paper is helpful for the practical application of the hull deformation measurement technology.

deformation of the hull;angular rate matching method;time delay;

TN967.2

A

10.3969/j.issn.1007-7294.2015.10.008

1007-7294（2015）10-1235-10

2015-01-30

中央高校基本经费项目（HEUCFQ20150408）；国家博士后基金（2012M510083）；国家自然科学基金课题（61203225）；黑龙江省自然科学基金（QC2014C069）

徐 博（1982-），男，博士研究生，讲师，E-mail:xubocarter@sina.com；

陈 春（1988-），男，硕士，E-mail:chenchun@hrbeu.edu.cn。