球体波能转换装置捕获能量的理论研究

张显涛，杨建民，肖龙飞

（上海交通大学海洋工程国家重点实验室，上海200240）

球体波能转换装置捕获能量的理论研究

张显涛，杨建民，肖龙飞

（上海交通大学海洋工程国家重点实验室，上海200240）

球体波能转换装置在波浪的激励下可以同时在水平和竖直两个模式振荡。基于线性微幅波浪和势流理论，将波浪与球体相互作用简化为球体固定不动，波浪绕过球体和球体在静止流体中运动。线性叠加以后得到总的速度势，计算出球体波能转换装置的平均功率和能量俘获宽度因子的解析表达式。理论研究表明：装置与波浪运动的相位差是影响波能的最重要的参数，最优相位差为-π/2，并且给出了最优相位差调节的理论表达式。另外，对波长、波幅、球体半径、水深和球心距静水面的距离等因素也进行了分析。

球体波能转换装置；理论研究；平均功率；能量俘获宽度因子；影响因素

0 引言

相对于风能，波能蕴含更高的能量密度，是很有前景的新型能源。但是，由于海洋环境的复杂性，通常认为波浪能的利用比风能晚了二十年，而且扩张性发展会在2030年左右[1]。

波能发电装置据其工作原理可分为振荡水柱式，振荡浮体式和收缩坡道式三种，Falcao[2]对此有比较详细的介绍。振荡浮体式是研究较多的一种装置，波能的捕获是利用装置的振荡。浮子式波能转换装置主要是利用浮子的垂荡运动。近岸振荡浮体波能转换装置是利用横荡运动。本文研究的球体波能转换装置充分利用其与波浪相互作用的横荡与垂荡运动，从而可以获得更高的能量。振荡浮体式波能转换装置与波浪相互作用研究的方法通常是数值计算和模型试验。Li Ye和Yu Yi-Hsiang[3]总结了数值计算的方法有格林函数法，基于势流理论的Morison方程求解粘性力，以及基于CFD的求解Navier-Stokes方程的方法。Babarit等人[4]对很多振荡浮体式波能转换装置进行了数值计算，以期给数值计算提供一个参考标准。Orer和Ozdamar[5]对板式波能转换装置进行了实验探究。Flocard等[6-7]对波浪中垂直柱体的纵摇运动的波能捕获进行了实验探究。

本文采用与数值计算和实验探究不同的方法，即对球体波能转换装置采用理论分析的解析方法，研究了装置在波浪作用下，同时发生横荡和垂荡两种运动模式下的波能捕获情况，推导了球体捕获的平均功率和波能俘获宽度因子，分析相对运动相位偏差、波长、波幅、水深、球体半径等参数对捕获能量的影响。

1 波能转换装置描述

本文研究的球体波浪能转换装置位于水面以下，可以同时在水平和垂向振荡，通过液压泵将机械能进一步转化成电能。球体波能转换装置与波浪的相互作用如图1所示。图中标出了球体的位置和尺寸。球体的半径为R；球心位于静水面以下，距离为h；水深为H；规则波的幅值为A，波长为λ。球体在波浪作用下的水平速度为U（t），垂向速度为V（t）。本文的目的是基于线性波浪理论，计算球体上的水平力FH（t）和垂向力FV（t），然后计算平均捕获能量P和能量俘获宽度因子ζcapture。忽略粘性力的作用，粘性力作为一种耗散力，认为本文计算的结果作为能量捕获的一个上限，粘性力的作用会使能量捕获有所减少。

2 波能转换装置与波浪的相互作用

2.1 线性波浪和势流理论

当波浪的幅值与波长之比A/λ＜＜1时，可以认为波浪是线性的。线性微幅波浪（Airy波）假设下，沿x方向传播的行进波在有限水深的速度势[8]为

其中：φ是流体的速度势，A是波幅，g是重力加速度，w是波浪的圆频率，H为水深，y是距离静水面的距离。k是波数，定义为k=2π/λ。

势流理论是在忽略流体粘性的情况下得到了有关流体运动和动力的理论。在理想流体的假设下，存在速度势的拉普拉斯方程，

令u为水平速度，v为垂向速度，则速度势满足，

在球坐标系中，不妨设速度势为φ（r,θ,β），则有

2.2 球体与波浪相互作用下流场的总的速度势

波浪与物体相互作用分为两个子问题[9]，物体在波浪中静止不动，入射波对物体发生作用，这部分的速度势分别是入射势和绕射势；物体在静水中以入射波浪的频率发生振荡，没有入射波，这部分的速度势称为辐射势。两种情况下的三种速度势线性叠加得到物体与波浪相互作用的流体总的速度势。

本文基于这种处理方法，对球体波能转换装置与波浪的相互作用简化，一是假定球体不动，水平和垂直来流绕过球体；二是假定球体在静水中做水平和垂直运动。Newman[8]运用分离变量法对来流绕过球体的速度势进行求解，给出以速度U的来流绕过固定的半径R的球体的速度势φ为

半径为R的球体在静水中以速度U做运动，其流场的速度势为

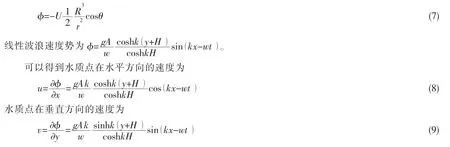
首先假定球体固定不动，分别有速度为u的水平来流和速度为v的垂直来流绕过球体波能转换装置，依据（6）式可得速度势

其中：当球体的尺寸相对于波长而言是一个小量时，设球体运动的幅值与水质点响应方向上运动的幅值相等，但是存在一个相位差φ，球体运动的水平和垂向速度分别为：

将两种情况下的速度势进行线性叠加可以得到，球体波能转换装置与波浪相互作用下流场总的速度势

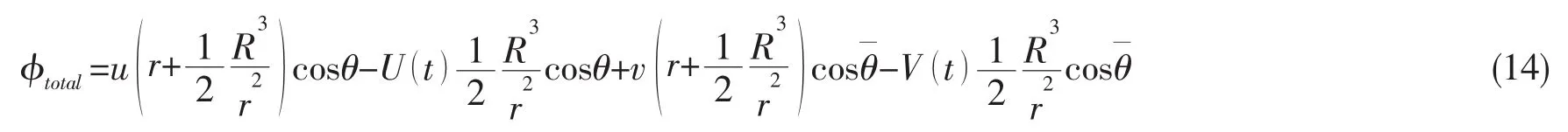
可以验证流场中总的速度势是满足球体坐标系下的拉普拉斯方程的，即φtotal满足

2.3 波浪对球体波能转换装置的作用力

非定常场中表征流场动力的伯努利方程为

其中：C（t）是与时间有关的常量，不妨将C（t）放到速度势φ中得到齐次的伯努利方程：

依据（17）式，可以得到

依据（15）式，可以得到

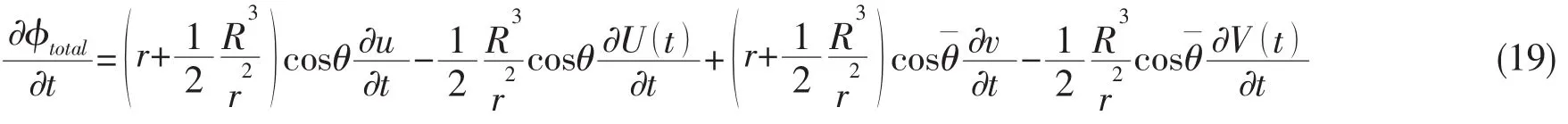
球心的坐标为（0，-h），球体的半径为R，以球心上的速度值来近似表示整个球面上的速度值，则有

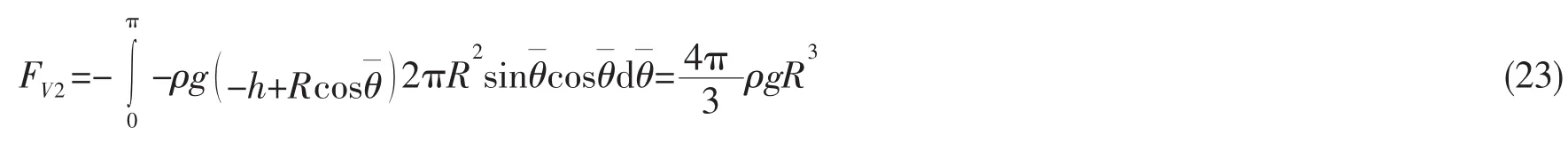
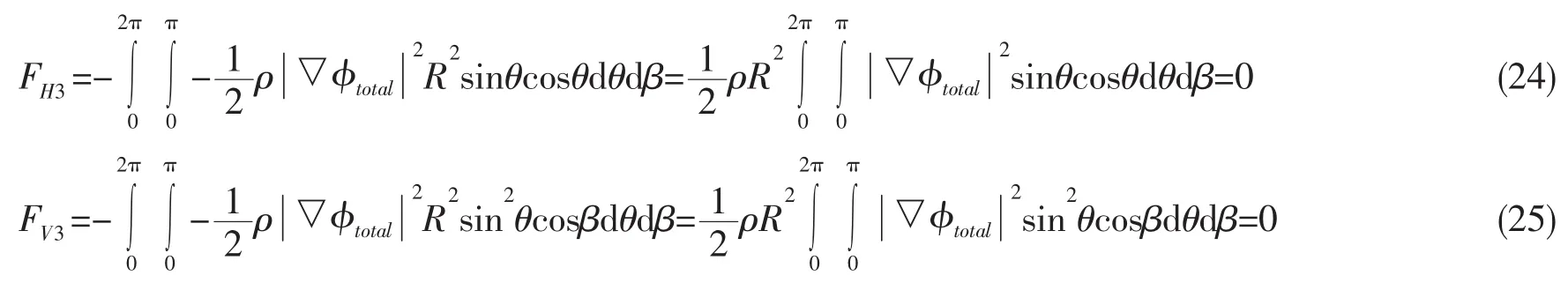
综上可得，作用在波能转换装置的总水平力为FH，总垂向力为FV：

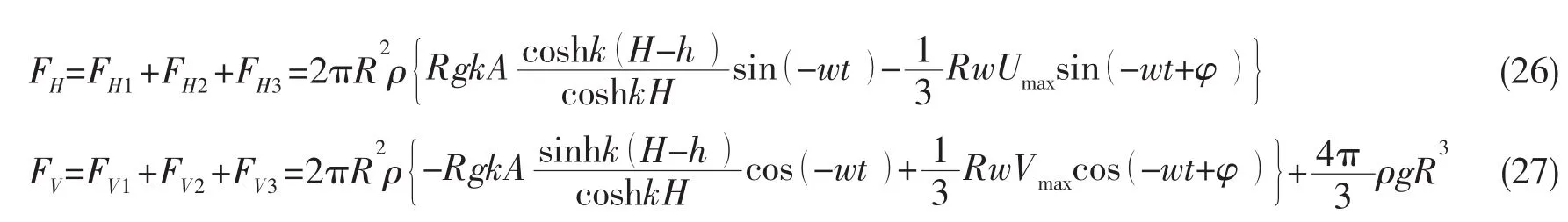
2.4 球体波能转换装置在波浪中的平均捕获能量和能量俘获宽度因子

依据（26）式和（27）式可以计算球体波能转换装置在一个波浪周期内的平均捕获能量为

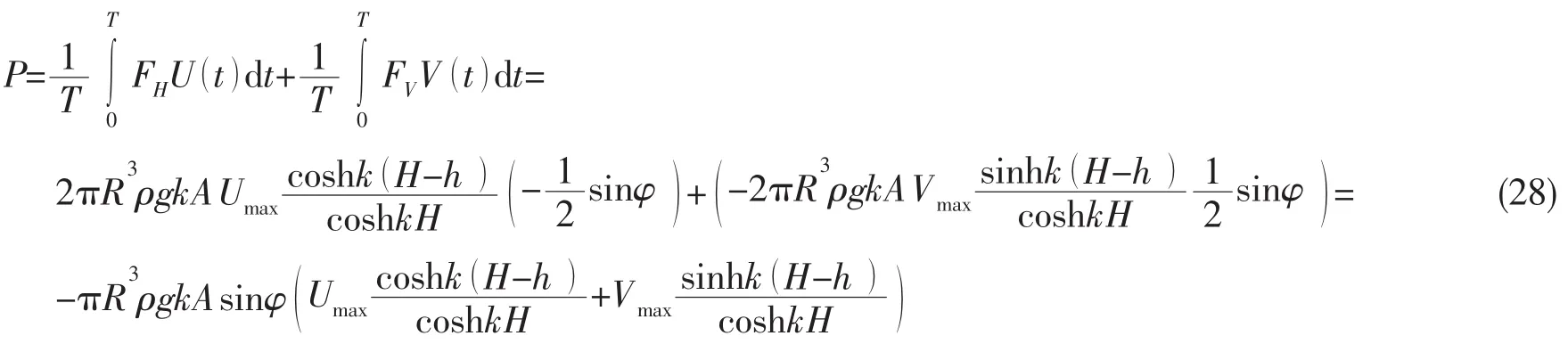
Newman[8]给出了单位波峰长度下，单位时间内，波浪的传递功率为

其中：Vg为波群速，VP为波浪的相速度，

波能转换装置的能量俘获宽度因子ζcapture定义为转换装置的捕获能量与波浪的传递功率和转换装置在垂直波浪传播方向上的尺度之积的比值[10-11]，即

这里假定球体的水平方向的运动速度幅值Umax，垂向的运动速度幅值Vmax分别与水质点的水平方向的速度幅值和垂向的速度幅值相等，即：

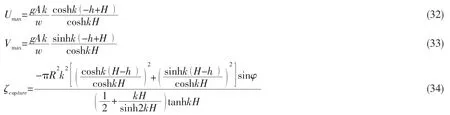
当水深H→∞时，有能量俘获宽度因子的表达式

3 波能转换装置的平均捕获能量和能量俘获宽度因子的影响因素分析

3.1 波能转换装置与波浪之间运动的相位偏差对能量俘获宽度因子的影响

波能转换装置与波浪之间的运动相位差是影响平均捕获波能和波能俘获宽度因子最重要的因素。在有限水深的情况下，（34）式表明当相位偏差φ为时，能量俘获宽度因子达到最大值，即最优相位差为此时球体运动与所受的波浪力同相位，这时功率最大。而且波能转换装置的捕获能量的相位差的有效区间为（-π，0），在这个区间内，能量俘获宽度因子是正值，波能转换装置的运动是比水质点的运动超前的。当相位差位于区间（0，π）时，波能转换装置的运动比水质点落后，这时捕获的能量是负值，是无效区间。

为了得到最优相位差，对波能转换装置的运动控制是必要的[12]。在初始布置球体波能转换装置时，控制其相位差的初始值为，其运动的圆频率是w0，在实际情况下，外界波浪的频率发生变化变成w（t），那么通过直接或间接对波浪周期的测量，利用负反馈，依据下式进行相位差的实时调节：

这样，可以保证波能转换装置的运动始终保持一个最优相位差，获得最大的能量捕获。在具体的实现过程中，因为相位调节需要外部能量的输入，即存在能耗。因此要综合权衡相位调节后的最大捕获能量与调节需要的输入能量，使净捕获能量达到一个最优值。

3.2 其他因素对能量俘获宽度因子的影响

在有限水深的情况下，依据（34）式，其他影响能量俘获宽度因子的因素主要有波数k，球体半径R，水深H，球体球心与静水面距离h等四个因素。下面将四个影响参数进行无量纲化，即可以得到三个影响能量俘获宽度的无量纲因素，

图2 水深对能量俘获宽度的影响，在kR=0.314，kh=0.314Fig.2 The influence of water depth on the ratio of power capture width

图3 圆柱半径R和球心距离静水面距离h对能量捕获宽度的影响Fig.3 The influence of sphere radius R and distance h on the ratio of power capture width

取波长λ=100 m，球体半径R=5 m，球心与静水面距离为h=5 m，在最优相位差时，得到水深对能量俘获宽度因子的影响如图2所示，可以发现，水深增加，能量俘获宽度因子ζcapture增大，但增长变慢，当kh≥4.5时，能量俘获宽度因子ζcapture逐渐趋于一个稳定值。水平线代表应用（36）式计算得到的结果。一般来讲，水深越大，能量俘获宽度越大，但是当水深大致超过波长的一半时，水深对能量俘获大小的影响可以忽略。因此在实际布置波能转换装置时，要选择一个适当的水深，以追求能量获取较大和维护控制经济可行的一个较优的水深选择。下面假设在深水情况下，在最优相位差时，讨论球体的半径R和球心距静水面的距离h对能量捕获宽度的影响。由图3，球体波能转换器半径R的增大，能量捕获宽度因子ζcapture增大，开始增加较慢，后来增加较快。在实际海况下，波能转换装置的尺寸选取还要考虑结构强度，共振区间和维护的成本等。因此，实际选取尺寸时，尺寸并非越大越好。球体球心距离静水面距离增加，能量捕获宽度因子减小，在距离较小时，能量捕获的减小较慢，但随着距离的增加，能量捕获宽度因子会出现较大幅度的减小，如图3中kh=0.754 0时的曲线明显偏离了其他几组曲线。所以目前研究较多的浮体式波能发电装置基本都是浮在水面上的。在水面以下的装置虽然能量的捕获变小，同时可减小外界波浪力对结构破坏作用，但选择时要综合考虑能量捕获和结构安全性与维护成本。

从（34）式和（35）式可以看到，波浪幅值对于能量俘获宽度因子没有影响，但波浪幅值的平方对应能量的大小[13]，因此波浪的幅值对于波能转换装置捕获平均能量有较大的影响，这点可以从（28）式看出。波能转换装置捕获到的平均能量是和波幅的平方成比例的。

4 结论

本文在线性微幅波浪和势流理论的假设下，推导了球体波能转换装置在水平和竖直两个模式振荡下平均捕获能量和能量俘获宽度因子解析表达式，基于推导结果对影响波能装置能量俘获宽度因子的因素进行讨论，获得结论总结如下：

（1）推导了球体波能捕获装置在有限水深和无限水深中能量俘获宽度因子的理论表达式，并给出了球体运动与波浪的水质点运动最优相位差的调节的理论公式。

（2）水深增加，能量俘获宽度因子增大，但是增长的速度逐渐变慢，当水深超过波长的一半时，水深对能量俘获大小的影响可以忽略。

（3）随球体波能转换装置半径的增大，能量捕获宽度因子也增大，刚开始增加得比较慢，后来增加得较快。球体距离水面的距离的增加会导致能量俘获宽度因子的减小，实际设计时，应选取浮在水面上的波能发电装置。

（4）波幅的大小对于能量俘获宽度因子没有影响，但是对装置捕获的能量大小有较大的影响。

[1]European Ocean Energy Association(EU-OEA).Oceans of energy-European ocean energy roadmap[Z].2010:2010-2050.

[2]Falcao A F de O.Wave energy utilization:A review of technologies[J].RENEW SUST ENERG REV,2009,14(3):899-918.

[3]Li Ye,Yu Yi-Hsiang.A synthesis of numerical methods for modeling wave energy converter-point absorbers[J].RENEW SUST ENERG REV,2012,16(6):4352-4364.

[4]Babarit A,Hals J,Muliawan M J,et al.Numerical benchmarking study of a selection of wave energy converters[J].Renewable Energy,2012,41:44-63.

[5]Orer G,Ozdamar A.An experimental study on the efficiency of the submerged plate wave energy converter[J].Renewable Energy,2007,32(8):1317-1327.

[6]Flocard F,Finnigan T D.Laboratory experiments on the power capture of pitching vertical cylinders in waves[J].Ocean Engineering,2010,37(11-12):989-997.

[7]Flocard F,Finnigan T D.Increasing power capture of a wave energy device by inertia adjustment[J].Applied Ocean Research,2012,34:126-134.

[8]Newman J N.Marine hydrodynamics[M].United States:MIT Press,1977:111-127.

[9]Faltinsen O M.Sea loads on ships and offshore structures[M].Cambridge:Cambridge University Press,1990:39-41.

[10]Falnes J.Ocean waves and oscillating system[M].Cambridge:Cambridge University Press,2002.

[11]Price A A E,Dent C J,Wallace A R.On the capture width of wave energy converters[J].Applied Ocean Research,2009, 31:251-259.

[12]Heikkinen H,Lampinen M J,Boling J.Analytical solution of the interaction between waves and cylindrical wave energy converters oscillating in two modes[J].Renewable Energy,2013,50:150-160.

[13]刘应中,缪国平.高等流体力学[M].上海:上海交通大学出版社,2002.

Analytical study of power capture of spherical wave energy converts in two modes

ZHANG Xian-tao,YANG Jian-min,XIAO Long-fei
(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

A floating spherical wave energy converter submerged under the water surface is studied.The converter can oscillate in both horizontal and vertical modes induced by waves and transfer mechanical energy forward by hydraulic cylinders.Based on the linear potential theory of airy waves,the interaction of the waves and the wave energy converters can be divided into two parts.One is flow past a fixed spherical body. The other is a spherical body moving in fluid at rest.By linear superposition of the two parts of velocity potential,the final velocity potential is achieved.Then the time-averaged power capture and power capture width ratio is calculated.Different parameters that affect the efficiency of wave energy harvesting are analyzed.The optimal phase difference between the motion of converters and water particles is obtained with a value of-π/2.And phase control is needed to keep the optimal phase difference for different waves.The radius of the spherical body,the wave length and wave amplitude and water depth,as well as the distance of the center of the wave energy converter from the surface,have effects on the efficiency of power capture.

spherical wave energy converter;analytical study;time-averaged power; power capture width ratio;influence factor

P751

A

10.3969/j.issn.1007-7294.2015.04.001

1007-7294（2015）04-0349-07

2014-10-26

张显涛（1991-），男，硕士生，E-mail:zhxter@outlook.com；杨建民（1958-），男，教授，博士生导师。