一种基于RS码的宽间隔跳频序列生成方法

罗 翔，周三文，焦东立，韩一学

（1北京遥测技术研究所 北京 100076 2西安卫星测控中心 西安 710043）

引 言

跳频通信的主要特征是其载波频率在伪随机序列的控制下，不断在特定的频率范围内跳变，从而达到抗干扰、抗截获等目的。控制载波频率跳变的伪随机序列称为跳频序列，跳频序列性能的好坏对于跳频系统的抗干扰性能有着决定性影响[1]。

通常设计跳频序列时应考虑以下几个要求：跳频序列能够使用频率集合中的所有频率，以实现最大的处理增益；跳频序列应具有良好的汉明相关性；为实现多址和保密通信，要求跳频序列集合中的序列数目尽可能多；为使跳频系统具有良好的抗干扰性能，应使各频点在一个序列周期中均匀出现[2]；为保证跳频图案具有不可逆推性和较强的抗破译性，跳频序列应具有较高的随机性和复杂度[3]。

常用于生成跳频序列的伪随机序列主要有m序列、M序列、GOLD序列和RS码等。其中RS码与其他伪随机序列相比具有以下优势：RS码是一种最佳的近似正交码，具有很好的互相关性；与同样长度的m序列相比，RS码可供选择的码数更多；RS码是最小距离最大码（MDC），该性质对于构造性能较好的宽间隔跳频序列极其有利，是其他许多伪随机序列所不具备的；RS码的硬件实现也较简单。因此以RS码生成跳频序列是一种适宜的选择[4]。早在20世纪60年代国外就有学者提出利用扩展RS码构造跳频序列族[5]。

文献[4]直接用RS（63，2）码作为跳频序列，控制126个频点的跳变（采用对偶频带法进行宽间隔处理）。这种非重复跳频序列的互相关性很好，但由于一个跳频周期内每个频点最多出现一次，受实际工程中频点数目的限制，跳频周期不可能太长。文献[3]提出了跳频序列复杂度的两方面衡量标准，一是产生伪随机序列的移位寄存器的长度，二是从伪随机序列到跳频序列之间非线性变换的复杂度。由此可得，非重复跳频序列的复杂度较低，抗干扰性和抗破译性较差，工程实用性不强。目前大部分类似的文献中，基于RS码生成的跳频序列都是非重复的，其周期一般不大于1023，因而复杂度较低。本文针对该方案的缺点进行如下改进：一方面使用周期更长的RS码，另一方面使用非线性转移矩阵法将RS码转换为跳频序列，大大增加了跳频序列的复杂度，并用对偶频带法对其进行宽间隔处理，通过仿真证明了其良好的均匀性、随机性和汉明相关性。

1 RS码的基本原理及其产生方法

RS码是一种长度（周期）为N=q-1的q元域BCH循环码，符号取自GF（q），其中q=pm，p为素数。若RS码能纠正t个错误，则长度为N的RS码由b个信息位和2t个纠错位组成，记作RS（N，b）。RS（N，b）码字间的最小距离最大值d=N-b+1，其最大重合分量k=b-1，它是最佳的k次近似正交码[6]。

设有b个信息位、定义在GF（q）上的RS码是如下生成矩阵的向量空间：

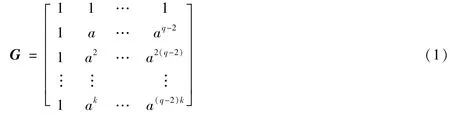
式（1）中，a为GF（q）的本原元，k=b-1为最大重合次数。我们假设信息元向量为V=[v0，v1，…，vb-1]，则RS码字向量为：

当b=2时，RS（N，2）性能最好[4]，它是一种近似正交码，可以构造出最佳的RS跳频图案，保证在任何跳频时延下，任意两条跳频序列在一周期内的频点重合次数不大于1。RS码的周期越长，其构造的跳频图案性能越好，但同时也会增加仿真与实现的复杂度，需要折中考虑。本文选择N=220-1=1048575，一方面是因为目前大部分基于RS码生成的非重复跳频序列周期一般不大于1023，选20个移位寄存器既大大增加了序列周期又保证了较低的仿真实现复杂度；另一方面是因为后文要将RS码转换成5bit的跳频序列，移位寄存器的个数取5的整数倍可以方便转换且保证了跳频序列的均匀性。GF（1048576）上的RS（1048575，2）码的码字向量为：

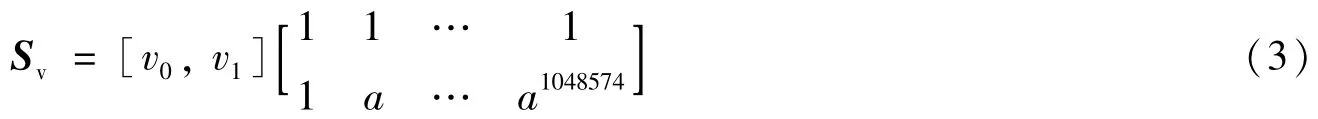
设v0=0，v1=1，则所生成码字为[1，a，a2，…，a1048574]，跳频码的计算就转化为GF（1048576）中1048575个元素的计算。GF（1048576）中本原元a的最小生成多项式为f（x）=1+x3+x20，根据伽罗华域中元素运算法则，可推算出域中的1048575个元素。

通过观察容易得出以下规律，当an-1最高位为0时，an由an-1循环左移得到；当an-1最高位为1时，将an-1第20位（最高位）和第3位模二加并将结果送入an的第4位，an的其它位由an-1的相应位循环左移得到。根据a的最小生成多项式也容易得出RS（1048575，2）码的编码电路如图1所示。

RS（1048575，2）码可直接作为跳频序列控制载波的伪随机跳变。但该方法控制的跳频频点数必须为1048575，这在实际中显然无法实现，必须对其做出一些改进。

图1 RS（1048575，2）码的编码电路Fig.1 The coding circuit of RS（1048575，2）

2 改进的RS码宽间隔跳频序列的设计方法

前文所述的长周期RS码增加了跳频序列的复杂度，但其在实际工程中无法直接实现。本节采用非线性转移矩阵法将较长的RS码转换为较短的跳频序列，该算法不仅进一步增加了序列复杂度，而且使其易于在工程中实现。同时为了增加序列的抗干扰性，采用了对偶频带法对其进行宽间隔处理。

2.1 高复杂度RS码跳频序列的简单实现方法

根据引言所述的跳频序列复杂度的两方面衡量标准[3]，文献[4]及大部分类似文献中产生RS码非重复跳频序列的移位寄存器个数一般不超过10，而本文产生RS码的移位寄存器个数为20，复杂度大大增加。文献[4]等直接将RS码作为跳频序列，没有非线性转换过程，本文为了进一步提高复杂度，采用非线性转移矩阵法，将20bit的RS码右乘一个20行5列的矩阵，将其非线性转换为5bit的跳频序列：

式（4）中L1×20表示20bit的RS码，T20×5表示非线性转移矩阵，N1×5表示5bit的跳频序列。非线性转移矩阵法的复杂度定义为非线性转移矩阵的行数、列数之积[3]，在本方案中为100，即经过非线性转移矩阵转换后序列的复杂度增大了100倍。构造适当的非线性转移矩阵至关重要，它直接影响到所生成的跳频序列的均匀性。文献[7]中指出，若非线性转移矩阵T20×5具有非奇异性，即T20×5的秩为5，则能够保证转换后跳频序列的遍历性和均匀性。本文据此提出了一种非线性转移矩阵法的简单实现方法，如图2所示。

为保证非线性转移矩阵的秩为5，将图1中的20个寄存器分成5组，每组中的4个寄存器都是等间隔抽取的：R0、R5、R10、R15为一组，R1、R6、R11、R16为一组，以此类推……分别将每组4个寄存器的值模二相加，得到5bit序列，再将其与输入的5位信息向量V作模二加，并将得到的5位二进制数q0至q4作为跳频序列，去控制频率控制字的跳变。该算法实现简单，且较好地保证了转换后跳频序列的遍历性和均匀性。

图2 一种基于RS（1048575，2）码的跳频序列产生方法Fig.2 A method of the generation of FH sequences based on RScode

2.2 RS码宽间隔跳频序列的生成算法

实际的跳频系统通常要求实现宽间隔跳频。宽间隔跳频是指在相邻的跳频时隙里发射的两个载波的频率间隔大于某个规定的值，这一要求首先是美国三军联合战术信息分发系统（JTIDS）提出的。对于已经确定跳速的系统来说，将跳频序列设计成宽间隔，有利于对抗单频窄带干扰、跟踪干扰和宽带阻塞式干扰，也有利于抗多径衰落。目前设计宽间隔序列的常用方法有去中间频带法和对偶频带法等[8]。

根据工程实践经验，本文将跳频频段定在1350MHz至1550MHz范围内。设相邻频点间隔3MHz，可在1356MHz至1545MHz间设置64个跳频频点。为使相邻跳频时隙的载波间隔大于30MHz，根据洪福明、张世平提出的对偶频带法[9]，可将64个频点分为左右对称各32个频点：F1=｛1356，1359，…，1449｝和F2=｛1452，1455，…，1545｝。设计如下的算法生成基于RS码的宽间隔跳频序列：按照图2所示算法，约定R0至R19的初始状态，信息向量V为定值，移位寄存器每移位一次代表一跳，设q4至q0表示的十进制值为Q，则Q的跳变范围为[0，31]，对应了F1上的32个频点。另设一个范围为[0，63]的变量Q′（依次对应上述64个跳频点），按照图3所示流程图完成宽间隔跳频序列的生成（图3中的i表示跳数，i≥1）。Q′即为最终的宽间隔跳频序列，通过Q′可控制频率控制字的伪随机跳变。

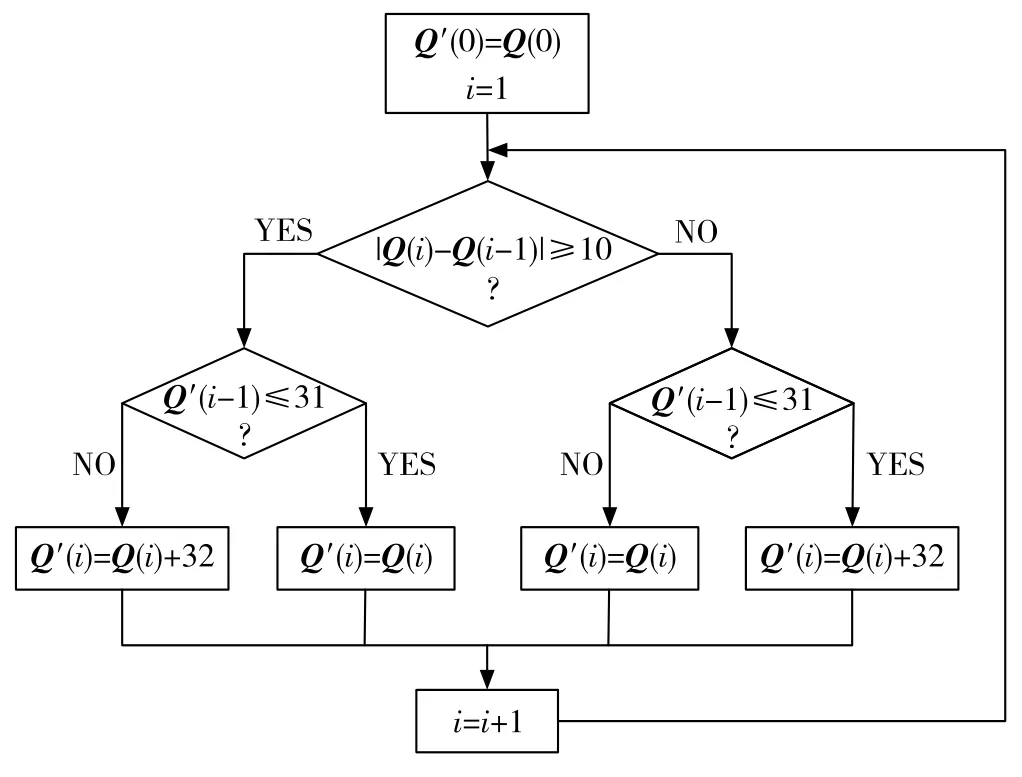
图3 宽间隔跳频序列产生流程图Fig.3 Flowchart of the generation of wide interval FH sequences

3 性能仿真

按照前文所述方法，设R19至R0的初始状态为10000000000000000000，V的取值有32种情况，对应了32条不同的跳频序列Q′1至Q′32。当V0至V4取00001时，可以仿真得到周期为1048575的Q1值，经过宽间隔跳频处理后，可得相应的宽间隔跳频序列：

Q′1=｛0，25，2，21，58，36，57，34，53，26，4，25，2，21，58，…，32，49，18，52，24，0，17，50，20，56｝

当V0至V4取00100时，可以仿真得到周期为1048575的Q2值，经过宽间隔跳频处理后，可得相应的宽间隔跳频序列：

Q′2=｛20，45，22，1，14，48，13，54，33，46，16，45，22，1，14，…，52，37，6，32，44，20，5，38，0，12｝

统计Q′1和Q′2一周期内每个跳频频点的出现次数，其结果图4所示。

图4 Q′1和Q′2一周期内每个跳频频点的出现次数Fig.4 The number of each frequency value in a period of Q′1andQ′2

由统计可得，Q′1一周期内出现最少的频点为53，次数为16236，出现最多的频点为21，次数为16532。Q′2一周期内出现最少的频点为45，次数为16208，出现最多的频点为13，次数为16560。所有频点的出现次数基本在平均值16384附近抖动，抖动率约为1%。根据数理统计原理，可以通过χ2拟合检验法检验跳频序列的均匀性。统计学上的显著性水平一般取0.05，提出假设H0：64个频点出现的概率相等。统计一个周期1048575内第i个频率出现的次数ni，根据式（5）可以计算出实际统计量p，将其与理论值进行比较，就能衡量假设与实际的符合程度。

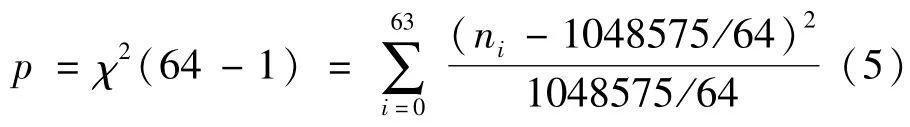
经计算可得，Q′1的实际统计量p1为16.6691，Q′2的实际统计量p2为25.2685，它们均远小于理论值χ20.05（64-1）=82.2447，说明在水平0.05下是可以接受假设H0的，即Q′1、Q′2具有良好的均匀性。通过类似的方法可检测出Q′3至Q′32也具有良好的均匀性。

跳频序列是一种伪随机序列，理论上伪随机序列的随机性越好，其自相关函数越接近冲激响应，其功率谱越平坦。周期为1048575的跳频序列Q′1的自相关函数可由式（6）计算：

其中

x

（

n

）为Q

′

1

的第

n

个元素，

m

为相对时延。仿真可得Q

′

1

的自相关函数如图5所示。

图5 Q′1的自相 关 函 数Fig.5 Curve of the auto-correlation function of Q′1

由图5可知Q′1的自相关函数比较接近于冲激响应，说明该跳频序列具有较好的随机性。

汉明相关性是衡量跳频序列性能的重要指标。汉明自相关表示跳频序列在相对时延下与自身的频点重合次数，汉明互相关表示两条跳频序列在相对时延下频点的重合次数，它们对跳频系统的抗干扰性能和多址组网性能有着重要影响。周期为L的跳频序列S在相对时延为τ时的汉明自相关值可由式（7）计算得到：

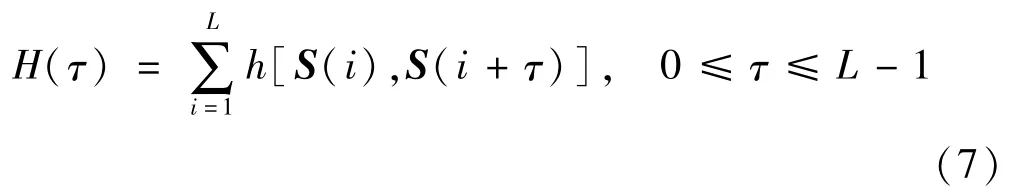
周期为L的两条跳频序列S1和S2在相对时延为τ时的汉明互相关值可由式（8）计算得到：

在式（7）与式（8）中：

仿真Q′1的汉明自相关性，结果如图6所示。由图6可知，当时延为0时，序列的汉明自相关达到峰值1048575，当时延不为0时，序列的汉明自相关值最大为32767，约为序列周期的3.1%，说明该跳频序列具有良好的汉明自相关性。同理，通过仿真可得Q′2至Q′32也具有良好的汉明自相关性。

仿真Q′1和Q′2的汉明互相关性，结果如图7所示。由图7可知，当时延为0时，Q′1和Q′2的互相关值为0，此时它们没有重合的频点；当时延不为0时，它们的汉明互相关值最大为16800，约为序列周期的1.6%。文献[10]指出，若跳频序列X、Y长度为2n-1，频点数目为2k，则序列X和序列Y之间的最大汉明互相关的最小值等于2n-k。在本文中，n为20，k为6，则任意两条跳频序列之间的最大汉明互相关的理论最小值为16384，实测结果16800与理论最小值非常接近，证明了其良好的汉明互相关性。在Q′3至Q′32中任取两条序列仿真其汉明互相关性，均可得类似的结果。

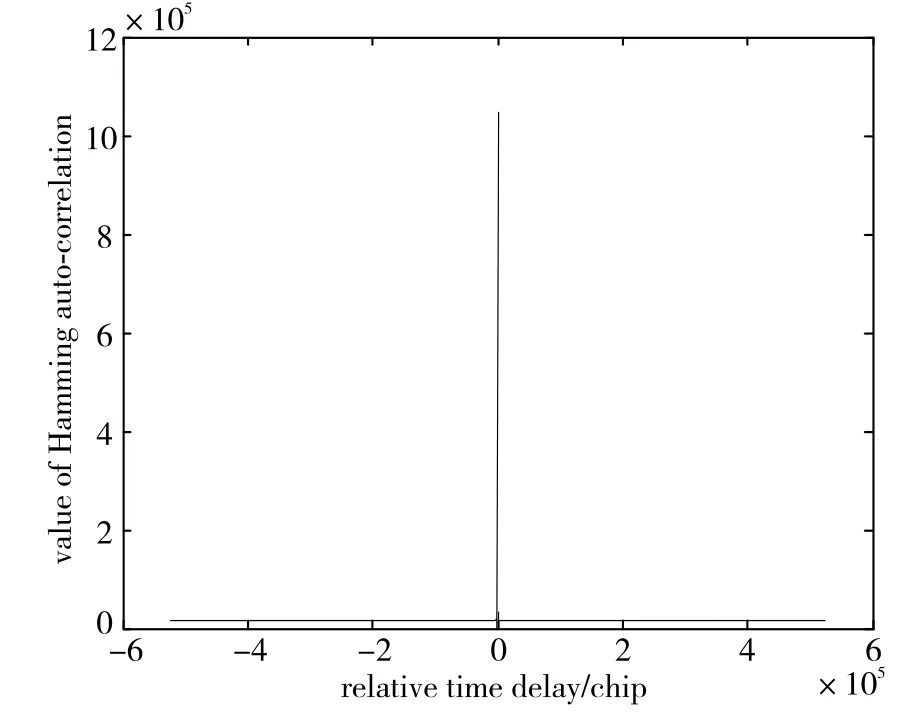
图6 Q′1的汉明自相关曲线图Fig.6 Curve of the Hamming auto-correlation of Q′1

图7Q′1和Q′2的汉明互相关曲线图Fig.7 Curve of the Hamming cross-correlation of Q′1 and Q′2

设计时已保证了相邻跳频频点的间隔不小于10，经仿真验证可得Q′1中相邻频点间隔的平均值为24.90，Q′2中相邻频点间隔的平均值为25.44，符合宽间隔跳频要求，说明该跳频序列具有较强的抗干扰性能。此外，改变信息向量V的值和图2中5个寄存器分组的排列组合方式，容易得到数目较多的跳频序列，实现多址跳频通信。综上所述，该序列基本满足前文所述的跳频序列的设计要求，能够实现较高的跳频性能。

4 结束语

本文在RS（1048575，2）码的基础上进行了一些改进，用非线性转移矩阵法完成对RS码的非线性转换，并采用对偶频带法对其进行宽间隔处理。与文献[4]的方案相比，该方案生成的跳频序列周期更长，序列复杂度大大提高，抗干扰性和保密性更强，具有更好的工程实用性。经仿真分析，该方法产生的宽间隔跳频序列在增加了复杂度的情况下，仍具有良好的均匀性、随机性和汉明相关性，且实现较为简单。在实际工程中，若通过时间参数TOD与密钥PK的非线性运算来控制信息向量V，能够使跳频序列与时间信息对应起来，进一步增加跳频序列的复杂度以及跳频序列的数目。

[1]胡建凯，曾兴雯.扩频通信系统中跳频图案的设计实现[J].无线通信技术，2002，11（2）：34～37.Hu Jiankai，Zeng Xingwen.The Design and Realization of Frequency Hopping Patterns in Spread Spectrum Communication Systems[J].Wireless Communication Technology，2002，11（2）：34～37.

[2]王育红.一种基于RS码的跳频码序列的编写方法[J].遥测遥控，2002，23（3）：11～14.Wang Yuhong.A New Method of Encoding FH Sequences Using RS Code[J].Journal of Telemetry，Tracking and Command，2002，23（3）：11～14.

[3]姚富强.通信抗干扰工程与实践[M].北京：电子工业出版社，2012.Yao Fuqiang.Communication Anti-jamming Engineering and Practice[M].Beijing：Publishing House of Electronics Industry，2012.

[4]徐定杰，赵彦雷，尹荣荣，赵彦明.基于RS码的宽间隔跳频序列设计[J].应用科技，2010，37（2）：28～33.Xu Dingjie，Zhao Yanlei，Yin Rongrong，Zhao Yanming.The Design of Wide Interval FH Sequences Based on RSCode[J].Applied Science and Technology，2010，37（2）：28～33.

[5]Wu Gang，Wang Ding.Design and Performance Investigation on Frenquency Hopping Sequence with Minimum Gap Based on RSCode[C]//International Conference on Electrical and Control Engineering，2010：5120～5123.

[6]Mao Fulin，Guu Changyang，Cheng Yuanchang.Frenquency-Hopping CDMA with Reed-Solomon Code Sequences in Wireless Communications[J].IEEE Transactions on Communications，2007，55（11）：2051～2055.

[7]李 赞，金立军，常义林.一种快速的跳频序列产生方法[J].西安电子科技大学学报，2001，28（2）：150～153.Li Zan，Jin Lijun，Chang Yilin.A Fast Generation of Frequency Hopping Sequences[J].Journal of Xidian University，2001，28（2）：150～153.

[8]Kumar P V.Frequency-Hopping Code Sequence Designs Having Large Linear Span[J].IEEE Transactions on Information Theory，1998，55（11）：146～151.

[9]洪福明，张世平.宽间隔跳频图案的探讨[J].成都电讯工程学院学报，1985，（S2）：6～12.Hong Fuming，Zhang Shiping.A Study of Hopping Patterns with Broad Interval[J].Journal of Chendu Institute of Radio Engineering，1985，（S2）：6～12.

[10]梅文华，杨义先.跳频通信地址编码理论[M].北京：国防工业出版社，1996.Mei Wenhua，Yang Yixian.The Theory of Frequency Hopping Communication Address Coding[M].Beijing：National Defence Industry Press，1996.