基于航空光电侦察平台的目标测速*

徐 诚，黄大庆，周春祎，韩 伟，王东振

（1南京航空航天大学无人机研究院 南京 210016 2南京航空航天大学电子信息工程学院 南京 210016）

引 言

利用航空光电侦察平台实现目标定位是指结合载机的导航信息以及光电侦察平台的测角、测距信息解算出地面目标的位置（经度、纬度、高度）。目前，国内外学者在基于航空光电侦察平台的目标定位理论和提高目标定位精度方面进行了研究和探讨[1～3]。随着科学技术的发展，仅对地面目标进行定位已不能满足信息全面化、动态化的需求，利用航空光电侦察平台实现空中对地面目标的测速已十分必要。

传统的对地面目标的测速采用机载雷达实现，而雷达测速主要是利用多普勒效应：当目标靠近雷达天线时，反射信号频率将高于发射机频率；反之，当目标远离天线而去时，反射信号频率将低于发射机频率。如此即可借由频率的改变数值，计算出目标与雷达的相对速度[4]。与雷达测速相比，利用航空光电侦察平台测速具有使用灵活、易于自身隐蔽的优点，可以作为雷达测速的一个有效补充。

本文对基于航空光电侦察平台的目标测速技术做出了研究，推导出一种便于部署、易于实现的目标测速方式。仿真结果证明，该测速方法是可行有效的，具有较高的应用价值。

1 系统构成与坐标系定义

1.1 系统总体结构

本文讨论的无人机目标测速系统装备了卫星接收机、惯性导航系统、光电侦察平台。机载光电侦察平台采用倒挂的方式安装在载机上，由于飞机在飞行过程中，飞机位置和姿态均在变化[5]，光电侦察平台的稳定跟踪功能可以隔离载体姿态运动和其他干扰力矩所造成的光轴在惯性空间内的抖动，以保证获取清晰的图像。在获取感兴趣目标图像后，光电侦察平台的图像跟踪器开始工作，保持目标位于摄像机视场中心，实现对目标的稳定跟踪，如图1所示。当对目标测速时，光电侦察平台的光轴指向角、无人机与目标的距离以及无人机的位置和姿态信息均可通过测量获取。

1.2 坐标系定义

首先，定义如下坐标系[5，6]：

（1）大地坐标系

大地坐标系是以地心作为原点，Zo轴为北极方向，Xo轴为地心指向格林尼治子午面与地球赤道的交点方向，Yo轴与Xo、Zo两轴相互垂直构成一个右手系。在大地坐标系中每一点的坐标可表示成（B，L，H），分别代表该点的纬度、经度、高程。

（2）大地直角坐标系

大地直角坐标系与大地坐标系重合。大地直角坐标系中任一点的坐标可用该点在此坐标系的各个坐标轴上的投影来表示：（xg，yg，zg）。

（3）地理坐标系

在地理坐标系中，原点是载机中心在某一时刻所处的位置，Zn指向正北方向，Xn垂直于地表指向天空，Yn与Zn、Xn相互垂直构成一个右手系，如图2所示。地理坐标系中每一个点的坐标可以表示为（xn，yn，zn）。

图1 目标测速系统示意图Fig.1 The diagram of target velocity measurement system

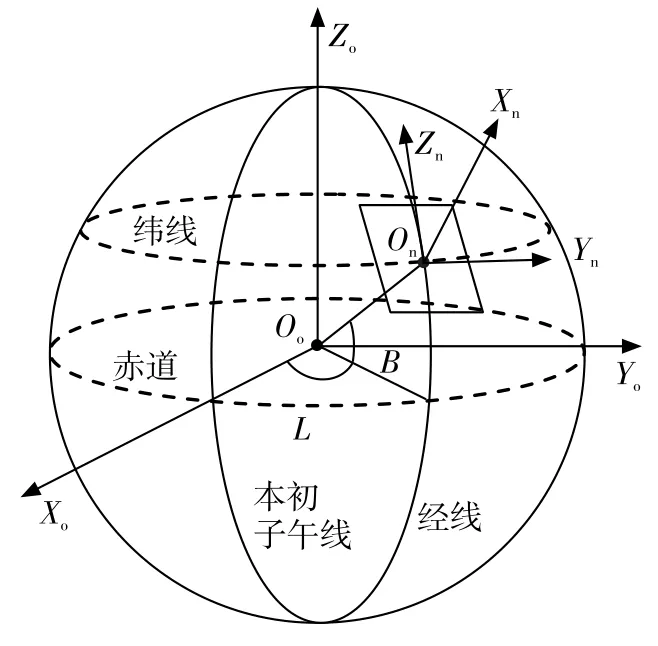
图2 坐标系定义Fig.2 Coordinate system definition

（4）载机坐标系

载机坐标系的原点为载机导航系统的中心，Yb代表载机横轴，Zb代表载机纵轴，Xb由载机腹部指向背部。载机航向角φ、俯仰角γ、横滚角θ代表该坐标系相对地理坐标系的三轴姿态角。当姿态角均为零时，载机坐标系的三轴指向与地理坐标系的三轴指向重合。在载机坐标系中任一点的坐标表示为（xb，yb，zb）。

（5）摄像机坐标系

摄像机坐标系的原点在摄像机光轴与横轴的交点上，Zc轴为摄像机光轴，指向目标。光轴指向角用方位角α、高低角β表示，其中方位角α为绕方位轴Xc的旋转角度；高低角β为绕俯仰轴Yc的旋转角度。

2 坐标变换

（1）从大地坐标系到大地直角坐标系的转换

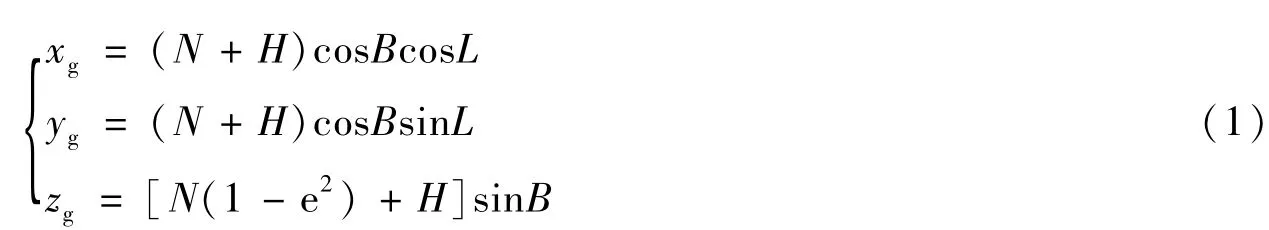
其中，N代表卯酉圈曲率半径，e代表椭球体的第一偏心率；a代表椭球体的长半径。

（2）从大地直角坐标系到地理坐标系的转换

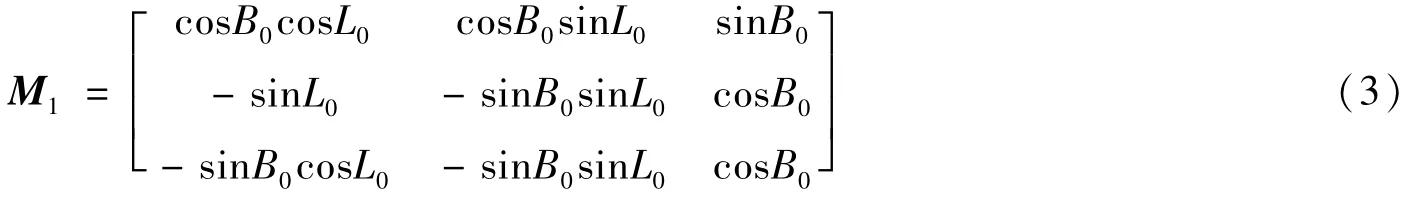
其中，[x0y0z0]T为地理坐标系坐标原点在大地直角坐标系中的坐标，L0、B0为地理坐标系坐标原点的经、纬度。

（3）从地理坐标系到载机坐标系的转换

绕X轴旋转φ的转换矩阵：

绕旋转后的Y轴旋转γ的转换矩阵：

绕旋转后的Z轴旋转θ的转换矩阵：

从地理坐标系到载机坐标系的转换如式（7）所示。

其中，φ、γ、θ分别为载机的航向角、俯仰角、横滚角，可由机载惯导系统测量获取。

（4）从载机坐标系到摄像机坐标系的转换

绕X轴旋转α的转换矩阵：

绕旋转后的Y轴旋转β的转换矩阵：

因此，从载机坐标系到摄像机坐标系的转换如式（10）所示。

α、β为摄像机的方位角和高低角，由光电侦察平台测量输出。

3 运动目标测速算法

光电侦察平台在跟踪运动目标的过程中，稳定跟踪装置可以使摄像机的光轴指向运动目标，保证运动目标位于摄像机视场中心。同时，载机的自身位置和姿态角由导航系统提供，摄像机方位角和高低角由光电侦察平台输出，载机与目标的距离由激光测距机测量获取。为了获取一定时间内目标运动的平均速度，需要运动目标的起点和终点位置以及时间间隔。因此，求取目标运动速度的关键是利用已知测量数据，求取目标起点和终点在同一参考坐标系下的坐标，具体问题描述如下：

（1）已知A时刻和B时刻的摄像机俯仰角、高低角以及目标相对载机的距离；

（2）已知A时刻和B时刻的载机经纬度、高程和载机三个姿态角；

（3）求A时刻到B时刻时间内目标在东向、北向、天向的平均速度。

选取A时刻目标的地理坐标系作为参考坐标系，如图3所示。将问题的求解分为以下四个步骤：

图3 参考坐标系Fig.3 The reference coordinate system

（1）求取A时刻目标在大地直角坐标系下的坐标以及纬度Ba、经度La和高度Ha；

坐标转换过程如图4所示。

图4 坐标转换过程Fig.4 Coordinate transformation process

则根据式（2）、（7）、（10），可得：

其中：

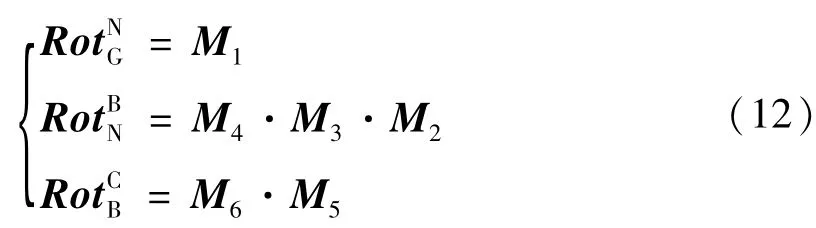
根据式（11），目标在大地直角坐标系下的坐标为：

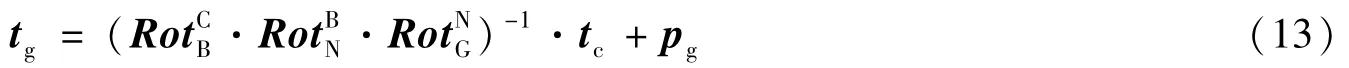
求得tg后，目标在大地坐标系下的坐标可通过文献[7]中方法求解。

（2）求取B时刻目标在大地直角坐标系下的坐标，求解方法同上；

由于选取A时刻目标的地理坐标系作为参考坐标系，因此此步骤本质上是将B时刻目标的大地直角坐标转换到A时刻目标的地理坐标系下，具体如式（14）所示。

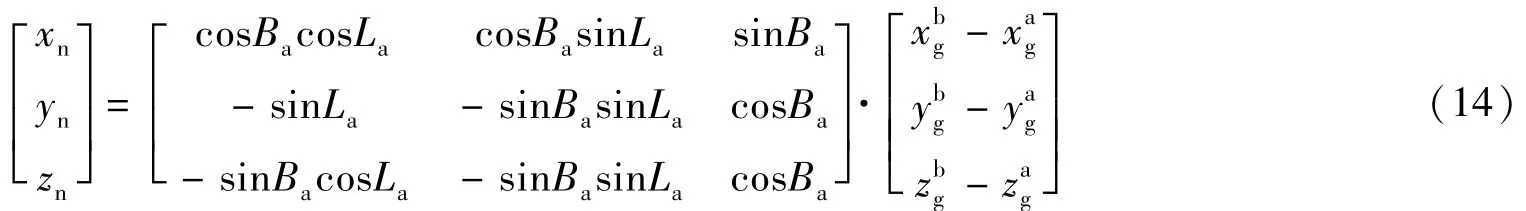
（4）求取目标在东向、北向、天向的平均速度。

设A时刻和B时刻的时间间隔为t，目标在参考坐标系下的平均运动速度为：

其中，vu、ve、vn分别为目标的天向、东向、北向速度。

4 测速误差模型

Monte-Carlo方法，又称统计试验方法或随机抽样方法，属于计算数学的一个分支，是一种基于“随机数”的计算方法。Monte-Carlo方法是在简单的理论准则基础上，采用反复随机抽样的手段，解决复杂的系统问题。Monte-Carlo方法的核心思想是：对于某个待求问题，构建一个合理的随机过程或概率模型，使得其参量（如事件的概率、随机变量的数学期望等）等于所求问题的解，然后对模型或过程进行反复多次的随机抽样试验，并对结果进行统计分析，最后计算所求参量，得到问题的近似解。

假设目标速度求解过程为：

则测速误差模型为：

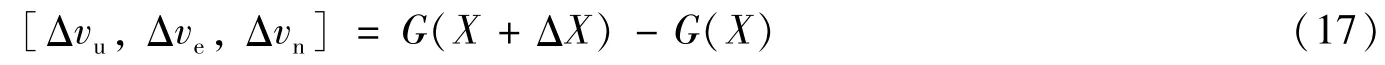
式中，Δvu、Δve、Δvn为目标速度误差；G为目标测速方程；X、ΔX分别为各测量参数的真实值和误差，包括：载机的经度、纬度、高程、航向角、俯仰角、横滚角，光电侦察平台的方位角、高低角以及激光测距值。

5 数值仿真及分析

设置目标的真实运动速度为：vu=0.5m/s、ve=12m/s、vn=12m/s，测速时间间隔为t=1s。载机自身定位误差5m，姿态角误差0.3°，摄像机方位角和高低角误差均为0.02°，激光测距误差5m，设以上误差均服从均值为零的正态分布。进行1000次Monte-Carlo仿真，计算目标的运动速度并统计速度误差。测速误差的统计结果如图5所示。可以看出目标天向、东向、北向的速度误差分布都近似服从μ=0的正态分布，天向速度误差10.5m/s，东向速度误差5.6m/s，北向速度误差10.2m/s。

图5 测速误差的统计图Fig.5 Statistical chart of velocity measurement error

为了描述测速误差和速度真实值的关系，引入相对速度误差概念：Δe=误差/真实值。在上述仿真实验中，天向速度相对误差为10.5/0.5=21，东向速度相对误差为5.6/12=0.47，北向速度相对误差为10.2/12=0.85，真实值几乎淹没在误差中，在这种情况下，算法实用价值不高。因此，有必要探讨测速算法的使用条件，以达到提高测速精度的目的。

在其他仿真条件不变的情况下，增加B时刻目标位置到A时刻目标位置基线距离。设定基线距离由20m增加至170m，基线距离与速度误差的关系如图6所示。从图中可以看出，随着基线距离的增加，天向、东向、北向三个方向的速度误差呈减小趋势，且减小趋势为先快后缓。

产生这种现象的原因是由于各种测量误差的存在，如载机姿态角误差、摄像机指向角误差等，导致对目标的定位有一个半径为R的球形定位模糊区，如图7所示。如果两次定位时目标位置靠近，基线距离较短（如图7（a）），容易导致定位模糊区重合，从而使测速误差增大。增加基线距离，可以有效地解耦定位模糊区（如图7（b）），达到提高测速精度的目的。在实际应用中，增加基线距离意味着增加目标的运动速度，因此该测速算法对于运动速度快的目标有较好的测速精度。

6 结束语

利用航空光电侦察平台进行目标测速是一种新型测速方式。本文推导出一种测速算法，根据载机的自身位置和姿态角、摄像机的方位角和高低角、载机与目标的距离，计算出某时间段内运动目标的起点和终点位置，并将位置信息统一到参考坐标系中，结合时间间隔，求取目标的东向、北向、天向速度。实验结果表明，该算法能够有效测量目标速度，且对运动速度快的目标有较好的测速精度。

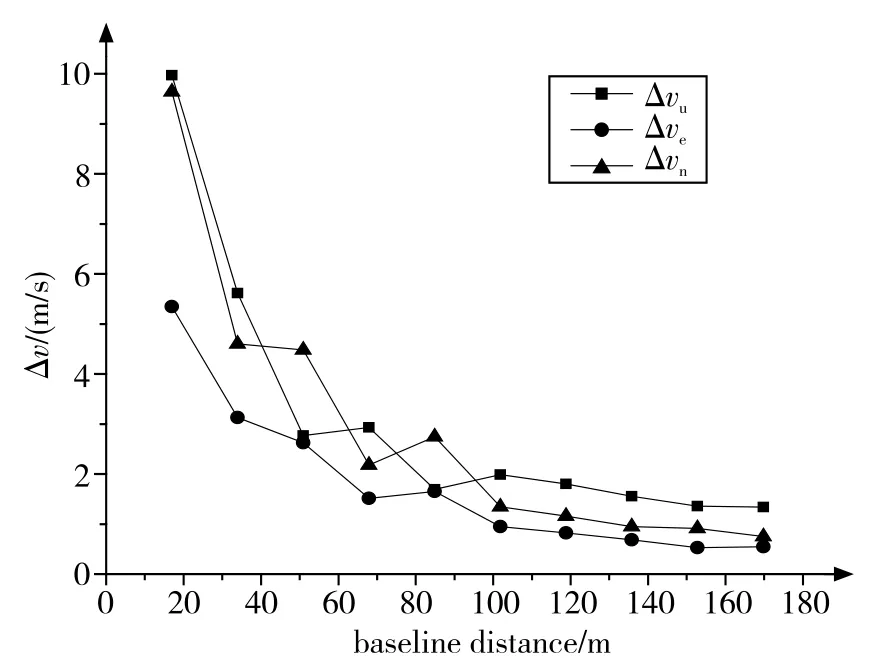
图6 基线距离对测速误差的影响Fig.6 Influence of baseline distance on velocity measurement error

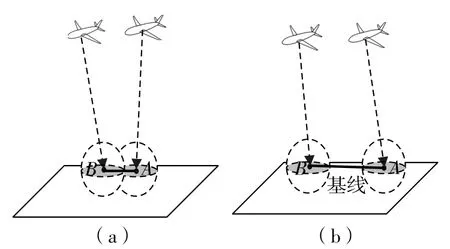
图7 定位模糊区Fig.7 Confusion region of localization

[1]Tisdale J，Ryan A，Kim Z，et al.A Multiple UAV System for Vision-based Search and Localization[C]//American Control Conference.Washington：IEEE，2008：1985～1990.

[2]Quigley M，Goodrich M A，Griffiths S，et al.Target Acquisition，Localization，and Surveillance Using a Fixed-wing Mini-UAV and Gimbaled Camera[C]//IEEE International Conference on Robotics and Automation.Barcelona：IEEE，2005：2600～2605.

[3]毛昭军，汪德虎.姿态测量/激光测距的无人机目标定位模型[J].火力与指挥控制，2003，28（5）：14～17.Mao Shaojun，Wang Dehu.A Model of Target Position for UAV Based Attitude Measuring/Laser Range-finder[J].Fire Control&Command Control，2003，28（5）：14～17.

[4]吴卫玲，宋喜报.多普勒测速雷达测速误差分析[J].计量与测试技术，2000，27（1）：31～32.Wu Weiling，Song Xibao.Error Analysis of Speed Measurement by Doppler Radar[J].Metrology and Measurement Technique，2000，27（1）：31～32.

[5]孙明超，刘晶红，张 葆.高帧频图像融合光学测量吊舱的设计[J].光学精密工程，2013，21（1）：94～100.Sun Mingchao，Liu Jinghong，Zhang Bao.Design of Measuring Gondola System with High Frame Rate for Image Fusion[J].Optics and Precision Engineering，2013，21（1）：94～100.

[6]Rafi F，Khan S，Shafiq K，et al.Autonomous Target Following by Unmanned Aerial Vehicles[C]//Defense and Security Symposium.Orlando：International Society for Optics and Photonics，2006：623010-623010-8.

[7]黄 波.基于机载光电测量系统的图像目标定位技术研究[D].南京：南京航空航天大学，2011.Huang Bo.Research on Image Positioning Technology Based on Airborne Photoelectric Measuring System[D].Nanjing：Nanjing University of Aeronautics&Astronautics，2011.