一种新的无人机运动目标测速技术*
2015-04-25黄大庆周春祎王东振
徐 诚,黄大庆,周春祎,韩 伟,王东振
(1南京航空航天大学无人机研究院 南京 210016 2南京航空航天大学电子信息工程学院 南京 210016)
引 言
现代战争,把握战场态势的发展和瞬时变化的情报信息是获取战场主动权的关键环节。因此,有效获取战场信息的方式和手段就显得尤为重要。目前,常见的侦察手段有电子侦察飞机(有人的)、无人侦察飞机、飞艇、气球等飞行器以及侦察卫星。无人机由于具有体积小、机动灵活、不易被发现等优点,可以在敌占区上空进行长时间低空侦察。同时无人机可以携带多种传感器,能提供多种形式的目标图像和位置信息[1,2]。
无人机光学目标测速是指利用光电侦察平台,结合飞机自身的飞行参数,对运动目标进行测速。这是一种新型的测速方式,具有使用局限性小、便于安装部署的特点。本文深入研究了目标测速的机理,充分利用各种传感器测量数据,建立了包括飞机速度、飞机姿态角速率、摄像机指向角速率等15个变量的测速数学模型,并分析了测速误差的形成原因,推导了误差计算公式,为实现无人机目标测速提供了一条新思路。
1 测速系统介绍
本文讨论的无人机目标测速系统需要装备光电侦察平台、惯导设备以及卫星接收机。光电侦察平台具有稳定跟踪功能:载体的位置和姿态变化会造成光学设备的光轴指向不稳定。光电侦察平台的稳定跟踪要能隔离载体姿态运动和其他干扰力矩所造成的光轴在惯性空间内的抖动,以保证获取清晰的图像;同时根据图像跟踪器输出的信号,形成稳定跟踪控制回路,隔离相对运动干扰,保持目标处于视场中心,实现目标精确跟踪。光电跟踪伺服控制系统是一个包括光电探测、信号处理、控制系统等几部分的复杂设备[3]。它的主要功能是根据传感器送来的目标位置偏差信号的大小及方向控制伺服电机,减小偏差,实现对目标的光电闭环自动跟踪。光电侦察平台结构如图1所示,主要包括:激光测距机、CCD摄像机、红外热像仪、俯仰测角元件、方位测角元件等。
为了推导测速算法,定义如下坐标系[4]:
(1)地理坐标系
在地理坐标系中,原点是载机中心在某一时刻所处的位置,Zn指向正北方向,Xn垂直于地表指向天空,Yn与Zn、Xn相互垂直构成一个右手系,如图2所示。地理坐标系中每一个点的坐标可以表示为(xn,yn,zn)。
(2)载机坐标系
载机坐标系的原点为载机导航系统的中心,Yb代表载机横轴,Zb代表载机纵轴,Xb由载机腹部指向背部。φ为载机航向角,γ为载机俯仰角,θ为载机横滚角,代表该坐标系相对地理坐标系的三轴姿态角。当姿态角均为零时,载机坐标系的三轴指向与地理坐标系的三轴指向重合。在载机坐标系中任一点的坐标表示为(xb,yb,zb)。
(3)摄像机坐标系
摄像机坐标系的原点在摄像机光轴与横轴的交点上,Zc轴为摄像机光轴,指向目标。光轴指向角用方位角α、高低角β表示,其中方位角α为绕方位轴Xc的旋转角度,高低角β为绕俯仰轴Yc的旋转角度。

图1 光电侦察平台结构Fig.1 The structure of electro-optical platform
2 目标测速原理
如图2所示,无人机分别在Pi、Pi+1点对运动目标进行观测,在ti时刻,目标位置在Mi点,在ti+1时刻,目标运动到Mi+1点。为了便于描述,以Mi点的地理坐标系Mi-XYZ作为参考坐标系,其中,X指向天顶,Y指向正东,Z指向正北。Pi-XnYnZn、Pi+1-XnYnZn分别为Pi、Pi+1点的地理坐标系,则坐标系Mi-XYZ、Pi-XnYnZn、Pi+1-XnYnZn的坐标轴相互平行。令在Δt=ti+1-ti时间间隔内飞机平均速度的三轴分量分别为vpx、vpy、vpz,目标运动的平均速度的三轴分量分别为vu、ve、vn,Pi在参考坐标系中的坐标为(xpi,ypi,zpi),Pi+1在参考坐标系中的坐标为(xpi+1,ypi+1,zpi+1),Mi在参考坐标系中的坐标为(xmi,ymi,zmi)=(0,0,0),Mi+1在参考坐标系中的坐标为(xmi+1,ymi+1,zmi+1),则有:
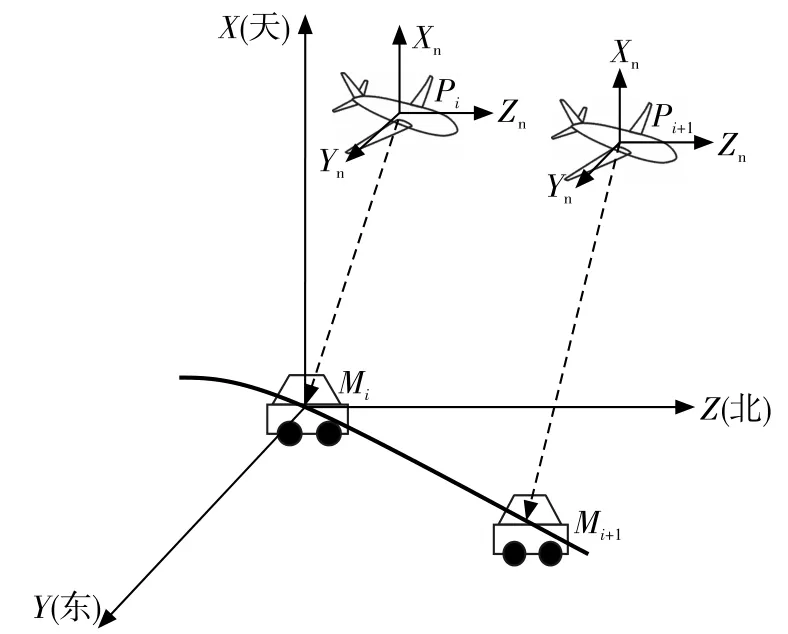
图2 目标测速示意图Fig.2 Schematic diagram of velocity measurement

令Mi在坐标系Pi-XnYnZn下的坐标为(xnmi,ynmi,znmi),Mi+1在坐标系Pi+1-XnYnZn下的坐标为(xnmi+1,ynmi+1,znmi+1),则有:

结合式(1)、式(2),可以推导出在Δt=ti+1-ti时间间隔内目标运动的平均速度:
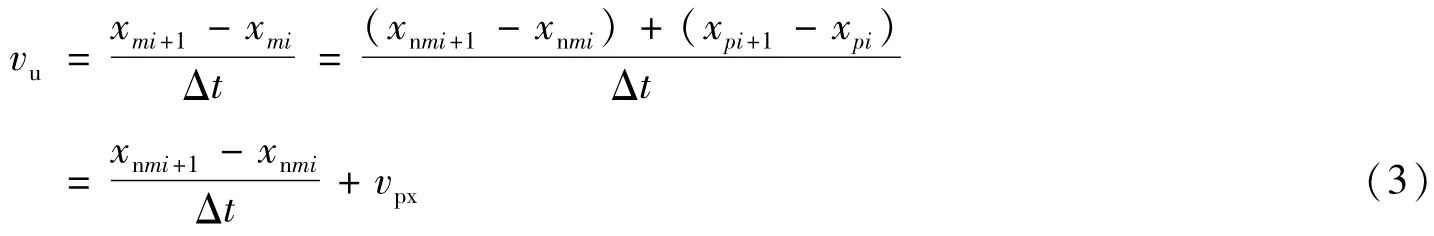
同理有:

以天向速度vu为例,已知:
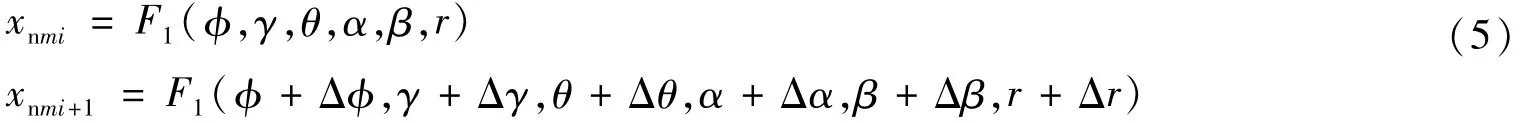
其中,(φ,γ,θ)、(α,β)、r分别为ti时刻的载机姿态角、摄像机方位角和高低角、激光测距值。Δφ、Δγ、Δθ、Δα、Δβ、Δr为ti+1时刻相对ti时刻各个测量值的变化值,F1为目标坐标从摄像机坐标系到地理坐标系的转换过程。将xnmi+1在φ、γ、θ、α、β、r处做一阶泰勒展开有:

其中,o(ρ)为大于2阶的高阶项,且有,当Δφ、Δγ、Δθ、Δα、Δβ、Δr为趋于0的小值时,高阶项可以忽略,根据式(3)、式 (5)和式(6)有:
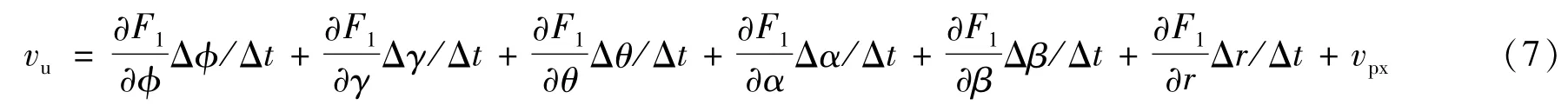
ve、vn求解同vu:
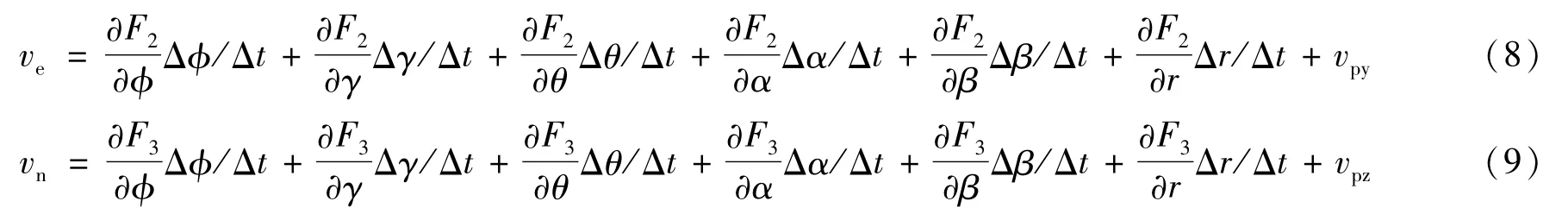
至此,已经推导出Δt时间间隔内目标运动的速度。目标运动速度与当前时刻载机的航向角φ、俯仰角γ、横滚角θ,摄像机的方位角α和高低角β,激光测距值r,载机的航向角速率Δφ/Δt、俯仰角速率Δγ/Δt、横滚角速率Δθ/Δt,摄像机的方位角速率Δα/Δt和高低角速率Δβ/Δt,激光测距值化速率Δr/Δt以及载机的飞行速度vpx、vpy、vpz这15个变量有关。为了便于描述,将载机的航向角速率Δφ/Δt定义为ωφ,俯仰角速率Δγ/Δt定义为ωγ,横滚角速率Δθ/Δt定义为ωθ,摄像机的方位角速率Δα/Δt定义为ωα,高低角速率Δβ/Δt定义为ωβ,激光测距值变化速率Δr/Δt定义为ωr。
目标在载机地理坐标系下的坐标可以通过坐标转换求解得出,如式(10)所示,式中,s(.)为sin(.)的简写,c(.)为cos(.)的简写。将式(10)展开后,得到式(11)。
结合式(7)~式(9)和式(11),求得目标运动天、东、北向的速度表达式如式(12)~式(14)。

式(12)~式(14)中,载机的航向角速率ωφ、俯仰角速率ωγ、横滚角速率ωθ可由机载惯导系统获得,摄像机的方位角速率ωα和高低角速率ωβ由光电侦察平台中的角速度传感器测量获得,激光测距值变化速率ωr可以由两次激光测距值结合测量间隔时间求得。在实际使用中,以上各个速率的测量应在相同的时间周期内进行,确保时间同步。
3 误差分析
通过前面的推导,可知造成目标测速误差的来源有:载机姿态角误差(Δφ、Δγ、Δθ)、载机姿态角速率误差(Δωφ、Δωγ、Δωθ)、摄像机指向角误差(Δα、Δβ)、摄像机指向角速率误差(Δωα、Δωβ)、激光测距误差Δr、激光测距变化速率误差Δωr以及载机的飞行速度误差(Δvpx、Δvpy、Δvpz)。使用全微分法求解目标测速误差,以运动目标在天向的速度分量误差Δvu求解为例,分别对各个变量求偏导,得到式(15)。
结合式(12)即可求得具体的天向速度误差表达式,如式(16)。Δve、Δvn求解方法同Δvu。

4 实验结果及分析
为了验证上述方法的正确性与可行性,用仿真数据对其进行了考核。首先以接近实际条件设定目标和测控飞机的运动规律,生成一组目标空间位置坐标和飞机位置坐标,并计算出对应的飞机与目标连线夹角(即摄像机视轴指向角)理论值,考虑到实际情况下各测量参数都会存在误差,还需要对这些参量加入不同的噪声,然后根据本文方法解算出运动目标在不同时段的平均速度,与仿真条件设定的运动目标速度进行比对,验证方法的正确性并统计其精度。
仿真条件设定为:

其中,(
x
p
,
y
p
,
z
p
)为飞机运动轨迹,(
x
m
,
y
m
,
z
m
)为目标运动轨迹。根据工程经验,设定各测量参数误差均服从零均值高斯分布,具体为:飞机姿态角(航向角、俯仰角、横滚角)误差为0.3°,姿态角速率误差为0.08°/s;摄像机指向角(方位角、高低角)误差为0.03°,指向角速率误差为0.01°/s;激光测距误差为5m,测距变化速率误差为5m/s;飞机速度误差为5m/s。
设定每隔1s进行一次测速,获取90组测速值,并对每组测速值进行1000次仿真计算,统计最终的目标测量速度。图3给出了历时90s,目标点的测量速度与实际速度的分布。图中,速度输出为天向、东向、北向三个分速度的合成,可以看出,运动目标的测量速度与实际速度基本吻合,证明本文的目标测速算法可以有效地测量运动目标速度。
造成目标测速误差的来源有:载机姿态角误差(Δφ、Δγ、Δθ)、载机姿态角速率误差(Δωφ、Δωγ、Δωθ)、摄像机指向角误差(Δα、Δβ)、摄像机指向角速率误差(Δωα、Δωβ)、激光测距误差Δr、激光测距变化速率误差Δωr等,为了得到各测量误差对目标测速误差的影响曲线,设定其他误差均为0,改变其中某一误差的值,考察其对测速误差的影响,所得结果如图4和图5所示。
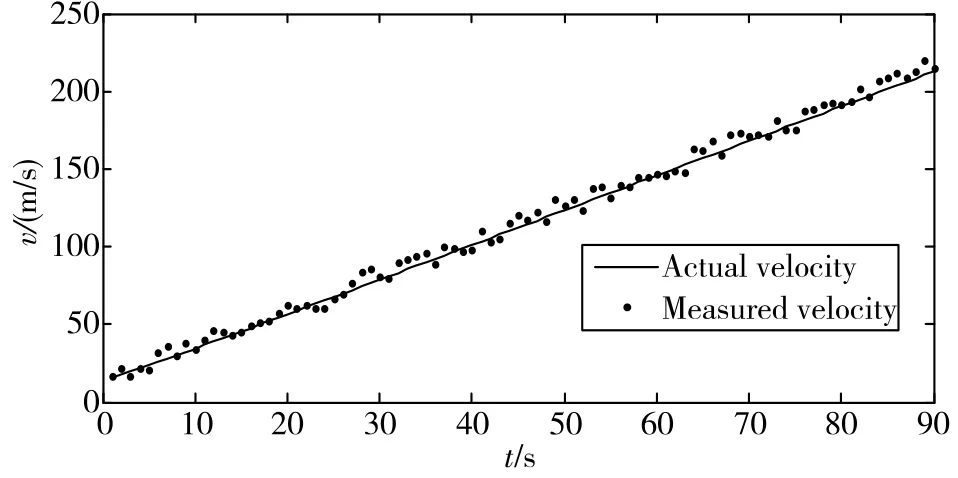
图3 仿真实验结果Fig.3 The simulation result
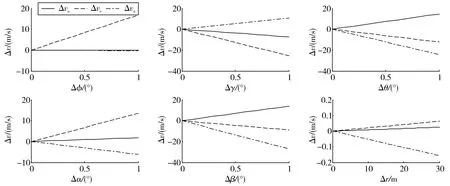
图4 测量参数误差对测速精度的影响Fig.4 Influence of parameter error on velocity measurement precision
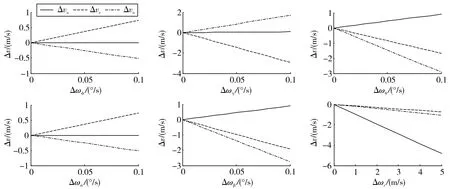
图5 测量参数变化速率误差对测速精度的影响Fig.5 Influence of parameter variation rate error on velocity measurement precision
实验结果表明,载机俯仰角误差、横滚角误差、摄像机高低角误差对测速精度有明显影响,载机航向角误差和摄像机方位角误差对测速精度影响相对较小,激光测距误差对测速精度影响很小,可忽略不计;载机俯仰角速率误差、横滚角速率误差、摄像机高低角速率误差对测速精度的影响比载机航向角速率误差和摄像机方位角速率误差对测速精度的影响明显,激光测距变化速率误差对东向和北向的测速精度影响很小,而天向测速误差和激光测距变化速率误差近似相等。
5 结束语
本文研究无人机对运动目标的光学测速技术,建立了包括飞机速度、飞机姿态角速率、摄像机指向角速率等15个变量的测速数学模型,并分析了测速误差的形成原因,推导了误差计算公式。实验结果表明,在无人机上利用光电侦察平台和无人机导航数据对运动目标进行测速是可行、有效的,为无人机对地目标测速提供了一条新思路。
[1]李德仁,李 明.无人机遥感系统的研究进展与应用前景[J].武汉大学学报信息科学版,2014,39(5):505~513.Li Deren,Li Ming.Research Advance and Application Prospect of Unmanned Aerial Vehicle Remote Sensing System[J].Geomatics and Information Science of Wuhan University,2014,39(5):505~513.
[2]沈 东,魏瑞轩,茹常剑.基于数字信息素的无人机集群搜索控制方法[J].系统工程与电子技术,2013,35(3):591~596.Shen Dong,Wei Ruixuan,Ru Changjian.Digital-pheromone-based Control Method for UAV Swarm Search[J].Systems Engineering and Electronics,2013,35(3):591~596.
[3]王家骐,金 光,颜昌翔.机载光电跟踪测量设备的目标定位误差分析[J].光学精密工程,2005,13(2):106~112.Wang Jiaqi,Jin Guang,Yan Changxiang.Orientation Error Analysis of Airborne Opto-electric Tracking and Measuring Device[J].Optics and Precision Engineering,2005,13(2):106~112.
[4]徐 诚,黄大庆.无人机光电侦测平台目标定位误差分析[J].仪器仪表学报,2013,34(10):2265~2270.Xu Cheng,Huang Daqing.Error Analysis for Target Localization with Unmanned Aerial Vehicle Electro-optical Detection Platform[J].Chinese Journal of Scientific Instrument,2013,34(10):2265~2270.
