化学发光免疫分析仪机械臂设计与有限元分析

袁振清，杨东超，王 峤

YUAN Zhen-qing, YANG Dong-chao, WANG Qiao

（清华大学 机械工程系，北京 100084）

0 引言

现如今食品质量安全问题已经得到了社会各方的广泛关注。当食品质量受到化学毒素残留或微生物污染时，人们的生命健康会受到危害。本课题涉及的“全自动化学发光免疫分析仪”是用于食品安全检测的仪器设备，其主要功能是利用化学发光免疫分析法对特定样品进行化学分析，检验其中特定物质的浓度[1]。该分析法主要包含两个部分：免疫化学反应和化学发光反应[2]。免疫化学反应是用化学发光相关物质标记到抗原或抗体上，与待测物（抗体或抗原）进行特异性反应，结合形成抗原抗体免疫复合物。化学发光反应是在免疫化学反应完成后，加入发光底物，化学发光物质经过反应后处于激发态，此时发射光子释放能量回到基态。由于发光强度与待测物质的浓度成一定的关系，因此可利用仪器检测光信号，进而获得待测物质的浓度。

化学发光免疫分析仪在欧美研制较早，技术比较成熟的产品有瑞士的罗氏（Roche）、美国的雅培（Abbott）、英国的朗道（Randox）、德国的拜耳（Bayer）。中国起步较晚，但因其市场需求增加以及政策扶持，我国同欧美国家技术差距正在逐步缩小。目前国内化学发光免疫分析仪主要来源进口，而欧美国家的产品价格昂贵，使用维护费用高，因而研发具有我国自主知识产权的化学发光免疫分析仪具有重要的科学和工程意义。

基于上述分析，本文完成了化学发光免疫分析仪转盘平台和机械臂的详细设计，并通过建立机械臂精确的有限元模型和接触设置，实现机械臂装配体的精确的有限元分析，验证校核了机械臂设计，进而完成机械臂零件的加工和装配。

1 化学发光免疫分析仪总体设计

如图1所示，化学发光免疫分析仪功能结构主要由两部分组成：自动进样模块和微光检测模块。

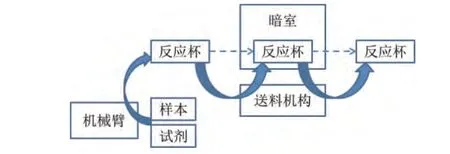
图1 化学发光免疫分析仪功能结构

自动进样模块主要由机械臂和送料机构组成，机械臂负责样本与试剂的添加以及反应杯的夹持与释放，送料机构负责控制反应杯进出暗室。微光检测模块由测量暗室、光纤和光电倍增管等部分组成，化学发光反应以及发光值的测量在暗室中进行。

依据图1所示的功能结构，化学发光免疫分析仪整体结构方案设计如图2所示：整机结构由2个机械臂、3个转盘和1个暗室组成。存储盘用于存储反应杯、试剂与样品，以供应作业盘的连续作业；机械臂2负责将作业盘内圈的试剂与样品加入到反应盘上的反应杯；反应盘转动控制反应杯进出暗室发生化学发光反应；机械臂1负责将作业盘外圈的反应杯送到反应盘并将从暗室出来的已完成化学发光反应的反应杯送到回收处。采用伺服电机协调控制3个转盘的转动与2个机械臂的路径和起停实现整机的连续作业。

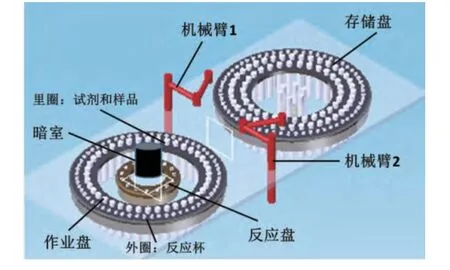
图2 第二代样机整体结构方案设计

方案采取两机械臂对称布置，机械臂1用于运送反应杯从作业盘到反应盘再到回收处，要求机械臂具有反应杯的加持与释放功能；机械臂2将作业盘上的样品与试剂添加到反应盘上指定反应杯中。两机械臂具有同样的作业特点，都要求定位精度高，占用空间小，工作空间大同时具有正拟运动学解算功能。机械臂的设计工作是本课题的难点，由于两机械臂对称布置且结构功能相似，因而可统一设计。因此本文将详细讲解机械臂1的设计与装配体有限元分析工作。

2 机械臂总体结构设计

根据机械臂的作业要求，机械臂在水平面上应至少具有两个转动关节，实现末端在水平面内任意一点的定位，同时须有升降动作实现反应杯的加持与释放。以机械臂1为例，其作业流程是：机械臂下降到反应杯位置停止，夹持反应杯，上升一定距离停止（避免运送过程跟其他反应杯试剂等干涉），运送反应杯到反应盘上方停止，下降并将反应杯释放到反应盘，当反应杯从暗室转出，机械臂下降夹持反应杯，上升并将其运送到回收处释放。

满足上述机械臂作业要求的现有机器人是Scara机器人。Scara机器人因广泛用于零件的搬取和装配而闻名，通常前两个转动关节实现末端定位，末端的旋转和升降关节实现零件的搬取和装配。而国内外的Scara机器人通常末端机构繁重复杂，对零件机械刚度以及加工装配等都有很高的要求。本课题涉及的反应杯质量轻（5g）、体积小，不需要Scara机器人复杂繁重的末端设计，对电机的功率尺寸要求也较小，又具有急停和正反转应用场合，因而自主设计一种具有快速反应，结构简单轻巧，运转稳定的机械臂具有重要意义。

大的自重会降低系统的固有频率，使系统响应速度变差，抗干扰能力减弱，本设计本着减小自重的原则，材料选用铝合金。图3为转盘平台与机械臂1在SolidWorks中的三维模型图。

如图3所示，机械臂由直线导轨导引机构、大臂肩关节机构、小臂肘关节机构、末端执行机构组成。直线导轨固定在基座上，机械臂肩关节固定在直线导轨的螺母上，大臂和小臂能在螺母的带动下竖直升降运动。肩关节和肘关节是转动关节，实现末端在水平操作空间内任意一点的定位，移动关节实现大臂和小臂整体的垂直升降动作，确保末端机构在运转过程中不与反应杯试管发生干涉碰撞。末端机构采用电磁铁驱动镊子张合实现反应杯的拾取和释放。

图3 机械臂1的装配体三维模型

相对于Scara机器人，本设计把升降关节设计在机械臂的起始端，简化缩小了末端结构，降低了零件刚度以及对加工装配的要求，避免了Scara机器人因刚度低以及装配精度不够带来的颤振现象，同时对材料的选取以及结构的优化带来了很大的便捷。同时关节尺寸轻巧，整体转动惯量小，快速反应性能好，定位精度高。下文将展开机械臂各模块的详细设计。

2.1 直线导轨导引机构

如图4所示，基座固定在转盘平台上，直线导轨固定在基座上，下端用托盘和法兰定位，法兰用于连接减速器和电机。肩关节基座固定在直线导轨螺母上，带动大臂和小臂随螺母上下移动，采用Maxon RE30伺服电机和GP32A行星减速器驱动直线导轨。滚珠丝杠直线导轨精度高、承载能力大、运动快速，较好地满足机械臂升降关节的要求。

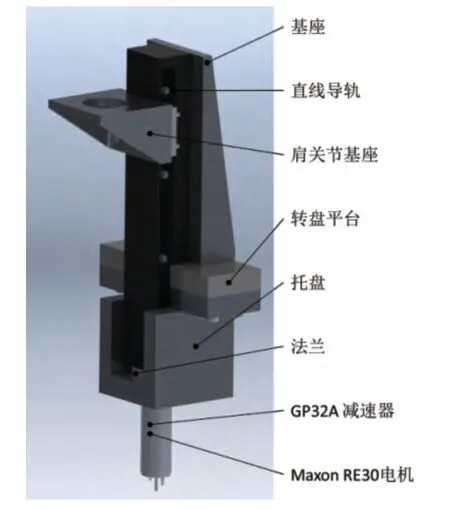
图4 直线导轨导引机构

2.2 大臂肩关节机构

如图5所示，整个大臂肩关节固定在肩关节基座上，电机与减速器通过法兰固定在轴承座上，轴承采用7001AC角接触球轴承，背靠背装配增加轴向刚度，通过轴孔和轴承盖以及轴用弹性挡圈实现轴承双向固定，采用垫圈施加预紧。关节轴通过紧定螺钉与减速器轴实现同步转动，轴承座留有工艺孔用于紧定螺钉的拧紧。关节轴顶端穿透大臂实现自身定位且增加轴向装配刚度，大臂通过长螺钉与关节轴固结。肩关节采用Maxon RE25直流伺服电机和GP 26A行星减速器。

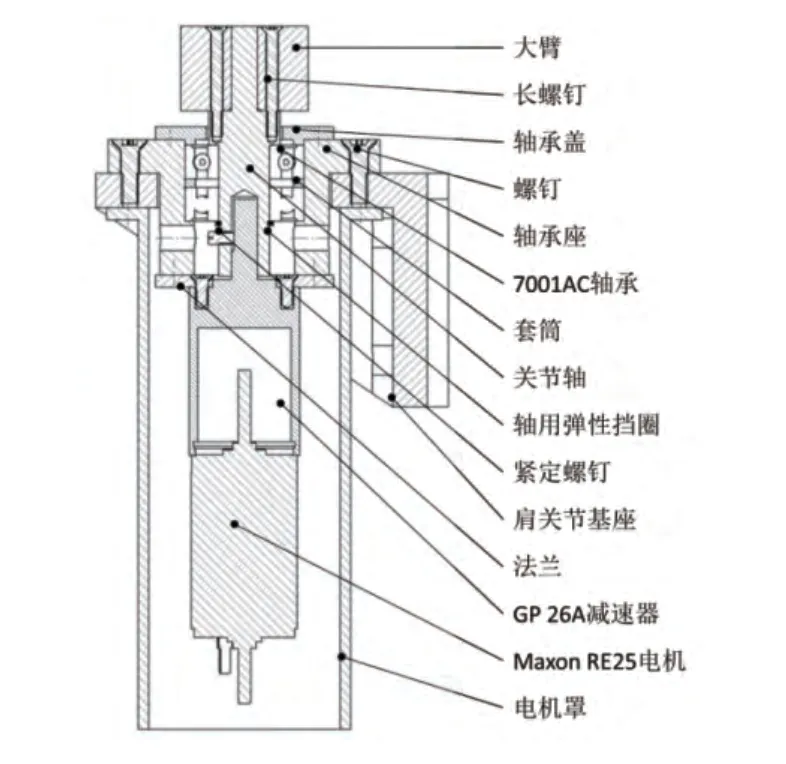
图5 大臂肩关节机构

2.3 小臂肘关节机构

如图6所示，电机与减速器通过法兰固定在大臂上，轴承采用S719/8角接触球轴承，背靠背装配，两端固定，通过垫圈施加预紧。关节2轴上端通过紧定螺钉与减速器轴同步转动，下端插入小臂增强轴向刚度，通过自身与小臂定位并采用紧定螺钉张紧，通过轴端挡圈与小臂固结。电机和减速器安装在大臂上面，避免其在升降过程中与反应杯、试管等发生干涉碰撞，减小机械臂对操作空间的要求。相对于Scara机器人将电机固定在小臂上，本设计将电机与减速器固定在大臂上，从而减小小臂转动惯量，减小轴承的轴向承载能力，进而简化关节尺寸。小臂肘关节采用Maxon RE-max17直流伺服电机，GP 16A行星轮减速箱。

2.4 末端执行机构

图7 末端执行机构

如图7所示，末端采用电磁铁控制镊子张合实现反应杯的夹持与释放。电磁铁未通电时，镊子末端保持闭合状态，镊子伸进反应杯内，电磁铁通电，电磁吸力迫使镊子上端闭合下端张开，从而张紧反应杯内壁，实现反应杯夹持动作；驱动反应杯到达指定地点，电磁铁断电，磁力消失，镊子在自身弹性作用下恢复闭合状态，实现反应杯的释放动作。本设计轻巧便捷，相对一般末端手抓机构，大大简化了装配和控制工作。同时采用内部张紧代替外部夹取，镊子在反应杯内部具有自我调心功能，降低了机械臂末端定位精度的要求。内部张紧还避免了外部夹持时手抓与其他反应杯干涉碰撞的可能。

3 装配体有限元模型分析验证

很多时候有限元分析只针对单一零件，装配体也经常被视为一个整体的零件去分析，不能模拟装配体不同零件之间真实的接触关系以及力的传递。准确的装配体有限元分析将直观地反映整机的刚度和稳定性能，快速凸显整机当中的薄弱环节。本文将建立装配体精确的有限元模型，通过准确的接触设置，模拟不同零件之间的接触关系以及力的传递，实现机械臂的静力学分析和模态分析。机械系统的静力学性能和模态性能至关重要，静态刚度太小会降低系统的固有频率，导致响应速度变慢，抗干扰能力变差，容易出现过冲现象影响控制精度[4]。模态分析用于确定结构或机器部件的振动特性，对实际机电控制具有重要意义，同时模态分析还是其他动力学分析的基础。

3.1 装配体有限元模型的建立

装配体的倒园倒角以及螺钉螺纹等不规则形状会使有限元中网格划分以及应力应变求解变得异常复杂，而对计算结果没有太大影响，有时复杂的细节会导致计算停滞甚至使求解更不精确。重新建立装配体有限元模型，去除倒园倒角等特征，去除电机，把电机重量和驱动转矩通过边界条件施加在相应在关节上。因末端镊子、电磁铁的静态刚度和模态主要取决于整机的刚度和模态，因而去除末端镊子、电磁铁，把其重量通过边界条件施加到小臂末端。

对装配体螺钉螺纹孔作如下处理：去除连接两个面用于承载法向拉力或压力的螺钉螺纹孔，对这两个面采取粘接接触（承载法向拉压力的螺钉螺纹就是用于固结两个面，现已有粘接接触，螺钉螺纹可去除）；连接两个面用于承载剪切力的螺钉和螺纹孔采用同样大小的圆柱体和圆柱孔代替（同样大小的圆柱体不会导致承载剪切力的变化，圆柱体的替代可模拟力的传递，释放计算资源）；起始端连接转盘平台用于固定机械臂的螺纹孔改用同样大小的圆柱孔（用于设置边界条件模拟机械臂受到的实际约束，有限元分析的准确与否首先取决于有限元模型建立是否准确，其次取决于边界条件的设置是否准确）。

关节轴系结构对机构的静态刚度和模态分析有很大影响，因而关节轴系结构的有限元模型应最大限度地逼近实际情况。因角接触球轴承中的滚珠和沟槽等会使应力应变的计算异常复杂，为模拟轴承的实际工作情况并简化计算，现对两个转动关节的角接触球轴承作如图8所示模型转换。

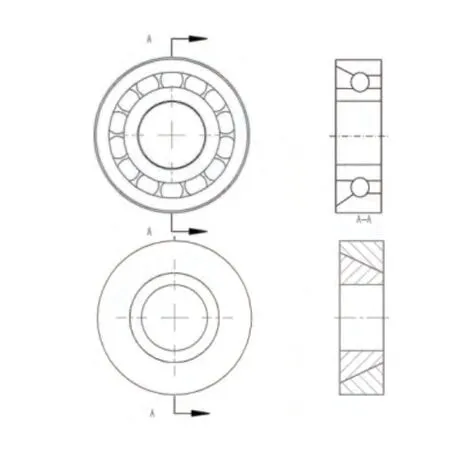
图8 角接触球轴承有限元模型

3.2 装配体接触设置

接触设置是区分单一零件的有限元分析和装配体有限元分析的依据。正确的接触设置能准确地模拟不同零件之间力的传递，ANSYS Workbench设置了五种接触：粘接（Bonded）、不分离（No Separation）、无摩擦（Frictionless）、粗糙的（Rough）和有摩擦（Frictional）。不同接触的使用方法可以参阅相关书籍和文献。

现对装配体作如下接触设置：对采用螺纹连接或胶水粘接等不可能有相对移动的表面之间采取粘接（Bonded）接触；对不分离且有相对滑动的可能的平面之间采取不分离（No Separation）接触，比如轴承内圈和轴以及轴承外圈和孔因受热膨胀可能会有小的轴向游动；对相对滑动的表面之间采取有摩擦（Frictional）接触，比如简化后角接触球轴承的内外圈之间。

此机械臂装配体系统中，轴承内外圈与轴孔之间以及轴承盖与轴承外圈之间的接触采用不分离（No Separation）接触；轴承内外圈之间采用有摩擦（Frictional）接触，摩擦系数设为角接触球轴承内外圈之间的滚动摩擦系数，滚动轴承内外圈之间摩擦系数一般为0.002～0.003之间[5]，本实验选为0.003；其余有螺纹连接的两平面之间采用粘接（Bonded）接触。

为了计算准确，确保接触面和目标面不能相互渗透，选择对称接触行为（Symmetric）。Workbench Mechanical 共有四种接触公式在接触界面强制协调。它们分别是：增强拉格朗日（Augmented Lagrange）、罚函数法（Pure Penalty）、多点约束法（MPC）和拉格朗日（Lagrange）。前两者使用积分点探测，具有较多探测点。后两者采用节点探测，具有较少探测点。Normal Lagrange和MPC要求非对称行为，对称行为只能用Augmented Lagrange和Pure Penalty公式。

Pure Penalty和Augmented Lagrange的区别是后者加大了接触压力的计算，罚函数和增强拉格朗日的表达式分别如式(1)和式(2)所示：

因额外因子λ，增强拉格朗日对于罚函数法向刚度knormal的值变得不敏感，因而自动减小渗透，但伴随着消耗更多计算的代价。小的穿透量会使计算更精确，但也使求解更慢，更不容易收敛。以拉格朗日和罚函数为例说明这一矛盾。如图9所示，如果不允许渗透（Lagrange），在gap为0处，无法判断接触状态是开放还是闭合（如阶跃函数）。这导致收敛变得困难，因为接触点总是在open/closed中间来回震荡，造成接触扰动（chattering），如果允许微小渗透（Pure Penalty），收敛变得容易，因为接触状态不再是一个阶跃变化。

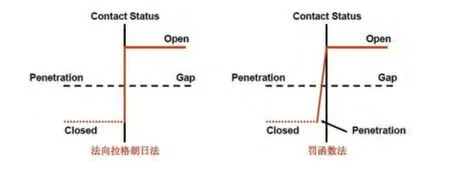
图9 拉格朗日和罚函数收敛容易程度的比较

通过以上分析，对粘接和不分离接触采用Pure Penalty和大法向刚度，罚函数使计算容易收敛，大法向刚度减小渗透量保证计算精度；对有摩擦接触采用Augmented Lagrange。此种对不同接触类型搭配不同接触公式的方法最大化地解决了计算精度和收敛容易之间的矛盾。

3.3 机械臂静力学分析

采用Mechanical自动网格划分，设置边界条件。对固定基座的4个圆柱孔采用固定约束（Fixed Support），对用于垂直定位的直线导轨下端面采用无摩擦约束（Frictionless Support）。当机械臂各臂水平伸直至最长时，机器人承受的力矩载荷最大，此时处于最危险的工作状况，机器人自由端的位移量也最大，因此选择该姿态进行有限元分析[6]。图10显示了机械臂整体位移云图。如图所示，小臂末端最大位移量为Z方向0.035mm，满足机械臂对静态刚度的要求。

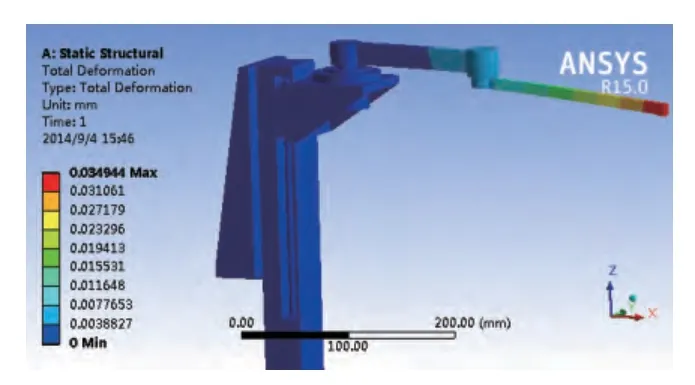
图10 机械臂静力学位移云图

图11 显示了机械臂的应力云图，由上图可知，大臂小臂的应力很小，隐藏大臂，显示轴关节，可以看出转动关节的轴承所受较大的应力，符合机械臂轴系结构的实际承载情况。一般情况下最大许用应力应为材料屈服极限的0.5~0.8，此机械臂最大静态应力为69.5Mpa，远远小于材料的屈服极限。

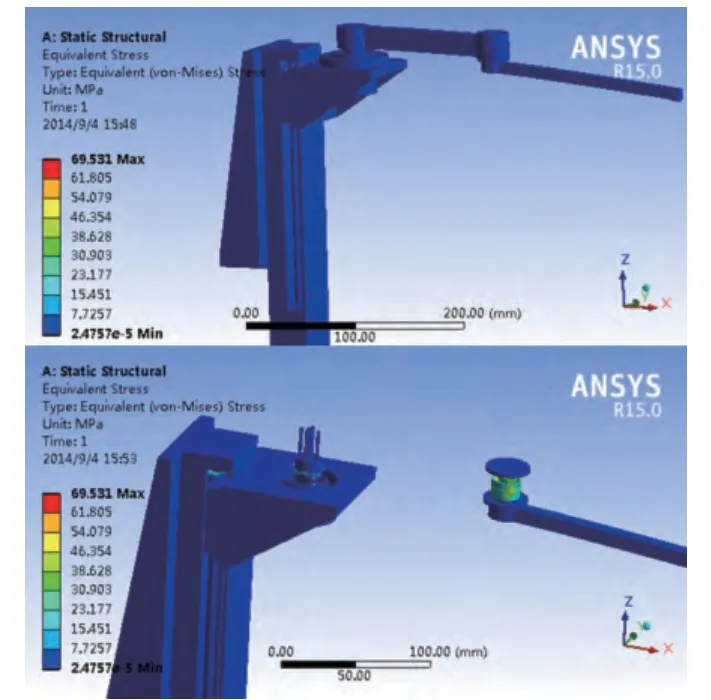
图11 机械臂静力学应力云图

3.4 机械臂模态分析

对机器人进行模态分析可以得出机器人不同阶数的固有频率和振型，指导整机结构的进一步改进。整机的模态与其结构和质量的分布有着密切的关系[7]，而与承载情况无关。即机器人位姿不同则模态也将有所差异。机器人工作状态下位姿是不断变化的，无法求解其全部位姿的模态，因机械臂在大臂小臂伸直至最危险情况下，最容易振动，系统最不稳定，因而模态分析依旧选择最危险的姿态进行分析计算。

本机械臂是具有3自由度的串联机器人，位姿是用3个广义坐标确定的，所以分析前3阶模态就能得出整个机械臂的动态特性[6]。模态分析所需参数设置和静力学分析一样。图12由上而下给出了机器人前3阶的振型图，由于实际形变较小，为直观清晰看出整机的形变，各振型图均进行了形变放大处理。

如图12所示，第1阶振型表现为大臂小臂以肩关节为中心的水平摆动；第2阶振型表现为大臂小臂以肩关节为中心的竖直摆动；第3阶振型表现为大臂小臂绕小臂中心的水平摆动。由各阶振型可知：由于大臂小臂伸直至最危险状态，大臂小臂伸出较长，整个机械臂的水平刚度有待提高。该机械臂的后续结构改进应着重增强大臂小臂的刚度，比如在保证强度的情况下将大臂小臂改为中空结构。

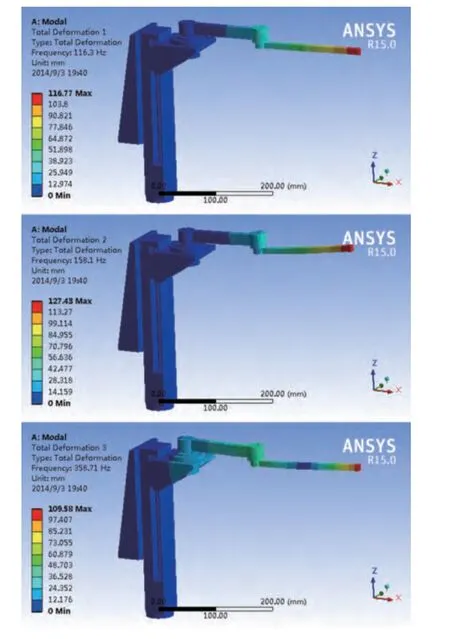
图12 机械臂前3阶振型图

机械臂前3阶固有频率分别为116.3Hz、158.1Hz、358.71Hz，高于一般机器人的前3阶固有频率，固有频率越大说明结构越稳定，为防止机械臂产生共振，外部驱动频率应尽可能避开上述3阶振型对应的固有频率。

通过有限元的静力学分析和模态分析，验证校核了机械臂设计的合理性，因而对转盘平台和机械臂系统进行加工和装配，图13展示了转盘平台和机械臂系统的总体装配图。

图13 机械臂系统总装图

4 结论

本文完成了科技部国家重大科学仪器设备开发专项第二代样机——转盘式化学发光免疫分析仪的总体结构设计，完成了机械臂的详细设计，相对于SCARA机器人，本设计轻巧便捷，降低了系统对零件加工和装配精度的要求，适合机械臂急停和正反向工作的场合。

通过建立装配体精确的有限元模型和接触设置最大化地模拟装配体不同零件之间力的传递，实现有限元静力学和模态的精确分析，进而验证校核机械臂设计的合理性，从而完成了转盘平台和机械臂系统的加工和装配，为后期机械臂路径规划调试创造基础。

[1] Arakawa H, Maeda M, Tsuji A. Enzyme immunoassay of cortisol by chemiluminescence reaction of luminolperoxidase[J]. Bunseki Kagaku,1977,26(5): 322-326.

[2] 邱云青,李凤琴.化学发光免疫分析技术在食品有害因素检测中的应用[J].国外医学(卫生学分册),2009,06:371-374.

[3] 王军锋,唐宏.伺服电机选型的原则和注意事项[J].装备制造技术,2009,11:129-131.

[4] 毛燕,徐晓宇,高峰.SCARA机器人的结构动态设计与改进[J].机械,2007,07:56-58.

[5] 朱爱华,朱成九,张卫华.滚动轴承摩擦力矩的计算分析[J].轴承,2008,07:1-3.

[6] 陈祝权,梁晓合,林粤科,王念峰.六自由度串联机器人结构设计及有限元分析优化[J].机床与液压,2013.12:98-101.

[7] 程丽,刘玉旺,骆海涛.165kg焊接机器人有限元模态分析[J].机械设计与制造,2012,1: 147-149.