非完整单足跳跃机器人姿态运动控制的样条逼近方法

杨莉莉

YANG Li-li

(淄博职业学院，淄博 255314)

0 引言

随着机器人应用领域的不断拓展，作为仿生机器人领域的跳跃机器人，因自身的结构特点从而具有较强的环境适应能力，在实际应用时，能够模拟袋鼠、青蛙等动物的跳跃方式，轻松跃过数倍于自身高度的障碍物或低洼场地、沟渠、坑道，可替代人类用于危急情况下复杂地段的作业，因而在考古、军事、勘探、救援等领域中有广泛应用，此外，对跳跃机器人的研究有助于提高人类对动物奔跑、跳跃运动机理的认识和掌握，对指导跳高跳远等跳跃类运动具有很好的启发意义。同时，跳跃机器人的研究涉及多体系统动力学、非线性动力学、稳定性控制及优化算法等多种学科基础理论和关键技术，近年来一直是机器人研究领域的热点和难点问题。

自1980年美国学者Raibert研制出世界上最早的单足弹跳机器人[1]以来，国内外学者以此机器人模型为基础开展了大量的研究[2]，如对机器人模型的稳定性研究[3]、跳跃运动步态的研究[4]、动力学特性分析[5]以及相关的控制理论研究[6]等。作者[7]考虑机器人系统的非完整约束特性，通过引入遗传算法，研究了单足跳跃机器人非完整运动规划的最优控制问题，得到控制系统运动的最优控制规律，但从仿真实验结果看，利用此方法得到的最优控制输入在系统运动的初始和终止时刻均不为零，不便于利用电机实现对机器人系统运动的控制。

为解决这一问题，本文利用样条逼近方法替代文献[7]中的傅里叶基逼近方法，在实际仿真实验时选用三次样条逼近方法进行拟合，通过粒子群优化算法求得初值和终值均为零的最优控制输入，并在设定的运动周期内控制机器人从初始位姿运动到期望的末端位姿。首先建立系统的动力学模型，在系统角动量守恒的情况下，将带有非完整约束的系统运动规划问题转化成最优控制问题，引入样条逼近方法和粒子群优化算法，得到系统姿态运动的优化运动轨迹和在运动初始及终止时刻系统控制输入均为零的最优控制规律。文末结合算例进行了数值仿真，结果表明所提出的方法对非完整单足跳跃机器人姿态运动控制是有效的。

1 单足跳跃机器人模型

设单足跳跃机器人系统由本体和一条可转动并能伸缩的可驱动腿构成，如图1所示，系统具有二个自由度，可做平面运动。根据多体系统动力学理论，在无外力矩作用时，系统的“约束”为角动量守恒，则有单足跳跃机器人系统的角动量[1]：

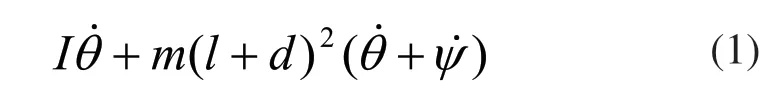
式中，I为机器人本体的惯性矩阵，m为腿的质量，并假定集中在脚上，d 为上腿长度。q=为机器人系统位形参数，其中，为驱动腿相对于本体的转角，l 为腿的伸缩量，为本体的转角。

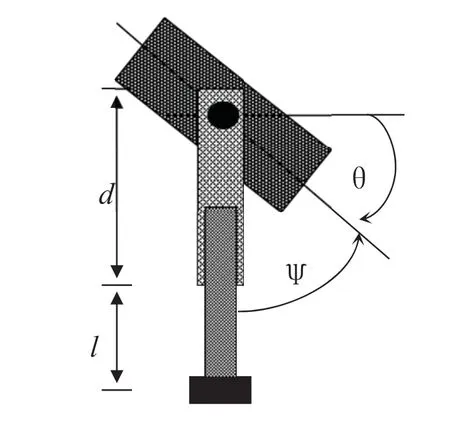
图1 单足跳跃机器人模型

当机器人处于腾空状态时，设系统初始角动量为零，则由式（1）可得：

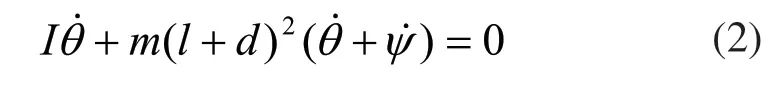
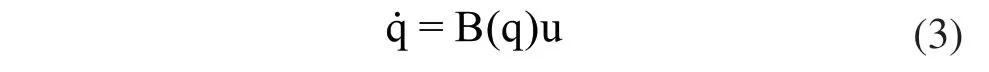
由系统角动量守恒得到的式（3）为不可积的形式，即单足跳跃机器人系统具有不可积的角速度约束，也称为非完整约束[8]。

2 系统姿态运动的优化控制问题

由式（3）可知，q是u和t的函数。式（3）可视为单足跳跃机器人姿态运动（3个状态变量）受控于2个控制输入的控制系统。当给定系统运动的初始位形和末端位形后，通过优化给定的目标函数可以求得一组最优控制输入控制系统在运动周期T内从q0运动到qf。

当系统运动时，其姿态会发生相应的变化，当姿态快速变化时，会消耗较多的能量[9]，因此，可将能耗作为系统运动的优化目标。根据最小能量原理，选择机器人姿态运动时消耗的能量作为最优控制目标，其目标函数可表示为：

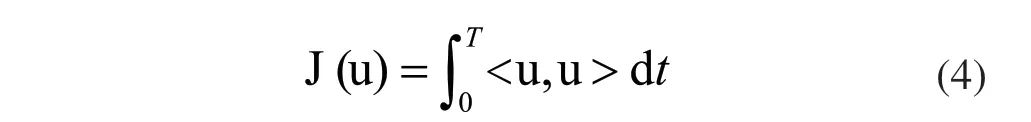
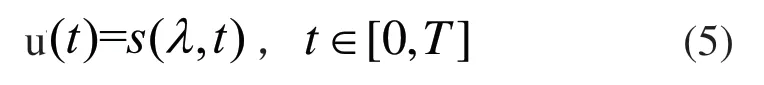
将式（5）代入式（4）中，即可求得系统的目标函数值，将控制输入向量λ视为新的控制变量，考虑系统运动到末端位置的精度约束，引入罚函数法，则式（4）可表示为：

3 系统运动规划的粒子群优化算法

粒子群优化算法[10]（简称PSO），是基于鸟类集群觅食行为而提出的一种模拟群体进化的智能优化算法。在利用该算法时，每个备选解都被视为一只鸟，称为“粒子”。多个“粒子”构成鸟群，在搜索空间内寻优。每个粒子都有一个目标函数值，在搜索时不断优化该值来跟踪当前群体的最优位置，此外，粒子还有一个速度决定它们飞翔的方向和距离。实际计算应用时，每个粒子的初始位置和速度随机产生，通过迭代进化在解空间内搜寻最优解。设每个粒子的维数为D维，第i个粒子的位置矢量为速度矢量

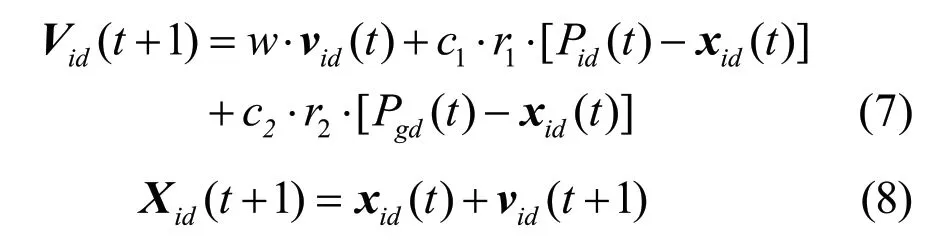
其中w为惯性因子； 1 2,c c 为加速因子，其取值为正常数；之间均匀分布的随机数；粒子的第维的位置和速度变化均有固定取值范围，在迭代时，若粒子的位置和速度超过边界范围则取边界值。

应用于非完整单足跳跃机器人系统姿态运动规划的粒子群优化算法，其计算步骤如下：

2）更新粒子速度和位置。根据式（7）和式（8）更新粒子的速度和位置。

3）判断是否需更新目标函数值。根据式（6）计算每个粒子的目标函数值。如果当前的目标函数值优于更新前的目标函数值，则更新目标函数值。若所得的Pi和Pg值优于更新前的Pi和Pg值，则更新Pi和Pg值。

4） 检验终止条件。若程序达到预先设定的最大迭代次数，则终止程序并输出最优解，否则转到步骤2）继续迭代直到到达最大迭代次数。

4 基于样条逼近的算例仿真

以单足跳跃机器人模型为算例，如图1所示。设定系统的质量几何参数为：

仿真实验时，取T=5s，将[0,T]进行5等份，令控制输入的初值和终值均为零，则每个控制输入对应的参数个数为4，两个控制输入对应的λ的维数为8。取粒子群优化算法的控制参数[11]分别为：粒子个数n=1 5，粒子维数D=8，加速因子

设以角度的逆时针旋转为正，给定系统运动的初始和末端位形分别为：算法经过500次迭代求得最优解，仿真结果如图2 和图3 所示。其中，图2（a）、（b）、（c）分别为系统3个位形参数的变化规律，图3（a）、（b）分别为最优控制输入规律。从图中可以看出，机器人在设定的运动周期5s内，系统可以从初始位形运动到预先设定的目标位形，且在初始和终止时刻最优控制输入值均为零，便于利用电机实现对机器人运动的控制。求得目标函数最优值为J=696.1112。

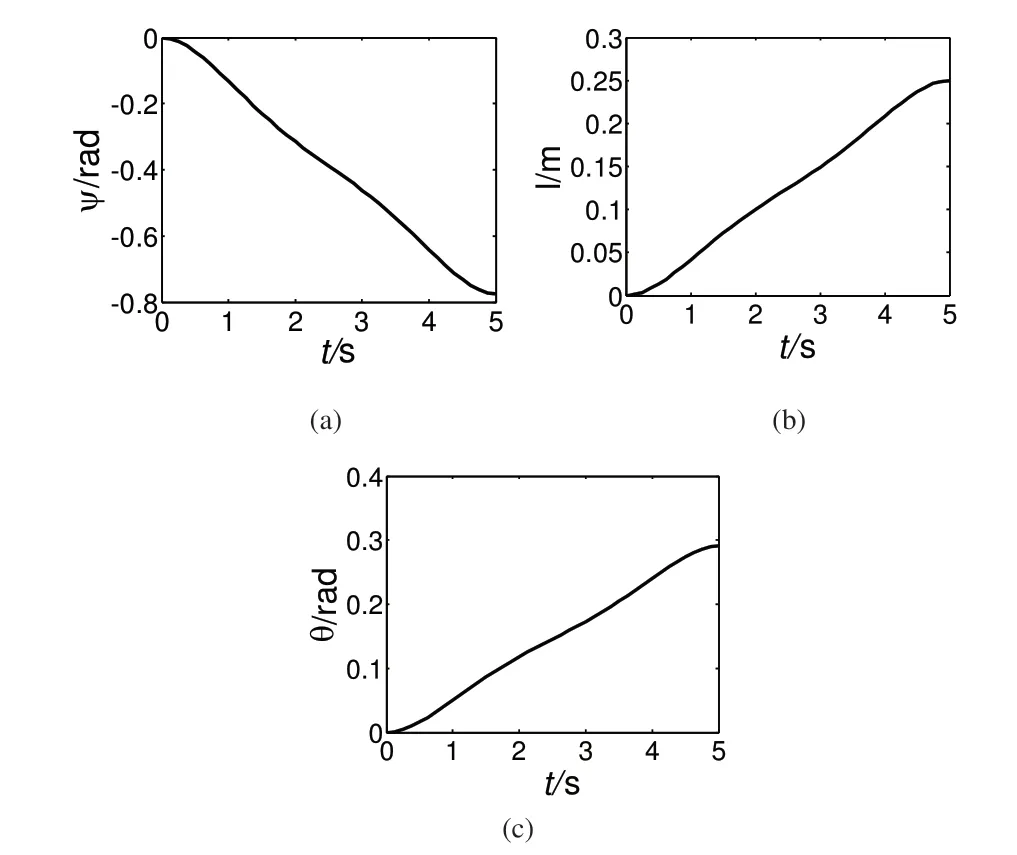
图2 单足跳跃机器人位形参数变化轨迹

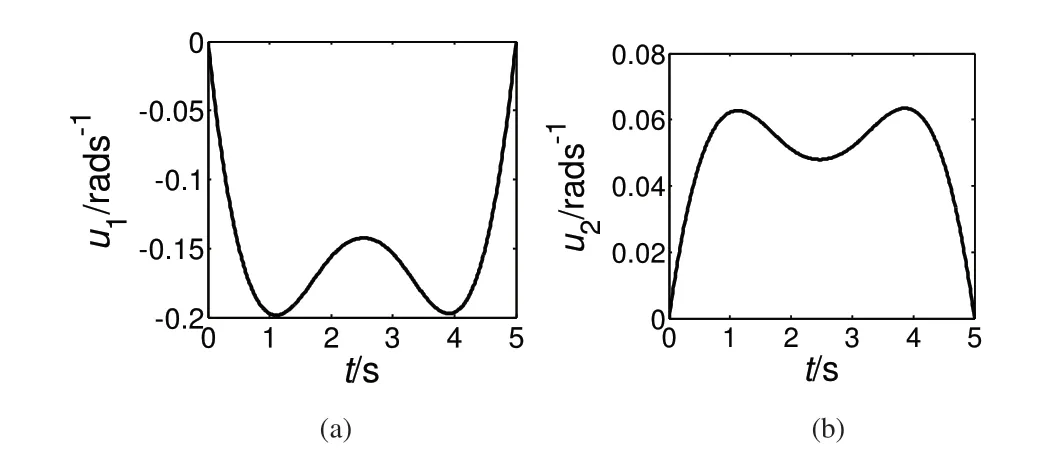
图3 单足跳跃机器人运动最优控制输入规律

5 结论

本文针对带有非完整约束的单足跳跃机器人系统模型，将样条逼近技术和粒子群优化算法引入到其姿态运动规划的最优控制问题中，求得了机器人从初始姿态运动到末端姿态的优化运动轨迹，且得到的最优控制输入的初值和终值均为零，在实际应用中，如用电机控制系统运动，则电机的初始和终止速度均为零，可方便的通过电机实现机器人姿态的运动控制。这一方法解决了利用傅里叶展开技术得到的控制输入的初始和终止速度均不为零的问题。数值仿真实验结果表明了该方法的有效性。

此外，粒子群优化算法还具有结构简单、参数较少，易于编程，收敛速度快等优点，也更适用于工程应用。同时，在运动规划中应用样条逼近控制输入是一种新的有益尝试，这一方法也为解决其他非完整系统的运动控制问题提供了一个有效的新途径。

[1] Raibert M H. Legged robots that balance[M].The MIT Press, Cambridge:MA,1986.

[2] 李保江,朱剑英.弹跳式机器人研究综述[J].机械科学与技术, 2005,24(7): 803-807.

[3] Koditschek D E, Buhler M. Analysis of a simplified hopping robot[J].International Journal of Robotics Research, 1991, 10(6): 587-605.

[4] 葛文杰,沈允文,杨方.仿袋鼠机器人跳跃运动步运动学[J].机械工程学报,2006,42(5):22-26.

[5] 杨文纲,陆震,单足跳跃机器人动力学建模与仿真[J].机械与电子,2006,(10):45-48.

[6] 赵明国,裘有斌,陈向,李嘉.单足气动跳跃机器人的基于时间事件控制方法[J].机器人, 2012,34(5) : 525-530.

[7] 杨莉莉.跳跃机器人非完整运动规划的数值算法研究[J].制造业自动化,2013,35 (7):86-89.

[8] Murray R M, Sastry S S. Nonholonomic motion planning: steering using sinusoids[J].IEEE Transactions on Automatic Control.1993,38(5):700-716.

[9] 苏鹏,何广平,徐明.基于能量最小耗散原则的跳跃机器人运动仿真研究[J].机械设计与制造,2012,(4):171-173.

[10] 曾建潮,介婧,崔志华.微粒群算法[M].北京:科学出版社, 2004.

[11] 杨莉莉.不确定性机器人轨迹跟踪控制的粒子群算法[J].制造业自动化,2013,35 (9):80-82.