基于相量分析法变压器外特性研究

戴成梅,刘 伟

在低压配电系统中,人们经常使用变压器进行电能的传输和分配,以保障各种用户能够方便地获取电能.通常,变压器所带负载主要分为电阻性负载、电感性负载和电容性负载.在正常供电状态下,当负载电流不断增加时,变压器外特性会显现出一定的变化特点,并且该特点还受到所带负载性质的影响.在大多数含有变压器内容的教材或期刊中,许多作者只简单介绍变压器的外特性变化特点,没有清楚阐述产生这种变化特点的原因,尤其负载性质对其影响的原因,以至于部分老师在授课时仅介绍变压器外特性变化特点,最多说明变压器的外特性与负载的功率因数有关.至于原因,几乎不讲.长期以来,如何解释变压器外特性产生的原因一直是件令人困惑的事情.结合自己多年的电工学理论教学经验,笔者利用相量分析法深入分析变压器外特性变化及其受负载性质影响的原因[1-3].

1 变压器副边电路分析

在图1中,Z0为变压器副边绕组的阻抗,设Z0=R0+j X0.当变压器出厂后,Z0就几乎不变.ZL为负载阻抗,令ZL=RL+j XL分别是变压器副边绕组感应电动势、变压器输出端电压和输出电流.在图1中,

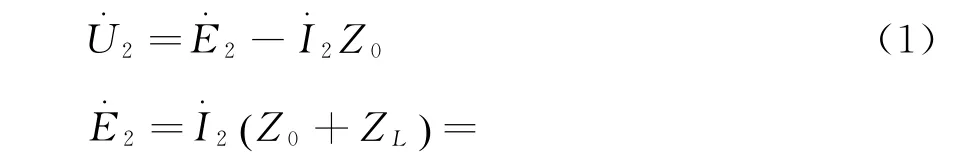
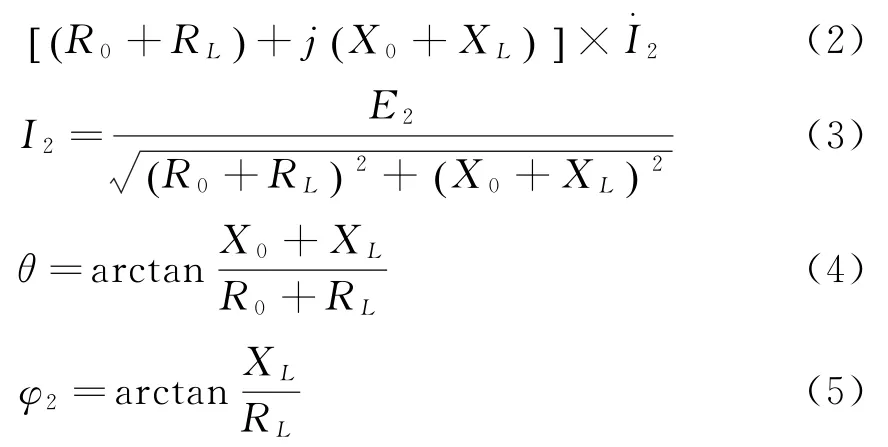
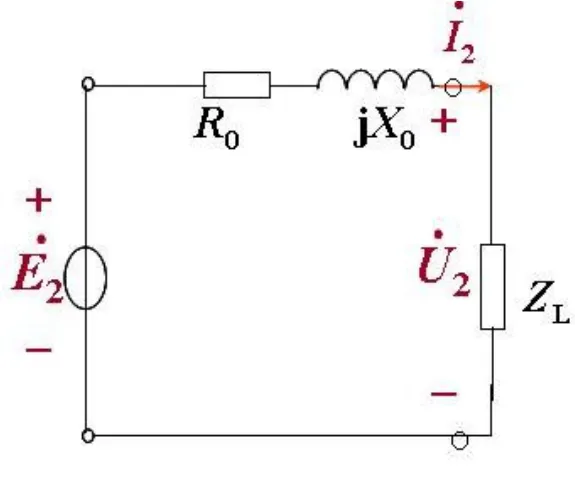
图1 变压器副边电路原理图

2 变压器外特性分析

当变压器处于负载运行时,若保持变压器原边电压U1和负载功率因数cosφ2不变,则变压器副边输出端电压U2随着输出电流I2的变化而变化.其中U2和I2函数关系称为变压器的外特性.通过实验,可以测得变压器外特性曲线,见图2.其中曲线1、2、3分别反映变压器带电感性负载、电阻性负载和电容性负载时外特性曲线.曲线1和曲线2中,U2都是随着I2的增加而下降,曲线1下降得比曲线2还快;曲线3则随着I2的增加而上翘[5].下面,利用相量分析法详细分析3条曲线变化原因及其受负载性质的影响.

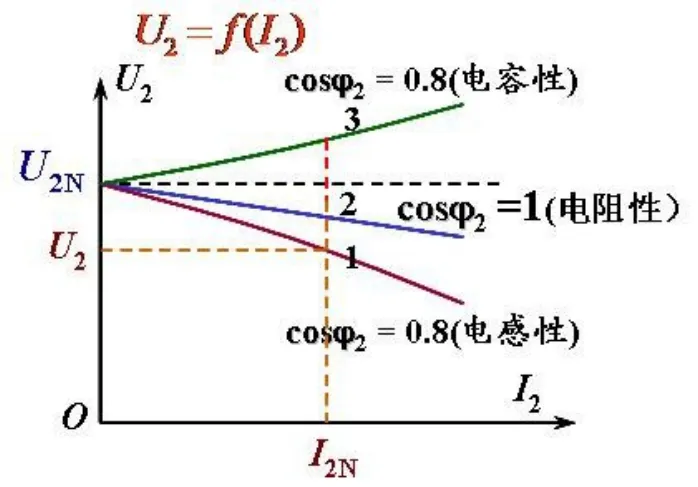
图2 变压器外特性曲线图

2.1 变压器带电阻性负载外特性分析

当变压器带电阻性负载时,图1中的ZL=RL,则负载功率因数角φ2=0,但内功率因数角θ≠0.设图1中的=E2∠00,变压器的输出电压U2和负载RL关系的推导过程如下:

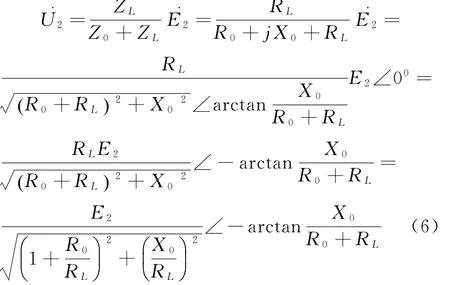
由式(6)得出变压器输出的端电压U2有效值为:

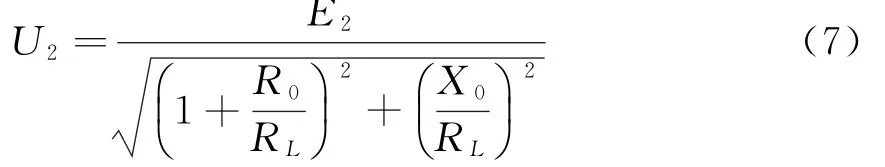
在测量变压器外特性时,由于始终保持原边电压有效值U1不变,所以主磁通的有效值也保持不变,则E2也始终保持不变.在实验中,通过减小RL阻值来实现I2不断增加,即RL↓→I 2↑,并且,根据式(7)可得出.又因为当负载正常工作时,不等式始终成立,根据式(7)可知,当变压器带阻性负载正常工作时,U2＜E2.而当变压器处于开路时,即RL=∞时,根据式(7)可得U2=E2;若变压器处于短路时,即RL=0时,根据式(7)可得U2=0.

通过上述分析可知,当变压器带阻性负载工作时,随着I2增加,其输出端电压U2呈下降趋势.并且,当I2=0时,U2=E2.这些变化特点与图2中曲线2描绘的完全一致.由此可见,利用相量分析法可以正确解释变压器带阻性负载的外特性变化原因.

2.2 变压器带感性负载外特性分析

当变压器带感性负载时,图1中的ZL=RL+j XL,设=E2∠00.当N1、f1、U1保持不变时,Φm保持不变,E2也保持不变[6].在实验中,保持不变,即=arctan保持不变.因此,在数据处理中,可设=K(K为常数),即XL=K RL.与2.1节分析原理类似,变压器的输出电压U2和负载ZL关系推导如下:

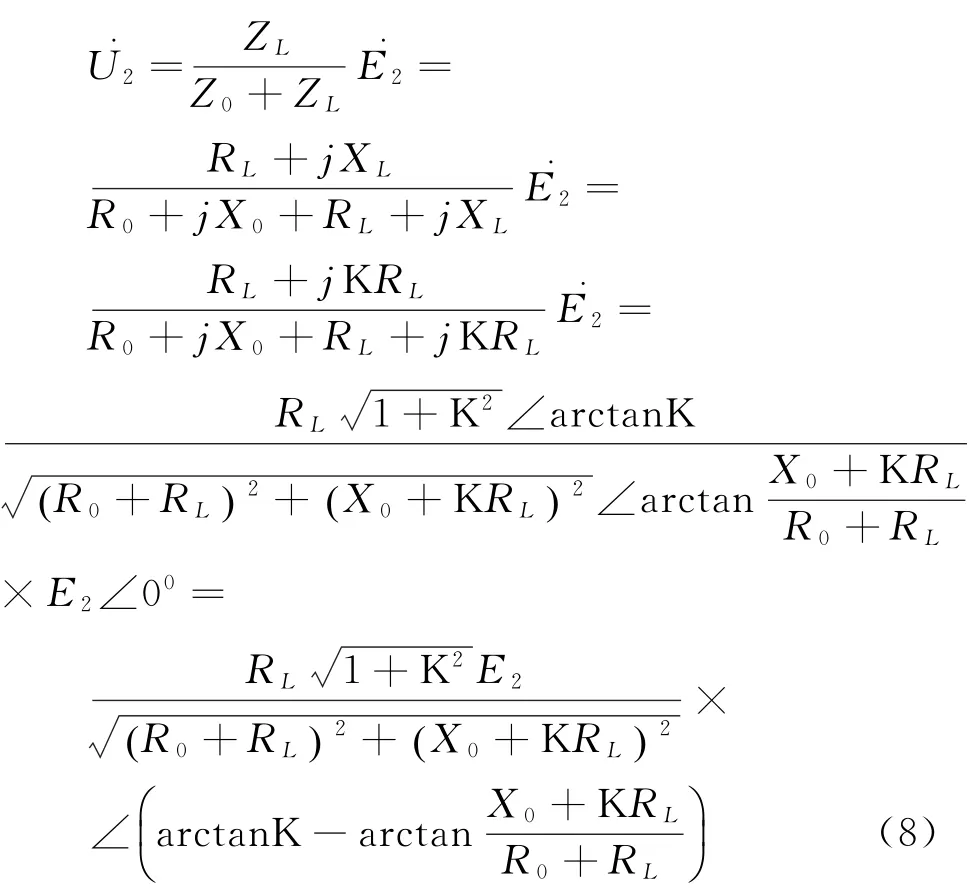
由式(8)得出变压器输出端电压U2有效值为:

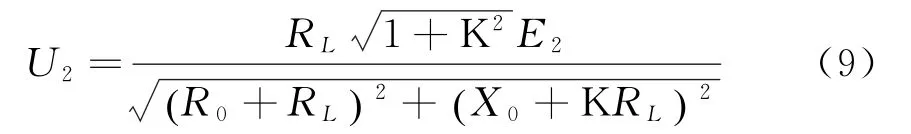
将式(9)继续整理如下:

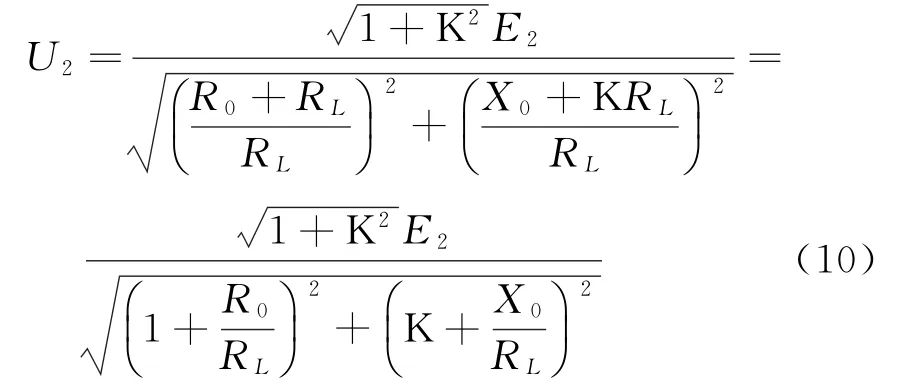
在测量变压器外特性时,E2始终保持不变.在实验中,通过减小ZL阻值来实现I2不断增加.由于ZL=RL+j XL=RL+j K RL(K为常数),所以直接减小RL可以实现ZL的减小,即RL↓→ZL↓→I 2↑.并且,根据式(10)可知,↑→U↓.另外,当变压器负载运行时,式(10)2中＜1,由此可得,U2＜E2;而当变压器处于开路时,即RL=∞时,I2=0,根据式(10)可得U2=E2;若变压器处于短路时,即RL=0时,根据式(10)可得U2=0.

通过上述分析可知,当变压器带感性负载工作时,随着I2增加,其输出端电压U2呈下降趋势.并且,当I2=0时,U2=E2.这些变化特点与图2中曲线1描绘的完全一致.由此可见,利用相量分析法同样可以正确解释变压器带感性负载的外特性变化的原因.

2.3 变压器带容性负载外特性曲线分析

当变压器带容性负载时,图1中ZL=RL-j XL.在测量变压器外特性时,保持U1、cosφ2不变,即保持不变.因此,在数据处理中,(K为常数),即XL=K RL.其中XL=在实际应用中,电容C通常为μF级或p F级,当变压器输出中低频交流信号时,电容对信号会产生很大的阻抗,而且XL≫RL,即K≫1.与2.1节分析原理类似,变压器的输出电压U2和负载ZL关系推导如下:

由式(11)可得出变压器输出的端电压U2有效值为:

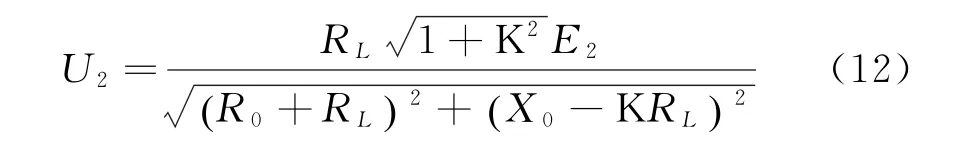
将式(12)进一步整理如下:

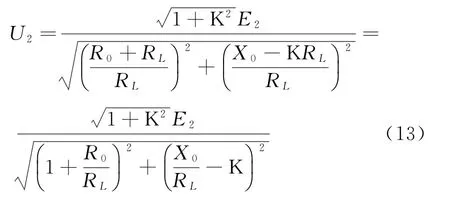
因为K≫1,所以式(13)可以近似为:

在测量变压器外特性时,E2始终保持不变.在实验中,通过减小ZL阻值来实现I2不断增加.由于ZL=RL-j XL=RL-j K RL(K为常数),所以直接减小RL可以实现ZL的改变,即RL↓→ZL↓→I2↑ .并且,根据式(14)可知,(K→U2↑ .同时,式(14)中,因此,当变压器负载运行时,U2＞

E2.另外,若变压器处于开路时,即RL=∞时,I2=0,此时,根据式(14)可得U2=E2;若变压器处于短路时,即RL=0时,根据式(14)可得U2=0.

由以上分析可知,当变压器带容性负载工作时,随着I2增加,其输出端电压U2呈上翘趋势.并且,当I2=0时,U2=E2.这些变化特点与图2中曲线3描绘的完全一致.由此可见,利用相量分析法可以正确解释变压器带容性负载的外特性变化原因.

2.4 变压器带三种负载的外特性比较

由图2可知,变压器带三种负载的特性曲线排列自上而下顺序分别为:容性、阻性和感性.即当I2取相同值时,三条曲线对应的U2是不等的,即U2C＞U2R＞U2L(U2C、U2R和U2L分别为图2中三条曲线上I2所对应的U2值).这种现象很令人费解,老师在授课时也很难讲清楚,只能解释变压器的外特性还受负载性质影响,或者说,变压器的外特性与负载的功率因数有关,仅此而已.下面,通过相量分析法详细分析产生该现象原因.

在变压器外特性比较分析过程中,图1中的E2、Z0、I2保持不变,并设=E2∠00,变压器副边绕组阻抗Z0=R0+j X0=Z0∠α.下面,分别讨论三种不同性质的负载如何影响变压器的输出端电压U2的大小.

2.4.1 变压器带阻性负载

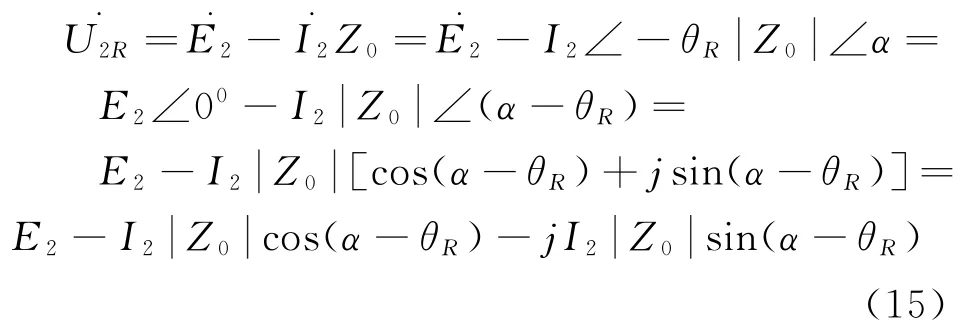
由式(15)可得:

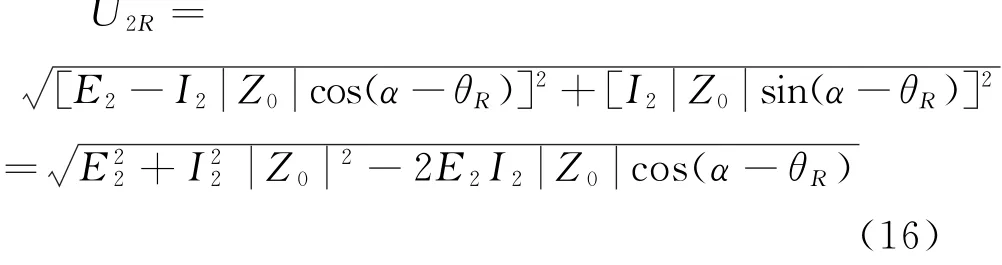
2.4.2 变压器带感性负载

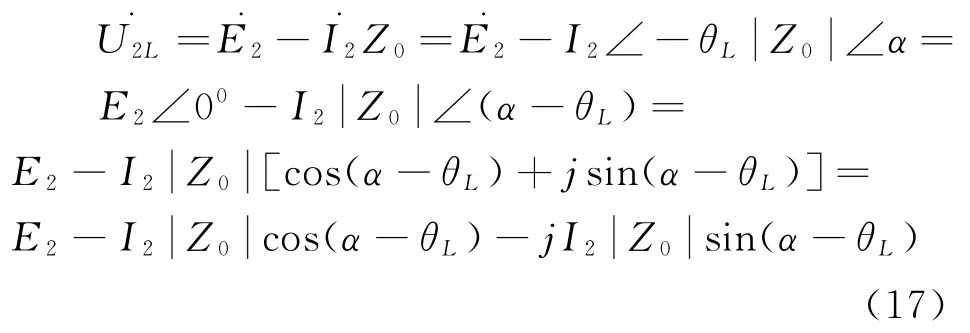
由式(17)可得:

2.4.3 式(16)中θR和式(18)中θL大小比较分析

在图1中,当负载为阻性时,θR为与之间的相位差;当负载为感性时,θL为与之间的相位差.设阻性负载ZL=RRL,感性负载ZL=RLL+j XL.当电源E2、Z0和电流I2保持不变,下面推导θR和θL之间的大小关系.当负载为阻性时,由式(3)可得:

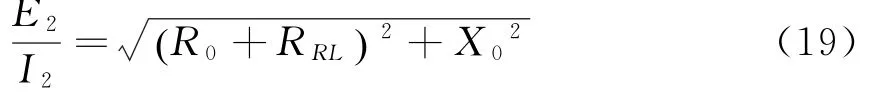
同理,当负载为感性时,可得

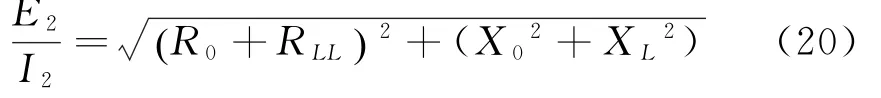
比较式(19)和(20),可得

又根据式(4)可得

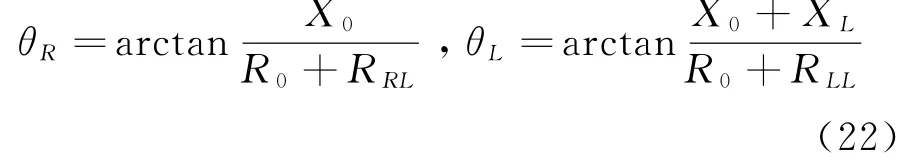
由式(21)和(22)可推出

2.4.4 变压器带容性负载

由于变压器是传递电能设备,其工作效率一般大于95%,即内部功率损耗很小.所以,ZL远大于Z0,即XL远大于X0.又根据,..,.可知θC＜0即I2比E2超前θC角.因此 可设I2=I2∠θC,则得

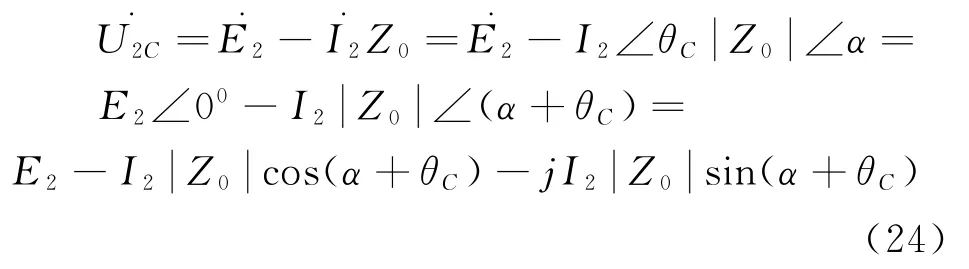
由式(24)可得

结合式(23),可得α+θC＞α-θR＞α-θL.因此,综合比较式(16)(18)(25),三式中E2、I2、Z0、α均为常数且相等,由此可得,U2C＞U2R＞.

通过上述分析可知,当变压器带负载工作时,其输出电流有效值I2任取某值且保持不变时,其输出端电压有效值U2的大小直接受负载性质影响.其中带容性负载时,U2最大,阻性负载次之,感性负载最小,即U2C＞U2R＞U2L.当I2不断增加时,该变化规律始终保持不变,进而形成三种不同的外特性变化趋势,正如图2中排列顺序,自上而下依次为容性负载、阻性负载和感性负载三种外特性曲线.

3 结束语

变压器处于负载运行时,随着负载电流增加,其外特性表现一定变化特点,而且该特点还受负载性质的直接影响.究其原因,无论从电路分析方法还是从能量方面都很难清楚解释产生该特点的原因.本文利用相量分析法详细分析了变压器三种外特性变化原因及其负载性质对其影响的原因.分析结果表明,用相量分析法分析变压器外特性变化特点与实验中所测的外特性曲线变化规律完全一致.因此,相量分析法可以正确解释变压器外特性变化原因及其负载性质对变压器外特性的影响.

参考文献:

[1]王铁.浅谈相量分析法在负荷六角图中的应用[J].沈阳工程学院学报,2013,9(2):147-150.

[2]赵小妹,丁万新,杨松,等.实用于Yd接线变压器的实用快速相量分析法[J].电工技术,2014(8):7-9.

[3]顾建华,兀雁冰.用相量分析法测试电压互感器的接线[J].电世界,2011(12):5-7.

[4]郭木森.电工学[M].北京:高等教育出版社,2010.

[5]唐介.电机与拖动[M].北京:高等教育出版社,2010.

[6]方厚辉,谢胜暑.电工技术[M].北京:北京邮电大学出版社,2010.