基于燃面耦合传热的固液发动机内流场模拟方法①

孙得川，张梦龙

(大连理工大学 航空航天学院 工业装备结构分析国家重点实验室，大连 116024)



基于燃面耦合传热的固液发动机内流场模拟方法①

孙得川，张梦龙

(大连理工大学 航空航天学院 工业装备结构分析国家重点实验室，大连 116024)

针对固液火箭发动机中的燃烧流动，建立了一种基于流场与固体燃料之间耦合传热和PDF燃烧模型的通用计算模型。应用该模型计算了二维固液实验发动机燃烧室，得到了燃烧室内部的扩散燃烧和燃面退移速率。计算得到的燃面退移速率与实验结果吻合较好，说明该方法对固液火箭发动机内流场计算有较强的通用性，PDF模型可有效模拟混合发动机中的扩散燃烧过程；简化的一维燃面传热耦合方法可应用到多维计算；该模型可用来模拟固液发动机的内弹道和预示退移速率。

固液火箭发动机；退移速率；热耦合；PDF模型；数值模拟

0 引言

在固液混合火箭发动机工作过程中，液体氧化剂通过喷注器流进含有固体燃料药柱的燃烧室。固体燃料表面因受到高温氧化剂的传热和辐射而迅速热解，热解气体与附面层内的氧化性气体相互掺混进行扩散燃烧[1]，并在附面层内形成火焰区。固液发动机燃面附近的物理化学过程非常复杂，涉及到高温氧化剂与燃料气体的燃烧反应，燃面受到传热和辐射换热的持续热解过程，以及燃料表面热解导致燃面不断退移过程等[2]。在燃烧过程中，燃烧的增强会加剧燃料热解，而热解的增强又会影响近壁区域的流动和燃烧。因此，完整的数值仿真不仅要考虑复杂化学反应机理，还要包含动网格和流动与传热的耦合过程等。

因为燃烧过程直接影响燃料退移速率，进而影响发动机内弹道。所以，固液发动机内流场计算的关键就是燃烧的模拟。目前，关于固液发动机中扩散燃烧的数值模拟，多以简单的化学反应机理为主。例如，文献[3-5]所研究的固液火箭发动机的计算模型中，燃烧模型均采用涡耗散燃烧模型，化学反应均为简单的两步反应。计算结果显示，温度峰值均比热力学理论计算结果要高，这会直接导致计算得到的退移速率过高。导致温度超过理论值的主要原因是燃烧机理过于简化。理论上讲，固液发动机中的燃料多为碳氢燃料，热解气体成分复杂，化学反应机理往往包含几十个甚至几百个基元反应，不仅过于复杂，而且其计算量巨大，难以实现。即使对于某种燃料找到了适合计算的简化燃烧模型，但一旦更换推进剂，就必须重新寻找恰当的反应模型。由此可见，燃烧模型是固液发动机数值模拟中最困难的选择。另外，固液发动机中的燃面在工作过程中不断退移，复杂数值模拟理应考虑使用动网格技术。例如，Antonis Antoniou等[6]采用动网格技术模拟了燃烧器中流动与传热的耦合过程，得到了不同时间的燃面退移以及燃料药柱表面的燃烧情况。但目前动网格技术尚未完善，计算中燃面退移会导致网格不断变化和扭曲，容易出错，大大增加数值模拟的复杂程度和计算时间，对于复杂型面更是如此。

针对以上问题，本文从能量平衡和流固耦合的角度综合考虑了发动机工作工程中各复杂物理过程，基于PDF燃烧模型和燃面耦合传热，建立了固液火箭发动机燃烧流动计算的通用模型，可较真实地模拟固液发动机中的燃烧与流动，较好地预测燃面退移速率，从而为发动机内弹道计算和燃烧室设计提供依据和支持。

1 物理模型

1.1 假设

固液混合火箭发动机的工作过程是典型的三维非定常过程。为了简化分析过程，对流场作如下假设[7]：

(1)流场为准定常。对于流动问题，因为燃料退移速率很小，而气体流动的响应很快。所以，可假设发动机工作的任一时刻气相流动为定常。

(2)温度场为准定常，且只考虑燃面法向的传热。即对于温度场，当燃料表面以恒定速率退移时，燃气一侧的温度分布和燃料一侧的温度分布保持不变。

(3)仅考虑气相燃烧。虽然在大雷诺数工况下，根据大涡理论，没有反应的氧化剂会穿过火焰面而到达固体燃料药柱表面，发生异相燃烧；但燃料热解气体的“吹风”效应，使得氧化剂气体很难到达燃料表面。

(4)混合气体为理想气体。满足状态方程p=ρRT，R是各气体的平均气体常数。气体各组分的气体常数R不随温度等变化，而比定压热容cp是温度的函数。

(5)各组分的扩散系数相同。

(6)不考虑重力等彻体力的影响。

1.2 燃烧模型

固液发动机的燃料通常为碳氢燃料，热解成分复杂，而碳氢燃料的燃烧机理也非常复杂。例如，HTPB的高温分解产物在燃烧过程中，涉及到50多种化学组分，数百个基元反应，若采用简单的总包反应，忽略燃烧中间过程和产物，会导致模拟燃烧的温度过高。因为燃烧温度直接影响传热，进而导致过高的退移速率。所以，要么采用详细的燃烧机理，要么就不能使用简化的反应模型。

因固液火箭发动机燃面附近的燃烧过程属于典型的扩散燃烧，化学反应速率主要受燃料和氧化剂气体的湍流扩散过程控制，而PDF(Probability Density Function)模型是求解湍流控制燃烧的较好模型。其中，设瞬时反应率为2个变量(温度和混合物分数或温度和氧浓度)的函数，而不需要详细的化学动力学机理，尤其适合于湍流扩散火焰的模拟和类似的反应过程。因此，本文采用PDF模型进行燃烧模拟。

图1给出了采用PDF模型计算HTPB与N2O(分解为N2和O2)混合燃烧时反应温度与HTPB浓度的对应关系，其最高温度约为3 300 K，比较符合实际燃烧情况。

1.3 燃烧表面的传热

燃料的退移速率受流动和传热的影响。根据假设，当燃料表面以恒定速率退移时，燃气一侧的温度分布与燃料一侧的温度分布保持不变，如图2所示。

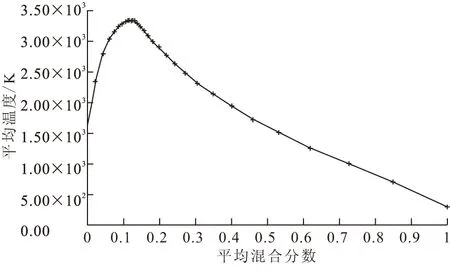
图1 PDF温度分布Fig.1 Temperature magnitude distribution of PDF

图2 燃料表面附近的温度分布Fig.2 Temperature distribution near solid fuel surface

另外，假定燃料热解气体离开表面时的温度与燃料表面温度相同。在燃料表面，存在热流平衡：

qg+qr=qd+qs

(1)

(2)

计算中，在流场迭代求解的每一步求解公式(1)，可得到迭代过程中的退移速率 ，当满足收敛条件后， 也达到稳定解。关于燃料表面耦合传热的详细计算见文献[9]。

1.4 湍流模型

固液火箭发动机燃烧室的流动一般是湍流流动，由于固体燃料表面的退移速率非常小，燃料热解气体加入的速度很低，基本类似于壁面。因此，计算湍流时，应把燃面作为壁面处理。

在两方程湍流模型中，无论是标准k-ε模型、RNGk-ε模型，还是Realizablek-ε模型，都是针对充分发展的湍流的，这些模型均是高雷诺数湍流模型，多用于求解处于湍流核心区的流动。而在燃面附近，流动几乎是层流，采用k-ω模型求解会存在较大误差。因此，许多文献应用低雷诺数模型来计算燃面附近的流动。但低雷诺数湍流模型对燃面附近的网格提出了较高的要求，一般要求壁面第一层网格的y+≈1。因此，若采用低雷诺数模型，当氧化剂流量较大(平行于壁面的速度较大)时，壁面第一层网格很小，导致时间步长很小，收敛过程很慢。

因k-ω模型综合考虑低雷诺数、可压缩性和剪切流传播，适合应用于墙壁束缚流动和自由剪切流动，而剪切应力传输(SST)k-ω模型则充分采用了k-ε模型在远壁面区域求解中的优点和标准k-ω模型在近壁面区域求解中的优点，具有更广的应用范围和更高的模拟精度。所以，本文采用SSTk-ω模型。

SSTk-ω模型输运方程如下：

式中Gk为湍流的动能；Gω为ω方程；Γk、Γω分别为k与ω的有效扩散项；Yk、Yω分别为k与ω的发散项；Dω为正交发散项。

2 计算模型

2.1 计算区域和网格

本文以某实验发动机为研究对象。如图3所示，沿氧化剂流动方向依次为预燃室、药柱、补燃室、喷管。其中，药柱为内孔燃烧，初始内径为30 mm。本文中，固体燃料为HTPB，密度为1.27 g/s，液体氧化剂为N2O，流量为0.4 kg/s。总的网格数目为81 022个，其中燃烧通道内网格为结构网格，壁面第一层网格厚度为0.05 mm。

图3 固液发动机简图和网格Fig.3 Schematic and mesh of the hybrid rocket motor

2.2 数值方法

流场计算采用FLUENT，固体传热采用中心差分格式计算；压力求解采用基于不可压缩流的PISO算法；控制方程采用有限体积法离散。其中，对流项和扩散项均采用二阶迎风格式离散。燃面上采用UDF编程，通过热流平衡进行耦合。

2.3 边界条件

氧化剂入口和燃面边界条件均采用采用质量流量入口。

假设氧化剂在入口处已经完全分解为氮气和氧气，根据热力计算结果，氧气质量占0.36，氮气质量占0.64，混合气体温度为1 600 K。

表1 HTPB在1 023 K下的热解气体成分Table1 Species of pyrolysis gas of HTPB at 1 023 K

出口边界条件采用压力出口条件。壁面采用无滑移、绝热壁面边界条件。

3 算例验证

为验证计算模型的合理性和正确性，本文针对文献中的固液混合发动机实验进行验证计算。

3.1 算例1

采用文献[10]中的第9次实验数据进行验证。文献中燃烧室为二维平板结构，燃烧室上、下两药柱表面间距20 mm，气氧流量为0.2 kg/s。图4给出了采用本文模型得到的退移速率。从图4可看出，计算结果与实验结果吻合较好，退移速率沿流动方向逐渐增大。

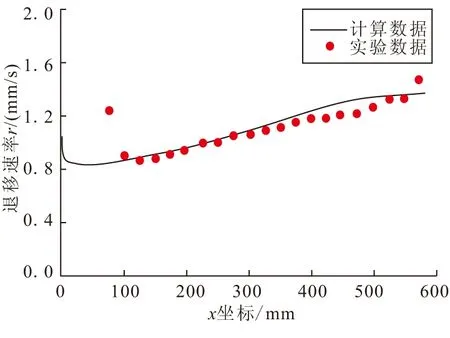
图4 计算结果与实验结果对比Fig.4 Comparison of test data with calculation results

3.2 算例2

文献[11]中的实验发动机以气氧(GOX)为氧化剂，高密度聚乙烯HDPE(C2H4)为燃料。燃料药柱为圆柱形，内孔燃烧，初始药柱内径为10 mm。文献给出了发动机工作10 s后得到的沿轴向的退移速率和整个燃面的总平均退移速率(0.61 mm/s)。考虑到发动机工作过程中，随着燃烧通道面积的变化退移速率会改变，且实验发动机药柱沿轴向的退移速率相差不大，故本文对发动机在不同工作时刻的流场进行计算。计算中取燃料内孔直径分别为10、14、16、18、20、22.2 mm。通过对不同内孔对应的退移速率进行时间加权平均，得到沿轴线方向的退移速率与实验值对比见图5。

图5 计算结果与实验结果对比Fig.5 Comparison of test data with calculation results

由图5可见，计算结果与实验结果吻合较好。文献[11]中给出的总平均退移速率为0.61 mm/s，本文计算得到的总平均退移速率为0.64 mm/s，十分接近实验值。

通过2个算例数据对比可知，采用本文的数值模型能够较好地模拟固液混合发动机实验，并预测燃料退移速率。

4 计算结果分析

根据实验结果，本文计算的固液发动机工作时间约为10 s，平均退移速率约为2 mm/s。为了讨论燃面耦合传热在数值模拟中的作用，本文分别进行了指定燃面退移速率和燃面耦合传热2种计算。

4.1 指定退移速率

根据HTPB燃料退移速率公式(2)，当燃面温度Ts>722 K时，Ea=4.91 kcal/mol，A=11.04 mm/s。退移速率与燃面温度的关系曲线如图6所示。

图6 HTPB退移速率与表面温度的关系Fig.6 Relationship between regression rate and fuel surface temperature of HTPB

因为发动机的长径比较大，为方便观察，下面各图均将径向坐标放大2倍。图7给出了燃烧室内的速度幅值分布。可见，在药柱通道内的速度较高。

图7 速度分布Fig.7 Velocity magnitude distribution

图8给出了燃烧室内的温度分布，可观察到燃烧是典型的扩散燃烧，温度分布不均匀，高温火焰区域呈带状分布。燃烧发生在燃料通道和补燃室中，即氧化剂和燃料热解气体混合反应的区域，最高温度为2 850 K。在燃料通道内，因为通道较窄，燃气速度高，故轴线附近区域主要是氧化气体(高温氧气和氮气混合物)，温度接近氧化剂进口温度1 600 K，会对前室结构产生较强的氧化作用；另外，因为高温氧化气体速度很高，迫使火焰紧贴燃面；燃烧火焰主要呈现带状区域分布，火焰区域以外温度相对低一些。

图8 温度分布Fig.8 Temperature magnitude distribution

4.2 考虑燃面耦合

对考虑燃面传热耦合的燃烧计算，燃面退移由燃料药柱表面的热流决定，即退移速率受流动和燃烧的温度场控制。实验过程中发现，退移速率沿轴向比较接近。所以，分别对燃料药柱内径为30、40、50、60 mm的情况进行了计算。

图9和图10分别给出了4种药柱内径的的温度场和燃料热解气体浓度分布。从中可观察到：燃烧发生在燃料通道和补燃室中，前室主要为氧化剂分解气体(高温氧气和氮气混合物)，其温度为1 600 K左右，是N2O分解后的温度；燃烧通道内的燃烧属于典型的扩散燃烧，因为燃烧通道狭窄，高温氧化气体速度很高，迫使火焰紧贴燃面；而高温燃气和氧化气体进入补燃室，则类似于高速射流，流速非常高；随着燃料药柱内径的不断增大，氧化剂和燃料深入补燃室的距离越来越长，最高温度也越来越高。

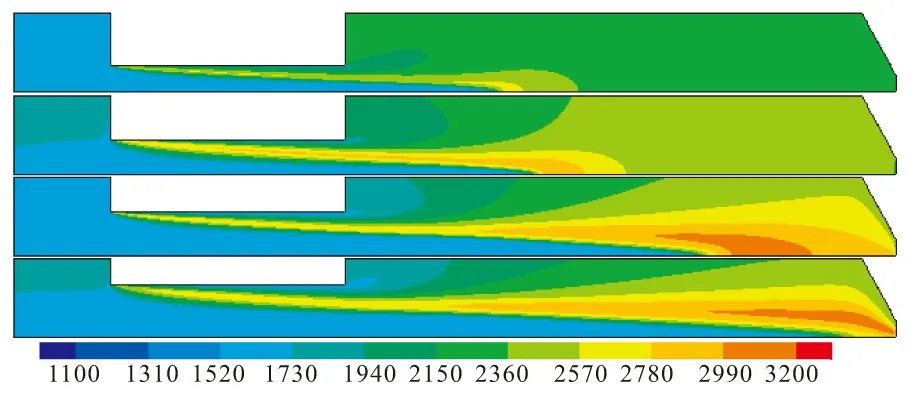
图9 温度分布Fig.9 Temperature magnitude distribution

图10 燃气质量分数Fig.10 Mass fraction of fuel gas

从图10可见，随燃烧通道的扩大，在发动机工作后期，会有部分氧化剂气体未参与反应就喷出发动机，这既造成氧化剂的浪费，也加剧对喷管的氧化烧蚀。

图11给出了不同直径的燃料内孔所对应的退移速率分布情况。可见，靠近氧化剂进口位置的退移速率较高，随着向燃烧室下游的流动，退移速率均有所下降。另外，随着燃烧通道直径的增大，退移速率整体下降。不同通道直径所对应的平均退移速率分别为2.429、2.098、1.694、1.5 mm/s。燃料上游退移速率高的原因是扩散燃烧火焰紧贴燃面，高温火焰与燃面之间的温度梯度很大，对流换热很强，造成前端退移速率较高。随着向下游流动，扩散火焰区逐渐远离燃面，对流换热逐渐减小。所以，退移速率逐渐下降。当燃烧通道直径增加时，通道内的流速降低，火焰前锋与燃面的距离增大，从而使对流换热减小，退移速率也随之减小。因此，固体燃面的温度主要取决于2个因素：一是燃烧火焰距固体表面的距离，距离越近，燃面上温度梯度越大，得到的热反馈就越大；二是随着内径的不断增大，固体药柱表面附近的气体流速减小，对流换热系数就减小，流入固体的热流也减小，从而导致退移速率降低。

图12对比了初始时刻(药柱内径为30 mm)时，分别采用指定退移速率(2 mm/s)和耦合燃面传热(平均退移速率2.429 mm/s)计算的内流场温度分布。可看到，火焰前锋进入补燃室的距离基本一致；指定退移速率所得到的温度场最高温度稍高一些。可见，当给定的退移速率接近实际值时，可近似地模拟实际流场，但这种方法不能得到退移速率随空间的变化。

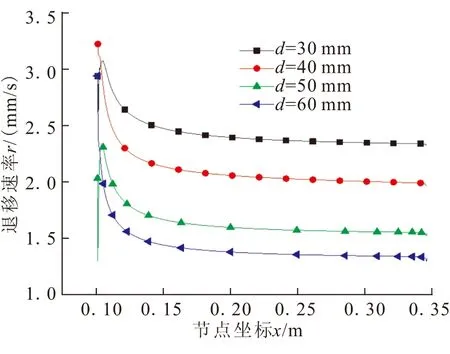
图11 不同药柱内径下的退移速率分布Fig.11 Regression rate under different channel diameter

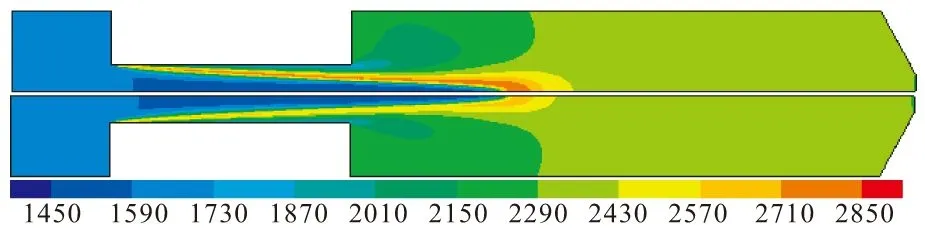
图12 温度对比分布Fig.12 Comparison of temperature magnitude distribution

5 结论

(1)所建立的数值模型能较好地模拟复杂的燃烧过程，具有较强的通用性，可用来模拟固液发动机的内弹道和预示退移速率。

(2)PDF模型可有效地模拟混合发动机中的扩散燃烧过程，得到的火焰结构和最高温度与实际较符合，

(3)燃面传热耦合方法有较强适用性，可应用到多维计算。

[1] Tsohas J,Appel B,Rettenmaier A,et al.Development and launch of the purdue hybrid rocket technology demonstrator[R].AIAA 2009-4842.

[2] 孙得川,杜新,汪亮. 热解过程对H2O2-PE固液发动机点火的影响[J].固体火箭技术,2006,29(5):346-349.

[3] 胡建新,夏智勋,张为华,等.固液混合火箭发动机简单反应流模拟[J].弹道学报,2002,14(4):19-24.

[4] 杨玉新,胡春波, 孙得川,等.基于流-固耦合的混合火箭发动机固体燃料表面退移速率计算[J].固体火箭技术,2007,30(3):214-216.

[5] 田辉,蔡国飙,王慧玉,等.固液混合火箭发动机燃烧的边界层计算[J].推进技术,2002,23(5):379-382.

[6] Antonis Antoniou,Kazim M Akyuzlu. A physics based comprehensive mathematical model to predict motor performance in hybrid rocket propulsion systems[R].AIAA 2005-3541.

[7] 孙得川,王博,夏广庆.流动参数对固液发动机燃料退移速率的影响[J].固体火箭技术,2013,36(4):496-499.

[8] Martin J Chiaverini,George C Heating,Lu Yeu-cherng,et al.Pyrolysis behavior of hybrid rocket solid fuels under rapid heating conditions[R].AIAA 97-3078.

[9] Martin J Chiaverini,Nadir Serin,David K Johnson,et al.Thermal pyrolysis and combustion of HTPB-based solid fuels for hybrid rocket motor applications[R].AIAA 96-2845.

[10] Venkateswaran S,Merkle C L.Size scale-up in hybrid rocket motors[R].AIAA 96-0647.

[11] Jungpyo Lee,Soojong Kim,Gihun Kim Heejang Moon,et al.A study on burning rate with mass transfer number (B number) of solid fuel in a single port hybrid rocket[R].AIAA 2010-7032.

(编辑：崔贤彬)

Simulation method for hybrid rocket motor based on thermal coupling at burning surface

SUN De-chuan,ZHANG Meng-long

(School of Aeronautics and Astronautics,Dalian University of Technology，State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian 116024,China)

A general calculation model based on thermal coupling at burning face and PDF combustion model was proposed to simulate the flow and combustion in hybrid rocket motor.Two dimensional hybrid rocket motors were simulated by this calculation model and regression rate was obtained.The calculation results agree well with test data，which means the PDF model can simulate the diffusion combustion in hybrid rocket combustor and the simplified one dimensional thermal coupling method at burning surface can be used in multi-dimensional calculations.The calculation model can be widely used in hybrid rocket flowfield simulation and also be used to predict the fuel regression rate.

hybrid rocket motor;regression rate;thermal coupling;PDF model;numerical simulation

2014-07-27；

：2014-12-08。

航空基金(20120163001)，中央高校基本科研业务费专项资金。

孙得川(1973—)，男，教授，研究领域为火箭发动机。E-mail：dechuans@dlut.edu.cn

V435

A

1006-2793(2015)02-0208-06

10.7673/j.issn.1006-2793.2015.02.011