火箭引射模态下主火箭总压与RBCC发动机的匹配性①

吕 翔，郑思行，何国强，刘佩进

(西北工业大学 燃烧、热结构与内流场重点实验室, 西安 710072)



火箭引射模态下主火箭总压与RBCC发动机的匹配性①

吕 翔，郑思行，何国强，刘佩进

(西北工业大学 燃烧、热结构与内流场重点实验室, 西安 710072)

基于传统的“等压面假设”理论，建立了RBCC发动机主火箭的引射性能分析模型，研究了主火箭总压与RBCC发动机的匹配性。研究结果表明，若隔离段通道面积比小于0.65，在主火箭总压较低条件下，隔离段内二次流容易达到壅塞，无法进一步提高空气流量；在地面静止状态下，随主火箭总压增加，空气流量逐步增大，等压面上形成Fabri壅塞后，进一步增加主火箭总压，反而会降低空气流量；在火箭引射模态下，RBCC发动机的工作状态可细分为引射作用占主导地位的进气道亚临界状态和临界状态、冲压作用占主导地位的进气道超临界状态，其分界马赫数分别约为0.7和1.5。

火箭基组合循环；高超声速飞行器；火箭引射模态；主火箭；隔离段

0 引言

火箭基组合循环发动机(Rocket Based Combined Cycle, RBCC)实现了火箭发动机与双模态超燃冲压发动机的有机组合，能够很好地满足大气层内高超声速飞行任务对推进系统提出的宽包线和高性能等要求[1-4]。火箭引射模态是其低速阶段(Ma<3.0)的动力方案，利用主火箭燃气(一次流)引射作用，将总压相对较低的来流空气(二次流)引射进冲压燃烧室内，进而组织燃烧实现发动机推力增益。主火箭有效扩展了双模态超燃冲压发动机的飞行马赫数下限，保证发动机能在低飞行马赫数下以足够的空气流量产生额定推力；同时，主火箭产生的高温燃气也为冲压燃烧室内实现稳定高效燃烧提供了可靠保证。作为火箭引射模态的核心部件，主火箭的引射性能优劣直接决定了RBCC发动机推力水平，影响到发动机能否满足飞行任务提出的性能要求。因此，开展主火箭设计的前提是对主火箭与RBCC发动机的工作匹配性有充分认识。

在火箭引射模态发动机性能理论研究方面，Koupriyanov[5]、Han[6]以及本文作者等[3]基于准一维流动分析方法，建立了火箭引射模态下发动机性能分析方法。由于模型中考虑了主火箭对发动机性能的影响，因而可从发动机推力、比冲和引射比等性能参数角度分析主火箭与发动机工作匹配性。Han的研究结果[6]表明，较小的主火箭燃气分子量易于产生较高的引射比、推力和比冲，且二次流不会产生壅塞现象。本文作者在进行RBCC飞行器的轨迹设计分析方法研究时[2]，获得了主火箭质量流率随飞行马赫数的变化规律。结果表明，主火箭质量流率调节比达到了6.3，当飞行马赫数超过1.7时，引射作用占主导地位。

李强等[7]通过CFD和实验研究表明，当来流马赫数Ma<1.3时，引射量由火箭引射主导；当来流马赫数Ma>1.5时，引射量由冲压主导。Okai等[8]通过冷流实验和数值模拟，对RBCC发动机的引射工作过程进行了研究，发现主火箭过膨胀将有助于获得较高的引射比。Smith等[9]和Lineberry等[10]分别通过冷流实验发现，当主火箭室压超过一定临界值后，二次流将形成壅塞。但二者实验中主火箭室压上限分别是4.8 MPa和6.2 MPa，均未对更高室压条件开展研究。Aoki等[11]利用冷流实验和理论分析方法，研究了二次流与一次流的总压比、入口面积比以及一次流马赫数对发动机性能的影响。结果表明，总压比越大、入口面积越小，混合后的总压越高，一次流马赫数越高，对二次流的引射作用越强。

RBCC发动机中主火箭扮演了引射器的角色，因而对传统引射器的大量理论分析[12-16]可为主火箭与RBCC发动机的工作匹配性研究提供借鉴。有研究者[17-18]借鉴传统引射器的理论分析方法，研究了主火箭工作参数对火箭引射模态发动机性能的影响。对于以达到最大引射流量为目标的引射器应用来说，传统的引射器理论分析方法是非常成功的。但这些理论分析方法用于RBCC研究还存在一定的局限性，主要原因是这些模型对引射器内的流动状态附加了某种限制，如限定一次流/二次流混合后达到壅塞，或者发动机出口面上气流达到壅塞。因此，传统的引射器理论分析方法难以对主火箭与RBCC发动机的工作匹配性进行深入研究。

目前，尽管对RBCC发动机的燃烧组织和性能开展了大量研究，但对于主火箭工作参数和设计参数之间的匹配关系、相关参数的设计依据、发动机工作过程中主火箭对发动机的影响规律等，还有大量的工作需要开展。本文运用理论分析方法，通过研究不同条件下主火箭总压对RBCC发动机引射性能参数的影响，对主火箭总压与发动机的匹配性问题进行理论研究。

燃气流量是表征主火箭规模、决定其性能的重要参数，但该参数与发动机的尺寸规模密切相关。相比之下，主火箭燃气总压与尺寸规模的关系不大，可认为是相互独立的参量。对于结构尺寸一定的主火箭来说，流量与其总压成正比关系。因此，本文选择了主火箭总压作为研究参数。

1 理论分析模型

在建立主火箭引射作用理论分析模型时，本文采用了目前得到普遍认可的“等压面假设”[12-16]：在进行掺混之前，一次流(即主火箭燃气)和二次流(即空气流)在流道内经压缩或膨胀，达到压强平衡，形成一个等压面(如图1所示)。

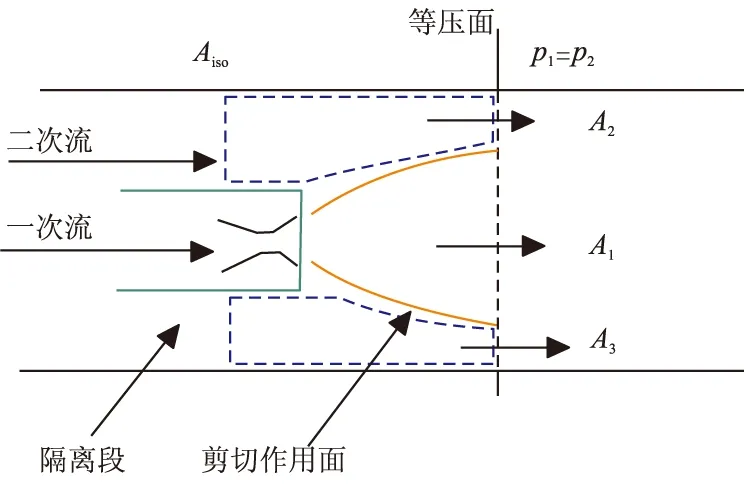
图1 主火箭引射特性分析Fig.1 Sketch for rocket ejector analysis

在实际发动机中，主火箭燃气流场存在复杂的压缩和膨胀波系、复杂的燃气/空气剪切掺混区域，主火箭燃气的流场区域很不规则。对于理论分析来说，需要忽略这些复杂特征，对其进行简化处理。因此，本文假定主火箭燃气在喷管出口与等压面之间呈现图1所示的规则分布，假定主火箭燃气区域边界呈线性变化。

针对二次流选择图1中虚线所示的控制体，根据动量定理可知，在忽略壁面摩擦力的情况下，等压面上二次流的冲量增量等于一次流对其剪切作用力，即

(1)

式中 下标0表示发动机入口；下标2表示二次流；下标3表示等压面；pc为RBCC发动机燃烧室压强，采用准一维分析方法计算获得[3]。

基于流体力学基本理论，可给出一次流对二次流的剪切作用，如式(2)所示：

Fτ=0.5βρ2f(ηαV1-V2)2Sτ

(2)

式中f为一次流与二次流之间的摩擦系数；ρ2为二次流密度；V1、V2分别为一次流和二次流速度；β为修正因子；Sτ为一次流和二次流之间剪切作用面面积。

Sτ可采用式(3)进行计算

(3)

式中De,1为主火箭喷管出口直径；Lτ为一次流和二次流剪切作用长度。

尽管主火箭燃气区域边界呈线性分布的假设与真实情况有较大差异，但由于引入了修正因子β，利用实验数据进行模型修正后，可在一定程度上改善简化假设产生的误差。

在一次流膨胀过程中，不可避免地会出现气流速度方向与发动机轴向不一致的情况，因而引入表征速度矢量方向与发动机轴向夹角对引射效应影响的系数ηα。

在等压面上有如下方程：

p1=p2

A1+A2=fAA3

(4)

式中fA为考虑剪切层厚度而引入的修正因子。

根据作者开展RBCC发动机研究的大量数值模拟结果和实验结果[7,18-19]，各经验参数取值如下：

f=0.005,ηα=0.8

βLτ=0.25,fA=0.8

补充如下的基本关系式[20]：

(5)

这样整个方程组(1)～(5)封闭可解，求解即可获得不同截面上一次流和二次流的相关参数。

采用4次典型实验数据对本模型进行了验证，对比结果如表1所示。从表1可看出，在地面静止状态下空气引射量计算值的相对误差最大，达到12.3%；当马赫数较高时，误差逐渐减小到4.07%。验证结果表明，本模型可用于开展主火箭总压与RBCC发动机匹配性研究。

2 典型流动状态分析

2.1 隔离段内二次流壅塞

如果方程组(1)～(5)求解结果出现：

(6)

式中k为空气的比热比；R为气体常数。

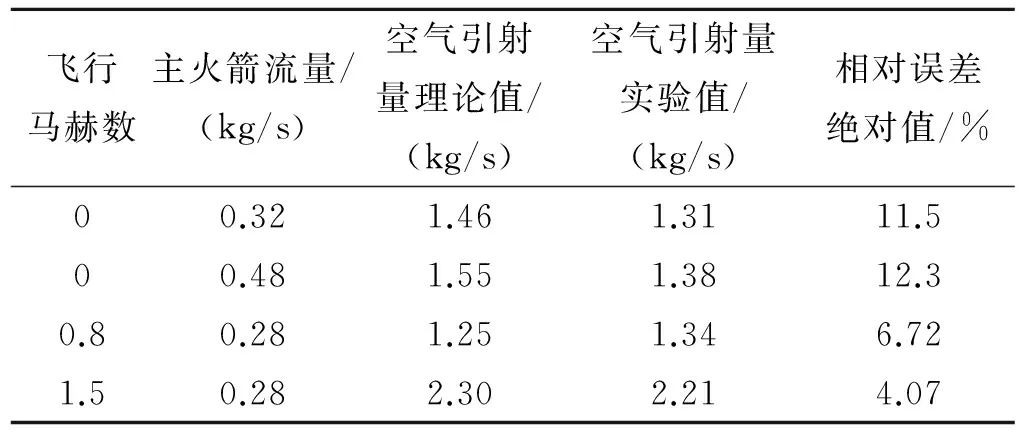
表1 理论计算与实验结果对比Table1 Comparison between analytical and experimental results

2.2 等压面上二次流壅塞

如果求解结果出现等压面上M2=1.0的情况，这意味着引射器达到了第二类临界状态[6]。出现这一现象的主要原因是主火箭总压较高，为了实现充分膨胀，等压截面上的主火箭通道面积不断增大并压缩二次流，导致其形成壅塞。由于等压面处的二次流通道相当于“气动喷管”的喉部，主火箭总压增大会引起该气动喷管喉部面积的减小，进而造成二次流流量降低，成为制约空气引射量的另一瓶颈。其解决方法是降低主火箭总压，以减弱一次流的膨胀程度。图4中，所有曲线均出现了该状态。

3 地面静止状态下主火箭总压与隔离段通道面积的匹配性

以文献[7,18-19]所采用的试验发动机构型为参考，采用表2所示计算参数，研究了地面静止状态下和不同隔离段通道面积下主火箭总压对引射性能的影响。表2中，Ar,1为主火箭喷管出口面积与喉部面积之比。为了使研究结果更具有普适性，计算中采用了无量纲的隔离段通道面积比(εiso=Aiso/A3)，计算结果如图2～图5所示。

图2和图3所示的计算结果表明，随主火箭总压增大，二次流流量先增大、后减小。若隔离段内气流形成壅塞(如εiso=0.6对应的计算结果)，主火箭总压在一定范围内增大时，二次流流量会保持恒定不变，但进一步增加主火箭总压，仍会引起二次流流量减小。

表2 主火箭引射性能计算参数Table2 Parameters for rocket ejector analysis

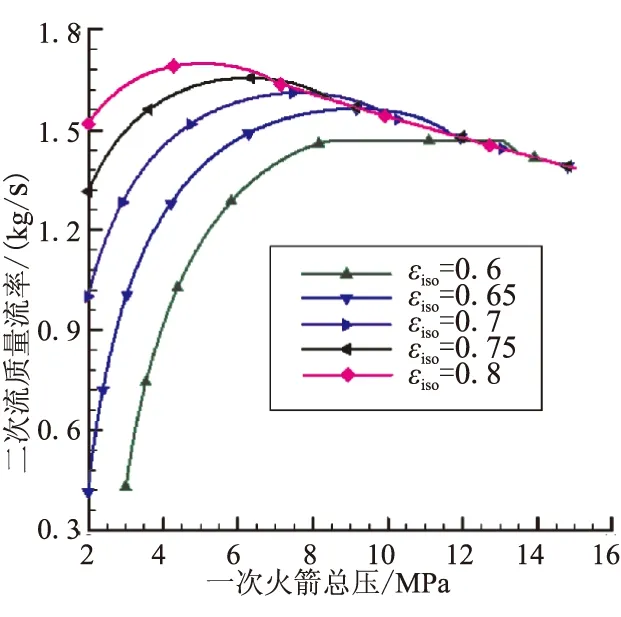
图2 二次流流量Fig.2 Mass flow rate ratio of secondary flow

图3 隔离段马赫数Fig.3 Mach number in isolator

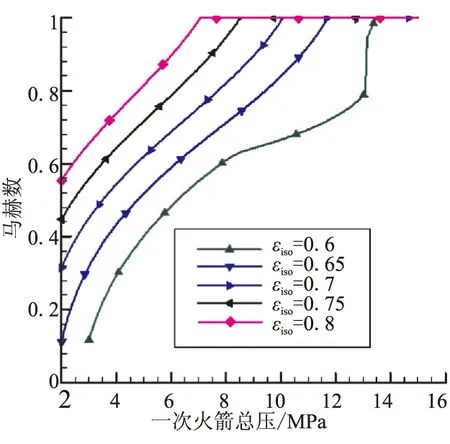
图4 等压面上二次流马赫数Fig.4 Secondary flow mach number on pressure-equal plane

由于一次流需要不断地膨胀，以达到与二次流的“等压”。因此，当增加主火箭总压时，一次流速度不断增加、两股流动的剪切作用面不断增大。式(2)表明，这将使主火箭的引射能力不断得到增强，从而表现为隔离段内气流马赫数增加、二次流流量增加。随主火箭总压不断增大，燃气膨胀程度持续增加。由图4和图5可清楚地看出，这将导致等压面上二次流通道面积不断减小、二次流不断加速直至壅塞(即Fabri壅塞)。此后，继续增加主火箭总压将，引起二次流通道面积减小，从而直接表现为二次流流量下降、隔离段气流马赫数降低。

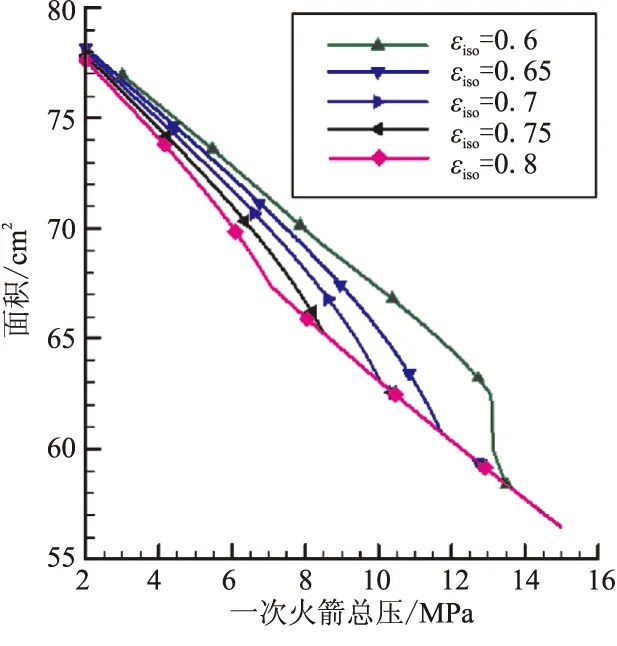
图5 等压面上二次流通道面积Fig.5 Secondary flowpath area on pressure-equal plane

如果隔离段的通道面积足够小(如图2～图5中，εiso=0.6)，持续增大主火箭总压，将会导致隔离段内气流先于等压面上二次流达到壅塞。此时，在一定范围内增加主火箭总压，不会引起二次流流量的任何变化，仅导致等压面上的二次流加速、流道面积减小。如果主火箭总压增大到导致二次流在等压面形成壅塞，进一步增大主火箭总压，会引起二次流流量下降、隔离段气流马赫数偏离壅塞状态，引射效率极低。从RBCC飞行器总体的研究结果来看，在火箭引射模态下，为了保证较高的发动机推力，需要保持较大的主火箭流量。因此，基于这一考虑，隔离段通道面积比应不低于0.65。

隔离段通道面积较大时(εiso≥0.65)，无论主火箭总压怎样变化，隔离段通道内将无法形成壅塞。此时，出现了一个需要特别注意的现象：形成二次流流量最大值的主火箭总压(见图2)总是小于形成Fabri壅塞所需要的主火箭总压(见图4)。例如，εiso=0.7时与最大二次流流量对应的主火箭总压约为pt,1=8 MPa，而形成Fabri壅塞对应的主火箭总压pt,1=10 MPa。解释这一现象的根本原因，需仔细分析流量计算公式：

(7)

式(7)中，决定二次流流量的变量为等压面上二次流面积和二次流马赫数。从图4和图5所示的等压面上二次流马赫数及二次流面积变化来看，在pt,1=8 MPa时，有：

由此看来，εiso=0.7、pt,1=8 MPa时，在等压面上由于主火箭总压增大引起的二次流流量函数相对增加幅度小于二次流面积的相对减少幅度，因而造成二次流流量随主火箭总压的增大而降低。

表3给出了不同隔离段通道面积条件下，二次流流量最大值对应的隔离段通道和等压面上二次流马赫数。由于εiso=0.6隔离段通道已经提前达到壅塞，因此表3将其除去。从表3可看出，随隔离段通道面积的增大，隔离段马赫数最大值在不断减小，而等压面上二次流马赫数在不断增大。因此，为获得最大的二次流流量，主火箭总压应保证等压面上二次流不能达到Fabri壅塞，应保证马赫数为0.8左右。

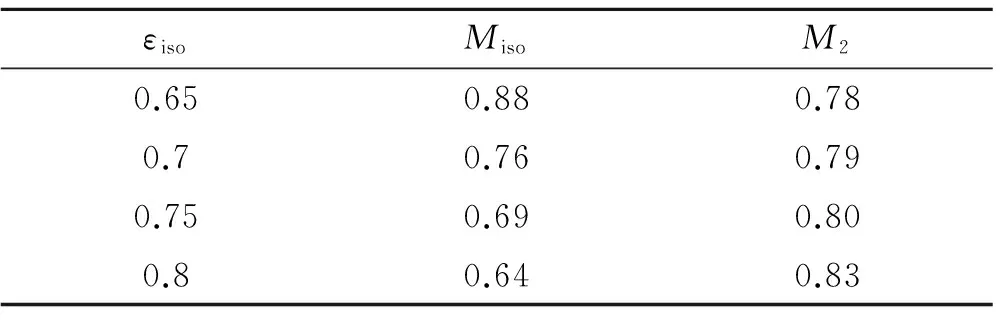
表3 二次流质量流率最大值点Table3 Parameters reaching maximum secondary flow mass flow rate ratio

4 飞行状态下主火箭总压与二次流总压的匹配性

在发动机实际工作过程中，二次流总温和总压随飞行状态的改变不断发生变化。因此，以无量纲的二次流与主火箭总压之比pr=pt,2/pt,1为变量，研究了主火箭总压与二次流总压的匹配性。针对固定的发动机结构参数(取εiso=0.7)，图6给出了不同飞行马赫数M0及总压比pr所对应的隔离段通道马赫数Miso。

如图6中虚线所示，对于任一飞行马赫数，均存在达到最大隔离段气流马赫数的主火箭总压临界值，这与地面静止状态下主火箭总压与隔离段通道面积的匹配性研究所得到的结果一致。当主火箭总压小于临界临界值时(对应于图6中虚线上方区域)，由于引射能力下降，导致隔离段气流马赫数降低；当主火箭总压大于临界值时，由于一次流需要足够的膨胀，以达到与二次流的“等压”，使二次流的等压面面积不断减小，并引起二次流在等压面达到壅塞，从而引起二次流流量减小、隔离段气流马赫数降低。

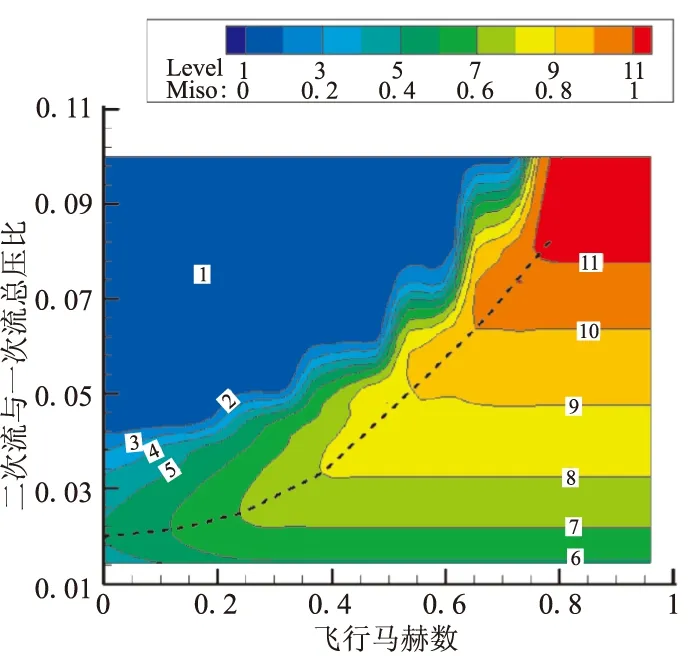
图6 隔离段马赫数Fig.6 Mach number in isolator

由图6中等值线的疏密程度可看出，在低飞行马赫数下，隔离段气流马赫数对主火箭总压的敏感性较低，而高飞行马赫数条件下的敏感性较高。因此，在低速条件下，为了满足发动机大推力、高加速的工作要求，可适当增加主火箭的总压，由此引起的空气引射量下降相对较少。

由图6可看出，当飞行马赫数较低时(约对应于M0<0.7)，过高的总压比(即主火箭总压相对较低)所对应的隔离段通道内的气流马赫数接近于0，此时难以发挥主火箭的引射作用。图中存在一个分界区域(等值线密度较大的区域)，将隔离段通道内气流马赫数接近于0的主火箭引射作用不可行状态划分出来。这表明对于任意的飞行状态均存在主火箭总压下限，飞行马赫数越低，主火箭总压下限越高。当飞行马赫数较高时(M0>0.7)，较低的主火箭总压即可令隔离段内的气流状态参数达到壅塞，这相当于进气道处于临界状态。

在一定的燃烧室反压pc作用下，进气道达到临界状态的条件：

pc<βcrpt,2

(8)

式中βcr为临界压比，对于k=1.4的空气来说，βcr=0.528 3。

式(8)可进一步整理为

(9)

式中p0为当地空气静压；π为静压与总压之比；ptr为进气道总压恢复系数；M0为飞行马赫数。

对于不同的燃烧室升压比pc/p0，图7给出了M0与fM的函数关系。从图7可看出，对于任意的pc/p0均存在一个合适的飞行马赫数Mcr令fM=1。当飞行马赫数高于临界值Mcr，进气道处于超临界状态，进入发动机内的空气流量完全由飞行状态和进气道的几何结构所决定，此时冲压作用占主导地位，也即RBCC发动机工作于空气增强火箭模式。由图7可看出，Mcr∈[1.5,2.2]。文献[7]对不同飞行马赫数开展了火箭引射模态实验，空气的引射流量如图8所示。从图8可看出，当飞行马赫数达到1.5以后，空气流量迅速提高，即来流空气的冲压作用占主导，与图7中理论分析结果一致。这也在一定程度上验证了本文所用模型的合理性。

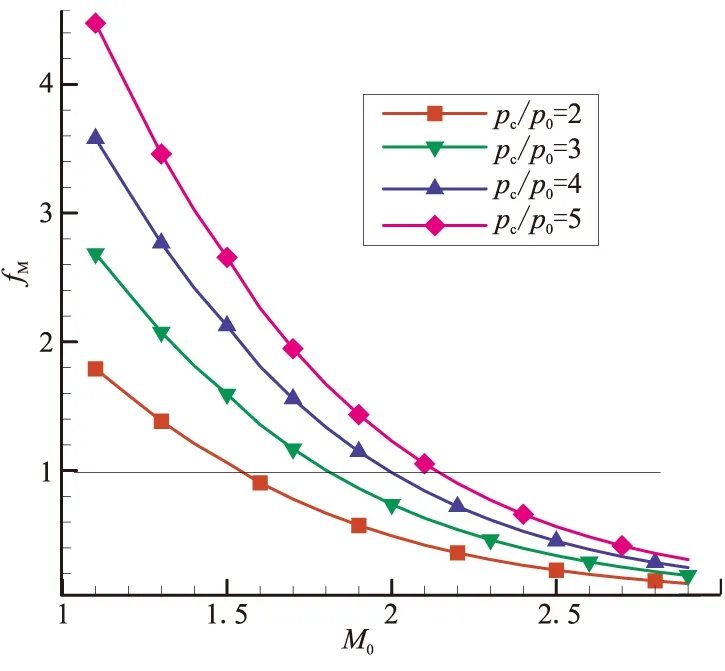
图7 M0与fM的函数关系Fig.7 M0vs fM

图8 空气引射量实验结果Fig.8 Experiment results of air mass flow rate ratio

如果飞行马赫数低于Mcr，进入发动机内的空气流量改由主火箭的引射作用所主导。但图6所示的计算结果表明，此时进气道有可能处于临界状态或者亚临界状态。因此，在火箭引射模态下，RBCC发动机的工作状态可细分为引射作用占主导地位的进气道亚临界状态和临界状态、冲压作用占主导地位的进气道超临界状态。在进气道亚临界状态下，空气流量完全由主火箭所决定；在进气道临界状态下，由于主火箭的引射作用，进气道喉部气流壅塞，空气流量由进气道的几何尺寸所限定，这一状态具有较大的马赫数跨度；在进气道超临界状态下，空气流量同样由进气道的几何尺寸决定。

5 结论

(1)为避免在较低主火箭总压条件下隔离段内二次流达到壅塞，隔离段通道面积比应不小于0.65。

(2)在地面静止状态下，随着主火箭总压增加，空气流量逐步增大，等压面上马赫数不断增加。当等压截面上的二次流马赫数约为0.8时，空气流量达到最大；等压面上形成Fabri壅塞后，进一步增加主火箭总压，反而会降低空气流量。

(3)在不同飞行马赫数下，存在决定主火箭能否发挥引射作用的一次流总压下限，存在达到最大空气引射量的一次流总压。

(4)在整个火箭引射模态下，RBCC发动机的工作状态可细分为引射作用占主导地位的进气道亚临界状态和临界状态、冲压作用占主导地位的进气道超临界状态，三者的分界马赫数分别约为0.7和1.5。

[1] Olds J R.A conceptual design for a single-stage-to-orbit space station service vehicle[R].IAF-ST-87-07,1987.

[2] 吕翔,何国强,刘佩进.RBCC飞行器爬升段轨迹设计方法[J].航空学报,2010,31(7):1331-1337.

[3] 吕翔,何国强,刘佩进,等.RBCC发动机性能分析模型改进方法研究[J].固体火箭技术,2010,33(4):387-390.

[4] 吕翔,刘佩进,何国强,等.火箭引射模态下一次火箭流量优化方法研究[J].固体火箭技术,2010,33(6):631-635.

[5] Koupriyanov M,Etele J.Theoretical investigation of the compression augmentation effect of variable area ejector[R].AIAA 2008-2619.

[6] Han S,Tomes J,Lane J.Numerical study of PSU-RBCC ejector mode operation[R].AIAA 2003-5230.

[7] 李强,刘佩进,李江,等.来流马赫数对引射火箭引射量的影响研究[R].固体火箭技术,2009,32(3):254-257.

[8] Okai Keiichi,Taguchi Hideyuki,Futamura Hisao.Exp-erimental and numerical investigations of ejector and mixing effects in a model ejector ramjet configuration[R].ISABE 2003-1230.

[9] Smith N T,Landrum D B,Moser M D.Experimental investigation of a supersonic non-axisymmetric cold flow ejector[R].AIAA 2001-3195.

[10] Lineberry D,Landrum B.Effects of multiple nozzles on asymmetric ejector performance[R].AIAA 2005-4283.

[11] Aoki Shigeki,Lee Jongsun,Masuya Goro,et al.Experime-ntal investigation of an ejector-jet[R].AIAA 2003-188.

[12] Fabri J,Paulon J.Theory and experiments on supersonic air-to-air ejectors[R].NACA TM-1410,1958.

[13] Fabri J,Siestrunck R.Supersonic air ejectors[M].New York:Advances in Applied Mechanics (Vol.V),Academic Press,1958:1-34.

[14] Chow W L,Addy A L.Interaction between primary and secondary stream of supersonic ejector systems and their performance characteristics[J].AIAA Journal,1964,2(4):686-695.

[15] Korst H H,Page R H,Childs M E.A theory for base pressures in transonic and supersonic flow[R].Univ-ersity of Illinois,1955.

[16] Porter J L,Squyers R A.An overview of ejector theory[R].AIAA 1981-1678.

[17] Pastrone Dario.An analysis of the ejector-ram-rocket engine[R].AIAA 2004-3647.

[18] 李宇飞.RBCC引射/亚燃模态热力调节机理研究[D].西安:西北工业大学,2007.

[19] 刘佩进,何国强,李宇飞.RBCC引射火箭模态二次燃烧实验[J].推进技术,2004,25(1):75-77.

[20] 王保国,刘淑艳,黄伟光.气体动力学[M].北京:北京理工大学出版社,2005.

(编辑：崔贤彬)

Operation match between primary rocket and RBCC engine during rocket ejector mode

LV Xiang, ZHENG Si-hang, HE Guo-qiang, LIU Pei-jin

(Science and Technology on Combustion, Internal Flow and Thermal-structure Laboratory, Northwestern Polytechnical University, Xi'an 710072, China)

Based on the traditional “pressure equal plane” hypothesis, ejection performance analysis model for RBCC primary rocket was established. Operation match between primary rocket and RBCC engine was investigated.The results show that: If the area ratio of isolator cross section is less than 0.65, flow choke will appear in isolator under lower total pressure of primary rocket, limiting further improvement of air mass flow.For ground static condition, the air mass flow increases with the increase total pressure of primary rocket. If fabric choke appears,further increasing total pressure of primary rocket will cause descending of air mass flow.During rocket ejector mode, the operation of RBCC engine can be divided into 3 different states, inlet sub-critical state dominated by ejecting effect, inlet critical state dominated by ejecting effect, inlet super-critical state dominated by ram effect, while the critical Mach number for these states are 0.7 and 1.5 respectively.

rocket based combined cycle;hypersonic vehicle;rocket ejector mode;primary rocket; isolator

2014-04-07；

：2014-06-08。

吕翔(1979—)，男，副教授，研究方向为发动机总体设计。E-mail:lvxiang@nwpu.edu.cn

V430

A

1006-2793(2015)02-0179-06

10.7673/j.issn.1006-2793.2015.02.006