基于A*OMP算法及其改进算法的宽带雷达信号稀疏分解

葛 明，钱 玲

(南京理工大学，南京 210000)



基于A*OMP算法及其改进算法的宽带雷达信号稀疏分解

葛 明，钱 玲

(南京理工大学，南京 210000)

传统稀疏分解算法正交匹配追踪(OMP)算法里采用内积最大值来寻找最优原子，该方法容易陷入局部最优，为了弥补这一缺点，采用了新的算法：A*OMP算法，该算法使用A*搜索(即最佳优先搜索技术)寻找最优原子，该搜索方式寻找的最优原子具有全局最优性。实验表明相比传统OMP算法而言，该算法有效地提高了信号的重构精度。

稀疏分解；正交匹配追踪算法；雷达信号

0 引 言

一直以来，奈奎斯特采样定理一直是信号采样、存储、传输领域所采用的主要方法，它要求采样频率必须大于或等于信号中最高频率的2倍，然而面对快速发展的信息化社会，该采样理论已经无法满足社会的需要。因此，近年来出现了一种全新的信号采集理论：压缩感知(CS)理论。该理论指出：若信号在某个变换域是稀疏的(稀疏性)或可压缩的，则可以设计一个与稀疏变换基不相关的测量矩阵，将变换所得的信号从高维空间投影到低维空间上，得到一组测量值，最后通过求解优化问题，将低维的测量值还原成高维的原始信号，实现信号的近似或准确重构。该理论的提出，使得能够以远低于传统采样定理所需的采样频率对信号进行采样。

1 压缩感知基本原理

压缩感知理论主要由信号的稀疏分解、测量矩阵的设计、信号重构这三大核心内容组成。

1.1 信号的稀疏分解

假设一个具有稀疏性的长度为N的一维离散实值信号f(f∈RN)，可以用变换域θ中的一组正交基ϑi(i=1,2,…N)表示，则信号可以表示[1]为：

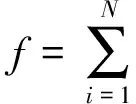
(1)

式中:β为稀疏系数，如果β中只含有K个非零值(K≪N)，则可认为信号f是K稀疏的。

1.2 测量矩阵的设计

在对信号进行稀疏表示之后，用一组与稀疏变换基不相关的测量矩阵Φ对原始信号进行投影，将信号从高维空间投影到低维空间上，则表达式为：

y=Φβ

(2)

该表达式也可以理解为：

y=Φβ=ΦθTf=Θf

(3)

式中:Θ=ΦθT，Φ为M×N矩阵(M≪N)。

由于式(2)中方程的个数M远远小于未知数的个数N，所以方程无解。但若β是K稀疏的，并且β中的非零系数的位置是已知的，则当M≥K时，该问题就能够得到解决，此时只需要式(3)中的矩阵Θ满足有限等距性质(简称RIP)，即对于任意K稀疏向量u，ε∈(0,1)满足如下不等式：

(4)

此时就能从M个测量值中还原出K个非零系数。

1.3 信号的重构

当原始信号f是可压缩的，感知矩阵Θ满足RIP准则时，就能够求出式(2)中的稀疏向量β，最后将β带入式(1)中求出原始信号f，实现了从M维的测量值y中重构出原始信号。对于β的求解可以通过求解最小l0范数问题：

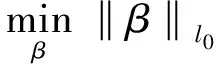
(5)

然而在求解式(5)的过程中发现，该式的求解极其复杂，而且还是个无解难题(NP)问题，所以对于求解最小l0范数问题，可以用能够产生相同解但是更为方便的最小l1范数的求解来代替，最小l1范数问题的求解如下所示：

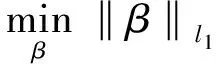
(6)

当采样点数(即独立同分布的高斯测量值的个数)满足M≥cKlg(N/K)时，就能够以很大概率重构出K稀疏向量，此时最小l1范数求解问题就变成了一个凸优化问题，该问题可以转化为求解线性规划的问题[2-4]。

2 A*OMP算法

A*OMP(即A*正交匹配追踪)算法是一种新的采用最佳优先搜索方式的半贪婪算法。该算法本质上是将A*算法与OMP[5]算法相结合的算法[6]，算法中包含了A*搜索[7-8]：一种最佳优先搜索技术,利用最佳优先搜索可以评估多条路径。

A*算法是一种迭代树形搜索算法。在每次迭代中，当前最优的路径和它所有的子集将会被添加到搜索树中，当最优路径被发现是完整的时候搜索中止。

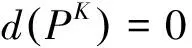
d(Pl)≥g(Pl)-g(Pl∪zK-l),∀zK-l

(7)

式中:d(Pl)大于或等于路径Pl产生的任何一个扩展路径所对应评价函数的衰减。

因此定义代价函数：

F(Pl)=g(Pl)-d(Pl).

(8)

3 使用A*算法搜索最匹配的原子

A*搜索从候选子集的单一元素开始，执行一个多路径搜索，在所有可能的含有K个原子的子集中选取最好的一个。将采用3个主要步骤来讨论A*OMP：初始化搜索树，扩展已选择的部分路径和选择最优路径。

3.1 初始化搜索树

A*搜索将搜索树的所有可能的路径长度初始化为1。由于每次迭代会在一条已选择部分的路径中添加多个子集，因此开始搜索时尽可能用很少的路径，为此限制了初始化搜索子集I(I≪K)。

3.2 扩大已选择的部分路径

在典型的A*搜索中,在每次迭代中所有最有前途的路径的子集都会被添加到搜索树中。这将产生大量的可能的子集，导致太多的搜索路径，为了限制这些,将采用如下3种修剪策略。

3.2.1 每条扩展路径的修剪

在设置A*搜索参数的时候，需要限制每个节点的扩展个数B,因此在每一次A*OMP迭代中,仅通过B子集来扩大搜索树，B子集与残留选择的路径有着内积绝对值最大值。这样可以大大减少搜索路径。

3.2.2 树尺寸的修剪

为了进一步减少内存需求,限制树中搜索路径的最大数量P,当超过这个限制,最坏的路径(即以最大的成本)从树中删除,直到P路径仍然保留。

3.2.3 等效路径的修剪

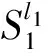
3.3 选择最好的路径

最小的残差误差是衡量最好路径的标准，因此，对于一条长度为l的路径Sl来说，评价函数可以写成如下形式：

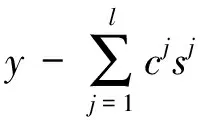
(9)

辅助函数对于评估长度不等的多条路径是极其重要的。下面利用关于残差的不同假设提出3种不同的辅助函数[5]。

3.3.1 加性代价模型

加性代价模型假定表示的K个向量的平均贡献等同于‖y‖2，则一个向量的平均贡献为δe=‖y‖2/K。一条长度为l的部分路径里未开放的K-l节点预计将减少‖r‖2，即(K-l)δe。结合式(7),辅助函数应该满足：

(10)

因此定义了加性辅助函数：

(11)

式中:β为一个大于1的常数。

最后获得了代价函数：

(12)

式中:β为正则化常数,如果它是比较大的数,则越短的路径越有利,这会使搜索过程中扩展更多的候选人,当它变得更小时,搜索就喜欢更长的路径。

3.3.2 自适应乘性代价模型

辅助函数还可以通过修改未开放节点的期望平均贡献自适应地被选择：

(13)

然后,自适应辅助函数应该满足：

(14)

在这种情况下,结合β>1最终获得自适应辅助函数：

(15)

自适应代价函数可以写成如下形式：

(16)

3.3.3 乘性代价模型

与加性辅助函数相比,乘法代价模型路径采用权重函数。这里假设每个节点减少‖r‖2，根据定比α，乘法代价函数被定义为：

(17)

在这里α应该选择在0和1之间，α的作用非常接近加性代价函数β。

3.4 A*OMP算法流程

为了全面展示该算法，算法的伪代码如下所示：

初始化：

T←∅

fori←1toIdo%将初始化路径长度设置为1

endfor

Ci=‖y‖2,Li=0,∀i=I+1,I+2,…,P

best_path←1

whileLbest_path≠Kdo

T←Sbest_path

fori←1toBdo%对每一条扩展路径进行修剪

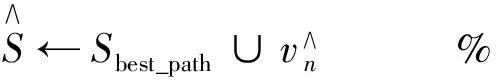
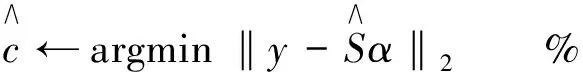
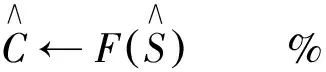
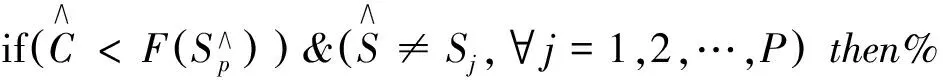
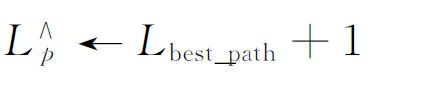
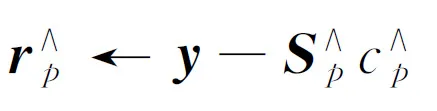
endif

endfor

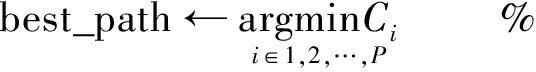
endwhile

returnSbest_path,cbest_path

3.5 算法的改进

在A*OMP算法里，通过使用代价函数，将迭代之后的扩展路径分别与迭代之前的最优路径进行对比，通过计算路径的代价，选择代价最小的作为当前最优路径，以达到更新最优路径的目的。而在使用代价函数的过程中又可以根据不同的情况选择不同的辅助函数。

而在A*OMP的改进算法里，在更新最优路径的过程中不使用辅助函数，直接将扩展节点的残差作为路径代价函数与迭代之前的最优路径的代价进行对比。这是因为最小残差误差是衡量最好路径的标准，残差越小，表明路径的代价越小，该路径就越优，因此可以直接将扩展节点的残差作为路径代价函数与迭代之前的最优路径的代价进行对比。如果残差小于最优路径，则更新当前最优路径。经过改进之后的算法将大大提高信号稀疏分解的重构精度和运行效率。

4 仿真结果与分析

本文使用频带宽度B=80 MHz,脉冲宽度T=0.5 μs、采样频率Fs=160 MHz的宽带雷达信号，对其进行稀疏分解。由于Gabor字典对稀疏信号具有普遍适用性，因此构造Gabor字典，选取字典里的基函数作为稀疏基，分别采用OMP算法和A*OMP算法以及其改进算法将信号进行稀疏分解，其仿真结果如图1～图3所示。

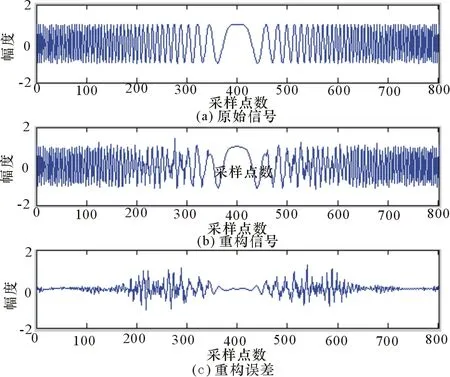
图1 使用OMP算法对信号的稀疏分解

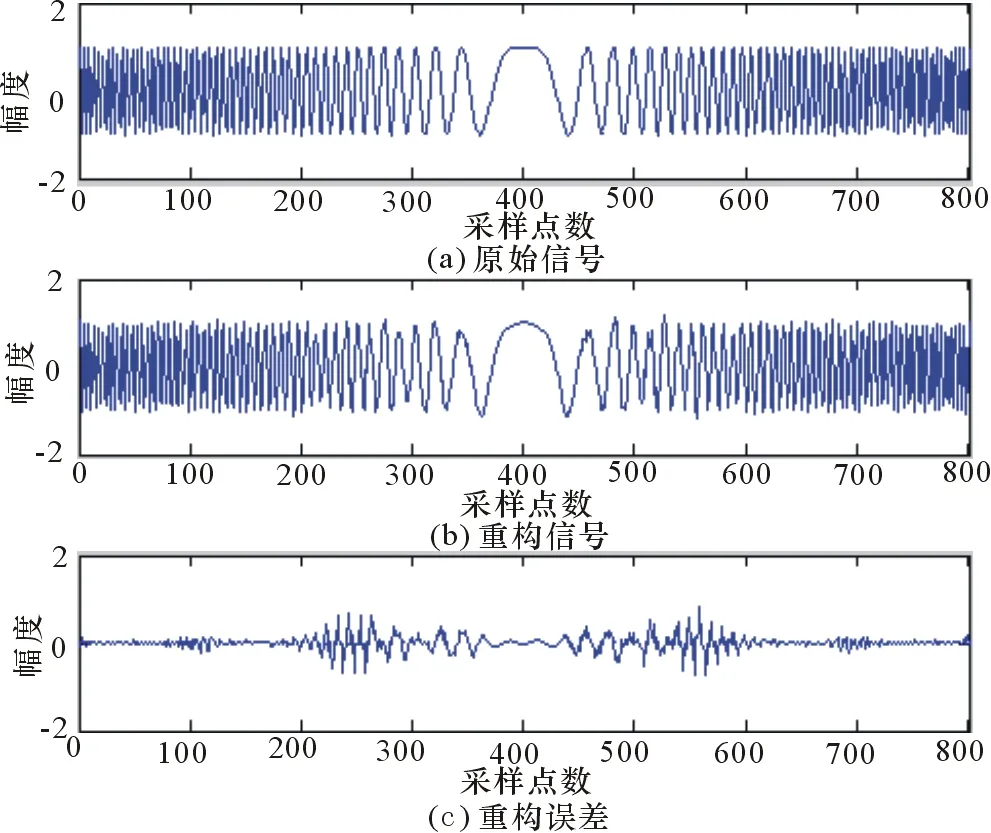
图2 使用A*OMP算法对信号的稀疏分解

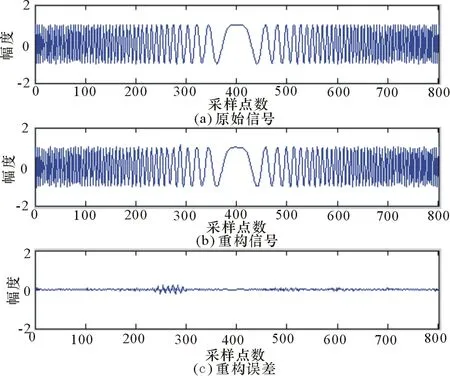
图3 使用A*OMP改进算法对信号的稀疏分解

为了进一步显示A*OMP及其改进算法的优越性，表1列出了该算法与OMP算法在相同条件下的信噪比、相对误差、匹配度以及重构运行时间的对比。

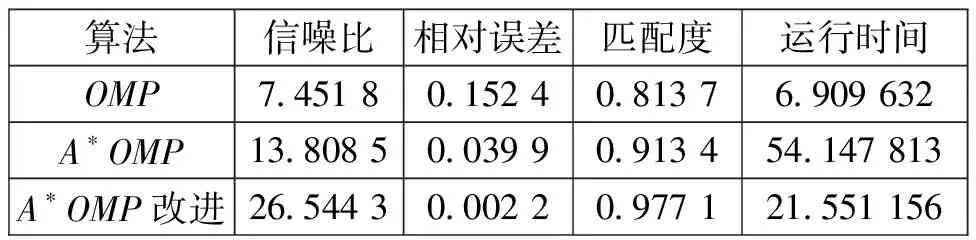
表1 信号稀疏分解的相对速度与重建质量对比

通过仿真结果可以看出，由于A*OMP算法采用的是多路径搜索，相比OMP算法的单路径搜索而言，它的运行时间要长于OMP算法的运行时间；然而在重构精度方面A*OMP算法及其改进算法要高于OMP算法，而且A*OMP算法特别是它的改进算法在运行效率方面与OMP算法相差并不大。因此总体而言，A*OMP算法要优于OMP算法。

5 结束语

本文主要介绍了与OMP算法相比，A*OMP算法及其改进算法对信号的稀疏分解具有能够大大提高重构精度的优点。OMP算法里采用内积最大值来寻找最优原子，该方法容易陷入局部最优。在用了半贪婪的A*OMP算法后，使得这种不准确的选择有了缓冲的余地。A*OMP算法通过使用A*搜索方式，使得寻找的最优原子具有全局最优性，因此在重构精度方面，A*OMP算法要优于OMP算法。目前对信号的稀疏分解仍然是研究的热点，在研究过程中根据各自不同的需求，有时候以牺牲精度来提高运算效率，有时候以牺牲运算效率来提高精度，然而这都是需要人们进行改进克服的，如何能够既提高运算效率又提高信号的重构精度仍然是人们研究的重点。

[1] Justin Romberg.Compressive sensing by random convolution[J].SIAM Journal on Imaging Sciences,2009,2(4)：1098-1128.

[2] Elad M.Optimized projections for compressed sensing[J].IEEE Transactions on Signal Processing,2007,52(12):5695-5702.

[3] Candes E J,Tao.Near optimal signal recovery from random projection:Universal encoding strategies[J].IEEE Transactions on Information Theory,2006,52(12):5406-5425.

[4] Dechter R,Pearl J.Generalized best-first search strategies and the optimality of A*[J].ACM,1985(32)：505- 536.

[5] Tropp J,Gilbert A.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on information theory,2007,53(12):4655- 4665.

[6] Nazim Burak,Karahanoglua,Hakan Erdogana.A*Orthogonal matching pursuit:best-first search for compressed sensing signal recovery,Digital Signal Processing[J],2012,22(4):1051-2004.

[7] Koenig S,Likhachev M,Liu Y,Furcy D.Incremental heuristic search in AI[J].AI Magzine,2004(25)：99- 112.

[8] 赵慧民，倪霄.压缩感知的冗余字典及其迭代阀值实现算法[J].电路与系统学报,2013(1):59-64.

[9] Jelinek F.Statistical Methods for Speech Recognition[M].Cambridge,MA,USA:MIT Press,1998.

[10]Hart P E,Nilsson N J,Raphael B.A formal basis for the heuristic determination of minimum cost paths[J].IEEE Transactions on Systems Cybernetics,1968,SS-(2):100-107.

Sparse Decomposition of Broadband Radar Signals Based on A*OMP Algorithm and Its Improved Algorithm

GE Ming，QIAN Ling

(Nanjing University of Science &Technology,Nanjing 210000,China)

In the traditional sparse decomposition algorithm——orthognal matching pursuit (OMP) algorithm,maximum inner product is used to find the optimal atom.The method is easy to fall into local optimization,in order to make up the shortcoming,a new algorithm is proposed in this paper:A*OMP algorithm,the algorithm uses A*search (the best first search technology) to find the optimal atom,the optimal atom searched by using the search way has global optimality.Experiments show that the algorithm effectively improves the reconstruction accuracy of signal compared with the traditional OMP algorithms.

sparse decomposition;orthogonal matching pursuit algorithm;radar signal

2014-08-21

TN971.1

A

CN32-1413(2015)01-0065-05

10.16426/j.cnki.jcdzdk.2015.01.016