基于悬臂梁法和面元法耦合的桨叶应力分布预报＊

叶礼裕 王 超 孙 帅 孙文林

（哈尔滨工程大学船舶工程学院 哈尔滨 150001）

0 引 言

随着现代舰船逐步向大型化、高速化发展，以及大功率主机的应用，引起螺旋桨桨叶表面负荷增大；由于减振降噪方面有特殊的优势，大侧斜螺旋桨在船舶领域得到广泛的应用［1］，但特殊的几何外形使其强度问题较为突出.另外，为了使螺旋桨实际应用中更加节能化和环保化，设计桨应当符合轻量化的要求.因此，开展螺旋桨强度的研究不仅在于桨叶强度符合规范要求，更应当能够准确地预报桨叶应力的分布.

目前，螺旋桨桨叶应力的预报通常采用有限元法和模型试验［2］.对于有限元法，开展较多的是采用CFD计算和有限元分析软件结合的方法预报桨叶应力分布［3－5］，也有学者基于面元法和有限元法耦合的方法预报桨叶应力分布［6］.在模型试验方面，Boswell［7］对大侧斜螺旋桨叶片进行了静态应力测量试验；赵波［8］开展了大侧斜螺旋桨的静态应力试验和动态应力试验，并与理论计算结果进行对比；杨向晖等［9］通过在大侧斜桨模表面粘贴应变片的方法研究不同工况下的桨叶应变和应力分布.有限元法能够较为准确预报螺旋桨桨叶应力分析，但是需要复杂的模型建立、网格划分过程，不利于开展螺旋桨的设计.模型试验方法成本较高、实验难度大且需要花费大量时间.螺旋桨运转时主要受到周向力、轴向力、离心力，以及偶然外力作用，从而产生弯曲、转矩和拉伸变形，可将桨叶简化为变截面扭曲的悬臂梁［10］.悬臂梁法也是一种比较方便且可行的桨叶应力预报方法.以往学者开展悬臂梁预报螺旋桨应力，因螺旋桨几何外形复杂且横截面为非对称的，计算截面所受弯矩、离心力，以及面积、抗弯模量等的过程中运用了一些经验公式，造成只能预报桨叶有限个点的应力或者应力预报结果，比较保守.

为准确预报桨叶各半径切面所受的弯矩和离心力，将悬臂梁法理论中的由螺旋桨推力、旋转阻力产生的弯矩、离心力及其产生的弯矩的积分计算公式进行离散处理.桨叶切面的形心和惯性矩可借助于工程力学中截面静矩和惯性矩等计算公式来求解，以准确求解桨叶各半径切面上各个点的抗弯剖面模数.本文采用FORTRAN语言编译悬臂梁法桨叶应力预报程序，将其与螺旋桨的定常面元法性能预报程序对接.以无侧斜桨和大侧斜螺旋桨为例，通过本文计算结果和有限元计算结果对比分析来验证本文所提方法的有效性.

1 悬臂梁离散方法

悬臂梁法预报螺旋桨强度是将螺旋桨叶梢视为自由端，而叶根固定于桨毂的一根变截面的悬臂梁，一般按正车最大航速工况预报螺旋桨静载荷，将作用在螺旋桨上的外力载荷视为不变.以平切面作为校核面，该校核面为垂直于桨叶参考线的面且与桨叶相交所截的平面，对大侧斜桨有更好的适用性［11］.

桨叶切面各点抗弯弹性模量计算过程如下：首先，对该切面进行分割，计算出其面积和静矩，进而求出该剖面的形心坐标；然后，计算出该剖面的惯性矩；最后，由该剖面的形心坐标和惯性矩，可求处其各点的抗弯弹性模量.具体的切面形心、静矩、惯性矩和抗弯弹性模量求解方法可参考文献［12］.

离散法可准确地计算桨叶各半径切面的弯矩.根据离散法原理，需对求解的螺旋桨几何模型进行分割.为此，将桨叶沿展向分割成有限个区域，半径r处取一叶元体，厚度为dr.为更好对接面元法预报程序，悬臂梁法的桨叶展向划分方式与面元法相同，即采用余弦分割，节点为

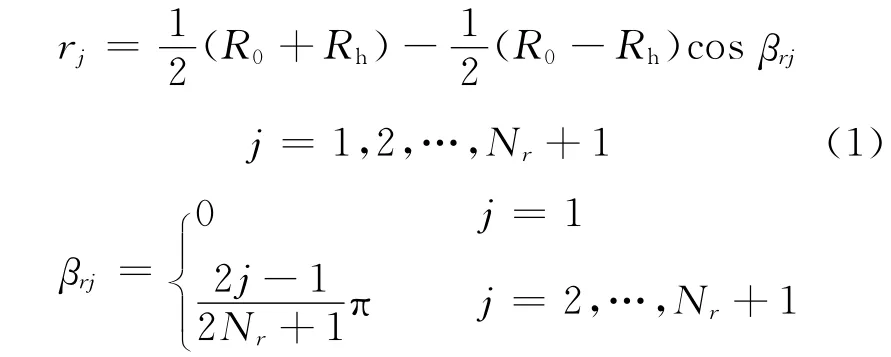
1.1 推力和旋转阻力引起的弯矩积分公式离散方法

对于常规螺旋桨，推力和旋转阻力是产生弯矩的主要成分.设该叶元体所受的推力为dT和旋转阻力dF，则桨叶推力和旋转阻力对半径处的弯矩分布为

为获得上式的数值解，将该式离散处理，沿展向分割成Nr份，则

为计算推力和旋转阻力产生的弯矩，必须计算出ΔTj和ΔFj大小，而ΔTj和ΔFj可通过面元法计算得到.面元法计算螺旋桨总的推力和转矩的离散公式为［13－14］

面元法是基于势流理论的分析方法，计算中没有考虑流体粘性的影响.为使结果更符合实际情况，计算水动力性能时，采用表面摩擦阻力的方法近似计入粘性的影响，用以下公式求解推力和扭矩的粘性修正量.

只要对面元法计算螺旋桨推力和扭矩的离散公式稍加处理，即可用于求解每个叶元体的推力和旋转阻力，即

1.2 离心力及其产生的弯矩积分公式离散方法

螺旋桨高速运转时，桨叶各径向剖面将受到离心力的作用.离心力引起的弯矩相对于推力和旋转阻力要小，但有侧斜和纵倾的螺旋桨由于离心力作用线已不是径向剖面几何中心的连线，此时产生的离心力弯矩较大.

假设螺旋桨的转速为n（r／s），材料的重量密度为γ（10kN／m3），计算半径处的切面面积为S（m2），重力加速度为g（9.8m／s2），则取一小微元dr，它对半径rP处的离心力为

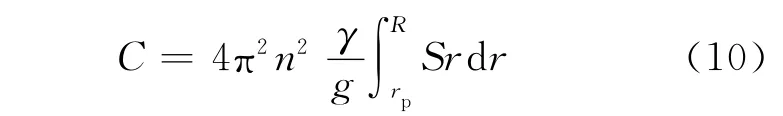
与推力和旋转阻力产生弯矩数值计算方法类似，将上述进行离散处理，得到

式中：Sj为切面的面积.

对于有纵倾的螺旋桨，将因桨叶纵倾产生离心力弯矩MC.假设在不同半径处桨叶纵倾分布为h（r），下式纵倾引起的桨叶rP处切面弯矩MC及其离散结果

对于有侧斜的螺旋桨，将因桨叶侧斜引起离心弯矩MS.通常，螺旋桨侧斜的方向是与其旋转方向相反的.因此，侧斜引起的离心力弯矩MS与纵倾引起的弯矩MF的方向相反.假设各半径侧斜分布为p（r），则侧斜引起的桨叶rp处切面弯矩MC及其离散结果为

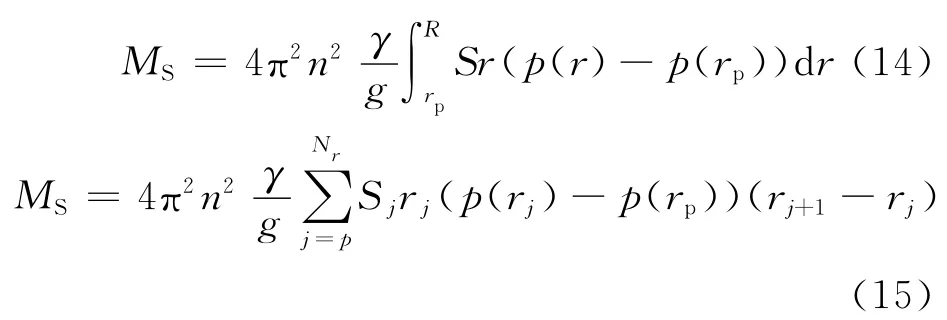
1.3 切面上各点应力求解

针对半径rp处承受的弯矩情况进行分析，见图1.将推力、旋转阻力和离心力引起的弯矩沿ξ－ξ轴和η－η轴方向分解，可以得到合成弯矩.

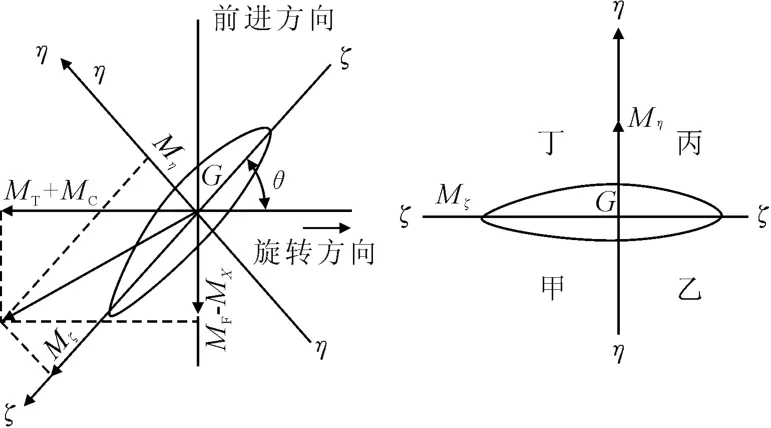
图1 桨叶剖面承受弯矩情况

校核切面的面积及切面上任何一点的抗弯剖面模数的求解方法已在以上作简要介绍.假设P（ξ，η）为切面上的一点，以Wξ（η）和Wη（ξ）分别表示P点对于ξ－ξ轴和η－η轴抗弯截面模量.那么，合成弯矩Mξ和Mη在P点处的应力可表示为：

若P（ξ，η）点所在校核切面的面积为S，则离心力C在P点产生的应力为

综述所述，合成弯矩和离心力所产生的总应力为

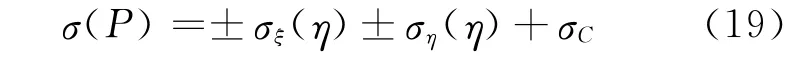
式中：σξ（η），ση（η）正负号取值需要根据具体情况而定，即ξ－ξ轴和η－η轴把校核剖面分割为4个区域，表1给出了每个区域受力状态相同.若为拉应力，则取正值.反之，取负值.

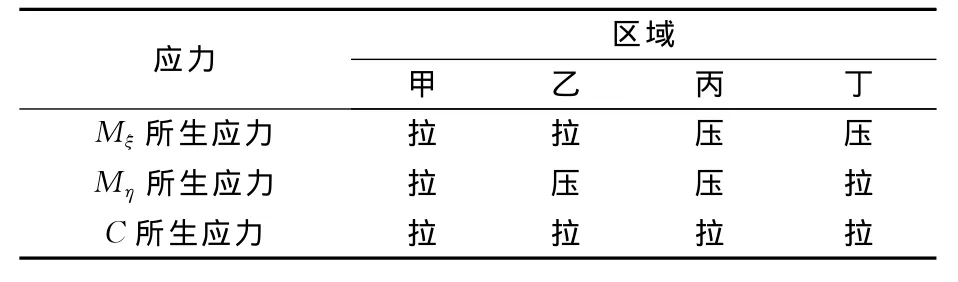
表1 桨叶剖面各区域的应力性质

2 算例分析

根据以上介绍的悬臂梁离散方法，笔者编译了悬臂梁法预报程序，并与定常面元法水动力性能预报程序进行对接，以便更好地把螺旋桨水动力性能预报传入到悬臂梁法程序计算中.程序运行计算后，可将桨叶的应力预报结果传入到Tecplot软件中进行后处理，得到桨叶应力分布云图.为了证明本文方法的可行性和有效性，将本文方法与有限元软件的桨叶应力的预报结果进行比较.

这里需要强调的是，一般情况下，任意一点的主单元体的应力状态是三向的应力.悬臂梁法是以最大拉压应力σ1为校核条件的，将其他2项应力σ2和σ3忽略不计，而有限元法计算的以von Mises应力（等效应力）σε为校核条件的，见文献［15］，σε计算方法见式（20）.根据螺旋桨的受力情况可知，桨叶上任意一点的最大拉压应力σ1远大于其他2项应力σ2和σ3.因此，桨叶任意一点的最大拉压应力σ1的绝对值与von Mises应力σs的大小相差不大.

本文选了2种类型的螺旋桨进行算例分析，包括无纵倾无侧斜的P4119、P4381桨，以及某大侧斜调距桨.

2.1 P4119桨和P4381桨的模型算例分析

对于无纵倾无侧斜桨的算例，本文选用22nd ITTC Propulsion Committee提供的P4119桨和P4381桨为算例，其几何参数见表2.

表2 P4119桨和P4381的主要参数

为了验证本文方法预报螺旋桨强度的准确性，将本文的应力预报结果与文献［16］进行比较.预报P4119桨的应力分布的工况为：进速系数0.833，转速600r／min.在该工况下.本文面元法程序和文献［16］预报的P4119桨水动力性能见表3，可见2种的误差较小.

表3 P4119桨的推力和转矩系数对比

图2为本文方法预报DTRC4119桨的叶背和叶面的应力分布.文献［16］是采用有限元计算软件计算DTRC4119桨桨叶应力分布，预报结果见图3.由图2～3可知，本文计算的桨叶的应力分布趋势与文献［16］计算结果类似.本文方法预报桨叶最大拉应力为，而文献［16］预报最大von Mises应力为，两者的最大应力预报结果偏差较小.另外，注意到文献［16］提到其最大应力发生在桨叶叶根弦向中部处，而本文预报结果最大应力也是发生在叶根弦向中部处.

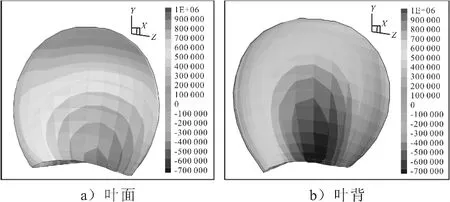
图2 本文方法预报的P4119桨桨叶应力分布

图3 文献［16］预报P4119桨桨叶应力分布

P4381桨的桨叶应力计算工况为进速2.711 45m／s、转速600r／min.P4381桨的有限元软件应力预报步骤如下：首先，在ICEM软件中建立P4381桨的几何模型并对其划分网格，导入到Fluent软件中进行水动力计算；将P4381桨的几何模型导入到ANSYS结构力学模块中进行结构网格划分，将P4381桨的水动力载荷传入到调距桨该桨的有限元模型中，计算出P4381桨叶面和叶背的应力分布.

在计算工况下，本文的定常面元法程序和CFD方法预报得到的该桨推力系数和转矩系数见表4，2种方法得到的该桨推力系数和转矩系数误差较小.

表4 P4381桨的推力和扭矩系数对比

运行悬臂梁法预报程序，得到了P4381桨的叶背和叶面的应力分布情况，见图4.有限元法预报P4381桨的叶背和叶面的应力分布见图5.从叶背应力预报结果分析，本文方法和有限元法预报的P4381桨叶背的分布趋势基本是一致的；本文方法预报叶背最大压应力为3.21MPa，而有限元法预报叶背最大von Mises应力为3.61MPa，2种方法计算得到叶背最大应力值相近且均是发生于叶根弦向中部处.从叶面应力预报结果分析，本文方法和有限元法预报的P4381桨叶面的分布趋势有一定的差别，但是叶根处的分布趋势比较相近；本文方法预报叶面最大拉应力为3.16 MPa，而有限元法预报叶面最大von Mises应力为3.61MPa，2种方法计算得到叶面最大应力值相近且均是发生于叶根弦向中部处.

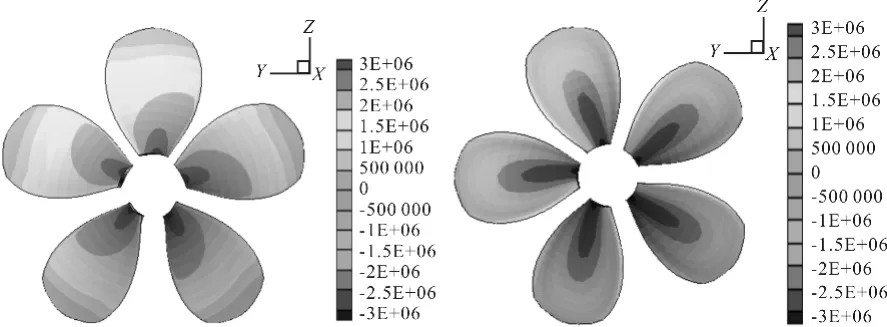
图4 本文方法预报P4381桨桨叶应力分布

图5 有限元法预报P4381桨桨叶应力分布

综上所述，本文方法可用于预报常规桨的应力分布趋势，能够准确预报常规桨的最大应力值及其发生的位置.但是，在预报常规桨叶面的外半径处的应力分布有所缺陷，主要原因是叶面外半径处叶切面比较平坦，导致同一半径处的叶切面处的应力值趋向相同.

2.2 大侧斜桨算例分析

本文大侧斜螺旋的计算模型选的是某大侧斜调距桨，主要参数见表5.

表5 大侧斜桨的主要参数

该桨的计算工况：进流速度为11.8m／s，转速为3.4r／s.有限元法计算该桨的步骤与P4119桨和P4381桨的模型算例一样.

从敞水性能预报的准确性分析，表6给出了计算工况下本文面元法和CFD方法计算得到的调距桨的敞水性能，两者的误差很小，即不会由于水动力性能计算结果的不同而引起悬臂梁法和有限元法预报该桨的桨叶应力分布有较大的差别.

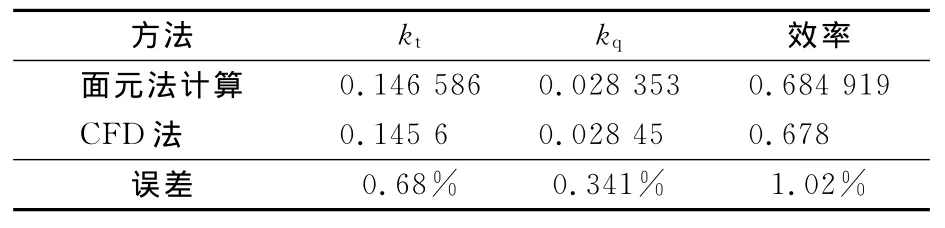
表6 大侧斜桨的敞水性能对比

本文方法预报该桨的桨叶应力分布云图见图6.由图6可知，本文方法预报的桨叶最大压应力为83.6MPa，发生于叶背中部的弦向中部处，桨叶压应力也主要集中于叶背中部弦向中部处；最大拉应力为92.7MPa，发生于叶面中部的随边处，桨叶的拉应力主要集中与桨叶中部的导边和随边处.有限元软件预报该调距桨的桨叶应力分布云图，见图7.由图7可知，有限元法预报的叶背最大von Mises应力为83.2MPa，发生于叶背中部的弦向中部靠近随边处，桨叶的拉应力也集中于此处；叶面最大von Mises应力为91.6 MPa，发生于叶面中部的弦向随边处.2种方法预报大侧斜桨叶背和叶面的最大应力大小差别小，且发生位置比较相近，验证了悬臂梁法在计算大侧斜桨桨叶应力分布的可行性和准确性.但是，2种方法预报的桨叶应力分布趋势有所差别，即悬臂梁法预报拉应力集中于叶面中部的导边和随边处，而有限元法预报拉应力只集中于叶面中部的随边处，主要原因是：由于悬臂梁法的弯矩计算原理的局限性，导致计算得到同一径向处不同弦向位置的弯矩是相同的，而有限元法计算得到同一径向处不同弦向位置的弯矩是不同的.

图6 本文方法预报的大侧斜桨桨叶的应力分布

图7 有限元法预报大侧斜桨桨叶的应力分布

4 结 论

由于螺旋桨的几何外形复杂，悬臂梁法理论螺旋桨推力、旋转阻力产生的弯矩、离心力及其产生的弯矩的积分公式很难用解析的方法求出.为准确计算出桨叶切面的弯矩和离心力，本文建立了悬臂梁离散方法用于求解桨叶切面所受弯矩和离心力的.基于FORTRAN语言编译悬臂梁法桨叶应力预报程序，并与螺旋桨定常面元法性能预报程序对接.以无纵倾无侧斜桨和大侧斜螺旋桨为例，预报桨叶应力分布，将计算结果与有限元法计算结果相比较，分析得到如下结论.

1）本文方法能较为准确的预报无纵倾无侧斜桨的叶面和叶背最大应力值，且对于该类型的桨最大应力发生于桨叶叶根的弦向中部.除了预报常规桨叶面的外半径处的应力分布有所缺陷，本文方法预报常规桨的桨叶的应力分布趋势与有限元法预报趋势是相同.

2）本文方法可较为准确预报大侧斜桨的叶面和叶背最大应力值.对于本算例的平衡式侧斜桨，最大拉应力一般发生于桨叶中部的随边处，最大压应力发生于桨叶中部的弦向中部处.悬臂梁法预报桨叶应力分布趋势有缺陷，即悬臂梁法预报螺旋桨的拉应力在叶面中部的导边和随边处有集中现象，而实际上对于该桨拉应力只集中于叶面中部的随边处.

总而言之，应用本文方法可快速得找到在计算工况下的螺旋桨桨叶最大应力大小及其发生位置，便于对螺旋桨的强度校核.虽然本文方法预报在桨叶应力分布趋势与有限元法还存在某些缺陷，但是总体上还是可行的.在后续的工作中，作者将开展将该方法的程序嵌入到螺旋桨的理论设计和优化设计过程中，以保证设计桨有足够的强度.

［1］CUMMING R A，MORGAN W B，BOSWELL R J.Highly skewed propellers［J］.SNAME Transactions，1984（1）：90：98.

［2］SØNTVEDT T.Propeller blade stresses，application of finite element methods［J］.Computers ＆ Structures，1974，4（1）：193－204.

［3］文学栋，王永生，李坚波.船用螺旋桨桨叶应力数值计算［J］.船海工程，2010，39（1）：27－30.

［4］柳章存.船用螺旋桨的数值模拟及流固分析［D］.镇江：江苏科技大学，2012.

［5］任 弘，李范春，杜 玲.流固耦合作用对螺旋桨强度影响的数值计算［J］.武汉理工大学学报：交通科学与工程版，2015，29（1）：144－147.

［6］刘竹青，陈奕宏，姚志崇.基于面元法及有限元法耦合的螺旋桨强度计算［J］.中国造船，2012，53（1）：25－30.

［7］BOSWELL R J.Static stress measurements on a highly－skewed propeller blade［R］.Naval Ship Research and Development Center Washington DC，1969.

［8］赵 波.大侧斜螺旋桨强度研究［D］.武汉：华中科技大学，2003.

［9］杨向晖，程尔升.大侧斜螺旋桨桨叶应力测试研究［J］.船海工程，2004（1）：6－9.

［10］盛振邦，刘应中.船舶原理：下册［M］.上海：上海交通大学出版社，2004.

［11］高同兵，程尔升.大侧斜螺旋桨设计中的考虑［J］.船海工程，2004（2）：1－3.

［12］杨在林.工程力学［M］.哈尔滨：哈尔滨工程大学出版社，2010.

［13］苏玉民，黄 胜.船舶螺旋桨理论［M］.哈尔滨：哈尔滨工程大学出版社，2003.

［14］杨在林，宋天舒，杨 勇.材料力学：下册［M］.哈尔滨：哈尔滨工程大学出版社，2011.

［15］KOYAMA K.Comparative calculations of propellers by surface panel method－workshop organized by 20th ITTC propulsion committee［J］.Papers of Ship Research Institute，1993，16（S）：57－66.

［16］顾铖璋，郑百林.船用螺旋桨敞水性能与桨叶应力的数值分析［J］.力学季刊，2011，32（3）：440－443.