基于FCM的扇区交通运行特征分析

董 斌 胡明华 丛 玮 王艳军

（南京航空航天大学民航学院 南京 211106）

0 引 言

随着我国航空运输业的快速发展，飞行流量迅速增加，空中交通运行环境日益复杂，全面描述扇区交通运行特征对于分析交通态势演化规律、提高管制运行安全和效率具有重要意义.扇区交通运行特征的描述依赖所使用的度量指标，一直以来，由于研究者关注的重点不同，所提出的反映运行特征的指标也各不相同.R.Christien等［1］提出定量描述航空器对之间的相互关系是反映交通运行特征的一种新方式，相关统计指标包括高度改变航空器数量、冲突航空器数量等；E.P.Buckle等［2］的观点是空域占有量是表示交通运行特征的要素之一，是对扇区内航空器拥挤程度的直接度量，统计指标包括管制飞行时间及距离、扇区边界飞行时间等；M.Prandini等［3－5］则认为描述特定交通态势的指标可以评价管制难度，航空器密度是其中的重要指标；赵嶷飞等［6－7］通过航空器速度／航向、航空器接近率、航空器间隔标准等指标描述某一时段内，给定扇区中交通的内在规律.复杂性是反映交通运行的重要特性，因此用于刻画交通、管制、认知等各类复杂性指标也是对运行特征分析的基础，G.B.Chatterji等［8］指出空域复杂性是航空器混合程度、接近程度、间隔等众多影响要素的作用结果；P.Kopardekar等［9］将动态密度定义为对管制复杂性有影响的所有要素的集合，相关指标包括航空器间隔处于0～5／5～10nmile的航空器对数量、预计冲突航空器对数量等.

实际上，扇区交通运行特征具有多维特性，仅从单一角度无法全面概括其运行特征.本文在已有研究成果基础上，筛选可客观描述扇区交通运行特征的多项指标，并基于指标的基本属性将其分为密度类指标、动态类指标以及冲突类指标.采用模糊C均值聚类算法，根据不同的指标集合分别对样本数据进行聚类分析.结合实际运行特征，依据各类中样本的数值分布特征，探寻不同类别的交通运行特征的共性和差异，从而更加全面地描述不同时刻的扇区交通运行特征.

1 指标集合

扇区交通运行特征是多维的，其中密度性特征是其中最基础的特征，体现的是扇区内航空器的聚集状态，航空器的分布是最能直观反映交通特征的指标，也一直是最重要的指标，但单一的密度性特征难以细致刻画扇区内航空器状态分布.本文将以密度性特征为基础，引入更深层次的动态性特征以及冲突性特征：动态性特征体现的是航空器状态的改变和迁移，每一次航空器的状态变化，都有可能引发扇区内交通态势的连锁反应，航空器在各个时刻的动态特征也需要充分关注；冲突性特征体现的是扇区内潜在的冲突风险，对于管制运行而言，安全是最重要的运行品质，通过度量冲突性指标也能侧面反映交通运行的安全水平，同时冲突也是管制员工作负荷的重要因素，综合考虑，冲突类指标的重要性不言而喻.与以往研究不同，本文描述的交通运行特征一直紧扣管制运行的基本属性，均能从实际运行角度找到有力的支撑，从而更加合理地反映运行问题，为实际运行提供指导.因此，从上述3个角度可以全面阐述不同时刻扇区交通运行特征.

根据指标的分类特性，结合实际数据的指标可计算性，筛选的指标及指标分类结果见表1.为了描述方便、表达清晰，对指标进行编号，后续描述均用指标编号代替指标名称.指标的计算模型参见文献［10－11］.

表1 扇区交通运行特征指标

2 模糊C均值聚类算法

本文采用聚类分析方法探寻不同时刻交通运行状态的分类特征，明确分类之间的特征差异和变化趋势，从而直观的反映不同时刻交通运行特征的异同，为进一步分析不同层级的扇区交通运行特征奠定基础.为使聚类结果更具有说服力，选用无监督机器学习算法中应用最广泛且较成功的模糊C均值聚类算法（FCM）.

FCM是一种基于划分的聚类算法，与传统的硬划分聚类分析算法不同，FCM是一种基于模糊集合的软划分聚类分析算法；FCM通过计算待分类样本与各个类别的隶属度，表达样本类属的中介性，从而建立了样本对于类别的不确定性描述，能够更客观的反映样本的分类属性.

FCM算法步骤如下.

2）初始化隶属矩阵U 令U ＝ （uni）N×I，满足约束条件uni∈ ［0，1］和 ＝1，i＝1，2，…，I.其中：N为所需分类个数.

3）根据隶属矩阵U，确定N个分类的聚类中心 C ＝ （Cn）N×1，n ＝ 1，2，…，N.式 中：Cn＝为加权指数.

5）将价值函数值J的计算结果与前一次计算结果进行比较（为方便计算若J为第一次计算结果，则默认前一次计算结果为0），判断价值函数值改变量是否小于设定停止阈值ε，若小于ε则算法终止；否则，根据对隶属矩阵U进行更新，并重复3）、4）两步，直至价值函数该变量小于停止阈值ε.

6）根据算法计算结束后的隶属矩阵U判断数据对象所属分类，xi∈Class（n），if uni＝max［u1i，u2i，…，uNi］.

根据3类指标集合，使用模糊C均值聚类算法，分别依据密度性、动态性、冲突性3类特征对多个时刻的交通状态进行聚类分析，明确各时刻所属多类特征的等级程度，有利于精确把握不同时刻下的交通运行特征.

3 实例分析

选取某区域管制中心某扇区的实际历史数据，每条数据记录包括航班时刻、经纬度信息、速度、航向等.选取08：00～09：00（早高峰），13：00～14：00（午高峰），17：00～18：00（晚高峰）3个时段，以5min为间隔选取36个时刻样本，并计算对应指标值.

设置模糊C均值聚类参数 依据专家经验加权指数m∈ ［1.5，2.5］时聚类结果较为精确，通常可取加权指数m＝2［12－13］；经多次实验验证，当停止阈值小于10－5时，聚类结果并不会发生变化，且算法效率大幅下降，因此设置停止阈值ε＝10－5，为直观对比描述扇区交通运行特征设置分类数N＝3.

为了方便描述，对样本进行编号：08：00～09：00所选取的12个样本编号依次为1～12，13：00～14：00所选取的12个样本编号依次为13～24，17：00～18：00所选取的12个样本编号依次为25～36.聚类结果见表2.表中：I类所包含的样本具有出密度性小，动态性弱，冲突性小的特征；III类所包含的样本具有密度性大，动态性强，冲突性大的特征；II类所包含的样本的各个特征处于上述两类之间，属于中等水平.

表2 聚类结果

首先分别从各类特征指标集合中选取典型指标，对比不同划分等级中的样本均值和方差，详细阐述其数值分布规律.结果见图1～3.

图1 容流比均值标准差图

图2 平飞航空器架次均值标准差图

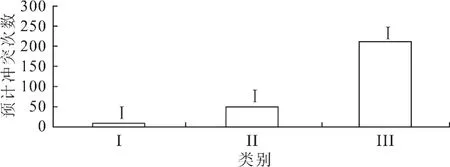
图3 预计冲突次数均值标准差图

由图3可知，按不同指标集合对样本数据分类，选取的典型指标在对应的各个类别中标准差均比较小，表明了聚类方法的可用性以及准确性；I、II、III类典型指标均值具有明显的上升趋势，说明I、II、III类样本的分布能够明显反映类别之间不同交通运行特征的差别.依据聚类结果，通过对比不同分类中样本各数值的分布特性，详细分析各类的扇区交通运行特征.

分别依据按密度类指标、动态类指标、冲突类指标聚类的结果，样本指标分布见图4～6.

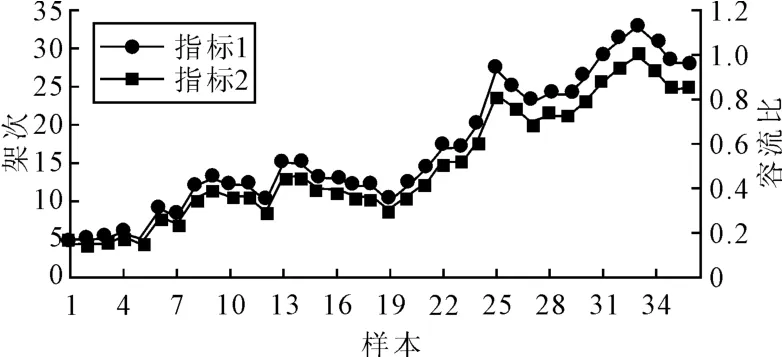
图4 样本密度类指标分布

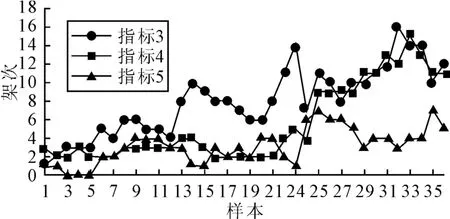
图5 样本动态类指标分布

由指标1，2的数值分布可知，I类中样本航空器数量均小于10架次，容流比均小于0.3；II类中样本航空器数量均处于12～20架次之间，容流比处于0.3～0.65之间；III类中样本航空器数量均大于22架次，容流比均大于0.75.

指标3，4，5主要体现的是样本时刻扇区内航空器的状态分布特征，由指标3的数值分布可知，I类中62.5%的样本中平飞航空器数量为2～5架次，II类中60%的样本中平飞航空器数量为6～9架次，III类中61.5%的样本中平飞航空器数量为10～13架次.说明指标3在类内会产生聚集，而不同类之间的聚集范围有明显差异，指标4，5反映出相似的性质；这表明不同类的动态状态特征之间存在较明显的差异.

指标8，9，10，11主要体现的样本时刻扇区内航空器的冲突分布特征.目前，数据来源扇区采用雷达管制，管制间隔为10km，因此间隔小于5 n mile的航空器架次对即可代表反应当前时刻的冲突风险，由图6可知，I类中几乎所有样本均不存在间隔少于5nmile的航空器架次对，II类中78.9%的样本包含至少4对间隔小于5nmile的航空器，III类中所有样本均包含至少30对间隔小于5nmile的航空器，指标9，10，11能够表现出相似的分布特性，这表明不同类的航班分布特征具有明显差异.

综上所述，指标的样本分布基本符合聚类结果，从早高峰至晚高峰，各类密度类指标虽然会出现局部波动，但整体呈现上升趋势.结合密度性特征可知，基础指标航空器数量一直稳定增加，而从早高峰至晚高峰，各类动态特征指标的总体部分基本呈递增趋势.但与密度类指标相比，动态类指标对交通运行特征具有更加细微的表征能力.例如，中午时段的航空器数量分布高于上午时段，但爬升航空器数量和下降航空器数量的数值范围基本类似；晚间时段与中午时段相比，平飞航空器数量分布范围基本重叠.总体看来，航空器的下降状态出现较少，整体变化幅度较小；而平飞和爬升状态则出现较多，整体变化幅度也更大.所以，对于管制员而言，需要重点关注晚上高峰时段内航空器的爬升状态，而对下降和平飞状态则可以投入较少的精力.可见，当航空器数量不同时，扇区的动态性运行特征也会出现相似的分布.对于日趋繁忙的管制扇区，实时掌控航空器的三维运动态势才能更好得实施管制策略，减少扇区运行的复杂性.与动态类指标相比，冲突类指标对交通运行过程中存在的潜在风险具有更直观的表征.对于日趋繁忙的管制扇区，实时掌控扇区内的潜在冲突可以更高效的实施管制策略，从而提高扇区运行的安全性.

图6 样本冲突类指标分布

4 结束语

本文提出了一种新的扇区交通运行特征分析方法.基于运行数据分析指标的分布规律，通过模糊C均值聚类方法对扇区不同运行时刻的运行特征进行聚类分析，明确所选样本时刻的分类特性，进而结合样本的数值分布分析不同时刻交通运行的多维属性.

通过对早高峰、午高峰、晚高峰等3个典型时段的指标分析，可以发现，随着时间的变化，早高峰、午高峰、晚高峰的航空器密度不断增加；当该扇区处于中等密度水平时，扇区内存在的潜在水平冲突次数处于较低水平，这不并足以使管制员过多实施改变高度的管制策略，相较于低密度时扇区的动态性，此时的管制策略主要是调整航空器的速度；当该扇区处于高密度水平时，扇区内存在的潜在冲突风险急剧增加，此时，单一的管制策略不足以缓解扇区内的冲突，因此管制员通过改变航空器速度／航向／高度多种策略缓解扇区内的冲突风险.综上所述，3类指标集合能够客观、综合地描述交通运行的不同特征，既能宏观展示交通态势的分布趋势，又能保留交通运行的各层细节，是深入挖掘交通运行的时空演化规律的基础支撑.

本文主要对描述扇区交通运行特征提供了一种新的思路，不同的聚类算法对于结果的影响尚未研究，同时如何从连续的时间序列上描述扇区交通运行特征将是下一步的研究重点.

［1］CHRISTIEN R，BENKOUAR A，CHABOUD T，et al.Air Traffic Complexity Indicators ＆ ATC Sectors Classification［EZ］.http：／／www.atmseminar.org／papers.cfm？seminar＿ID＝5，2003－06－28.

［2］EDWARD P.BUCKLEY，B.DEBARYSHE B，et al.Methods and measurements in real time air traffic control system simulation［R］.DOT／FAA／CT－83／26，Washington DC.，FAA，1983.

［3］PRANDINI M，PIRODDI L，PUECHMOREL S，et al.Toward air traffic complexity assessment in new generation air traffic management systems［J］.IEEE Trans.On Intelligent Transportation Systems，2011，99：1－10.

［4］PRANDINI M，PUTTA V，HU Jianghai.Air traffic complexity in a dvanced automated air traffic management systems［C］.Proceedings of the 9th Innovative Research Workshop and Exhibition，2010.

［5］PRANDINI M，HU Jianghai.A probabilistic approach to air traffic complexity evaluation［C］.Proceedings of the 48thIEEE Conference on Decision and Control Conference，Piscataway，New Jersey：IEEE，2009：5207－5211.

［6］ZHAO Yifei，ZHANG De，YUE Rentian，et al.Method to analyze air traffic situation based on air traffic complexity map［C］.9th USA／Europe ATM R＆D Seminar，Berlin，Germany，2011.

［7］赵嶷飞，张 德.空中交通复杂性的概念及方法研究［C］.中国航空学会航空电子与空中交通管理分会，中国航空通信导航监视及空管学术会议论文集，北京：航空工业出版社，2010：155－160.

［8］GANO B C，SRIDHAR B.Measures for air traffic controller workload prediction［C］.the 1stAIAA Aircraft，Technology，Integration，and Operations Forum.Reston，Virginia：AIAA Inc.，2011：2.C.4－1－2.C.4－9.

［9］KOPARDEKAR P，MAGYARITS S.Measurement and prediction of dynamic density［C］.Proceedings of the 5th USA／Europe Air Traffic Management R＆D Seminar，Budapest，Hungary，2003.

［10］张 晨.空中交通管理中的交通行为复杂性研究［D］.南京：南京航空航天大学，2012.

［11］丛 玮，胡明华，谢 华.空中交通复杂性指标体系精炼方法研究［J］.武汉理工大学学报：交通科学与工程版，2014，38（3）：611－614.

［12］PAL N R，BEZDEK C.On cluster validity for zhe fuzzy c－means model［J］.IEEE Trans.Fuzzy System，1995，3（3）：370－379.

［13］高新波，裴继红，谢维信.模糊C－均值聚类算法中加权指数m 的研究［J］.电子学报，2000（4）：80－83.