变刚度电液力负载模拟器自适应反步控制
2015-04-16宝仁华中科技大学机械学院FESTO气动中心湖北武汉430074
, , 宝仁, , (华中科技大学 机械学院FESTO气动中心, 湖北 武汉 430074)
引言
负载模拟器是被动式电液力伺服系统,主要用于在实验室条件下模拟被测设备工作过程中受力特性,以检验被测设备技术性能指标。海洋船拖曳系统通过钢丝绳进行吊放作业,为模拟吊放系统工作过程中所受载荷,设计一变刚度电液力负载模拟系统。如图1所示,此电液力负载模拟通过电液伺服阀驱动液压马达输出力矩,通过钢丝绳与海洋船拖曳系统连接,最终实现海洋船拖曳过程拉力变化的模拟[1]。
加载系统与拖曳系统之间的连接刚度直接影响加载系统的动态品质,对系统频宽及多余力都有较大的影响[2]。 海洋船拖曳负载模拟器以钢丝绳为力传递介质,而钢丝绳是一种柔性体,其刚度随传递力的变化而改变,并影响拖曳负载模拟器性能。反步控制基于系统数学模型,将高阶系统分解为多个低阶子系统,分别为各子系统构造虚拟控制器并给出李雅普诺夫函数,最终的控制信号由一系列虚拟控制信号递归而得,是一种处理非线性系统的有效方法[3]。自适应控制通过在线辨识系统模型参数而实时更新控制器系数,从而保证系统性能在大范围具有良好的一致性,自适应控制与反步控制结合的方法已经成功应用于多种伺服控制系统中[4,5]。

图1 变刚度负载模拟器系统方案原理
为保证变刚度负载模拟系统在8~120 kN的加载范围内系统性能具有良好的一致性,本研究通过设计间接自适应算法对系统刚度进行在线辨识,并结合反步设计法获得自适应反步控制器,最终通过仿真研究对构建的自适应反步控制器进行验证。
1 数学建模
根据电-液伺服阀流量方程、液压马达流量连续性方程及液压马达力矩平衡方程构建变刚度负载模拟系统数学模型[1,6]。
液压马达和负载力矩平衡方程:
KR(Rθm-RLθL)
(1)
液压马达流量连续性方程:
(2)
伺服阀阀口流量连续性方程:
qL=Kqxv-KcpL
(3)
钢丝绳拉力方程:
F=K(Rθm-RLθL)
(4)
式中:Tm—— 液压马达输出扭矩,N·m
pL—— 加载马达负载压力,Pa
Dm—— 加载马达排量,m3/rad
Jt—— 液压马达和负载折算到马达轴上的等效负载惯量,kg·m2
θm—— 负载模拟系统卷筒角位移,rad
Bm—— 液压马达和负载的等效粘性阻尼系数,N·m·s/rad
R—— 卷筒半径,m
RL—— 升沉绞车卷筒半径,m
θL—— 升沉绞车卷筒角位移,rad
qL—— 加载马达负载流量,m3/s
Vt—— 马达的有效容腔,m3
Ctm—— 马达总泄漏系数
βe—— 有效体积弹性模量,N/m2
Kq—— 伺服阀流量增益,m2/s
Kc—— 伺服阀流量压力系数,m5/(N·s)
xv—— 伺服阀阀芯位移,m
K—— 钢丝绳刚度,N/m
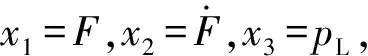
(5)

Kce=Kc+Ctm。
2 自适应反步控制器设计
自适应反步控制器原理如图 2所示,控制器主体为反步控制,通过在线辨识钢丝绳刚度更新反步控制器中参数以降低钢丝绳刚度变化对控制器性能的影响,获得系统性能大范围的一致性。
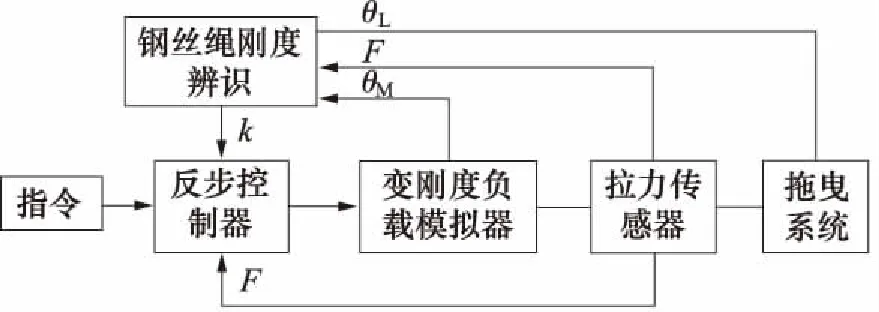
图2 变刚度负载模拟器自适应反步控制原理图
2.1 反步控制器设计
步骤1:
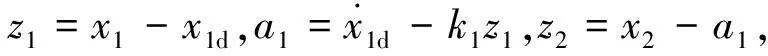
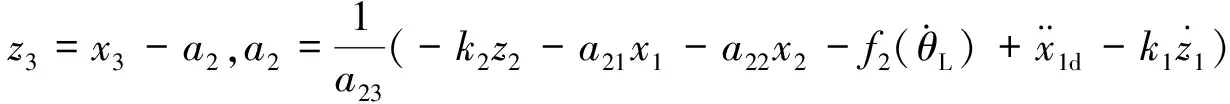
步骤2:
(7)
取控制参数为:
其中:
定义一个半正定李雅普诺夫函数:
(9)
对其求导可得:
(10)
因此,误差指数收敛。
2.2 基于最小二乘法的参数辨识
钢丝绳刚度随拖曳力变化,且可以表示为拖曳力的二次函数(K=a1F2+a2F+a3)。本研究基于最小二乘法对二次函数系数进行辨识,然后将钢丝绳刚度预估值代入(8)中,实现拖曳负载模拟器的自适应反步控制。
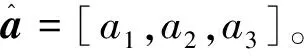
(11)
参数更新率为:
(12)
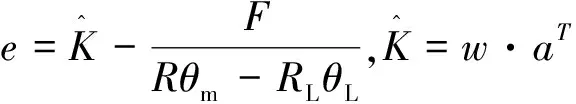
最小二乘估计可以平均测量噪声的影响,获得准确的钢丝绳刚度值,结合反步控制器可以有效抵消钢丝绳刚度变化对变刚度负载模拟系统的影响。
3 仿真研究
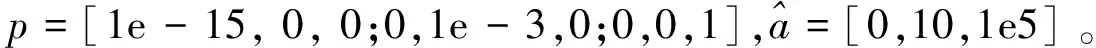
首先,将拖曳系统固定(θL=0),以考核钢丝绳刚度变化对系统特性的影响。系统对阶跃信号的响应曲线如图 3所示,由图中可以看出当输出负载力降低时,PID+前馈控制的超调量增加,调整时间增长,系统特性变差。系统对正弦信号的响应曲线如图4所示,对比图4a~图4c可知,当输出负载力减小时,PID+前馈控制的响应明显滞后,不同输出力时幅值衰减特性存在一定差异。仿真结果表明,固定参数的PID+前馈控制不能够在整个负载力工作范围内保证控制性能具有良好一致性,而自适应控制由于对钢丝绳刚度进行在线辨识并据此更新控制器参数,在整个工作范围内实现了负载力的精确模拟。

表1 变刚度负载模拟系统具体参数表

图3 变刚度负载模拟系统阶跃响应曲线
跟踪如图3所示阶跃指令时,钢丝绳二阶函数系数辨识值如图5所示,计算得到的钢丝绳刚度(K值)如图 6所示,结果表明自适应模块能够快速辨识二阶函数系数并且能够很快的跟踪钢丝绳刚度变化。
图7所示为拖曳系统跟踪幅值为0.8 rad,频率为0.1 Hz的运动时,变刚度负载模拟系统跟踪100 kN指令信号时的多余力。仿真结果表明,自适应反步控制可以有效补偿被加载系统运动产生的多余力,提高负载模拟系统性能。

图4 跟踪正弦指令的响应曲线

图5 钢丝绳刚度二阶函数系数辨识曲线
4 结论
钢丝绳刚度的变化影响负载模拟器性能,常规线性控制器难以实现其大范围精确负载力模拟。本研究采用反步法设计了基于系统数学模型的控制器,采用自适应辨识算法在线辨识钢丝绳刚度并将辨识值引入反步控制器,以保证在整个负载力模拟范围内具有良好的性能及一致性。仿真结果表明,自适应反步控制可以实现变刚度负载模拟器的高精度控制,能够保证系统性能在大范围内具有良好的一致性,且可以消除多余力多负载模拟系统精度的影响,研究结果对后期实验研究具有一定指导意义。
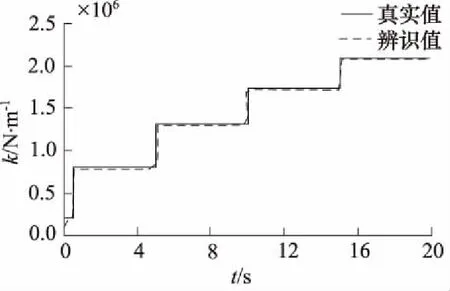
图6 钢丝绳刚度辨识值

图 7 θL=0.8 sin (0.1×2πt)时,跟踪100 kN指令信号的多余力
参考文献:
[1]杨钢,刘迎雨,杜经民,等.基于模糊PID控制器的电液负载模拟系统[J].华中科技大学学报(自然科学版),2012,40(4):59-62.
[2]裴忠才,吴盛林,苏东海,等.连接刚度对电液负载仿真台的影响[J].哈尔滨工业大学学报,1997,(5):115-117.
[3]K Khalil H.Nonlinear Systems[M].Upper Saddle River,Ner Jersey:Prentice Hall,2002.
[4]袁朝辉,袁鸣.电液系统中新型反步自适应控制器设计[J].机电工程,2013,30(7):769-773.
[5]张彪.电液负载模拟器多余力矩抑制及其反步自适应控制研究[D].哈尔滨:哈尔滨工业大学,2009.
[6]刘迎雨.拖曳负载电液伺服系统研究[D].武汉:华中科技大学,2012.
[7]Slotine J-J E,Li W.Applied Nonlinear Control[M].Michigan:Prentice Hall,1991.
