圆柱壳开孔接管补强结构有限元分析

龚宝龙 杨雪华 徐兴华

（中核苏阀科技实业股份有限公司）

0 引言

在石油、能源、核工业等行业中，广泛存在着圆柱壳形压力容器，由于工艺或结构上的需要，壳体上经常需要进行开孔并与接管进行焊接。在壳体与接管的焊接处，其连续性受到影响，容易产生明显的应力集中，导致该处往往成为整个壳体中较为薄弱的环节。适当地设计接管与壳体的结构形式，对焊接处进行补强，以提高容器壁面强度，可以提高设备的安全性。

本文选取典型的圆柱壳开孔接管补强结构，采用三维线弹性有限元数值分析手段进行应力分析，得到其应力分布规律。对应力集中系数进行研究，并通过ASME经验公式与有限元分析结果进行对比，验证数值模拟结果的准确性，为类似结构的压力容器的分析设计提供基础参考。

1 材料特性与数值模型

1.1 材料模型和特性

圆柱壳体材料Q345R和接管材料Q345的化学性能分别参考 GB 713—2008[1]和 GB/T 1591—2008[2]；机械性能参考GB 150—2011[3]，见表1。两种材料的应变强度特性可由ASMEⅧ-2附录3.D中的方程3.D.1计算获得[4]，应力-应变曲线见图1。

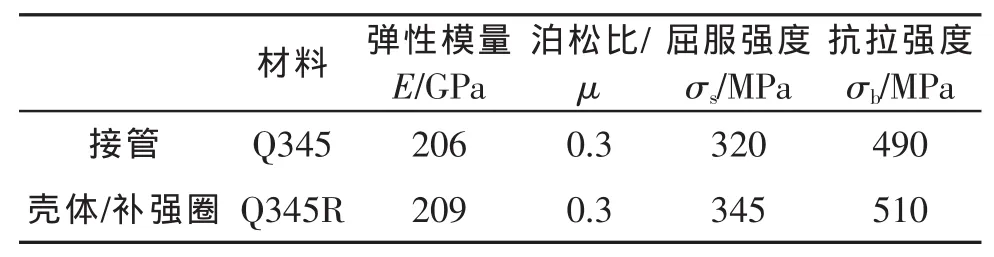
表1 Q345R和Q345机械性能参数

图1 Q345R和Q345的应力-应变曲线

金属材料的强化规律比较复杂，一般用简化的模型表示。目前广泛采用的强化模型有两种定义：等向强化 （屈服面大小变化）和随动强化 （屈服面在应力空间中平动）。本文选择等向强化。

等向强化的von Mises屈服评价准则公式如下：

式中，σe是von Mises等效应力，σy代表屈服强度。

等向强化准则的屈服面公式为：

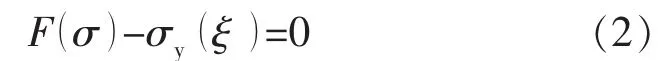
式中，F（σ）是关于压力的标量函数，σy（ξ）是屈服应力，与材料内部变量ε的函数有关。

在本文研究中，ANSYS中设置的双线性等向强化模型的数据从图1的应力-应变曲线中获得。

1.2 有限元分析模型

圆柱壳开孔接管结构如图2所示。筒体内径Di为 700 mm，壁厚δ为8 mm，长度lr为1000 mm；接管外径Do=377 mm，壁厚δt为8 mm，长度ln为250 mm。补强圈宽度为500 mm，壁厚为8 mm。由于图形关于xoy，yoz平面对称，所以选取原模型的1/4结构进行建模，选择solid 95单元进行分析计算。对模型进行分块处理，相贯区域进行网格加密，远离相贯区则划分稀疏的网格，以保证计算的精度和节约性。有限元模型及网格划分如图3所示。

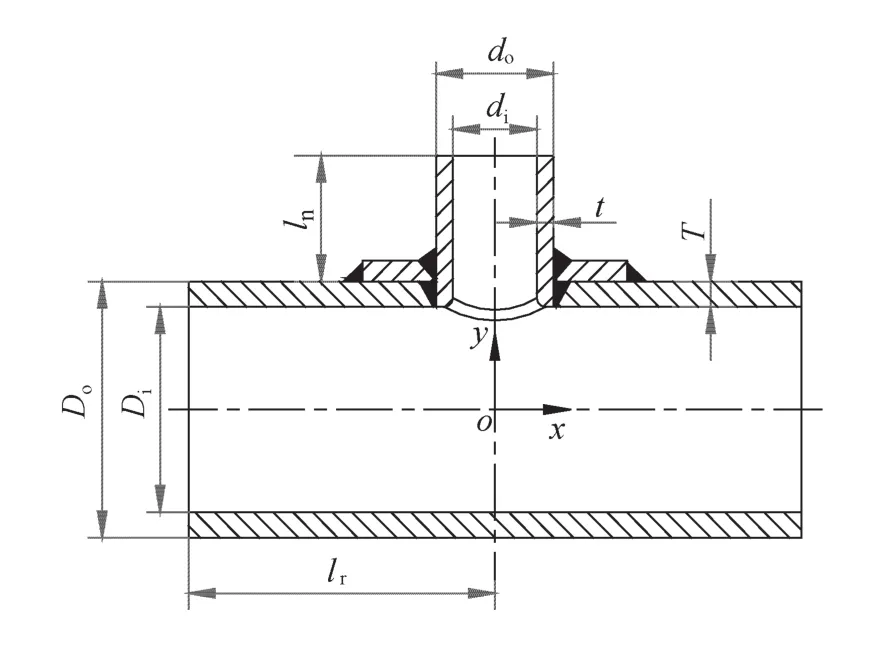
图2 圆柱壳开孔补强结构

图3 有限元模型及网格划分

在对称截面施加对称性约束，并在筒体的下边缘施加y方向的固定约束，限制筒体的刚性位移。筒体和接管的端面分别施加轴向应力σn和σt，筒体和接管内表面施加内压Pi，见图4。

2 计算结果与分析

2.1 应力分布云图

图5为应力分布云图。由图5可见，在圆柱壳与开孔接管的相贯区域存在应力集中区。本文采用线处理法，将危险界面的各应力分量沿着选定的路径进行线性化处理，然后按照JB 4732—1995进行应力分类及强度评定。

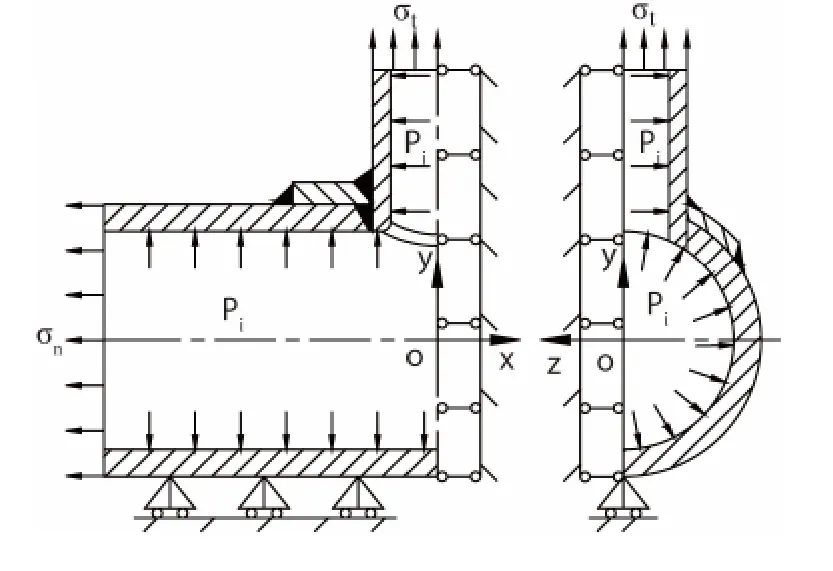
图4 载荷及边界约束

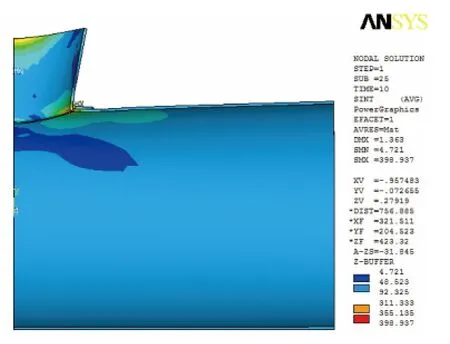
图5 应力分布云图

应力分类及评定的路线见图6。若不知道容器所能承受的极限压力，取的压力没有达到极限值，强度有很大的富裕量，这样所进行的强度评定就不合理。本文采取多次试取内压，直至到达容器所能达到的极限压力值时，再进行应力的分类及强度评定。

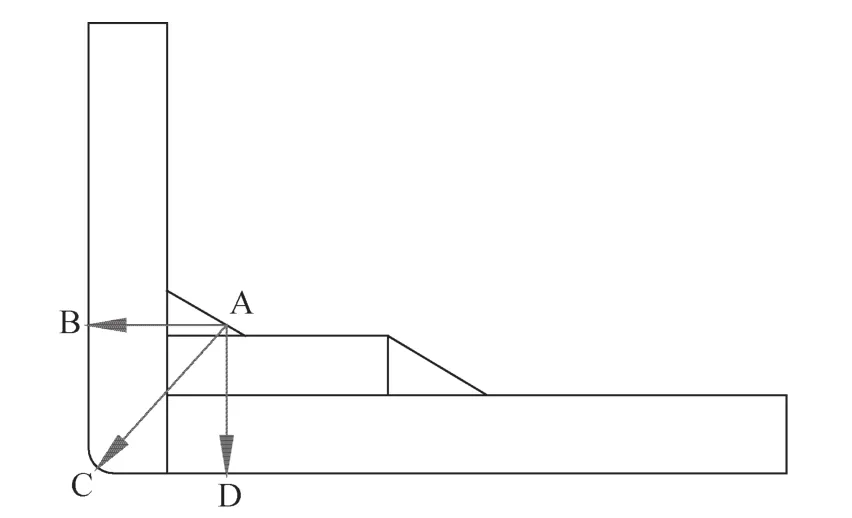
图6 应力评定路径

2.2 应力分类及强度评定

根据JB 4732—1995《钢制压力容器——分析设计标准》规定，由于设备的载荷工况不是非周期性载荷，所以不考虑峰值应力的影响。因此各种应力只需要满足下列条件：一次局部薄膜应力强度PL≤1.5Sm；一次局部薄膜应力加一次弯曲应力的组合应力强度PL+Pb≤1.5Sm；一次应力加二次应力的组合应力强度PL+Pb+Q≤3Sm；一次总体薄膜应力强度 Pm≤1.5Sm[5-6]。

筒体和补强圈的材料Q345R的设计应力强度Sm=170 MPa，接管材料Q345的设计应力强度Sm=163 MPa。K为载荷系数，其值和压力容器所受的载荷和组合方式有关，大小范围为1.0～1.25，本文取K=1.0。

采取逐步加载的方法确定容器极限承载压力。从0.8 MPa开始试取，在内压达到1.1 MPa时，已经超过容器所能承受的应力强度，但是压力取1.0 MPa，应力强度满足，且富裕量很小，故极限应力约为1.0 MPa。评定结果见表2。

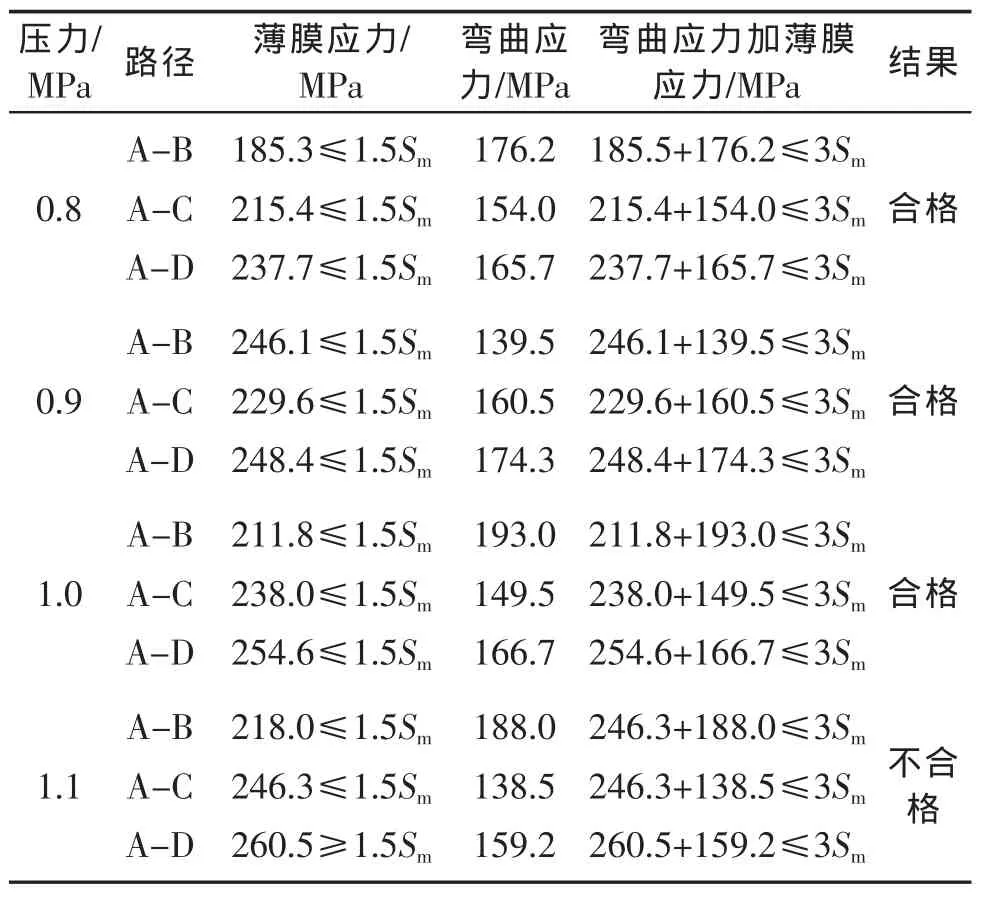
表2 评定结果

2.3 应力线性化分布规律

当施加的内压为1 MPa时，对容器的应力线性化分布规律进行分析。由图7可知，路径A-B上，外壁处的第一主应力最大，沿着路径逐渐降低；第二主应力和第三主应力从接管内壁处向接管外壁处逐渐降低，且应力在焊缝处有较大变化。图8为路径A-B的应力强度曲线。由图9可知，路径A-C上，外壁处的第一主应力较大，沿着路径先增大再减小；第三主应力从接管外壁处向接管内壁处逐渐减小。图10为路径A-C的应力强度曲线。由图11可知，沿着筒体上A-D路径，第一主应力的总体变化趋势是先上升后下降，再降低；第二和第三主应力总体呈上升趋势。图12为路径A-D的应力强度曲线。

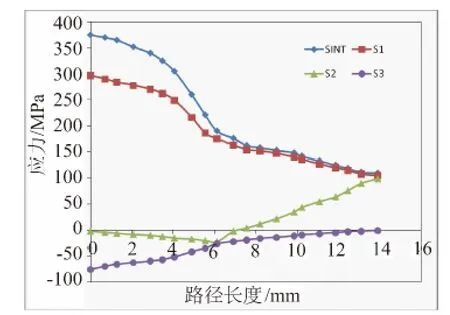
图7 路径A-B的应力图

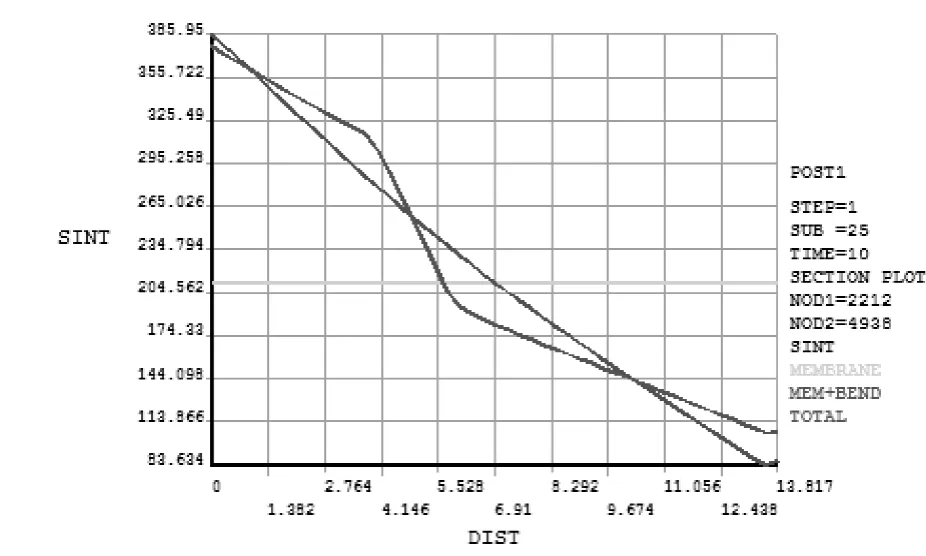
图8 路径A-B的应力强度曲线

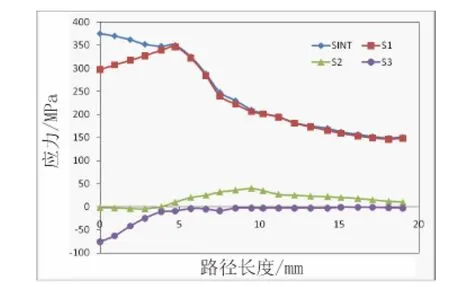
图9 路径A-C的应力图

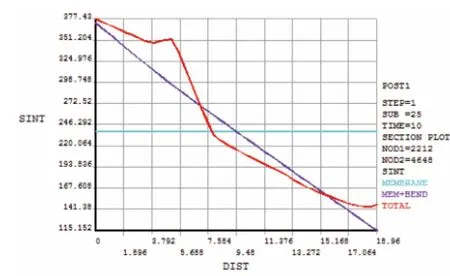
图10 路径A-C的应力强度曲线

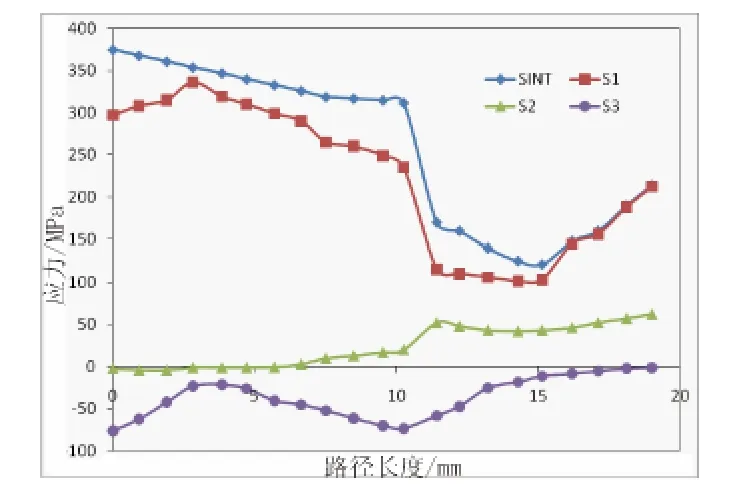
图11 路径A-D的应力图

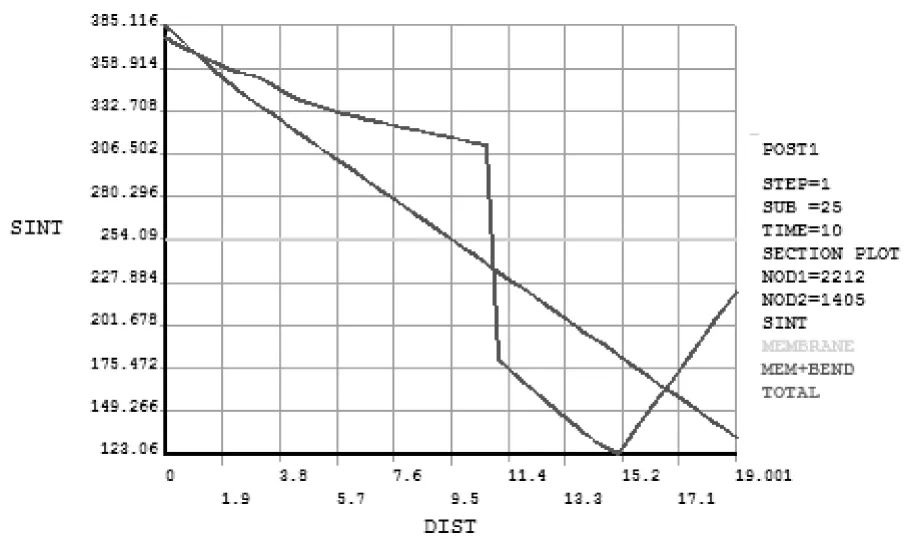
图12 路径A-D的应力强度曲线

2.4 应力集中系数

筒体和接管相贯区的外表面应力集中系数K沿着路径方向呈现出一定的变化规律，如图13所示，即先有一个平缓的过渡阶段，然后急剧下降，趋向于1。相贯区域的内表面同样存在着应力集中，且应力集中的变化规律为从路径起始点向终点逐渐衰减。

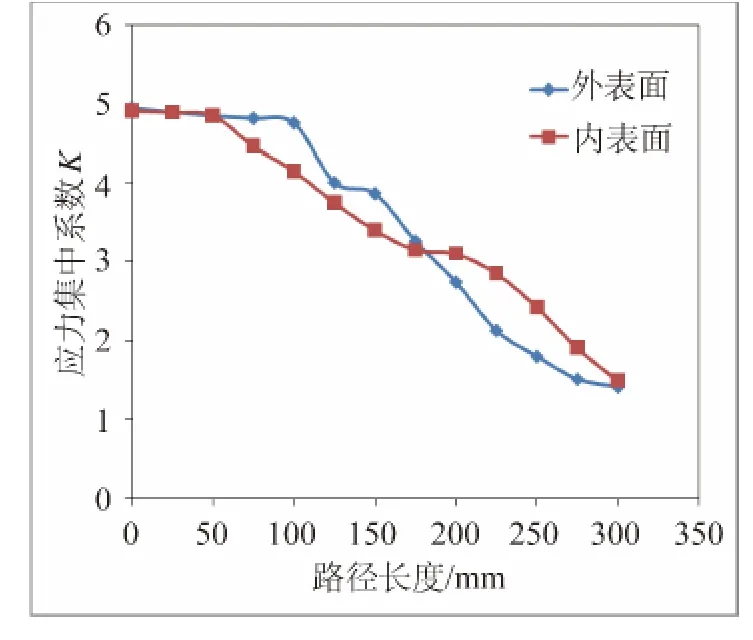
图13 相贯区表面应力集中系数分布

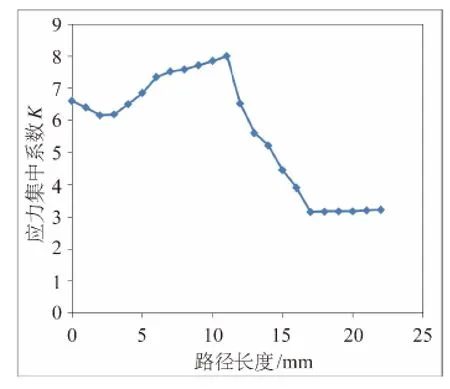
图14 相贯区壁厚方向应力集中系数分布

相贯区沿壁厚的应力集中系数分布如图14所示，这个区域的应力集中与路径的关系较为复杂，跨过了补强圈、筒体、接管，因位置的不同，对应的应力分布影响也有很大的差异。沿着路径，应力集中系数值先缓慢降低至一个波谷，然后上升至波峰，再下降直至趋于平缓，且最大值不超过9。

2.5 分析设计与常规设计的对比

ASME BPVC（锅炉及压力容器规范）第三卷对内压作用下的容器开孔接管的应力集中系数给出了计算公式：

根据本文有限元分析计算获得应力强度最大值与筒体未开孔时的应力强度值，相比较得出应力集中系数：

3 结论

采取模型的1/4部分进行研究，获得了圆柱壳体仅受内压作用时的应力分布情况，明确了其应力集中区域位置位于两者相贯区域。开展应力分类和强度评定，确定了容器的极限承载能力；获得了筒体与接管相贯区内外表面的应力集中系数变化规律，并将分析获得的最大应力集中系数与标准中经验公式计算结果进行对比，验证了数值模拟结果的正确性。该计算方法为圆柱壳开孔接管强度评定和结构优化提供了理论参考。

[1] 中华人民共和国国家质量监督检验检疫总局.锅炉和压力容器用钢板 [S].北京：中国标准出版社，2008.

[2] 中华人民共和国国家质量监督检验检疫总局.低合金高强度结构钢 [S].北京：中国标准出版社，2008.

[3] 中华人民共和国国家质量监督检验检疫总局.压力容器 [S].北京：中国标准出版社，2011.

[4] ASME，BPVC，SectionⅧ，Division 2[S].2010.

[5] 全国压力容器标准化技术委员会.钢制压力容器——分析设计标准 [S].北京：中国标准出版社，1995.

[6] 郑津洋，董其伍，桑芝富.过程设备设计 [M].北京：化学工业出版社，2010.