汽车防护杠用大口径薄壁钢管绕弯成形工艺参数优化*

刘志文，董菲菲，李落星，姚再起

(1.湖南大学，汽车车身先进设计制造国家重点实验室,长沙 410082; 2.湖南大学机械与运载工程学院，长沙 410082; 3.浙江吉利汽车研究院有限公司，杭州 311228)



2015148

汽车防护杠用大口径薄壁钢管绕弯成形工艺参数优化*

刘志文，董菲菲，李落星，姚再起

(1.湖南大学，汽车车身先进设计制造国家重点实验室,长沙 410082; 2.湖南大学机械与运载工程学院，长沙 410082; 3.浙江吉利汽车研究院有限公司，杭州 311228)

采用理论计算、数值仿真和实验相结合的方法探讨了材料、有无芯轴、芯头个数和芯棒伸出量对汽车防护杠用不锈钢管绕弯成形质量的影响。结果表明：相同工艺条件下，不锈钢SUS304管材比碳素钢Q235A更易产生截面畸变，但外侧壁厚减薄率较小；材料相同时，有芯轴支撑管材切向压应力和拉应力最大值的差值较小，材料流动更加均匀，能很好地抑制管材的截面畸变和失稳起皱；芯头个数是影响截面变形的最重要因素，芯头个数为3时，截面畸变率最小，其最大值仅为4.2%；芯棒伸出量过小，管材内侧容易起皱，截面畸变率较大；而伸出量过大时，管材外侧壁厚减薄严重，甚至导致拉裂；芯棒伸出量为9mm时，管材的弯曲成形质量最好。仿真结果与理论解析解和实测值吻合较好。

汽车防护杠；大口径薄壁管；绕弯成形；工艺参数；数值仿真

前言

大口径薄壁管材由于能够满足结构件的轻量化和强韧化要求，已广泛应用于汽车、航空航天、机械和石油管道等领域[1]。然而由于大口径管材空心、壁薄，绕弯成形过程中易产生壁厚减薄、截面畸变、失稳起皱和拉裂等缺陷会严重影响产品的成形质量。因此，对薄壁管材绕弯精确塑性成形关键理论与技术的研究，已成为现代塑性加工技术的迫切需求[2]。影响管材绕弯成形质量的因素较多且作用复杂，涉及材料、几何特征和边界非线性等多重因素相互耦合影响[3-4]，单纯采用理论解析方法难以高效准确地解决管材绕弯实际生产过程中出现的众多缺陷问题。数值仿真技术具有计算精度和效率高，信息量大等优点，而且还能兼顾各因素的耦合影响，为解决这一问题提供了新思路和新方法[5-7]。近几年国内外已有大量学者采用理论解析法、试验和数值仿真技术等方法对薄壁管材绕弯成形过程的应力应变变化、影响成形缺陷的工艺参数等进行了广泛研究，并推导了适用的芯轴参数选取公式，但主要工作集中在小口径薄壁管、型材方面，外径尺寸一般不大于50mm[8-12]。而对影响汽车防护杠用大口径薄壁钢管绕弯成形质量的工艺参数的研究则相对缺乏。

本文中以某汽车零部件制造企业生产的防护杠用大口径、大曲率薄壁钢管为研究对象，首先根据理论计算初步确定了芯轴参数，建立了薄壁管绕弯成形的精确有限元模型。采用数值仿真和实验相结合的方法，系统研究了不同材料、有无芯轴、芯头个数和芯棒伸出量对管材绕弯成形缺陷的影响规律，为确定最佳成形工艺参数，获得优质的弯曲管材提供理论指导，从而提高一次试模质量，缩短开发周期，降低制造成本。

1 芯轴参数理论模型

芯轴作为管材绕弯成形的重要工具，由芯棒、芯头和铰链组成，芯棒与芯头和芯头之间由铰链连接。芯轴主要在弯曲成形过程中对管材起支撑作用，避免管材截面严重畸变。

芯轴参数是影响大口径薄壁圆管绕弯成形质量的关键因素之一。芯轴参数主要包括芯头个数、芯棒伸出量、芯棒直径和芯头节间距等。合适的芯轴参数不仅可以降低壁厚减薄率，抑制管材外侧拉裂和内侧失稳起皱，而且能够降低管材的截面畸变[11]。由于实验使用的柔性芯头直径和芯头节间距已定，因此只须初步确定芯头个数和芯棒伸出量。图1为管材有芯绕弯成形工作原理图，管材绕弯曲模中心轴沿顺时针方向旋转，其中，t为管材壁厚，R为弯曲半径，D为管材外径，e为芯棒伸出量，表示芯棒端头与弯曲切点的距离，n为芯头个数，d为芯棒直径，r为芯轴圆角半径，k为芯头厚度，p为芯头节间距，α为芯棒和各个芯头转角的总和。

根据工模具之间的相对位置关系，由勾股定理可以推算出芯棒伸出量的值为

(1)

在芯模内侧有

(2)

在芯模中心有

(3)

根据生产实践经验，绕弯成形时芯头对应的圆心角一般不超过30°，否则可能导致截面变形过大，因此有如下关系[12]：

(4)

考虑到芯头的干涉问题，则有

(5)

芯头个数主要取决于芯棒和各个芯头转角的总和α的值，而α由管材的相对弯曲半径和壁厚等工艺参数确定。根据理论解析解，管材最大截面畸变发生的位置一般大于45°[13]，因此管材需要支撑的弯曲弧度对应α角的取值应该大于45°。实验中，管材和工模具各参数的取值分别为：D=76mm，d=73.3mm，t=1.2mm，R=150mm，r=1mm，p=42mm，k=31.5mm。代入式(1)计算得芯棒伸出量e≈8.7mm。由式(2)～式(5)得出芯头个数n>2.53。在实际生产中视情取整。芯轴参数解析计算模型为数值仿真工艺参数的快速选取提供理论指导。

2 管材绕弯成形仿真建模关键技术

2.1 材料的本构模型

采用LS-DYNA非线性有限元软件仿真绕弯成形过程。弯管材料本构方程选择MAT_24多线性弹塑性模型，其真实应力应变曲线由单向拉伸实验获得。实验采用汽车防护杠常用的两种材料：SUS304不锈钢和Q235A碳素钢，在管材中间平行部分参照国标GB/T228.1—2010制备拉伸试样，拉伸速度为3mm/min。两种材料的真实应力应变曲线和基本力学性能参数分别如图2和表1所示。弯曲模、芯棒和压块等其它工模具则采用MAT_20刚体材料模型。

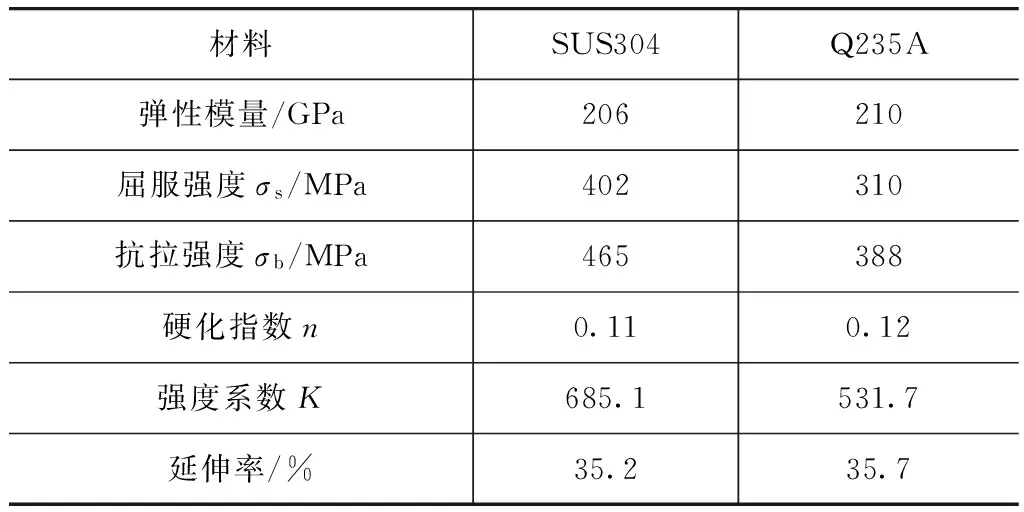
材料SUS304Q235A弹性模量/GPa206210屈服强度σs/MPa402310抗拉强度σb/MPa465388硬化指数n0.110.12强度系数K685.1531.7延伸率/%35.235.7

2.2 有限元网格模型

基于Hypermesh前处理软件建立薄壁钢管绕弯成形的有限元网格模型(图3)。管材、弯曲模、芯轴、压块和夹块等均采用四节点壳单元模拟。为精确地模拟薄壁钢管绕弯成形过程，其中管材采用LS-DYNA 16号单元公式，沿厚度的积分点为5个，而工模具网格采用2号单元公式，沿厚度的积分点为2个。在弯曲成形过程中，须进行沙漏控制，对于16号单元公式，采用8号公式沙漏算法，沙漏因子取值0.05。为减少计算时间，提高仿真精度，采用自适应网格技术对管材弯曲变形量大的区域进行网格局部细化。

2.3 工艺条件和接触边界模型

仿真和实验弯曲成形的主要工艺条件如表2所示。采用关键字“Part_inertia”使弯曲模、夹块和镶块以0.01rad/ms的角速度绕Z轴旋转。压块以1.18mm/ms的线速度沿X轴水平方向运动，约束YZ方向的平动自由度和所有转动自由度。防皱板在弯曲过程中保持静止不动。采用柱形铰链连接方式对芯棒、芯头和各芯头之间的运动状态进行约束；使用罚函数法计算接触界面力，刚度因子slsfac参数取值0.01；接触类型选择“FORMING-ONE-WAY”单面接触方式。管材与工模具之间的摩擦对弯曲成形质量有重要影响。本文中选取经典库仑摩擦模型来定义管材和工模具之间的接触状况。根据文献[14]中获得的摩擦稳定条件，定义各界面之间的摩擦因子，如表3所示。

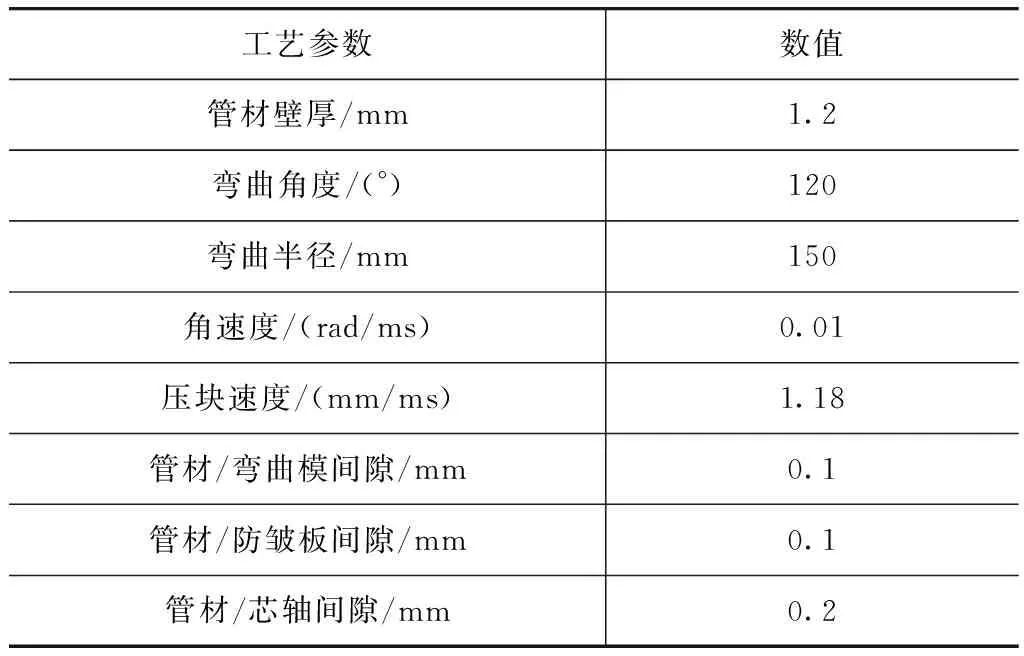
表2 弯曲成形主要工艺条件

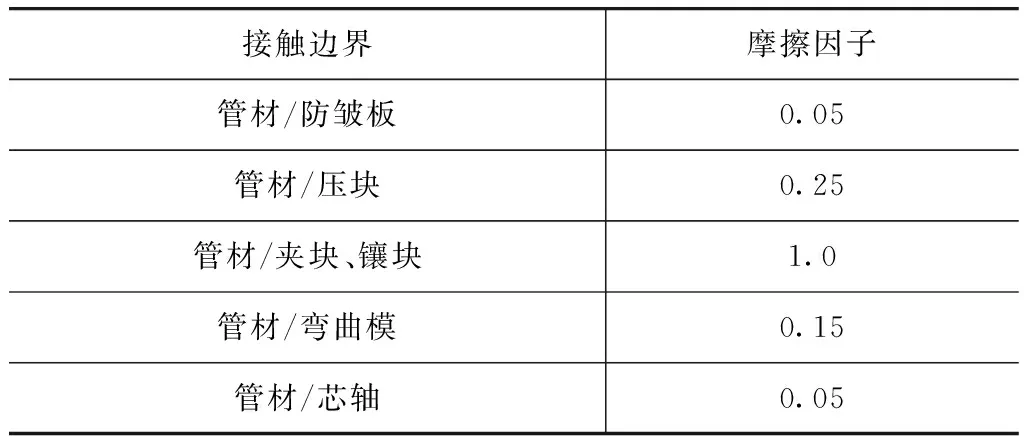
表3 各接触边界摩擦因子定义

3 弯曲成形质量评判标准与模型验证

3.1 管材壁厚减薄和截面畸变的评判标准

壁厚减薄率将直接影响着管材的刚度和强度等机械性能，严重制约了管材的使用。弯曲前后的壁厚变化率用δt来表示，即

(6)

式中：t0和t分别为管材弯曲前后的壁厚值。

根据文中薄壁管弯曲角为120°的特定情况，壁厚测量位置的选取方法为：将管材弯曲变形区平均分成4份(图4)，从压块端沿绕弯方向每隔30°取一个平面，然后测量和计算该截面最外侧部位的壁厚减薄率。

弯曲前后的截面畸变一般采用椭圆率φ来表示，即

(7)

式中：D0为管材初始直径；Dmax和Dmin分别为绕弯成形后管材同一截面上水平和垂直方向测得的最大和最小外径，如图5所示。

3.2 仿真模型准确性验证

绕弯成形实验在型号为CNC80TMRE的绕弯机上进行。薄壁管材采用Q235A碳素钢，外径为76mm，壁厚为1.2mm，弯曲角度为120°，弯曲半径为150mm，芯头个数3个，其余工艺参数见表2。管材与夹块、镶块间采用砂纸来增大摩擦，以保持无相对滑动，管材与压块之间为干摩擦，其余工模具边界均采用润滑脂润滑。

图6(a)为芯棒伸出量为9mm时，管材弯曲变形区5个截面上最内外侧壁厚仿真与实测值的对比。由图可见，仿真与实测结果基本一致，相对误差不超过10%。图6(b)为芯棒没有伸出，其他条件保持不变时的起皱位置和个数的实验与仿真结果。由图可知，两者的起皱个数均为12个，位置也基本相符。验证了所建有限元模型的准确性。

4 结果分析与讨论

4.1 材料参数对弯曲成形质量的影响

绕弯成形是一个涉及材料非线性的复杂过程，不同的材料自身的抗弯曲能力不同，而且材料参数还影响弯曲管材的应力应变响应。本文中选用SUS304不锈钢作为Q235A碳素钢的对比材料，取芯棒伸出量e=9mm，芯头个数n=3，其他工艺条件相同。图7为两种不同材料下管材的壁厚减薄率和截面畸变率。由图7(a)和图7(b)对比可见，在相同的工艺条件下，SUS304材料的壁厚减薄率比Q235A小，但截面畸变率则较大。由表1可知，SUS304管材的应变硬化指数n比Q235A略小，而屈服强度σs和强度系数K比Q235A要大。在相同的工艺条件下，Q235A管材的屈服强度较小，先发生屈服进入塑形变形阶段，然而由于其硬化指数n比其它钢材小得多，在相同弯曲角度下，应力中性层内移量增大，导致外侧壁厚减薄率较大；文献[15]中指出材料的强度系数K越大，弯曲成形过程产生塑形变形能越大，使管材截面形状变化也越大。与Q235A管材相比，SUS304管材的强度系数K值相对较大，因而更容易产生截面畸变。

图8为弯曲成形过程中两种管材的切向应力随时间的变化曲线。由图可知，Q235A管材内外侧的切向应力值比SUS304小，且随时间的变化较小，因而其绕弯成形过程中材料塑性变形和压应力的整体分布也相对更加均匀，因此不容易发生截面变形和失稳起皱。

表4为相同工艺条件下两种材料的管材弯曲成形质量仿真和实验结果，SUS304管材变形区内侧平面出现不平整和局部内凹，而Q235A材料内侧表面光滑，验证了与Q235A管材相比，SUS304管材弯曲成形过程中材料变形不均匀，截面容易畸变。

表4 相同工艺条件下不同材

4.2 有无芯轴支撑对弯曲成形质量的影响

图9为有无芯轴支撑时Q235A管材的弯曲成形质量仿真结果。由图可知，无芯轴支撑时，管材弯曲变形不充分，外侧材料已严重塌陷，截面畸变严重；而使用芯头和芯轴支撑时，有效抑制了管材外侧塌陷，横截面圆度保持很好，无明显起皱现象。

图10为有无芯轴支撑时Q235A管材切向应力极大值随弯曲进程的变化。对比可知，有芯轴支撑时，管材内外侧的压缩和拉伸变形区受到芯棒的刚性约束，切向压应力和拉应力极大值的差值小于无芯棒支撑时的差值，从而很好地遏制了应力中性层向内侧偏移，减少了管材截面畸变和失稳起皱等的发生趋势。同时，有芯轴支撑时，管材弯曲变形区参与变形的金属增多，变形区域相应增大，切向拉应力和压应力极大值随弯曲进程的变化较平缓，材料流动和应力分布也较均匀。因此，使用芯轴支撑时显著减少了管材截面畸变和内侧失稳起皱等现象。

4.3 芯头个数对弯曲成形质量的影响

图11为相同工艺条件下，芯头个数对Q235A管材壁厚减薄率和截面畸变率的影响。由图11(a)可知，芯头个数增加，外侧壁厚减薄率呈增大趋势。芯头个数为1时，最大减薄率为19.4%；当芯头个数增加到2时，最大减薄率急剧增大，达到22.4%；再增大芯头个数，最大减薄率增加缓慢。随着芯头个数的增加，管材外侧受到的切向拉应力逐渐增大，相应的金属纤维伸长量增大，导致壁厚减薄率增加。由图11(b)可知，随着芯头个数的增加，截面畸变率逐渐减小。芯头个数对管材的截面畸变影响非常显著，当芯头个数为1时，最大截面畸变率约为22%，弯曲塑性变形区得不到足够的支撑，导致应力分布不均匀，截面变形严重。当芯头个数逐渐增加到3时，最大截面畸变率控制在4.2%。再增加芯头个数到4时，最大截面畸变率减少不明显，两者仅相差1.2%。即当芯头个数超过理论解析解以后，对截面变形的抑制作用便大大减弱。

表5为不同芯头个数的管材弯曲成形质量。由图可知，芯头个数为1时，管材的外截面出现明显塌陷。当芯头个数增加到3时，管材的外侧截面圆度保持很好。在绕弯过程中，管材的有效弯曲变形区得到芯头的刚性支撑，能很好地抑制截面畸变。然而，再继续增加芯头个数，芯头进入弯曲段的长度也相应增加，成形后难以抽芯，容易划伤管材内壁，严重时导致芯头拉断。综合考虑，芯头个数为3时管材弯曲成形质量最好。

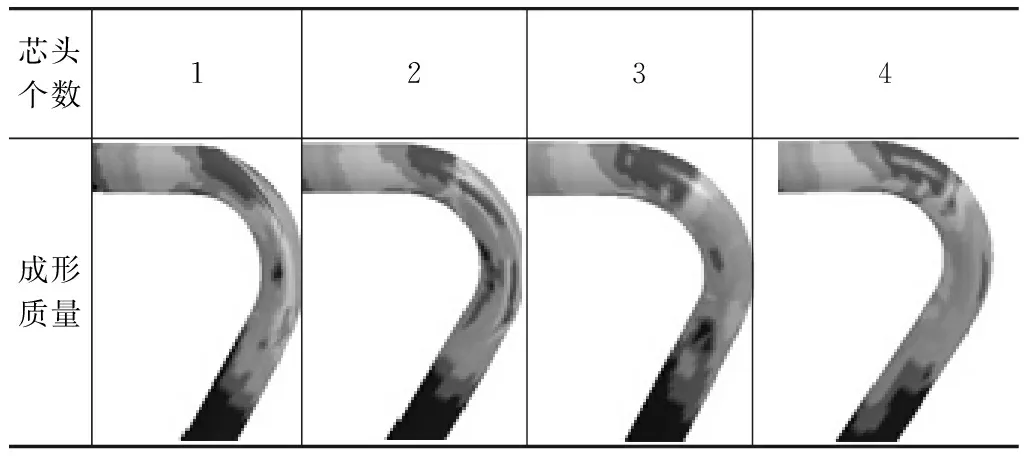
表5 不同芯头个数的管材弯曲成形质量

4.4 芯棒伸出量的影响

图12为不同芯棒伸出量下Q235A管材的壁厚减薄率和截面畸变率。由图12(a)可知，芯棒伸出量对壁厚减薄率的影响比芯头个数显著。随着芯棒伸出量的增加，外侧壁厚减薄率逐渐增大。这是因为增加芯棒伸出量，增大了芯棒与管材内壁的接触面积，导致芯棒与管坯之间的摩擦增大，阻碍了管材的顺利流动，管材外侧受到的拉应力相应增大，因此外侧壁厚减薄加剧。由图12(b)可以看出，随着芯棒伸出量的增加，管材截面畸变率下降。因为增加芯棒的伸出量，增大了芯模的支撑作用，对保持管材的截面圆度作用明显。在绕弯前30°范围内，由于3个芯头对管材的有效支撑，截面畸变率很小，超过30°时，支撑作用减弱，截面畸变率增大。

图13为不同芯棒伸出量的管材弯曲成形试验结果。由图可以看出，当芯棒伸出量为0时，管材内侧产生了明显的起皱。随着芯棒伸出量的增大，芯棒与管坯之间摩擦增大，使弯曲变形区内侧受到的切向压应力减小，同时管坯塑性变形区受到芯棒的刚性约束区域也有所增大，使失稳起皱逐渐减小；然而当芯棒伸出量过大时，在弯曲后端外侧切点部位产生材料聚集，导致管材局部凸起，如图13(c)所示；芯棒前端的材料由于受到过大的拉力而发生拉伸，出现开裂，见图13(d)。因此，增大芯棒伸出量，虽然管材截面畸变和内侧起皱趋势得到一定改善，但是容易造成管材外侧壁厚减薄严重，导致拉裂。在实际生产中，要全面考虑其对各缺陷的影响，合理确定芯棒伸出量的大小。因此，由仿真和实验结果确定芯棒伸出量选取为9mm。

5 结论

(1) 在相同的工艺条件下，SUS304管材比Q235A更易产生截面畸变，但外侧壁厚减薄率小。

(2) 有芯轴支撑时管材切向压应力和拉应力极大值的差值小于无芯棒支撑时的差值，材料流动更加均匀，很好地抑制了管材截面畸变和内侧失稳起皱。

(3) 随着芯头个数的增加，管材截面畸变率逐渐减小，外侧壁厚减薄率呈增大趋势。芯头个数是影响截面变形的最重要因素。芯头个数为3时，最大截面畸变率控制在4.2%。

(4) 随着芯棒伸出量的增加，管材的外侧壁厚减薄率逐渐增大，截面畸变率下降。芯棒伸出量过小，管材内侧会产生起皱；而伸出量过大时，外侧壁厚减薄严重，前端甚至产生拉裂。芯棒伸出量为9mm时，管材的弯曲成形质量最好。

[1] 刘劲松,张兴华,刘海,等.薄壁钢管内胀推弯成形数值模拟及实验研究[J].锻压技术,2012,37(2):63-67.

[2] Li Heng, Yang He, Zhan Mei. The Interactive Effects of Wrinkling and Other Defects in Thin-walled Tube NC Bending Process[J]. Journal of Materials Processing Technology,2007,187/188:502-507.

[3] Tang Ding, Li Dayong, Yin Zhongwei, et al. Roles of Surface Booster System on Bending of Thin-Walled Copper Tube[J]. Journal of Materials Engineering and Performance,2009,18(4):369-377.

[4] Qureshi H A, Russo A. Spring-back and Residual Stresses in Bending of Thin-walled Aluminium Tubes[J]. Materials and Design,2002,23(2):217-222.

[5] Yang He, Li Heng, Zhang Zhiyong, et al. Advances and Trends on Tube Bending Forming Technologies[J]. Chinese Journal of Aeronautics,2012,25:1-12.

[6] Wang Jyhwen, Rohit Agarwal. Tube Bending Under Axial Force and Internal Pressure[J]. Journal of Manufacturing Science and Engineering,2006,128:598-605.

[7] Hasanpoura K, Amini B, Poursina M, et al. The Effect of Anisotropy on Thin-Walled Tube Bending[J]. AIP Conference Proceedings,2011,13(83):187-193.

[8] Tang N C. Plastic-deformation Analysis in Tube Bending[J]. International Journal of Pressure Vessels and Piping,2000,77:751-759.

[9] 温彤,丰慧珍,艾百胜.管材绕弯变形的理论与实验分析[J].重庆大学学报(自然科学版),2006,29(12):8-12.

[10] Peek R. Wrinkling of Tubes in Bending from Finite Strain Three-dimensional Continuum Theory[J]. International Journal Solids Structure,2002,39:709-723.

[11] 沈化文,刘郁丽,董文倩,等.芯棒对铝合金矩形管绕弯回弹作用的数值模拟[J].材料科学与工艺,2012,20(1):38-43.

[12] Li Heng, Yang He, Zhan Mei, et al. Role of Mandrel in NC Precision Bending Process of Thin-walled Tube[J]. International Journal of Machine Tools & Manufacture,2007,47:1164-1175.

[13] 刘婧瑶,唐承统,宁汝新,等.薄壁管数控弯曲成形中芯轴参数的确定[J].机械设计与研究,2008,24(5):70-73.

[14] Yang He, Li Heng, Zhan Mei. Friction Role in Bending Behaviors of Thin-walled Tube in Rotary-draw-bending Under Small Bending Radii[J]. Journal of Materials Processing Technology,2010,210:2273-2284.

[15] 董文倩,刘郁丽,杨合.材料参数对3A21矩形管弯曲回弹的敏感性分析[J].材料科学与工艺,2011,19(5):1-5.

Process Parameters Optimization of Rotary Draw Bending for LargeDiameter Thin-walled Steel Tube for Automotive Bumper

Liu Zhiwen1,2, Dong Feifei1, Li Luoxing1,2& Yao Zaiqi3

1.HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082; 2.CollegeofMechanicalandVehicleEngineering,HunanUniversity,Changsha410082; 3.ZhejiangGeelyAutomobileResearchInstituteCo.,Ltd.,Hangzhou311228

A method of combining theoretical calculation, numerical simulation and experiments is used to investigate the effects of material, with or without mandrel, number of mandrel ball and the protrusion of mandrel shank on the rotary draw bending quality of a stainless steel thin-walled tube for automotive bumper. The results show that under a same process condition, the SUS304 stainless steel tube is more prone to cross-section distortion, but with a less thinning rate in outer wall, compared with Q235A carbon steel tube. With a same material, when mandrel support is adopted the difference between the peak tangential tensile stress and peak tangential compressive stress becomes smaller with a more uniform material flow, which can better avoid section distortion and wrinkling. The number of mandrel ball plays a dominant role in restraining cross-section distortion. When three mandrel balls are used, a minimum section distortion rate (4.2% at most) can be achieved. The protrusion of mandrel shank should also properly be selected: too small a protrusion is prone to wrinkling in inner wall or section distortion while too large a protrusion may lead to severe thinning or even cracking in outer wall, and it is found that the best quality of rotary draw bending for thin-walled tube can be achieved with a 9mm protrusion of mandrel shank. The results of simulation and analytical solutions well agree with measured ones.

automotive bumper; large diameter thin-walled tube; rotary draw bending; process parameters; numerical simulation

*国家“十二五”科技支撑计划项目(2011BAG03B02)、国家自然科学基金面上项目(751229039)、湖南大学汽车车身先进设计与制造国家重点实验室自主课题项目(61075005)和长沙市科技重大专项(K1204008-11-1)资助。

原稿收到日期为2013年11月12日，修改稿收到日期为2014年1月22日。