三元锂离子动力电池针刺热失控实验与建模*

张明轩，冯旭宁，欧阳明高，卢兰光，王 芳，樊 彬

(1.清华大学，汽车安全与节能国家重点实验室，北京 100084； 2.中国汽车技术研究中心新能源实验室，天津 300300)



2015130

三元锂离子动力电池针刺热失控实验与建模*

张明轩，冯旭宁，欧阳明高，卢兰光，王 芳，樊 彬

(1.清华大学，汽车安全与节能国家重点实验室，北京 100084； 2.中国汽车技术研究中心新能源实验室，天津 300300)

针对纯电动汽车锂离子动力电池存在的一个潜在安全问题，即热失控现象，本文中对某三元锂离子动力电池最为剧烈的一种热失控，即针刺热失控的过程进行研究。通过混合脉冲能力特性实验、热箱加热热失控实验和基于已有模型，搭建了描述针刺热失控过程的集总参数模型，并进行了实验。针刺模型的预测结果得到了针刺实验的证实，这为后续的研究和系统开发奠定了基础。

三元锂离子动力电池；针刺热失控；实验；建模

前言

纯电动汽车可实现零排放，且所使用的电能来自电网，被视为解决环境污染问题和能源危机的一种可行方案[1]。纯电动汽车作为一种交通工具，其速度、效率、续驶里程、使用寿命、安全性和成本必须达到实用标准。因此，纯电动汽车上的动力电池应满足以下几点要求：高能量密度；高功率密度；较长的循环寿命；使用维护方便；安全性能好；价格便宜[2]。综合考虑各方面的因素，相比于其他类型的蓄电池，锂离子电池具有显著的优势[3]。因此目前多数电动汽车都选用锂离子电池作为能量源。

然而，锂离子电池潜在的事故危险会打击消费者接受电动汽车的信心，并且危害人民群众的生命财产安全。锂离子电池的安全问题主要表现为热失控引起的起火和爆炸[4]。在小型商用锂离子电池单体(<3A·h)和电池组(<150W·h)领域，热失控问题已通过安全冗余设计满足了要求[5-6]，而对于汽车的大型锂离子单体(>6A·h)和电堆(>200W·h)而言，其热失控问题仍是一项挑战，主要原因有：(1)电动汽车的高功率要求限制了PTC(正温度系数元件)和其他安全器件的使用；(2)大型电池本身就更容易产生热失控，因为增加的电池容量降低了表面积体积比，这使单位体积的散热面积降低；(3)增加的电池容量加剧了电池内的温度分布差异，而在给定的表面热传递条件下，不均匀的电池温度分布导致局部温度较高而增加了产生热失控的可能性[7]。

建模是一种有效的研究大型锂离子单体热失控问题的手段。国内外目前已经有了多种类型的电池模型，包括以维度划分的集中质量模型、一维模型、二维模型、三维模型，以模型理论基础划分的电化学-传热耦合模型、化学-传热耦合模型[8]。但大多数模型的仿真都集中在单体加热实验上，少有对其他类型的滥用实验的仿真，尤其是最为严苛的且具有代表性的针刺实验，并且多数模型的研究对象都是18650这种小型圆柱电池。

本文中对特定型号的25A·h三元锂离子动力电池的热失控过程进行了研究，通过混合脉冲能力特性(HPPC)实验、热箱加热热失控实验，基于文献综述和已有模型，搭建了可以描述针刺过程的集总参数模型，并进行了实验验证。

1 三元锂离子电池热失控副反应

文献[9]～文献[11]中对锂离子电池热失控的机理做过综述性研究。三元锂离子电池有5个主要的热失控副反应：SEI膜分解反应、负极与电解液的反应、正极活性物质分解反应、粘结剂反应和电解液分解反应。这5个反应按照温度升高的顺序依次发生。

1.1 SEI膜分解反应

SEI膜分解反应在80～120℃之间开始发生，反应的动力学方程和放热方程[9]为

(1)

QSEI=HSEI·Wc·kSEI

(2)

式中：T为温度；cSEI为在卷层的碳成分中SEI膜亚稳态含量的无量纲数；kSEI为反应参数；R为气体常数，R=8.314J·mol-1·K-1；QSEI为单位体积的放热功率；其余参数列于表1中。

1.2 负极与电解液的反应

大约在120℃开始发生负极与电解液的反应，反应的动力方程[12]为式(3)，反应的放热方程形式与式(2)相同。

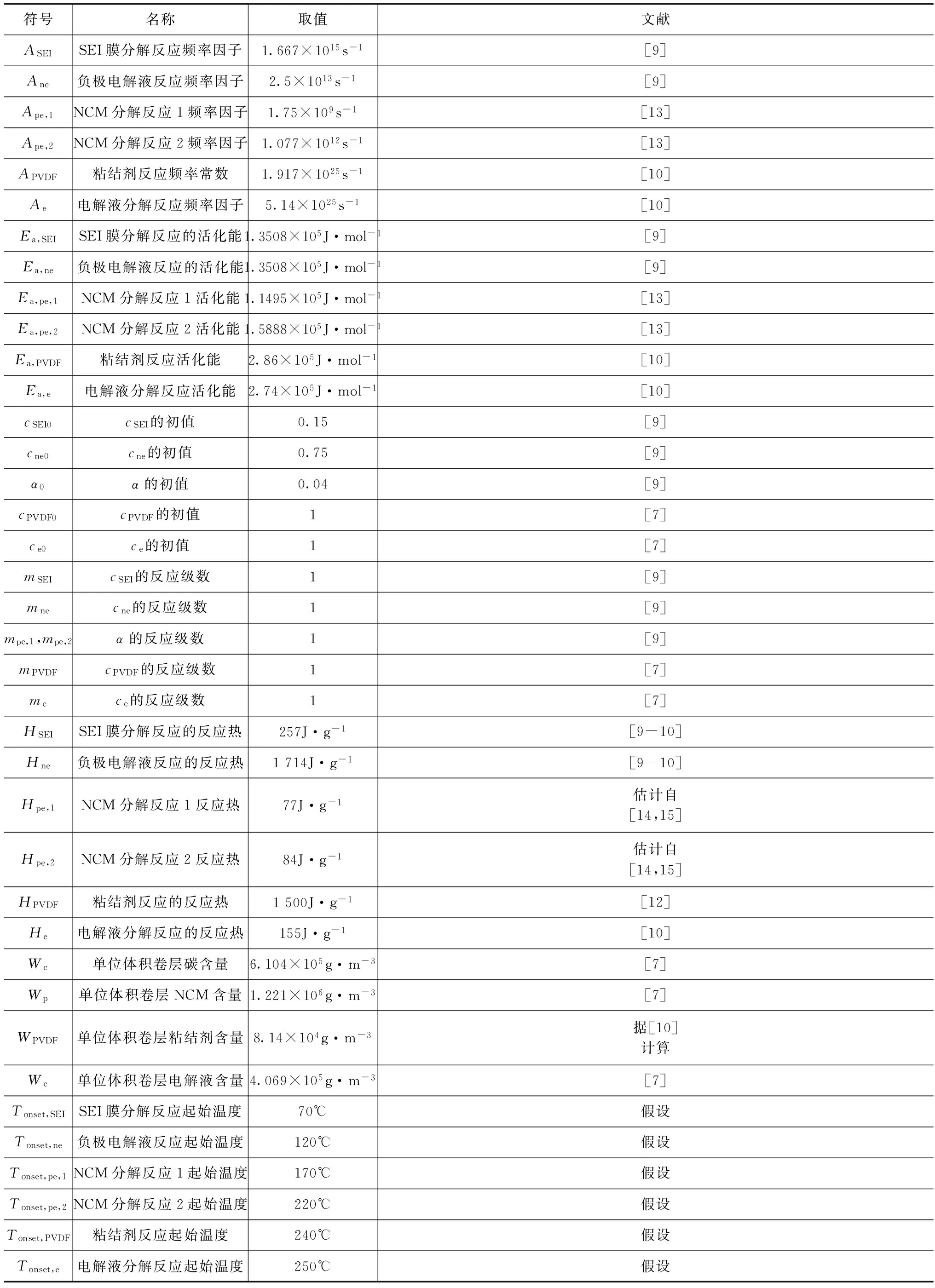
表1 热失控副反应特征参数

(3)

式中：cne为嵌入碳中的锂量的无量纲数；tSEI和tSEI,ref分别为SEI膜厚度和SEI膜的起始参考厚度的无量纲数；kne为反应参数；其余参数列于表1中。

需要注意的是，因为SEI膜隔开了电解液溶剂和负极材料，所以只有当SEI膜分解反应进行到一定程度，SEI膜剩余量较少(本文中假设cSEI<0.1)后，才会发生负极与电解液的反应。

此外，负极材料与电解液的反应会生成SEI膜的构成物质Li2CO3，即重新生成SEI膜。不过由于重新生成的SEI膜很不规则，所以不会阻碍负极材料与电解液的反应。但tSEI中需要计入新生成的SEI膜。

1.3 正极活性物质分解反应

当温度上升到200℃或以上时，开始发生正极活性物质分解反应，反应的动力方程[9]为式(4)，反应的放热方程形式与式(2)相同。

(4)

式中：cpe为电解液浓度的无量纲数；α为转化率；kpe为反应参数；其余参数列于表1中。NCM正极材料发生分解反应时会产生双放热峰[14-15]。所以三元锂离子电池正极活性物质分解反应的特征参数会有两组，对应不同的放热峰。

1.4 粘结剂反应

粘结剂的反应大约在240℃时开始发生，反应的动力方程[12]为式(5)，反应的放热方程形式与式(2)相同。

(5)

式中：cPVDF为粘结剂含量的无量纲数；kPVDF为反应参数；其余参数列于表1中。

1.5 电解质溶液分解反应

电解质溶液分解反应推进了整个热失控过程。电解质溶液分解反应发生时正极活性物质分解反应、粘结剂反应正在进行，三者一起放出大量的热，使电池温度急剧升高。反应的动力方程[7]为式(6)，反应的放热方程形式与式(2)相同。

(6)

式中：ce为电解液浓度的无量纲数；ke为反应参数；其余参数列于表1中。

2 主要仿真参数的获取

本文中建模对象选择了满足要求的精进能源公司生产的25A·h的大容量方壳三元锂离子电池。

为了进行建模仿真，须要知道电池的尺寸、质量和电学与热学等物理参数。其电学和热学参数主要通过HPPC实验和热箱加热热失控实验来获得。

2.1 HPPC实验结果

通过HPPC实验，获得了单体开路电压随SOC的变化规律(图1)和单体内阻随SOC的变化规律(图2)。

因为HPPC中使用的充放电电流将近1C，电池的极化现象影响显著，所以内阻在充放电初期会随时间有一个变化。这里选取较为接近电池稳定工作状态下内阻的30s放电内阻作为参考。

2.2 热箱加热热失控实验

单体的热箱加热热失控实验主要利用加速量热仪(ARC)完成。ARC可以跟踪内部研究对象的温度变化，模拟绝热环境。

为了测得单体的热容量，利用定功率仪器给电池单体加热，用ARC量热仪创造绝热条件，测量出电池单体在绝热和恒功率热源条件下的温度变化规律(图3)，对其进行拟合，进而得到单体热容的变化规律为

cp=2.134Tc+1020

(7)

在过热箱加热热失控实验过程中对单体的开路电压和内部温度进行跟踪测量，就可得到单体的开路电压随温度的变化规律。在实验过程中对单体周期性地进行短时间的0.1C的充放电(图4)，就可以得到单体内阻随温度的变化规律。

图5是单体的开路电压随温度的变化规律。用Matlab的Curve Fitting Tool以130℃为界对该曲线分段进行三阶拟合，可得拟合公式为

(8)

式中：U为开路电压；Tc为温度。

图6是单体内阻随温度的变化规律。利用Matlab的Curve Fitting Tool进行三阶拟合，得到内阻对温度的拟合公式为

r=(1.579×10-8)Tc3+(4.266×10-8)Tc2-

(2.155×10-4)Tc+0.02911

(9)

式中r为内阻。

该实验中得到的内阻明显高于2.1节中图2的结果。这是因为在本实验中为了防止大电流对单体的热失控副反应过程造成影响，仅使用了0.1C的充放电电流，而2.1节中的HPPC实验使用的充放电电流为1C。对于锂电池来说，电流越大则内阻越小，所以会有此差异。本实验中的起始温度在30℃以下，电池单体状况几乎与2.1节中100%的SOC时的状况完全一致，但内阻是它的2.87倍。

3 针刺热失控模型

3.1 模型的几何结构划分

多数电池模型只耦合两方面的因素，而针刺模型需要耦合热失控副反应、焦耳热和传热3方面的因素。如果继续使用传统的三维模型建模，会使模型结构复杂，计算量庞大。文献[16]中利用集总参数法进行简化的模块化模型可显著降低计算规模，且预测结果与实验数据吻合很好。本研究中也采用集总参数法简化模型。

因为研究对象25A·h三元锂离子电池属于大容量动力电池，体积、质量较大，加之针刺过程时间跨度较短，所以直接使用集总参数法进行仿真容易带来较大误差。因此研究中根据刺针所在位置先对电池进行分区(图7为示意图，其中中心圆点代表刺针，白线表示分区划分)，然后再按照分区利用集总参数法进行简化，得到最终的模块化模型(图8，弹簧代表等效热阻)。这样得到的模块化模型已经自然地包括了电池单体的传热学特征和刺针的位置等条件。

3.2 针刺模型理论基础

针刺模型的搭建以热失控副反应、焦耳热和传热3方面的理论为依据。

热失控副反应的理论基础已在前文叙述，故在此不再复述。

焦耳热方面的理论基础主要是电学相关理论，但为了应用这些理论，必须对电池和针刺过程做相应的简化假设。

研究中使用的25A·h三元锂离子电池单体内有两个电池软包，两个软包之间采用并联的方式连接。每个软包内的电池是由正极铝箔、负极铜箔及其之间的活性物质、电解液和隔膜卷绕而成的(图9)。

当有刺针刺入电池时，电池卷绕层被穿透，情况如图9所示。其中深色粗直线代表刺针。此时假想将电池层展开，就可以得到图10所示的等效情况[17]。在图10中，刺针被截断成了多个小段，它们之间相互并联。在模型中认为每一段刺针的地位是相同的，所以图10中并接它们的细实线之间不会有电流流过。由于两个电池软包是并联的，刺穿两个软包的刺针是同一条刺针，所以在电学上可将它们同时等效在图10中。

本研究中将电流在正极和负极之间的流动简化为均匀的流动，即在铜箔和铝箔之间的电流密度一致，所有刺针分段内的电流密度一致。

电池单体电压随温度的变化情况如式(8)所示，记为U1。在220～234℃这段区间内电池单体的电压取其平均值3.802 5V，在234℃时电池单体电压突降为0。电压随SOC的变化情况如图1所示，记为U2。利用插值法可以得到每种SOC状态下的电压。由于电压与温度的关系和电压与SOC的关系是不解耦的，所以不能简单地取两者变化比率的乘积作为最终电压的变化比率。简化起见，模型中取电池的电动势为min{U1,U2}。

电池单体内阻随温度的变化情况如式(9)所示，随SOC的变化情况如图2所示。如2.2节所述，大电流下的电池内阻小于小电流下的电池内阻。而在针刺过程相当于直接用电阻极小的钢针将作为正负极的铝箔和铜箔接通，会产生极大的短路电流，远大于1C。因此针刺过程中的电池内阻应远小于2.1节和2.2节中的结果。由图2可知，SOC大于40%时，内阻随SOC的变化较为平缓，而针刺过程中一般在SOC下降到30%以前就会发生热失控；由图6可知，在发生热失控之前的温度下，电池内阻随着温度的上升会有大幅度的改变。因此，针刺过程中电池内阻的变化主要受温度的影响，SOC的影响是次要的。综合上述两方面原因，选取式(9)作为内阻计算的基本公式，再乘以大电流下的修正系数得到最终的内阻。考虑到内阻不会随电流的增大无限制减小，故选取介于2.87-1～2.87-4之间的常数作为修正系数(模型中取为0.05)，其中2.87是0.1C与1C电流下测得的内阻的比值。

认为在单体内隔膜解体时，正极和负极的活性物质直接接触，发生剧烈反应，导致电压突降，并产生热失控。而正负极活性物质之间的反应释放的能量就是针刺短路过程中剩余的电化学能。利用2.1节中HPPC的实验结果可以求得该型25A·h三元锂离子动力电池的电化学能总量约为343 350J。刺针刺入时，单体在刺针位置上的隔膜被穿破，引起周围的正负极活性物质直接接触发生反应，并通过刺针导致短路；在234℃电压突降时认为隔膜解体，电池中剩余的电化学能瞬间释放。隔膜刺穿引起的正负极活性物质反应被认为发生在电池圆环分区中最靠近刺针的分区里，其放热功率须进行假设。假设在刺针刺入时，最靠近刺针的分区和被刺穿的部分的隔膜同时失效，因此，其放热功率等于在最靠近刺针的分区和被刺穿的部分以内的所有正负极活性物质同时反应的功率。

传热方面的理论基础主要是传热学的相关理论，须考虑分区模块之间和模块与环境之间的传热。利用集总参数的方法，将分区内的温度简化为统一的温度。此外，单体比热容cp根据式(7)计算，最大取1 200J·kg-1·℃-1；固体与空气的对流换热系数h取值范围一般在5～10W·m-2·℃-1之间，因为仿真的是电池在开放空间中的针刺过程，对流换热强度较高，所以取h=10W·m-2·℃-1；电池壳表面不锈钢的辐射系数ε视表面的氧化程度在0.075～0.85间取值，因认为电池壳氧化程度较低，所以取ε=0.1；电池单体内的传热系数λ，选取沿电池厚度方向的传热系数为38.54W·m-2·℃-1。

每个分区的能量守恒方程为

cpmΔT=Q副反应+Q焦耳+Q正负极+Q传热

(10)

式中：cp为分区比热容；m为分区质量；T为分区温度；Q副反应为分区热失控副反应释放的热量；Q焦耳为分区针刺短路产生的焦耳热；Q正负极为隔膜解体后分区正负极活性物质直接反应释放的热量；Q传热为该分区与接触分区和周围环境交换的热量。对应的微分方程为

(11)

4 模型预测与实验结果的对比

4.1 针刺热失控实验

针刺实验在特制的针刺挤压实验台架进行。特制的装有热电偶的刺针安装在穿刺夹具上，实验时以20mm/s的固定速率刺入SOC为100%的电池单体中。

实验中，在单体内的中间面1，2，3，4位置处(图11)和刺针上布置了热电偶，以测量单体温度的变化和分布规律。

实验时，当刺针一刺入单体时，立刻发生少量的液体喷溅，并瞬间产生明火(图12)。

图13是实验中测得的单体中间平面上的温度变化曲线。针刺后热失控迅速发生，针刺后36s时，在位置3上出现最高温度762.6℃。

图14是针刺后最初10s的温度曲线。从图中可以看出，位置1的温度(以下简称T1)最先开始上升，之后其他位置的温度开始上升。位置2、位置3的温度(以下分别简称为T2，T3)最终超过T1。刺针的温度(以下简称Tn)上升较慢并且远低于其他位置的温度。

图15是单体针刺的温度曲线和电压曲线。从图上可以看出，当刺针刚刺入单体时电压就开始下降，并且当T1超过210℃左右时降为0。T1在针刺1s后开始上升。最初10s的电压、温度变化十分迅速，但由于数据记录仪采样频率的限制，最初10s的曲线并不光滑。

4.2 模型预测结果

在Matbab/Simulink针刺热失控模型并进行仿真。

图16是仿真得到的针刺过程温度曲线。由图可见，针刺后温度瞬间上升并发生热失控，热失控后17s时，在位置3上出现最高温度837.8℃。

图17是针刺后最初10s的温度曲线。由图可见，T1最先开始上升，之后其他几个电池分区的温度开始迅速上升，并超过T1。

图18是仿真得到的温度电压变化曲线。由图可见，电压在2s内降低到0，温度在针刺最初就开始上升。

4.3 仿真结果与实验结果的对比

对比4.1节中的单体针刺实验结果和4.2节中的模型预测结果，可以发现以下共同点：

(1) 单体的急剧温升阶段均持续了3s左右；

(2) 电压在针刺开始后2s均降为0；

(3) 均是与刺针相邻的区域温度最先开始升高，之后其他区域的温度才开始升高并超过与刺针相邻区域的温度；

(4) 最高温度出现的位置相近，实验中为位置3，模型中最高温度出现在位置3和相邻的位置2与位置4(3个位置温度差别较小)；

(5) 热失控结束后的单体降温速度基本一致。

但是模型预测的结果与实验结果也有不同之处。模型预测结果与实验结果的差异及产生原因作如下简要分析。

(1) 模型中的最高温度837.8℃高于实验的762.6℃。该差异产生的原因应该是：热失控副反应使用的单位体积卷层中反应物质量Wc，Wp，WPVDF，We直接取自文献，而文献研究的18650电池与本研究使用的电池型号不同，在电池配料的比例方面会有差异，而且模型中用整个电池单体的体积替代了卷层体积，因此这些参数须针对研究使用的电池单体重新折算。

(2) 模型中最高温度的出现时间与实验中最高温度的出现时间有差异，模型中为17s,实验中为36s。造成该差异的原因应该是模型中简化了隔膜失效的过程。模型中当触发温度达到电压突降对应温度时，隔膜失效，电化学能瞬间释放，即各分区隔膜失效的时刻是相同的。但实际过程中，当某部分隔膜达到电压突降对应温度时，该部分隔膜失效，即各部分隔膜失效的时刻不同。

(3) 模型中预测的Tn远高于实验得到的Tn。这是因为模型中将刺针当作了一个孤立物体，而且取得长度较小；实际上刺针长度较大，且连接在针刺/挤压实验台架上，与台架之间的接触换热迅速。

(4) 模型中电池单体的温升从针刺入时就开始发生，而实验中电池的温升大约在针刺后1s才发生。产生该差异的原因，可能是模型中没有考虑刺针刺入速度的影响，而实际中刺针是以20mm/s的速度刺入电池的，该过程正好需要1s多的时间。

(5) 模型中各分区的温度差异没有实验当中明显。造成该问题的原因，应该是对模型的外部换热因素考虑得不够全面，比如夹持电池单体的石棉与钢板，单体上方产生的明火和喷出的气体。

5 结论

本文中主要研究了三元锂离子动力电池的热失控现象，设计并进行了HPPC实验、热箱加热热失控实验和针刺热失控实验，并基于热失控副反应理论以及通过实验测得的电池参数和性能规律，建立了电池单体的针刺模型并进行了仿真研究。

首先，利用HPPC实验对实验电池的性能和一致性进行了评估，保证了后续实验结果的可比性和有效性，并获取了常温下实验电池电压、内阻随SOC的变化规律。

其次，通过热箱加热热失控实验，对三元锂离子动力电池在绝热条件下的热失控现象进行了分析。获得了实验电池的电压突降点温度、热失控点温度和热失控最高温度等特征数据。并得到了实验电池20～240℃范围内的电压随温度的变化规律，和25～180℃范围内的内阻随温度的变化规律。

之后，利用实验得到的数据和规律，以及热失控副反应动力学方程等理论模型，在Matlab/Simulink环境下搭建了单体的针刺模型。该模型耦合了热失控副反应、焦耳热、传热3方面的因素。

仿真结果与针刺实验得到结果较为吻合，急剧升温时长、压降时刻、温升规律、温度分布规律和散热速率等几乎一致。这说明建模的思路是合理的，并且也说明利用集总参数法进行针刺过程仿真是有效的。

仿真结果表明：(1)在针刺过程中，热失控现象主要是由刺针引起的短路生热、穿刺区域的正负极物质的电化学反应放热这两个条件所共同触发的；(2)电池单体的电化学能，主要通过隔膜失效后的正负极活性物质直接反应而瞬间释放，短路电流消耗的电化学能只占很小的比例。

该模型与实际情况吻合度较高，对于后续的机理研究和系统开发工作具有参考价值，对锂离子动力电池三维建模具有指导作用。通过对模型的细化和完善，还可进一步提高模型的精度。

[1] 刘潇潇,漆文辉,黎曦,等.电动汽车及其发展趋势分析[J].湖南电力,2010,30(5):59-62.

[2] 刘光明.纯电动汽车电池管理系统开发及SOC估计算法研究[D].北京:清华大学,2010.

[3] 陈清泉,孙立清.电动汽车的现状和发展趋势[J].科技导报,2005,23(4):24-28.

[4] 何鹏林,乔月.锂离子电池热滥用试验研究[J].安全与电磁兼容,2010(4).

[5] Venugopal G. Characterization of Thermal Cut-off Mechanisms in Prismatic Lithium-ion Batteries[J]. Journal of Power Sources,2001,101(2):231-237.

[6] Balakrishnan P G, Ramesh R, Prem Kumar T. Safety Mechanisms in Lithium-ion Batteries[J]. Journal of Power Sources,2006,155(2):401-414.

[7] Kim G H, Pesaran A, Spotnitz R. A Three-dimensional Thermal Abuse Model for Lithium-ion Cells[J]. Journal of Power Sources,2007,170(2):476-489.

[8] 李腾,林成涛,陈全世.锂离子电池热模型研究进展[J].电源技术,2009,33(10):927-932.

[9] Hatchard T D, MacNeil D D, Basu A, et al. Thermal Model of Cylindrical and Prismatic Lithium-ion Cells[J]. Journal of the Electrochemical Society,2001,148(7):A755-A761.

[10] Spotnitz R, Franklin J. Abuse Behavior of High-power, Lithium-ion Cells[J]. Journal of Power Sources,2003,113(1):81-100.

[11] Bandhauer T M, Garimella S, Fuller T F. A Critical Review of Thermal Issues in Lithium-ion Batteries[J]. Journal of Electrochemical Society,2011,158(3):1-25.

[12] Biensan P, Simon B, Peres J P, et al. On Safety of Lithium-ion Cells[J]. Journal of Power Sources,1999,81-82:906-912.

[13] Wang H Y, Tang A D, Huang K L. Oxygen Evolution in Overcharged LixNi1/3Co1/3Mn1/3O2 Electrode and Its Thermal Analysis Kinetics[J]. Chinese Journal of Chemistry,2011,29:1583-1588.

[14] Kim H, Kong M, Kim K, et al. Effect of Carbon Coating on LiNi1/3Mn1/3Co1/3O2 Cathode Material for Lithium Secondary Batteries[J]. Journal of Power Sources,2007,171:917-921.

[15] Kim H, Kim K, Moon S I, et al. A Study on Carbon-coated LiNi1/3Mn1/3Co1/3O2 Cathode Material for Lithium Secondary Batteries[J]. Journal of the Solid State Electrochemistry,2008,12:867-872.

[16] Smith K, Kim G H, Darcy E, et al. Thermal/electrical Modeling for Abuse-Tolerant Design of Lithium Ion Modules[J]. International Journal of Energy Research,2010,34(2):204-215.

[17] Yamauchi T, Mizushima K, Satoh Y, et al. Development of a Simulator for Both Property and Safety of a Lithium Secondary Battery[J]. Journal of Power Sources,2004,136(1):99-107.

Experiments and Modeling of Nail PenetrationThermal Runaway in a NCM Li-ion Power Battery

Zhang Mingxuan1, Feng Xuning1, Ouyang Minggao1, Lu Languang1, Wang Fang2& Fan Bin2

1.TsinghuaUniversity,StateKeyLaboratoryofAutomotiveEnergyandSafety,Beijing100084;2.LaboratoryofNewEnergy,ChinaAutomotiveTechnology&ResearchCenter,Tianjin300300

Aiming at a hidden safety issue, i.e. thermal runaway phenomenon, happening in the Li-ion power battery of pure electric vehicle, the process of one of most violent thermal runaway, i.e. that with nail penetration in a NCM Li-ion power battery is studied in this paper. Based on hybrid pulse power characteristic (HPPC) test, oven heating thermal runaway test and existing models, a lumped parameter model describing the process of nail penetration thermal runaway is built with corresponding experiments conducted. The prediction results with the model are validated by experiments. This lays a foundation for subsequent research and system development.

NCM Li-ion power battery; nail penetration thermal runaway; experiments; modeling

*科技部国际科技合作计划(2011AA11A269)、教育部国际科技合作计划(2012DFA81190)、北京市科技计划与国家支撑计划(Z121100007912001,2013BAG16B01)和清华大学自主科研课题(2011Z01004)资助。

原稿收到日期为2013年11月6日，修改稿收到日期为2014年2月16日。