四轴车辆全轮转向之自动模式研究*
2015-04-12陈思忠郑凯锋
陈思忠,郑凯锋
(1.北京理工大学机械与车辆学院,北京 100081; 2.中国北方车辆研究所,北京 100072)
2015143
四轴车辆全轮转向之自动模式研究*
陈思忠,郑凯锋
(1.北京理工大学机械与车辆学院,北京 100081; 2.中国北方车辆研究所,北京 100072)
在第2轴转角比例于第1轴转角,第3轴转角比例于第4轴转角的条件下,从理论上分析了全轮转向与双前桥转向之间的差异。接着以质心侧偏角为零,设计了控制器一和控制器二两种控制器,并再次分析了双前桥转向、带控制器一的全轮转向和带控制器二的全轮转向三者之间的区别与联系,为四轴车辆的全轮转向技术的研究提供了理论参考。
四轴车辆;全轮转向;自动模式
前言
随着四轴车辆在重型货车和军用战术型车辆上的广泛应用,轮胎磨损严重、转弯半径大和操纵稳定性差等问题愈加突显。全轮转向技术可谓是解决这些问题的最佳方案。为充分发挥全轮转向的优势,四轴车辆的全轮转向至少应具有4种模式,分别是最小转弯半径模式(MinR)、蟹行模式(Crab)、传统模式也称双前桥转向模式(F4ws)和自动模式(Auto),如图1所示。MinR模式下后两桥与前两桥呈逆向转向,适用于车辆的大角度转弯或调头;Crab模式下后两桥与前两桥同向转向,适用车辆的横向移位或爬横坡。前两种模式仅适用于低速行驶,而F4ws和Auto模式则适用于整个车速范围。其中,F4ws模式下,后两桥不转向,它是一种安全模式,当控制器掉电或损坏、传感器失效等发生时都将触发此模式;Auto模式可以根据车速和车辆状态调节成前后逆向转向或前后同向转向,以达到改善低速时的机动性和高速时的操纵稳定性的目的。在较多研究中表明以零质心侧偏角设计Auto模式的控制器有很好的性能[1-2],但多数是针对两轴或三轴车设计的,对四轴车研究较少。另外,所设计的控制多以仿真为主,缺乏理论分析。本文中侧重于理论分析,研究双前桥转向、以第1轴转角和车速为输入及以稳态零质心侧偏角为目标的全轮转向控制器一和在控制器一的基础上增加横摆角速度反馈形成的控制器二这三者之间的区别与联系。
1 四轴车辆的全轮转向基本特性
1.1 双前桥转向(F4ws模式)
保留原有四轴车辆的双前桥转向传动机构,在第3和第4桥添置电控液压转向系统,可最容易地实现四轴车辆的全轮转向。合理地设计双前桥转向传动机构可使前两轴的车轮都绕同一转向中心转向,同时,在转角20°内,可保证第1轴车轮的转角与第2轴车轮的转角成比例关系[3]。同前两轴一样,可设定第3轴转角与第4轴转角也成比例关系,这样既方便了对控制器的设计也有助于对全轮转向特性的理论分析。在以上假设条件下,四轴车辆的线性2自由度模型[4]可写为
(1)
其中
(2)
式中:m为整车质量;u为车辆纵向速度;Li为整车质心到第i轴的距离(此距离具有方向性,与行车方向一致为正,反之为负);Ci为第i轴的轮胎侧偏刚度(左、右轮胎刚度之和);Iz为整车的横摆转动惯量;β为质心侧偏角;r为横摆角速度;δi为第i轴中间虚拟车轮转角,简称第i轴转角;δ2=d1δ1;δ3=d2δ4;d1,d2为大于零小于1的常数。
对式(1)进行Laplace变换并化简可得
(3)
(4)
其中
(5)
对P1进行分析,可知
(6)
式中um定义为转折速度:
(7)
当选择F4ws模式时,即令δ4=0,车辆的稳态质心侧偏角和稳态横摆角速度分别为
(8)
(9)
式(9)中广义轴距[4]可写为
lm=P1/P3
(10)
广义的不足转向系数[4]可写为
K=-Cbm/P3
(11)
显然,K的正负取决于Cb。当Cb>0时,K<0,车辆在F4ws转向模式下属于过多转向,当Cb<0时,K>0,属于不足转向;当Cb=0时,K=0,属于中性转向。车辆在F4ws模式下应具有适当的不足转向,以保证行驶的稳定性,即应保证Cb<0。
1.2 全轮转向
以上讨论了F4ws模式下的基本特性,下面讨论Auto模式的情况,并与F4ws模式作对比。Auto模式下车辆的稳态质心侧偏角为
(12)
两种模式下的稳态质心侧偏角之差为
Eβ=|β(s)|Auto,s=0|-|β(s)|F4ws,s=0|=
(|P1δ1(s)+P2δ4(s)|-|P1δ1(s)|)/P0
(13)
Auto模式下的稳态横摆角速度为
(14)
两种模式下的稳态横摆角速度之差为
(15)
由式(13)~式(15)可知,当u≤um且δ1δ4<0时,有Eβ≤0,Er≥0;当u≥um且δ1δ4>0,有Eβ≤0,Er≤0。即当车速小于转折车速,后两桥输入与前两桥逆向转向时,可减小车辆的质心侧偏角,增大稳态横摆角速度;当车速大于转折车速,后两桥输入与前两桥同向转向时,可减小车辆的质心侧偏角,同时降低横摆角速度。此特性不因控制算法不同而改变,反映了以式(1)为基础设计Auto模式下的控制器时,全轮转向的本质特性。
2 全轮转向Auto模式控制器设计
2.1 控制器一(Auto-Con1)
根据式(12),以稳态零质心侧偏角为目标设计第4轴转角可得
(16)
式(16)给出的控制器满足了车辆在转折车速前实现逆向转向,转折车速后实现同向转向,使低速和高速时质心侧偏角都减小。
将控制器式(16)经过Laplace变换后分别代入式(3)和式(4),可得质心侧偏角和横摆角速度对第1轴转角的闭环传递函数为
(17)
(18)
其中
P5=(L1C1+d1L2C2)(C4+d2C3)-
(L4C4+d2L3C3)(C1+d1C2)>0
(19)
由式(18)可知稳态时的横摆角速度为
(20)
令式(18)等号右边分式的分母为零,对其求解即可分析车辆采用控制器一时系统的稳定性。对比式(17)、式(18)与式(3)、式(4)可见,在控制器一作用下,F4ws模式与Auto模式下控制器一具有相同的特征多项式,说明控制器一的加入并未改变系统的稳定性。
2.2 控制器二(Auto-Con2)
控制器一实际上以车速和第1轴转角作为变量计算第4轴的转角,并未考虑车辆的状态;在此基础上增加横摆角速度反馈,则成为控制器二。
将式(1)的质心侧偏角微分方程重写为
(21)
令式(21)的质心侧偏角及其变化率为零,则可得第4轴转角为
(22)
将控制器式(22)代入式(1)原车辆方程并进行Laplace变换,可得质心侧偏角和横摆角速度对第1轴转角的闭环传递函数为
(23)
(24)
其中
(25)
根据式(24)可知稳态时横摆角速度为
(26)
将式(26)代入式(22)可得稳态时第4轴转角为
(27)
对比式(26)和式(20)可以看出,稳态时控制器二和控制器一的横摆角速度相等,其原因由式(27)与式(16)可知,稳态时控制器二的第4轴转角输出与控制器一的相同。因此,以质心侧偏角为零设计出的具有反馈横摆角速度的控制器二与不具备反馈横摆角速度的控制器一在稳态转向时的效果一致,不同之处在于瞬态过程。控制器二在瞬态时具有尽量保持有较小的质心侧偏角的能力,而控制器一没有。另外,控制器二改变了系统的特征根。表1为车辆参数,以此车特性参数进行仿真分析。
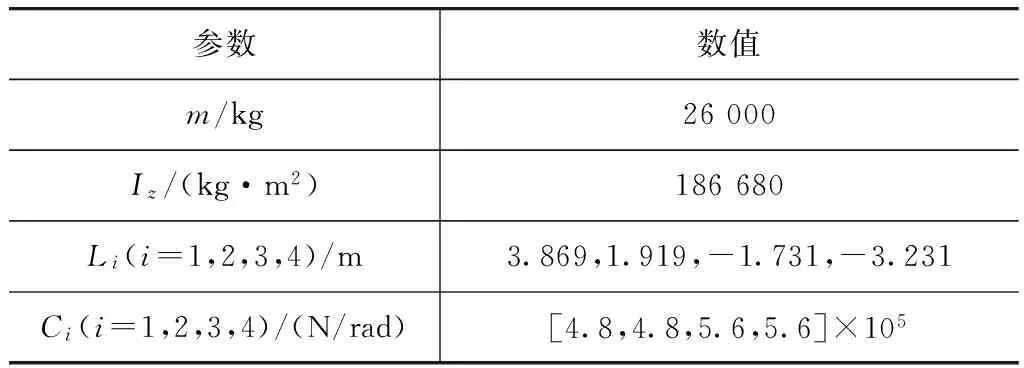
表1 车辆参数
图2为以车速为参变量绘制的特征根曲线图,用以对比两种控制下特征根的特性。
从图2中可以看出,由控制器一和控制器二分别组成的闭环系统的两个特征根s1和s2都在负半轴,即系统是稳定的。对于控制器一,在低速时,具有两个负实根,在高速时,具有一对共轭复根,即当车速从低速增至高速时,车辆由过阻尼系统转变为欠阻尼系统。而对于控制器二,车辆一直处于过阻尼状态。
3 Auto模式下稳态分析
在稳态时,控制器一与控制器二的第4轴转角和横摆角速度相同。在此,以车速和第1轴转角为变量,代入车辆参数分析第4轴转角和稳态横摆角速度的变化特性,仿真结果如图3和图4所示。
从图3可以看出,随着车速的增加,第4轴由与第1轴逆向转向逐渐转变为与第1轴同向转向,其转折车速为51km/h。从图4中可以看出,在转折车速前,Auto模式下的稳态横摆角速度要大于F4ws模式下的稳态横摆角速度,即驾驶员以相同的横摆角速度进行转弯时,Auto模式下驾驶员对转向盘的输入转角要比F4ws时小,降低了驾驶员的操作强度;在转折车速后,情况正好相反,即驾驶员须多打转向盘来完成转向,这样提高了车辆的行驶稳定性。另外,从图3和图4中可以看出,处于转折车速时,第4轴转角为零,相应的横摆角速度相等。从式(7)中可以看出,当车辆特性参数给定时,容易改变的参数是d1,它与转折车速的关系如图5所示。
从图5中可以看出,d1从0变化到1.0时,转折车速接近线性地由46km/h上升到53km/h。另外,从实际情况考虑,d1的设计要考虑轮胎磨损且受限于安装空间,其可变范围很小。所以,当车辆特性参数确定后,其转折车速基本可以确定。
4 Auto模式下瞬态分析
稳态分析考查了车速与第4轴转角和横摆角速度的关系。对于瞬态过程可以从固有频率、阻尼比和反应时间来研究。
首先研究F4ws模式下的瞬态特性。将式(4)进行Laplace反变换,并且令第4轴转角为零,可得F4ws模式下横摆角速度的2阶振动微分方程为
(28)
第1轴角阶跃输入时,其转角的数学表达式为
(29)
当t>0时,式(28)可简化为
(30)
其中固有频率ω0和阻尼比ζ为
(31)
(32)
式(30)是一个2阶常系数非齐次微分方程,它的通解由一个特解和所对应齐次微分方程的通解组成,因此它的通解可以写为
(33)
其中
(34)
式中:A0为特解;A1,A2,A3,A4,A5,A6都是积分常数,可以根据运动的初始条件来确定。角阶跃输入下的初始条件可写为
(35)
结合初始条件和通解方程可求出相应的积分常数,求解过程在此省略,各积分常数表述如下:
(36)
(37)
A3=-A0
(38)
A4=r0-ω0A0
(39)
(40)
(41)
采用角阶跃输入,横摆角速度第一次到达稳态值A0所需的时间为反应时间τ,但也可以取到达稳态值0.95A0的时间作为反应时间。此处取到达95%稳态值所对应的时间。即当t=τ时,将r(τ)=0.95A0代入式(33)可得
(42)
若令0.05A0=0,可推导出到达100%稳态时的反应时间的公式,而当0.05A0≠0时,式(42)为超越方程,可进行数值求解。
接下来分析采用控制器一时的瞬态特性。将式(18)进行Laplace反变换,可得到Auto模式采用控制器一时横摆角速度的2阶振动微分方程为
(43)
同理,采用零时刻角阶跃输入时可以将式(43)简化为
(44)
式中的ω0和ζ仍然是式(31)和式(32)所表达的固有频率和阻尼比,说明控制器一的加入并不改变车辆的固有频率和阻尼比。但反应时间会因特解和初值的不同有所变化。此时的特解变为
(45)
零时刻下的横摆角速度初值变为
(46)
由式(45)给出的特解和式(46)给出的横摆角速度初值,仍然可用式(42)求出采用控制器一时的横摆角速度到达95%稳态值的反应时间。
最后考查采用控制器二时的瞬态响应。将式(24)进行Laplace反变换可得到采用控制器二时横摆角速度的2阶振动微分方程为
(47)
同理,采用零时刻角阶跃输入时可将式(47)简化为
(48)
其中固有频率ω0和阻尼比ζ变为
(49)
(50)
可见控制器二改变了车辆的固有频率和阻尼比。此时的特解和横摆角速度初值也变为
(51)
(52)
同样,将式(51)和式(52)代入式(42)便可求解出采用控制器二时横摆角速度到达95%稳态值的反应时间。限于篇幅,对瞬态特性不进行仿真分析。
5 结论
当前两轴和后两轴分别成比例转向时可便于Auto模式控制器的设计和理论分析。以减小质心侧偏角为目标,转折车速便是前、后逆向转向和同向转向的分界线,并且一旦车辆特性参数确定后,此转折车速也便确定。在前面假设的基础上,设计了两种控制器,从理论和仿真两方面对双前桥转向、采用控制器一的全轮转向和采用控制器二的全轮转向作了对比分析。结果表明,双前桥转向与采用控制器一的全轮转向具有相同的系统特征根、固有频率和阻尼比,而控制器一与控制器二具有相同的稳态第4轴转角输出和稳态横摆角速度。
[1] Bayar K, Unlusoy Y S. Steering Strategies for Multi-axle Vehicles[J]. International Journal of Heavy Vehicle Systems,2008,15:208-236.
[2] Watanabe K, Yamakawa J, Tanaka M, et al. Turing Characteristics of Multi-axle Vehicles[J]. Journal of Terramechanics,2007,44:81-87.
[3] 王定华,李龙银.一种载货车双前桥转向机构的设计[J].合肥工业大学学报(自然科学版),2007,30:73-76.
[4] Williams D E. Generalised Multi-axle Vehicle Handling. Vehicle System Dynamics[J].2012,50(1):149-166.
A Research on the Automatic Mode of All-wheel Steering for Four-axle Vehicle
Chen Sizhong1& Zheng Kaifeng2
1.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081; 2.ChinaNorthVehicleResearchInstitute,Beijing100072
Under the condition of that the wheel turning angles in second and third axles are respectively proportional to those of first and fourth axles, the differences between all wheel steering and double-front-axle steering are analyzed theoretically. Then with the sideslip angle of mass center set to zero, controller 1 and controller 2 are designed, and the differences and connections between double-front-axle steering, all wheel steering with controller 1 and all wheel steering with controller 2 are analyzed again, providing theoretical references for the research on the all wheel steering technique for four-axle vehicle.
four-axle vehicle; all-wheel steering; automatic mode
*工业和信息化部项目(C2220061355)资助。
原稿收到日期为2012年11月12日,修改稿收到日期为2013年3月20日。
