聚焦错误本源，寻找改进对策——三年级学生万以内数加、减法计算错误成因分析及对策

浙江新昌县南明小学（312500） 毛裕浩

万以内数的加减法是整数计算教学中的核心内容，它以20以内数的加法、减法为基础，尤其是进位加法和退位减法，这些加减法计算的正确率和熟练程度直接影响万以内数加、减法的正确率和熟练程度，而万以内数的加减法又是后续学习的小数加、减法，多位数乘两位数，小数乘除法等内容的基础，足见这一内容的重要性。

一、分析教材学情，统计错误现象

从计算的角度思考，万以内数的加法、减法的算法可以分为三个步骤：一是相同数位上的数字相加减；二是从个位算起；三是分为两种情况：加法是哪一位上的数字相加满十，就向前一位进1，减法是哪一位上的数字不够减，就向前一位退一做十，相加后再减。这三个步骤学生口头表达已非常清晰，但具体运用第三个时却是差强人意。

从教材呈现的内容分析，万以内数的加减法可以分为加法和减法两大块。加法可以细分为：A．三位数加三位数出现一次进位（可以是任何数位相加满十）；B．三位数加三位数出现两次进位（可以是任意的两个数位相加满十）；C．三位数加三位数出现三次进位。减法可以细分为：a．三位数减两位数或者三位数，个位不够减出现一次退位；b．三位数减两位数或者三位数，个位、十位不够减，出现两次退位，被减数中间、末尾都没有0；c．三位数减两位数或者三位数，个位、十位不够减，出现两次退位，被减数中间、末尾都有0；d．三位数减两位数或者三位数，个位、十位不够减，出现两次退位，被减数中间有0，末尾没有0。

根据这些分类对学生的计算易错题进行调查统计，结果如下。

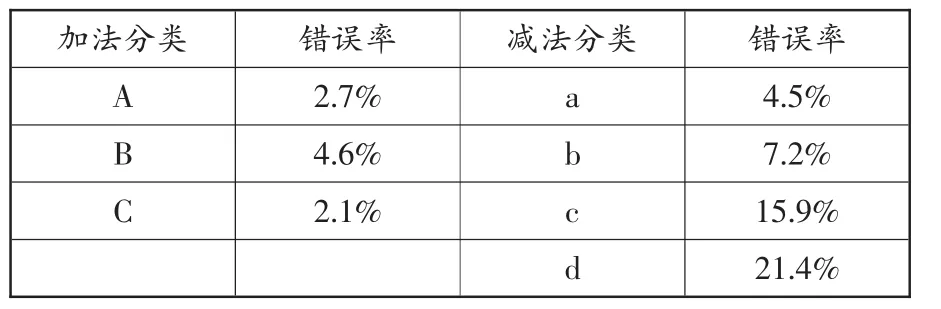
加法分类 错误率 减法分类 错误率A 2．7% a 4．5%B 4．6% b 7．2%C 2．1% c 15．9%d 21．4%

二、分析统计数据，聚焦错误本源

总体分析：根据以上的统计数据我们发现，学生的计算易错题总体上归类为：①减法计算错误率高于加法计算错误率（尤其退位减法比进位加法错误率要高）。②十位、百位计算错误率要高于个位计算错误率。③计算习惯不好的学生的错误率要高于计算习惯好的学生的错误率。如常有学生忘加进上来的1，忘减退位的1。

阶段性分析：在加法计算中，第一阶段的一次进位学生不太会出现错误，而遇到连续进位后学生出错的情况明显增多，主要是对20以内数的进位加法和十几加1的加法不够熟练造成的。在减法计算中，学生对于第一阶段的一次退位容易记住要减掉退位的1，而遇到连续退位，尤其是“被减数中间有0的情况，个位不够减，向十位退1，十位不能退1，先要向百位退1，再从十位退1”的情况学生较难理解，尤其是一些学困生。

三、分析典型易错题，寻找改进对策

学生在数学学习的过程中经常出现错误，错误并不可怕，它是学生经历了分析、对比、理解、调整等学习方式后对问题的一种反馈。那么，万以内加减法中的哪些计算题是学生难以掌握、容易犯错的呢？我搜集了大量的学生作业，对学生的错误进行了调查、访谈与思考，归纳整理出了以下几种错误类型。

类型一：个位倒着减

◆典型错题

◆错因分析

这两道计算题都出错在个位。针对这样的错误，我对学生进行了访谈。

【访谈一】

师：你能说说412－269得数的个位是怎么算出7的？

生：我是先从个位算起，个位的2－9不能减，那我就倒过来变成9－2了。

师：2－9是不能减还是不够减？

生：我听同学说是不能减。

师：9－2 够减吗？

生：够。

师：那2－9够减吗？

生：不够减。

师：2－9不够减怎么办？

生：向十位借1再减。

……

【访谈二】

师：你能说说803－320得数的个位怎么算出是7的？

生：不好意思！老师，我看错了，应该是3。

……

从学生的访谈中，我找到了错误的原因：

1．学生在平常的减法计算中接触最多的是被减数比减数大或者被减数和减数相等，也就是够减的情况，因此碰到被减数比减数小即“不够减”的式子，学生的第一反应是认为没有这样的减法式子，是“不能减”的，即做不了，“不能减”那就倒回来减，两种减法的结果是一样的，这和加法式子将两个加数交换位置后再加结果不变是一样的。

2．万以内数的减法主要是学习“不够减需要退位”的减法，经过大量具体式子的练习，学生头脑中浮现“不够减”的减法已盖过了以前所学“够减”的减法，受头脑中“不够减”的强势影响，把“够减的”也当成“不够减”的了。

3．加法交换率的负迁移。在加法计算中如2＋9和9＋2的结果是一样的，学生认为减法9－2和2－9的结果也是一样的。

◆改进策略

1．规范数学语言。“不能减”和“不够减”虽一字之差，但意思差别很大。“不能减”是减法中的两个数字不能参与减法计算，不存在减法式子，而“不够减”是被减数比减数要小。根据学生的学习心理和接受新事物的特点，学生（尤其是学困生）对“不够减”的减法式子外观上还不能很快接受，觉得很别扭。为此，在教学中，应先从心理上让学生尽快接受这样的减法式子，让学生清楚这样的减法式子属于“不够减”，不是“不能减”，在这之前碰到的减法都属于“够减”。特别注意的是，在做这样的减法时要规范使用“不够减”这一数学语言。

2．加强对比练习。个位倒着减中，错误最多的是类似“0－3”这样的减法，很多学生看到后都会不假思索直接写出答案“3”。为此在基本的口算练习中设计一组对比口算题：3－0，0－3，10－3，让学生在计算中比较“3－0，0－3”这两题的区别，比较“0－3，10－3”这两题的关系。在比较中发现前两题的被减数和减数交换了位置，结果是不相等的，这和“3＋0，0＋3”是有区别的；而后两题是第一题不够减了要退位后再减（变成第二题了）的关系。在多次比较计算中学生就能够明白“够减”可以直接减，“不够减”需要退1后再减，从而理解减法计算的基本算理。

类型二：个位计算正确，十位或百位计算错误

◆典型错题

◆错因分析

这些错误中个位都计算正确，而十位或百位都出现计算错误，归纳起来有以下几种：（1）加法。①个位数字相加未满10，却向十位进1；②十位相加满10，却未向百位进1。（2）减法。①个位不够减向十位借1，没点退位点，十位忘了退1；②个位不够减，向十位借1，标有退位点，却没有退1。归结这些错误原因，主要有：①算理不清。相加满10没有进1，进1了却没有加上去；不够减没有退1，退1了却没有减掉。从学生的竖式计算看，没有进1标记和退位点标记的比有此类标记的错误率更高。②数字显性和隐性的影响。个位上的数字计算相对其他数位是显性的，可以直接进行加减，而其他数位上的数字相加减还存在着一些隐性因素，如进上来的1，退1后的数字已经不是原来的数字了，但变化后的数字没有直接呈现在学生眼前，需要学生有很强的辨别能力，并时刻注意数字的变化，为此相对于个位，其他数位计算错误较多。

◆改进策略

1．注重加减法算法的指导。随便找一个学生让他说万以内加减法的计算算理，他会说得很清楚，但会说不一定会应用。尤其是相加满10要向前一位进1时，总是把进上来的1漏加；遇到不够减向前一位退1时，总是忘了退1。这类现象看似简单，其实是学生不清楚算理。学生只看到了竖式中显性的数字，对显性的数字会直接相加减，而隐性的数字变化却未能及时发现并让其参与计算。为此，在竖式计算的初期要求学生说出每一步的计算过程，尤其是遇到相加满10进1和不够减退1的情况，将这一计算算理熟练化，以达到熟练计算的技能目标。如计算“689＋346”时，引导学生说出“9＋6 等于 15，写 5 进 1，8＋4 等于 12，12＋1 等于 13，写 3 进 1，6＋3 等于9，9＋1等于10，直接写10（这一步不要再写0进1了，防止出现类似“931＋785＝716，百位相加满10向千位进1的 1没有写下来的错误”）”。计算“412－269”时，要求学生说出：“2－9不够减，向十位退1，并在十位的数字上点上退位点，12－9＝3，0－6 不够减向百位退 1，在百位数字上点上退位点，10－6＝4，3－2＝1。”在口算时也要求学生把这些计算步骤说完整。

2．关注加减法计算的习惯。学生在计算加法时，知道相加满十了，向前一位进1的1往往不写，记在脑子中再计算；做减法时需要退1的数字不做退位标记，凭记忆去计算。从学生错误情况分析，有“进1”和退位标记的学生比没有做标记的学生的错误率要低。从刺激学生注意的角度思考，所做的标记能给计算起到提醒的作用，不做标记则要对学生的注意力有要求，要求能够把不存在的数字清晰地存在脑子中并参与运算。为此，要求学生计算进位加法和退位减法时标出“进1”和退位标记，并使之成为一种做题习惯。

类型三：同一竖式加减混淆

◆典型错题

◆错因分析

错误的原因是个位上的数字用加法计算，其他数位上的数字用减法计算，在同一个竖式中出现了两种运算。若题目中个位出现6和8，学生算错的可能性较大。我结合学生的访谈和自己的思考，归纳出以下原因：①学生的日常生活经验影响。中国的传统习惯认为6和8是代表吉祥的数字，在商品价格、车辆牌照、吉日选择等方面尽可能用上6和8这两个数，这样学生在生活中接触较多的也是6和8这两个数。②计算出现的顺序影响。在计算教学的教材编排中，首先出现的是加法，如先有6＋8＝14，再有相关的减法出现，学生对第一次出现的事物接受和存储迅速且记忆长久。③隐藏数字未及时显现的影响。个位6＋8是显性的加法，直接计算出和即可，而个位的6－8，被减数隐藏着变化情况16，其实是16－8，相比较直接计算6＋8，难度加大了。

◆改进策略

1．积极验算核对。验算是检验计算结果正确与否的一种有效方式，前提是参与计算的数字和符号要抄正确。在平时的验算中可以根据需要写出完整的验算过程，一般情况下，加法可以用减法验算，减法可以用加法验算，也可以验算结果的个位，这是一种快速检验计算结果正确与否的方式，通过验算个位正确与否来判定整个计算是否正确，从而去发现、纠正原先的计算错误。

2．强化对比练习。如同时出现546－168和546＋168这样两道题，先让学生观察相同点和不同点，在计算的不同中真正体会到同样的数字用不同的运算得出的结果是不同的，而在同一个竖式中一种运算一直到底，不会加减掺杂其中。让学生也编写一些类似的计算题进行练习，在强化对比中进一步体会计算的不同。

心理学家桑代克认为：“尝试与错误是学习的基本形式。”的确，在数学学习的过程中，学生犯错是一种学习的积累与挑战，教师要允许学生犯错，错误是一种很好的教学资源，但关键是如何引导学生认识到自己的错误，找到自己数学学习上的纰漏，并能吸取教训使自己下次不再犯错或少犯错误。计算教学的实践与思考还有很多路要走，在实践中还会面对学生各种各样的错误，但错误有错误的精彩与价值，让我们聚焦错误的本源，寻找有效的改进策略。