数形结合让计算教学走向深刻——以“小数乘小数”教学为例

江苏南京市长江路小学（210018） 李 勤

数形结合是小学数学中常用的、重要的一种数学思想方法。数形结合思想的实质即通过数形之间的相互转化，通过形象化的方法，转化为适当的图形，从而直观地发现数量之间存在的内在联系。以数助形，以形助数，教师恰当渗透数形结合的思想，能够帮助学生明晰算理，掌握算法。在新一轮的课程改革中，不仅要给学生授之以“鱼”，更要授之以“渔”，数形结合思想所表现出来的思路上的灵活，过程上的简便，不仅能帮助学生学习抽象的数学知识，开拓解题思路，更能有效地培养学生创造性的思维，为学生今后的学习打下坚实的基础。笔者以”小数乘小数”为例，剖析数形结合思想在计算教学中的具体应用，以期能揭示“数”与“形”之间的相互转换的紧密关系，提高学生的思维品质。

【教学片段】

投影出示小研究

《小数乘小数》小研究右图是小明房间的平面图。你能算出他的房间面积是多少平方米吗？我的算式：我的计算方法：3．8 米米．82

师：会列式吗？

生：3．8×2．8。

师：先自己尝试算一算。再把你的想法和小组同学说一说。

生1：把 3．8 看成 38，2．8 看成 28，38乘8等于304，38乘2等于76。一位小数乘一位小数，得数也是一位小数。得数是 106．4。

生2：不可能是 106．4，因为估算一下 3点几乘2点几不可能得到100多。

师：估算的方法可以帮助我们判断计算是否正确。

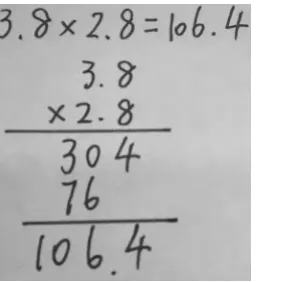
生3：先算个位8乘8等于64，再算十位3乘2等于6。两次计算的结果相加，得数是12．4。

生4：12．4也不可能，3点几乘2点几最多不会超过4×3，得数应该比12小。

生5：我也是先想 38 乘 28，把 3．8 和 2．8 都同时扩大了10倍。计算得数是1064，刚才是每个数都扩大了10倍，相乘也就是扩大了100倍，所以得数要缩小100倍，就是 10．64。

师：她的算法大家听明白了吗？这样一来，原来的小数乘小数就转化成了——

生：整数乘整数。

师：怎么得到304的？

生6：38 乘 8 得到 304。

师：你们又是怎么理解76的？

生7：其实这个76是760，是38乘20得到的。

师：10．64是从哪里冒出来的呢？

生8：因为把 3．8 变成了 38，2．8 变成了 28，分别都乘10，得数是1064后，就要把刚才“×10”给还原回去，刚才分别乘了两个10，所以我们要把小数点向左移动两位。得数就是10．64了。

师：我们再来看看，3．8米等于多少分米？2．8米等于多少分米？

生9：3．8＝38 分米，2．8 米等于 28 分米。师出示一个长方形：

师：这个长方形的长是38分米，宽是28分米。38相当于30＋8，28相当于20＋8，那么可以把长方形分成下面这样的四块。想一想，先算什么？

生10（生边说，边在图中画出计算出的部分）：28中的8和38中的8相乘。

然后8再和38中的30相乘。（生在图中表示出来）

接着算20分别和8、30相乘。（生继续涂色表示）

师：把几次相乘的结果相加，我们看得数是多少？

生：64＋240＋160＋600＝1064 平方分米，就是 10．64 平方米。

师：刚才通过算38分米×28分米得出结果，想一想3．8 米×2．8 米的算理和它一样吗？

生：一样的。

生11：先算 2．8 中的 0．8 分别和 3．8 中的 0．8 与 3 相乘，再算2乘0．8和3，就能计算出得数。。

师：解释得真清楚。那么，回到之前，想一想有同学得到106．4是怎么回事？

生1：我是当成 38 乘 2．8 了。

师：再看 12．4，这个 12．4 是怎么算出来的？

生3：我看图已经明白了，我算的12．4，其实只算了0．8 乘 0．8 和 3 乘 2 的这两块。

……

“小数乘小数“教学，教师常会结合竖式计算分析讲解算理，但小学生的思维以直观形象思维为主，而算理、算法又十分抽象，因此如何结合学生的思维特点处理好运算教学中算理与算法的关系，往往就是教学的难点所在。在以上的教学中，让学生经历了从具体到抽象、从感性到理性的过程，并能让学生用自己语言表达出其中的道理。可以看到，通过画图演示，学生能直观感知两个数相乘的过程，因为数形结合让这一道理一目了然。

【反思】

一、渗透数形结合思想，深刻理解算理

学生学习、理解和掌握“数的运算”内容时都要经过从具体到抽象、从感性到理性的过程，这就需要教师在教学的过程中不仅要关注结果、关注方法，还要关注得到结果、得到方法的思维过程，这个思维过程就是学生理解算理、掌握算法的过程。算理的抽象和算法的直观形成了鲜明的对比，在低年级计算教学中，教师通常用小棒、计数器等各种学具来组织学生的学习活动，从而把算理形象化、具体化，而到了高年级，抽象的逻辑思维成了大多数学生的思维特点，此时，学具的应用逐渐由符号、示意图及空间想象等方式代替。数形结合的思想则帮助学生清晰每一步算的是什么，明白这样计算的道理在哪里，有效沟通新旧知识之间的联系，形成知识串。

二、渗透转化思想，巧妙掌握算法

小学数学“数与代数”领域的很多运算都可以通过转化将其分解成简单运算或已学过的运算来解决。解读教材，新知的学习以旧知为台阶，只有找到了新旧知识的内在联系，找准新知生长点，勇于探索，就能探寻出解决新问题的新方法，数形结合的思想方法，也体现了转化的思想，为沟通新旧知识搭建桥梁。

三、通过数形结合，加强对数学知识的记忆

对于学生来说，计算比较枯燥单调，算理抽象难懂。数形结合能使抽象的计算学习尽可能形象化，可以帮助学生形象地理解和记忆。

数形结合既是一个重要的数学思想，又是一种常用的数学方法，这种“数”与“形”的信息转换，相互渗透，不仅可以帮助学生学习新知，同时还可以大大开拓解题思路，为研究和探求数学问题开辟了一条重要的途径。在数学教学中教师要有意识地沟通数、形之间的联系，帮助学生逐步树立起数形相结合的观点，提高学生主动运用的意识，并使这一观点扎根到学生的认知结构中去，从而提高学生的数学修养与解题能力。