基于多重分形的大型风力机主轴故障诊断

刘 欢，王 健，高淑芝，郭 烁，张琳琳

(沈阳化工大学，辽宁 沈阳 110142)

0 前言

大型风力机由于其运行工况复杂、环境恶劣、保养周期长、维修成本高，要求风力机的机械系统具有较高的可靠性。在大型风力机的各组成部件中，在国内现有风场中有相当一些省份的气流阵风因子比较强，风力机的主轴长时间处在比较复杂的载荷激励作用下高效运转，经常超负荷工作，超过该风力机设计的极限标准，及其容易出现故障。所以，当风力机故障被发现时，已经晚了，只能被拆卸到地面，进行诊断修理，会使风力机维修成本大增，影响该企业的效益。因此对风力机主轴工作状态进行监测就显得非常必要［1］。因此，及时有效地对大型风力机的滚动轴承进行状态监测和故障诊断，对保证风力机健康安全地运行，提高风力机的运行寿命具有十分重要的意义［2］。

1970 年分形理论被提出，分形理论中的研究对象是现实生活中和自然界中广泛存在的几何形态，该几何形态的特征是非规则的，具有自相似的形态。

分形理论也是对较为复杂多元化信息系统问题的处理方法之一，效果是明显的。本文通过对大型风力机主轴振动时域信号，进行相空间重构，同时对风力机主轴振动信号的多重分形谱进行分析，以及分析风力机主轴系统工作状态等。最后提出了基于多重分形方法的一种大型风力机主轴早期故障诊断的新方法，其测试对象是吉林某风场大型风力机组，功率是1.5 WM，通过分析其测试试验的结果，可以得出利用分形理论方法对大型风力机主轴系统进行初期的故障诊断，效果很好，给其它大型机械设备的诊断提供借鉴。

1 多重分形分析

由于大型风力发电机动力特性非常复杂，其主轴的振动信号容易出现混沌的特性，所以很难对风力机建立动力特性的数学模型。混沌系统是复杂的，其中分形理论与混沌系统又具有非常密切的关系，混沌行为的有用工具是分形几何，对于非线性系统来说，分形维数是表示混沌系统的一个特征量和定量参数［3］。混沌运动的奇怪吸引子或者轨道都是分形，同时分形理论也是用一个谱函数对不同层次的特征的描述。混沌行为的混乱性和高度无序通过反映在分形的复杂性上面。其中对于风力机主轴额振动信号特征描述完全可以通过信息维数、盒维数和关联维数等分形理论方法来描述。

以上这些方法在机械故障诊断中已经有证实。其中多重分形在定义分形理论上，是指几个标度指数的奇异测度所组合成的集合体。但是如果要描述风力机主轴振动时域的图谱的分形维数时，它是单一的。其整体特征的标度指数不是很细致的［4］。

考虑了系统的局部行为以及分形体在成型过程中不同层次特征。

公式中αi是表征分形体某小区域的分维，又叫做局部分维，它的数值大小表示某个区域内生成概率的数值;公式中的Pi是表示分形理论总体生长界面在该区域内的生长概率的数值;公式中Li是表示该区域内线度数值。因为这样的区域数量较多，所以公式中的αi能够组合成无穷多个分形序列谱，其中多重分形用字母α 和f(α)来表示。因此，在现场试验中或者在工程中字母Pi不是那么容易被测量出。所以，应该利用统计物理学中的一些高效表示方法对公式(1)概率加权求和计算得到

利用不同标度分形来描述风力机主轴振动信号在不同层上的不均匀随机概率分布，根据奇异谱α－f(α)来寻找和发现多标度分形特征。通过这些多标度分形变化对兆瓦级风力发电机组主轴的工作状态进行诊断识别，由此判断主轴故障的类型，降低风力发电机事故的发生几率。

在吉林某个风场，利用传感器采集同一型号风机主轴的信号，风机功率是1.5 MW，风机的采样频率均为2 kHz。其中，设任意一台风力发电机机组时间序列为{xk，k=1，2，……N}，把该时间序列放入到m 维欧几里得空间Rm中，可以求得一个集合，该集合表达式如下

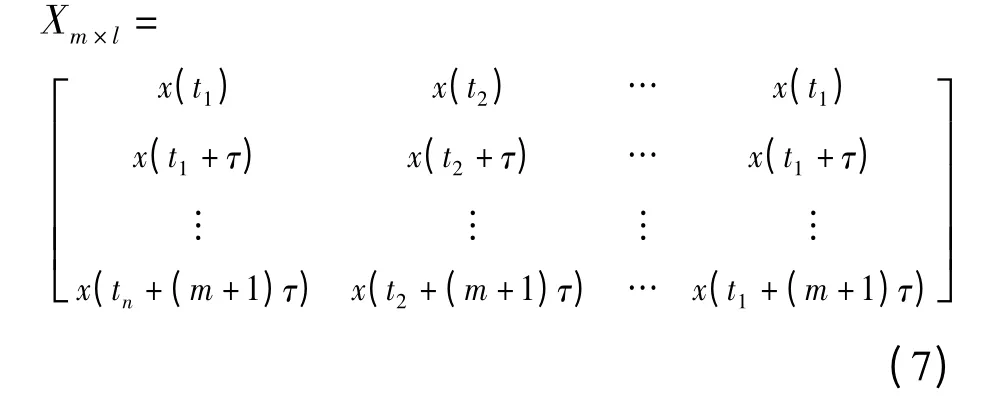
其中该集合的嵌入维数是由能够包含状态转移构成的吸引子的最小空间维数构成。随着在时间序列的相空间重构过程中，Tackcns 证明了嵌入空间维数的嵌入定理，表达式如下

其中公式中m 表示嵌入空间的维数;公式中DA表示原状态空间吸引子所处空间的维数。通常选择的嵌入维数数值大于20，因此可以稳定其关联维数的数值，在本文中选择m 的数值为25。因此计算对矩阵Xm×l中任意两点之间的距离表达式如下所示。

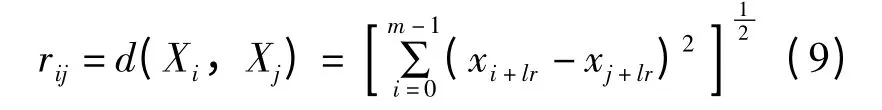
k×k 阶的矩阵R 由所有空间矢量之间的距离组成，因此就可以定义q 阶关联积分表达式如下所示。

公式中的字母H 是表示Heabiside 函数。时间序列多重分形广义维数谱可以通过，{yk，k=1，2，…N}分别是q 阶关联积分计算得到如下表达式

通过选择数值不同的q 值，就能够计算得到其对应的广义维数Dq，通过上面的结果就可以辨别出异常设备和正常设备的信号状态特征向量。从而能够判断出故障。

2 基于多重分形的故障诊断研究

吉林某风场1.5 MW 大型风力机于2012 年底投入运行，正常运行不到一年，2013 年9 月工作人员发现该风电机组有明显的不正常振动现象，经过现场勘察发现，引起该振动的主要来源是给发电机冷却用的轴流风机运行时发出的，因此同年10 月对该风电机组的轴流风机两侧的振动信号进行了数据采集。现场试验采用的是德国生产的普卢福VIBXPERT 测试传感器，FFT 信号分析仪和数据采集器。振动信号的时域波形图和包络谱分别如图1 和2 所示。

图1 三个传感器采集到信号的时域波形图Fig.1 Time-domain waveform of vibration signals

从图2 可以看出，采集到的各个信号的包络信号频率出现混叠，无法分辨滚动轴承真正的振动信号，这对滚动轴承的故障诊断极为不利。为了提取滚动轴承的故障信息，采用多重分形算法对采集到的信号进行分离，分离结果分别如图3所示。

图2 三个传感器采集到信号的包络图Fig.2 Envolope spectrum of three vibration signals

图3 采用多重分形算法分离的信号包络谱图Fig.3 Separation of signal envelope spectrum with multi-fractal method

从图3 中可以清晰地看出第一个频谱图可以看出滚动轴承故障频率64 Hz 及其倍频成分，三个分离信号依次为滚动轴承故障信号、电机转频信号和随机干扰信号，分离结果相当明显，说明采用多重分形算法提高了分离精度和分离的可靠性。

3 结论

针对大型风力机主轴的振动特性，采用多重分形算法对吉林某风场大型风力机的实测数据进行分离。仿真结果表明，该方法可有效分离大型风力机主轴与轴流风机的振动信号，有助于大型风力机复杂动力特性状态的早期识别。

［1］Y.Amirat，M.E.H.Benbouzid.A brief status on condition monitoring and fault diagnosis in wind energy conversion systems［J］.Renewable and Sustainable Energy Reviews.2009，13(9):2629－2636.

［2］S.J.Watson，B.J.Xiang，W.Yang，P.J.Tavner，等.Condition Monitoring of the Power Output of Wind Turbine Generators Using Wavelets［J］.IEEE Transactions on Energy Conversion.2010，25(3):715－720.

［3］董广明，陈进.基于循环频率能量的滚动轴承损伤程度识别［J］.振动工程学报，2010，23(3):249－253.

［4］王晓冬，何正嘉，訾艳阳.多小波自适应构造方法及滚动轴承复合故障诊断研究［J］.振动工程学报，2010，23(4):438－444.

［5］Junyan Yang，Youyun Zhang，Yongsheng Zhu.Intelligent fault diagnosis of rolling element bearing based on SVMs and fractal dimension［J］.Mechanical Sys-tems and Signal Processing.2007，21 (5):2012－2024.

［6］S.J.Watson，B.J.Xiang，W.Yang，P.J.Tavner.Condition Monitoring of the Power Output of Wind Turbine Generators Using Wavelets［J］.IEEE Transactions on Energy Conversion.2010，25(3):715－720.

［7］M.J.Roan，J.G..Erling，L.H.Sibul.A new non-linear adaptive blind source separation approach to gear tooth failure detection and analysis［J］.Mechanical Systems and Signal Processing.2007(16):719－740.

［8］Parra L，Spence C.Convolutive Blind Separation of Non-stationary Sources［J］.IEEE Trans.On Speech and Audio Processing，2000，8(3):320－327.

［9］B.E.Parker.Fault Diagnostics Using Statistical Change Detection in the Bispectral Domain［J］.Mechanical Systems and Signal Processing.2000(14):561－570.