自适应EEMD 法提取大型风机主轴承早期故障特征

张 磊，陈长征，刘 杰

(1.沈阳工业大学机械工程学院 沈阳 110870)

0 前言

风力发电作为一种主要的可再生能源，近年来发展迅猛［1］，但对于其运行状态的监测与故障诊断仍缺乏有效的方法［2］。风力发电机主轴承的振动信号是非线性、非平稳的，而且早期故障信号往往十分微弱，容易被背景噪声掩盖，因此需要一个行之有效的信号处理方法［3］。汤宝平［4］等人将Morlet 小波变换分别与Wigner-Vile分布相结合，有效地提高了信噪比并抑制了Wigner-Vile 分布交叉项的产生，该方法能够很好地提取出故障特征。随后，汤宝平［5］等人使用Morlet 小波变换与奇异值分解相结合的复合算法，该算法能够很好地提取出振动信号中的冲击特征。訾艳阳［6］等人提出多小波驱动块阈值降噪的方法，在风力发电机早期故障诊断中取得了良好的效果。陈长征［7］等人将小波分析理论引入到大型风力发电机主轴承的故障特征中，有效地提取出了主轴承的早期故障。Norden E.Huang提出的基于EMD 法的希尔伯特变换，是分析非线性、非稳态信号的有力工具［8］。陈文静［9］使用基于EMD 的Hilbert 变换，诊断风力发电机主轴承的故障。EMD 算法具有自适应性，但由于算法本身的缺陷，存在着模态混叠的现象。为了克服这一问题，Wu Z H 等人提出了基于白噪声的总体平均经验模态分解(EEMD)［10］。该算法比较好地解决了模态混叠的问题。Amitat［11］等人使用EEMD 算法，通过分析发电机定子电流进行风力发电机组发电机滚动轴承的故障诊断。EEMD 算法的分解效果依赖于所添加的白噪声的方差σ 与总体平均次数N，而这两个参数需要根据经验人为添加。

本文针对风力发电机主轴承振动信号，设计仿真信号进行仿真实验，分析参数σ 与N 取值与模态混叠抑制情况的关系，得出σ 与N 的自适应取值准则。随后，使用实测信号对仿真实验所得出的自适应取值准则进行验证。

1 自适应EEMD 法

1.1 EEMD 分解

EEMD 的步骤如下:

(1)向原始信号x(k)中N 次添加均值为0、标准差为σ 的白噪声ni(k)，即

式中，ni(k)为第i 次加入的白噪声;xi(k)为第i 次加入白噪声后的信号。

(2)对每个xi(k)分别进行EMD 分解，其具体算法可参考文献［4］，分解得到的各个IMF 分别记为cij(k)，余项为ri(k)。

(3)将分解得到的对应的IMF 进行总体平均运算，得到EEMD 的分解结果，即

式中，cj(k)为信号x(k)经EEMD 分解后所得到的第j 个IMF;r(k)为余项。

由此可以看出，影响EEMD 分解效果的首要因素便是σ 与N 值的选取。从已搜索的论文来看，使用EEMD 法进行机械振动信号处理时，σ 与N 主要是根据经验人为选取，并不具有自适应性。

1.2 σ 的自适应选取

为了研究添加白噪声标准差σ 与分解精度的关系，针对实测大型风力发电机主轴承位移信号，设计了仿真实验。

(1)设置仿真信号。

式中，A1=5～50 μm;f1=10～20 Hz;φ1=0～2π;A2=400～600 μm;f2=0.1～0.4 Hz;φ2=0～2π;n(k)=－10～5 dB。

(2)计算Sig(k)的标准差σn。

(3)对信号Sig(k)进行EEMD 分解，取添加的白噪声标准差σ=v·σn，其中v=0.025 ∶0.025 ∶ 0.5。

(4)找出与s1(k)相对应的IMF，计算其相关系数，以相关系数为评价指标，统计相关系数最大时所对应的v 值。

此次仿真实验共计算了200 个仿真信号，EEMD 分解精度与v 的关系如图1 所示。

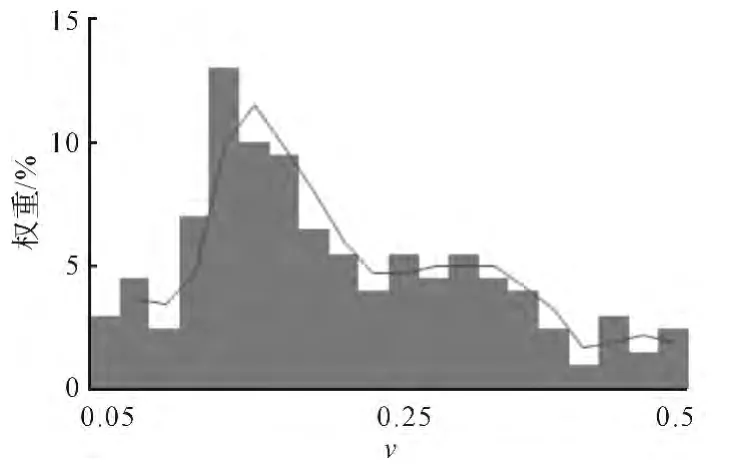
图1 v 与EEMD 分解精度Fig.1 Relationship between v and EEMD

从图1 中可以看出，当v 取值为0.1～0.2时，便能够有效抑制模态混叠现象，获得较高的分解精度。在此，取v=0.15。

1.3 N 的选取

由于EEMD 算法向原信号中添加了白噪声，因而会使分解结果产生一定的误差。通过增加整体平均次数N，可以有效地抑制由于添加的白噪声所引起的误差。文献［12］中给出了整体平均次数N 的取值规则:

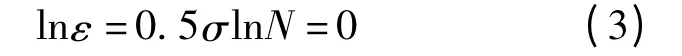
式中，N为整体平均次数;ε为最终可接受误差的标准差;σ为所添加的白噪声的标准差。

通过上文自适应取得σ，便可确定整体平均次数N 的取值。

2 实例分析

本文数据采集自内蒙古赛汉风场风机主轴承径向位移信号，如图2 所示。7#风机(CCWE-1500/70.DF)存在潜在故障，主轴转速为12 r/min。采集主轴承径向位移信号，采样频率为1024 Hz，采样时间为10 s。8#风机(CCWE-1500/70.DF)运行正常，主轴转速为14.4 r/min。采集主轴承径向位移信号，采样频率为1024 Hz，采样时间为10 s。

根据轴承的参数以及主轴的转速，可以计算出每种故障所对应的特征频率［11］。由于风机主轴承的转速很低，因此主轴承故障的特征频率也集中在低频带上。但如图2 所示的实测振动信号，由于存在很强的低频干扰，一般的信号处理方法很难从振动信号中提取出故障特征。

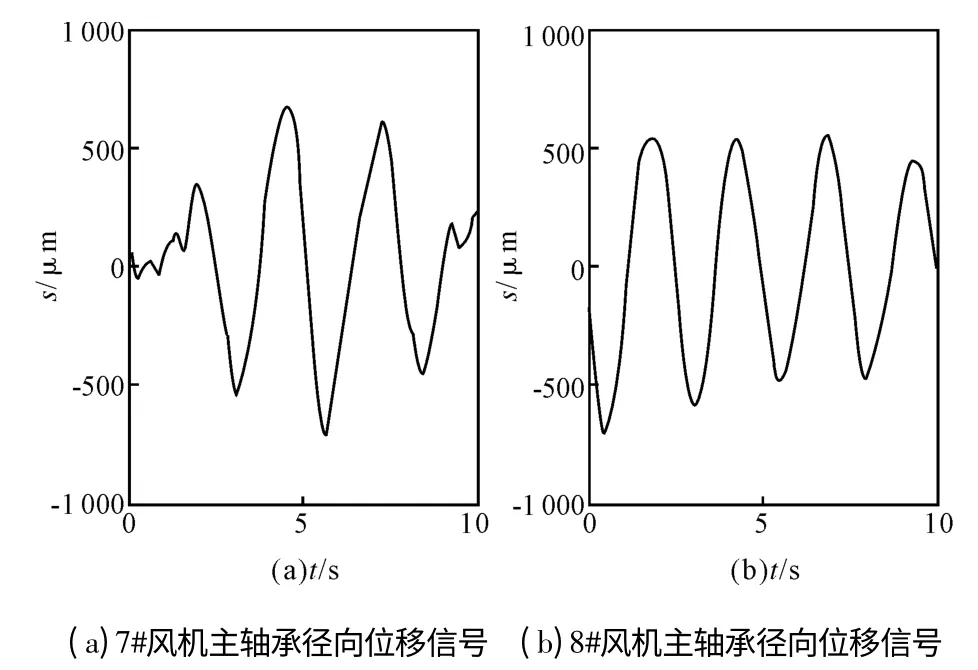
图2 风机主轴承径向位移信号Fig.2 Radial displacement signal of wind turbine main bearing

使用自适应EEMD 分别对7#风机、8#风机位移信号进行分解。由于轴承的故障信号主要为冲击信号，计算7#风机信号自适应EEMD 分解结果的峭度谱，选择故障特征所在的IMF。峭度谱如图3 所示(不包含余项)。

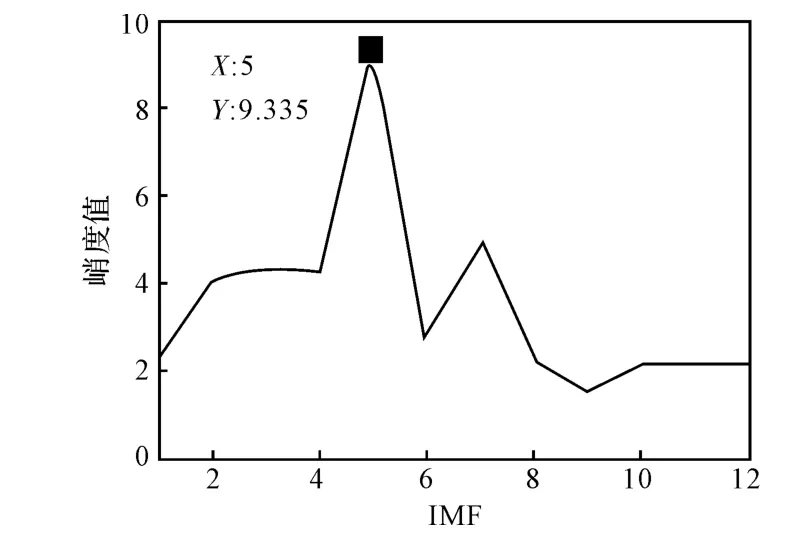
图3 7#风机自适应EEMD 分解结果峭度谱Fig.3 Kurtosis spectrum of 7# wind turbine with self-adaptation EEMD

峭度值大于4 时，信号有明显的冲击特性。从图3 中我们可以看出，IMF5 的峭度值为9.34，说明IMF5 中包含明显的冲击信号，IMF5 中可能包含风机的故障特征，因此提取IMF5 进行进一步分析。提取IMF5，其时域信号如图4a 所示。虽然，从图中可以看出一定的周期性，但是仍然很难从时域信号中直接得出有用的结论。对时域信号进行傅里叶变换，将IMF5 转化到频域上，其频谱如图4b 所示。同时，对8#风机振动信号进行自适应EEMD 分解，相近频带的IMF为IMF4，其时域与频域分别如图4c、图4d 所示。

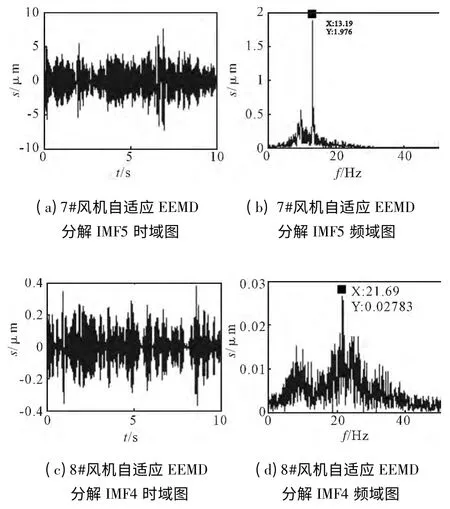
图4 时域和频域图Fig.4 Time and frequency domain of IMF5 and IMF4

从图4b 中可以看出，存在一个频率为13.19 Hz、幅值为1.98 μm 的值信号。而图4d中显示的正常运行的8#风机主轴承在这一带宽上的振动幅值较小，最大值不超过0.03 μm，说明7#主轴承存在一定的早期故障。文献［13］中指出了滚动轴承各故障特征频率的计算方法。通过计算，该频率与外圈故障特征频率相接近，因此可以初步判定，7#风机主轴承存在早期的外圈故障。

分析研究自适应EEMD 在模态混叠抑制上的效果。分别使用EMD、v=0.05 的EEMD、v=0.25 的EEMD 与自适应EEMD 对7#风机振动信号进行分解，取上文所示频带及其相邻频带，计算其频谱，计算结果如图5 所示。

从图5 中可以看出，无论是EMD 分解、v=0.05 的EEMD 分解、v=0.25 的EEMD 分解还是自适应EEMD 分解，均提取出了13.19 Hz 这一故障特征，但在模态混叠的抑制上有着不同的效果。图5a 所示，EMD 法提取出的13.19 Hz 处的峰值在幅值上最大，但其IMF5 与IMF4 有大量的重叠，存在着较严重的模态混叠现象。如图5b 所示，其在13.19 Hz 处的峰值略小于EMD 算法分解出的结果。从定性的角度来说，其IMF6与IMF5 的重叠程度与图5a 所示的EMD 分解相比，并无明显的抑制效果，但计算13.19 Hz 处IMF5 与IMF6(图5a 计算IMF4 与IMF5)的比值，v=0.05 的EEMD 分解的比值为2.49，而EMD分解的比值为2.19。由此可见，与EMD 分解相比，v=0.05 的EEMD 分解在模态混叠上有一定的抑制效果。图5c为v=0.25 的EEMD 分解，已呈现出明显的白噪声特性，效果较差。图5d中，各个IMF 分量表现出了一定的白噪声特性，但仍在可接受范围之内。从定性的角度来说，模态混叠得到了一定程度的抑制。计算其13.19 Hz处IMF5 与IMF6 的比值，比值为2.64，由此可见，在抑制模态混叠上，自适应EEMD 分解有着更好的效果。

图5 不同方法对模态混叠抑制效果的对比Fig.5 Contrast on inhibition effect of mode mixing with different methods

3 结论

针对实测出的大型风力发电机主轴承的振动信号，设计仿真实验，研究了EEMD 分解参数添加白噪声标准差σ 的取值与抑制模态混叠现象效果之间的关系。对仿真实验结果的统计表明，当v 取0.1～0.2 时，EEMD 算法对模态混叠现象会有较好的抑制效果，本文中取σ=0.15进行进一步研究。总体平均次数N 的选取，应遵循lnε+0.5σlnN=0。因此，只要给出最终可接受误差的标准差ε，便可自适应地获取参数σ与N。

根据仿真实验得到的自适应取值准则，建立自适应EEMD 算法，使用该算法对实测信号进行分析并比较不同算法的分解效果。通过内蒙古赛汉风场7#、8#风机主轴承振动信号的实例分析，证明自适应EEMD 算法可以有效地提取大型风力发电机主轴承振动信号的故障特征，且该算法在抑制模态混叠现象方面的效果要优于EMD 算法与一般EEMD 算法。因此，自适应EEMD 算法可以作为一种前处理算法，应用于大型风力发电机主轴承的状态监测与故障特征提取。

［1］Kiviluoma J，Meibom P.Influence of wind power，plug-in electric vehicles，and heat storages on power system investments［J］.Energy，2010，35(3):1244－1255.

［2］陈雪峰，李继猛，程航，等.风力发电机状态监测和故障诊断技术的研究与进展［J］.机械工程学报，2011，47(9):45－52.

［3］Su W，Wang F，Zhu H，et al.Rolling element bearing faults diagnosis based on optimal Morlet wavelet filter and autocorrelation enhancement［J］.Mechanical Systems and Signal Processing，2010，24(5):1458－1472.

［4］Tang B，Liu W，Song T.Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution［J］.Renewable Energy，2010，35(12):2862－2866.

［5］Jiang Y，Tang B，Qin Y，et al.Feature extraction method of wind turbine based on adaptive Morlet wavelet and SVD［J］.Renewable energy，2011，36(8):2146－2153.

［6］Sun H，Zi Y，He Z.Wind turbine fault detection using multiwavelet denoising with the data-driven block threshold［J］.Applied Acoustics，2014，77(6):122－129.

［7］Chen C，Sun X，Gu Q，et al.Wavelet-based multifractal analysis of large scale wind turbine main bearing［J］.Journal of Renewable and Sustainable Energy，2013，5(1).

［8］Lei Y，Lin J，He Z，et al.A review on empirical mode decomposition in fault diagnosis of rotating machinery［J］.Mechanical Systems and Signal Processing，2012.

［9］陈文静，吴金强.Hilbert-Huang 变换在风力发电机主轴轴承故障诊断中的应用［J］.轴承，2013 (6):59－62.

［10］Wu Z，Huang N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method［J］.Advances in adaptive data analysis，2009，1(01):1－41.

［11］Amirat Y，Choqueuse V，Benbouzid M.EEMD-based wind turbine bearing failure detection using the generator stator current homopolar component［J］.Mechanical Systems and Signal Processing，2013，41(1):667－678.

［12］Randall R B，Antoni J.Rolling element bearing diagnostics—A tutorial［J］.Mechanical Systems and Signal Processing，2011，25(2):485－520.2004，460(2046):1597－1611.