上证综指收益率波动的预测研究

李 聪 刘诗绮 张伟伟

（青岛大学　经济学院，山东　青岛　266071）



上证综指收益率波动的预测研究

李 聪 刘诗绮 张伟伟

（青岛大学经济学院，山东青岛266071）

摘 要：股票市场巨大震荡表明要保持金融市场平稳健康的运行，必须重视资产风险管理工作，股票指数波动影响着经济社会的发展。因此，对股票市场收益率波动的研究就显得尤为重要。本文以上证综合指数为研究对象，结合上证指数收益率统计特征，引入GARCH模型对股票指数收益率波动性进行分析预测。研究结果表明GARCH模型对上证综合指数收益率波动性有着较好的拟合、预测效果。

关键词：股指收益率； 波动预测； GARCH模型

一、 引言及述评

在我国，随着资本市场改革的愈发完善和股票开户政策的进一步放开，越来越多的投资者将资金投入股市，以期望获得更大的投资回报。2015年6月，我国沪深两市日最高交易金额已突破1万亿。一方面，资金大量流入股市增加了股票市场的流动性，也优化了投资者的投资组合；另一方面，当前中小投资者的风险管理意识和相关金融知识储备参差不齐，进一步放大了股票市场的投资风险。2015年7月以来，我国股票市场遭遇史无前例的股灾，上证综指在短短一个多月时间从5178.19断崖式跌至2850.71，最大跌幅达到44.9%，中小投资者甚至部分风控良好的投资机构损失惨重，因此，加强股票市场的风险管控势在必行。而股票市场收益率的波动正是反映股票市场投资风险的“温度计”，对于市场波动率的预测不仅对投资者管控投资风险有着重要的意义，对于短期经济预警也具有一定的现实意义。在我国，上证综指是股票市场上最具代表性的指数，其波动最能反映股票市场的整体运行状况[1]。GARCH模型在预测波动性数据的分析和预测上的适用性高于其他模型，而且股票指数的统计特征和波动性特点恰恰符合GARCH模型的基本假设。因此，基于GARCH模型对我国股票市场波动性进行分析预测具有较强的科学性和适用性[2]。

在目前神经网络的应用中，绝大部分学者使用BP神经网络进行瓦斯涌出量方面的预测[1]，但是BP网络在函数逼近时采用扶梯度下降法进行权值调节，这种方法存在收敛速度慢和局部极小的缺点[2]。

对于股票市场收益率波动性的研究兴起于20世纪60年代，早期的学者大多采用传统时间序列模型，以收益率为被解释变量，以时间变量为被解释变量进行研究分析。但是，由于收益率波动性的统计特性，传统计量经济学的统计方法在预测精度上差强人意。1982年，R.F.Engle创造性的提出了ARCH模型，开创了时间序列数据波动性分析的先河。随后，研究学者大力发展了ARCH模型并提出了相关的衍生模型[3]；Pagan（1986）以金融资产收益率时间序列数据为研究对象，从统计学角度对数据进行了统计特征分析，研究结果表明，金融资产收益率时间序列数据具有尖峰厚尾、均值回归、波动相关等特性，奠定了ARCH及其衍生模型分析预测股市收益率波动的理论基础[4]；Bollerselv （1988）和Taylor（1986）系统分析了ARCH模型无法预测残差序列函数长期自相关的缺陷，并进一步提出GARCH模型，针对股票市场收益率时间序列数据的尖峰厚尾分布统计特征进行了分析，达到了较好的预测效果，该方法的提出为金融市场的资产管理和资产风险控制领域做出了巨大贡献[5]。之后，Pagan（1986）也采用了该方法对金融资产收益率进行统计特征研究。目前，基于GARCH模型的实证研究已逐渐成为分析我国资本市场收益率的主流方法。龚锐（2005）运用GARCH族模型对中国股市价值风险做出了深入的比较分析，研究结果表明，GARCH模型在股票市场具有普适性[6]；李文君（2009）从数学角度对GARCH模型进行了综合性的研究述评，他认为，只要保证一些关键变量的数理特征，GARCH模型对实证数据就有着优秀的拟合预测精度；刘志东（2010）通过对多元GARCH模型的结构特征进行分析，系统总结了GARCH模型的历史理论研究成果，并从理论层面证实了GARCH模型可以被运用到金融市场的相关实证问题研究，进一步巩固了GARCH模型金融市场研究的理论基础[7]；马超群等（2011）利用外汇期货交易数据，通过引入Kendall秩相关系数结合Copula-GARCH模型计算外汇期货的最优套期保值比率，实证结果表明，研究所使用的方法结合GARCH模型进行套期保值能显著降低交易成本，有效规避外汇风险[8]；王辉（2011）基于ADCCGARCH模型进行了进一步修正提出了修正ADCCGARCH模型，对我国商品期货市场动态套期保值进行了实证研究，研究结果表明，我国商品期货价格和现货价格的对数存在协整关系，另外，研究准确的测算了中国商品期货的最优套期保值比率[9]；王天一等（2014）运用修正Realized GARCH模型结合传统GARCH模型对沪深300指数高频交易数据进行了实证研究，研究结果表明，传统GARCH模型和Realized GARCH模型在波动率预测方面都有较高的预测精度[10]；魏红燕（2014）根据短期汇率市场波动性特征，将GARCH模型应用于短期汇率预测中得到了较好的预测效果[11]。近年来，GARCH模型得到了极大的发展，并且根据不同的假设条件衍生出了GJR，EGARCH，GARCH-M等模型，但从实证研究的发展来看，GARCH模型对于收益率波动性的预测和拟合有着更好的准确性和普适性.因此，本文拟采用GARCH模型对我国股票市场上证综指的收益率波动性进行研究。

二、 理论模型

以股票市场个股为例，构造简化GARCH模型：假定股票在第t天的收盘价格为，则股票收益率的计算公式为：

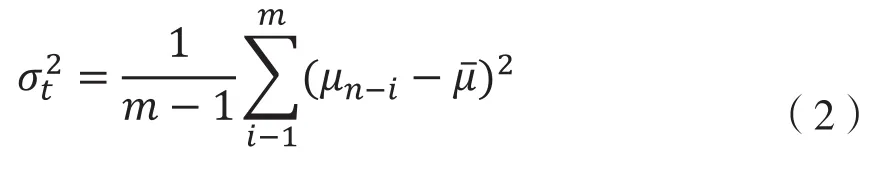
其中，

近年来，绿色环保成为包括印刷行业在内的诸多行业都在谈及的话题，实则于上海新星而言，践行绿色环保的行动早已开始。按照徐毛清的理解，做环保，就要达到真正的绿色，而就上海新星而言，则从两方面着手，即生产过程和最终产品。

郭文安：教材编写往往被人看成是对学科基础知识的编排与阐述，对有关科研成果的概括和整理，因而不受重视，甚至不被看作是一种科学研究。教材编写与科学研究确有所区别，前者主要是在已有科研成果基础上进行的。但是，二者亦有共同点，教材编写同样具有探索、研究、整合与创新的属性，实质上也是一种科学研究。因为一本好的教材应有广博、坚实、精深的专业知识。它不应限于概括与整理已有的科研成果，在学科理论的简明化、系统化和体系化上都应有新的突破、发展与提高。它应兼具专业性、基础性、学术性和前瞻性。它可使广大师生及读者受益匪浅，获得进一步探究的依据与动力。可以说，一本好教材其价值并不亚于一本好专著。

（二）GARCH模型拟合预测

（一）样本数据统计特征

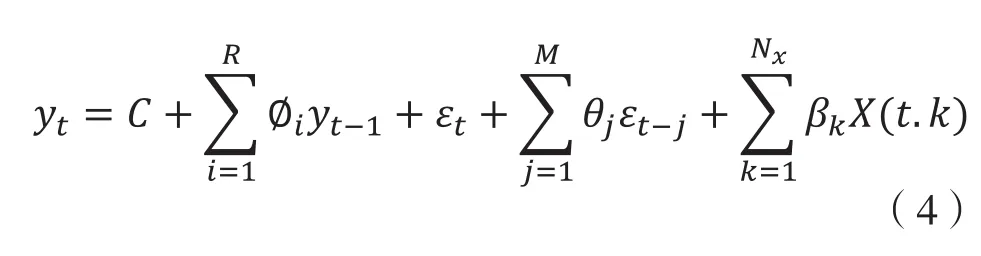
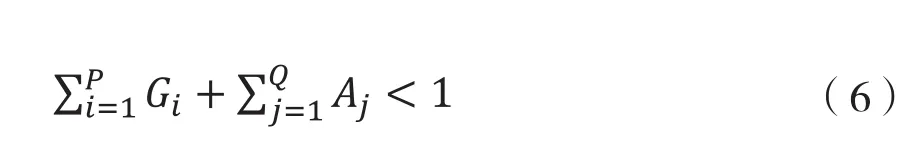
结合图1上证指数日收益率的分布情况和图2日收益率波动情况可以看出：上证综指的日收益率分布呈现尖峰厚尾特性，其走势没有显著的非平稳特征，序列围绕在零值附近波动，大部分时期波动范围在-0.06至0.06之间；同时日收益率序列有着一段时期波动持续偏小，一段时期波动持续偏大的显著集群效应特征。若日收益率数据残差序列具有长期自相关性，则样本数据特性完全符合GARCH模型的基本假设。对日收益率样本数据进行平稳性、自相性检验，其结果如图3和图4所示。

三、 实证分析

GARCH模型分为均值方程和方差方程两个部分，均值方程如下[13]：

以上证综指2014年1月2日至2015年6月30日日收益率作为样本数据，结合MATLAB软件对上证综指波动性进行实证分析与预测。

首先，对样本数据的基本统计特征进行分析，利用MATLAB绘制上证综指日收益率的直方图和日收益率走势折线图，执行结果如图1和图2所示。

图1　 收益率数据直方图

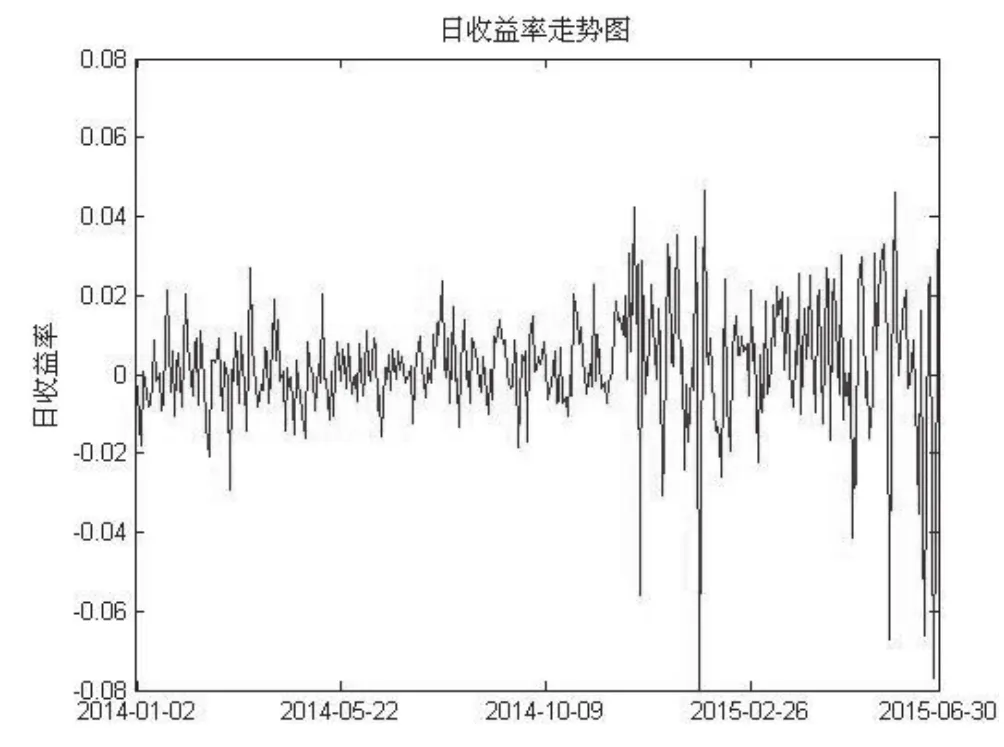
图2　 日收益率走势图

其中，k〉0，Gi〉0，Aj〉0；i=1,2,3…P；j=1,2,3…Q。

其中，JB检验获得执行结果：h=1，ADF检验hs=0，Engle拉格朗日乘数检验H1=1。

图3　 日收益率自相关图图

图4　 日收益率偏自相关图

分析执行结果可知：h=1，表示日收益率序列在默认显著性水平5%下拒绝其正态性假设；hs=0表示日收益率序列满足平稳性约束；H1=1表示样本数据存在ARCH效应。另外，从图3和图4可知，日收益率序列不存在显著的自相关特征，即日收益率满足ARMA（0,0）模型[14]。

图3还绘出了 Wald等（1991，1993）使用委员会报告中的远震数据反演断层滑动的结果。滑动的地震反演与大地测量反演之间的一致性相当差。最近Song等（2005）提出这种差异也许可用可能高达5km／s的超剪切破裂速度来解释。

从图5和图6可知，残差序列存在自相关性。同时，为进一步把握样本自相关的特征，对残差样本数据进行Q统计量和Engle ARCH 检验。执行结果在最大滞后阶数为1，默认显著性水平5%的条件下，H1=1，即收益率残差存在ARCH效应，无ARCH效应模型不适用。因此，采用GARCH模型来拟合收益率序列，用残差平方序列偏自相关函数来确定ARCH的阶，并观察该模型能否消除残差相关性。

接下来，对收益率残差序列是否存在自相关性进行显著性检验，绘制残差序列的自相关和偏自相关图，如图5和图6所示。

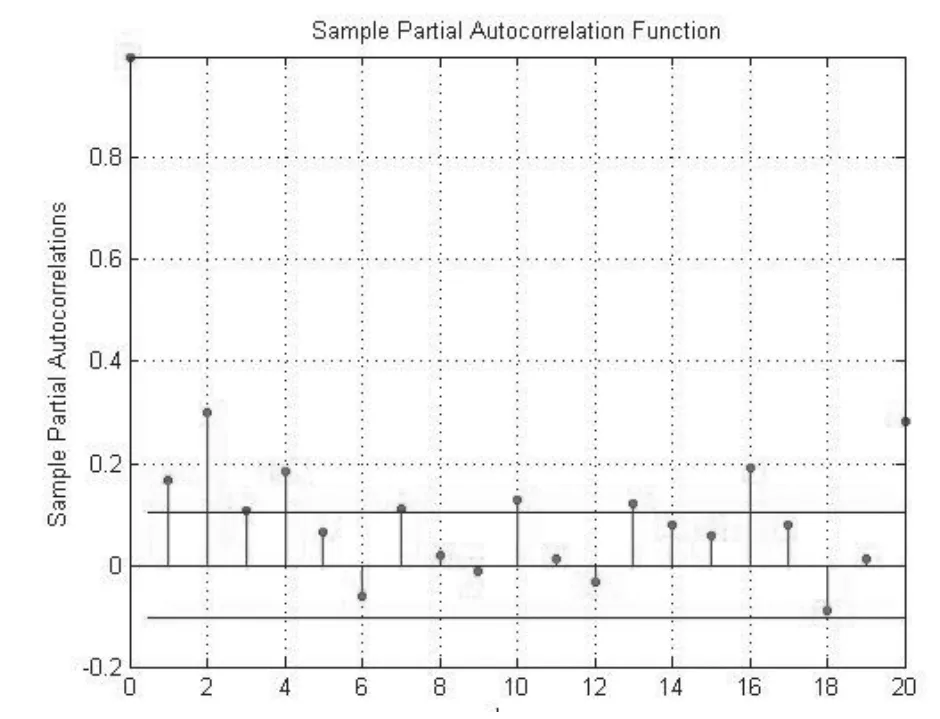
图5　 残差序列自相关图

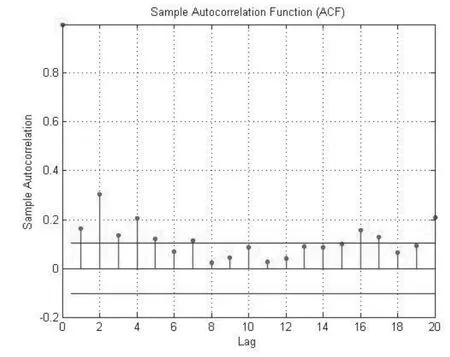
图6　 残差序列偏自相关图

式中，bi是得分向量，它包含着不同样本之间的信息关系，pi是加载向量，它包含着不同变量之间的信息关系，p是独立变量的个数，G是剩余矩阵。

Elasticsearch 是一个基于Apache Lucene 开发而来的实时的分布式搜索和数据分析引擎[4]。ES 能够快速、全面地浏览大规模数据集，适用于全文检索，结构化数据检索和数据分析；ES 强大的数据检索能力和优秀的二次开发能力，使得很多商业软件和平台如百度、GitHub、Wikipedia 等也采用ES 作为数据资源检索的核心组件。通过文献的系统综述[5-8]，我们总结ES 具有以下突出优点：

通过运用似然比检验统计量的方法，发现GARCH（1，1）模型适合样本数据的分析和预测。其执行结果如表1所示。

经研究发现,实验组脑卒中偏瘫患者的治疗效果和患者的生活质量明显好于对照组患者。根据统计学分析,差异具有统计学意义,P<0.05。详情见表1。

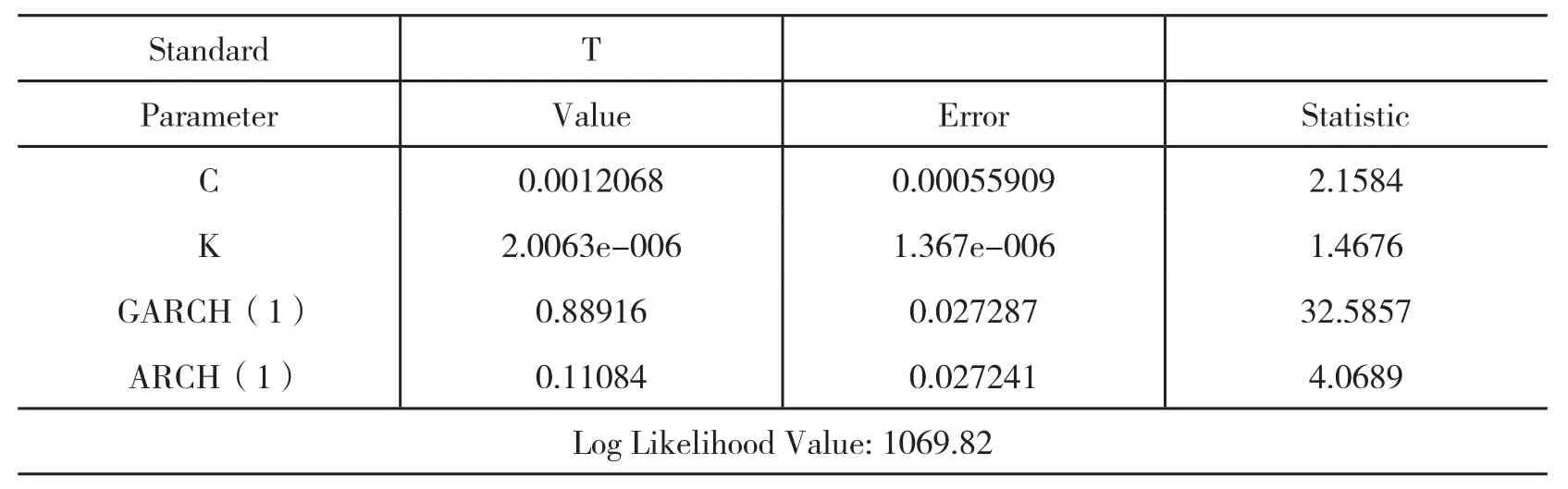
表1　GARCH模型执行结果表

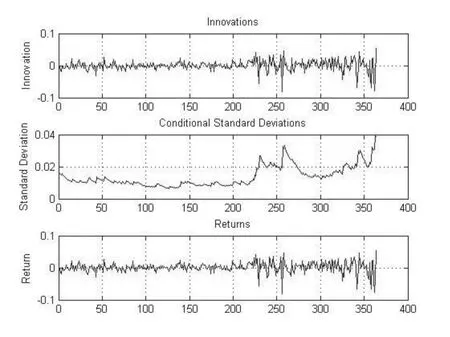
图7　 GARCH模型拟合图

根据表1和图7的输出结果可知，GARCH模型由均值方程和方差方程两个部分构成，形式如下。

对方程进行Q统计量检验，检验结果表明：在滞后阶数为1，默认显著性水平5%的条件下，收益率残差不存在ARCH效应。在GARCH模型的参数方程求出后，可以根据参数方程对收益率波动进行模拟预测，其10天和30天的波动率预测图如图8和9所示[15]。

图8　 10天波动率预测图

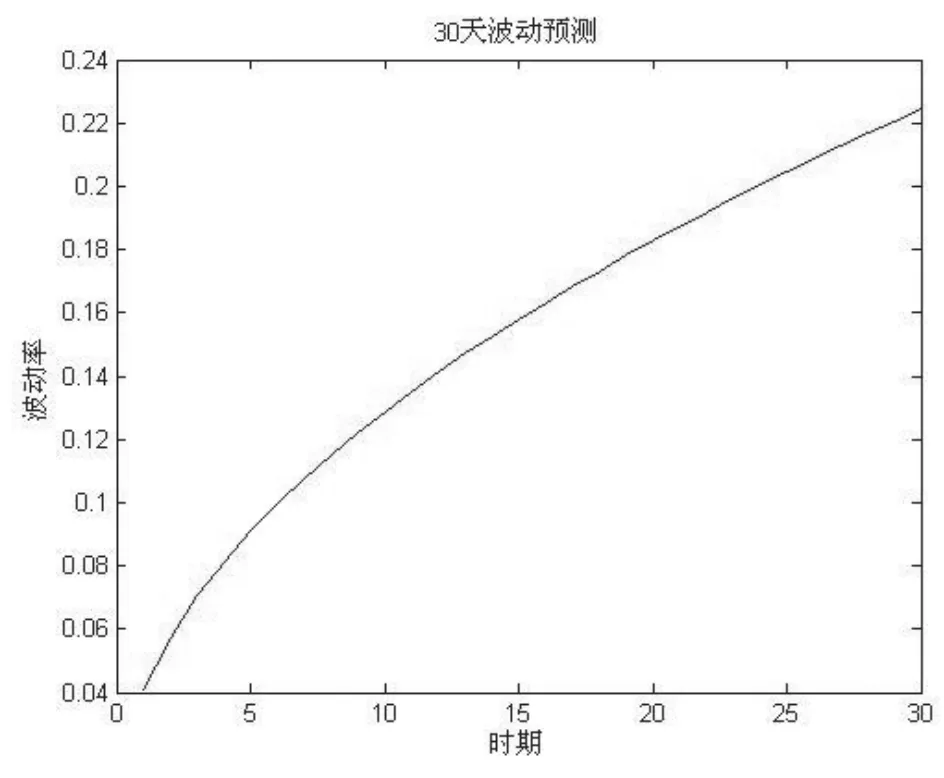
图9　 30天波动率预测图

四、 研究结论

综合以上拟合与预测结果可以得出以下几点结论：

（1）对比预测结果可以发现，随着时间间隔期的增长，上证综指的波动率有增大的趋势，但是增大速度是递减的。短期波动率在0.1-0.2左右，可以推断出股票市场短期趋于平稳，经济运行预期也逐渐趋向缓中求稳。短期内经济体和股票市场出现大的震荡概率不大，与实际结果一致。

（2）股票指数收益率呈现出尖峰厚尾分布，其残差序列异方差函数存在长期自相关性。这很好的符合了GARCH模型的模型假设。因此，GARCH模型在拟合和预测股票指数收益率波动方面展现出了极好的适用性和准确性[16]。

（3）投资者应该重视金融资产风险管理。除上证指数收益率外，其他金融资产收益率时间序列分布特征也与股票指数收益率具有相同的统计特性。因此，GARCH模型可以推广到金融资产风险管理中，可以在金融资产风险管理中起到导向性的作用。

参考文献：

[1]李文君,尹康. 多元GARCH模型研究述评 [J]. 数量经济技术经济研究,2009,(9).

[2]叶青. 基于GARCH和半参数法的VaR模型及其在中国股市风险分析中的应用 [J]. 统计研究, 2000,(12).

[3]Ding, Z Granger, C W J Engle, R F. A Long Memory Property of Stock Market Returns and a New Model [J]. Journal of Empirical Finance, 1993 ,1:83~106.

[4]Pagan, Adrian R. Two Stage and Related Estimators ad Their Applications, Review of Economics and Studies, 1986, 53: 517~538.

[5]Bollerslev. Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics,1986,31:307~ 327.

[6]龚锐,陈仲常. GARCH族模型计算中国股市在险价值风险的比较研究与评述[J].数量经济技术经济研究, 2005,(7).

[7]刘志东. 多元GARCH 模型结构特征、参数估计与假设检验研究综述 [J]. 数量经济技术经济研究,2010,(9).

[8]马超群,王宝兵. 基于Copula-GARCH 模型的外汇期货最优套期保值比率研究 [J]. 财经论坛,2011,(12).

[9]王辉, 谢幽篁. 中国商品期货动态套期保值研究:基于修正ADCC 和DADCC-GARCH 模型的分析 [J]. 世界经济,2011,(12).

[10]王天一,赵晓军,黄卓. 利用高频数据预测沪300指数波动率—基于Realized GARCH模型的实证研究 [J]世界经济文汇,2014,(5).

[11]魏红燕,孟纯军. 基于GARCH模型的短期汇率预测 [J].经济数学, 2014,(1).

[12]Lonathan, D Cryer, Kung—Sik Chan.Time SeriesAna1ysis with Applications,Second Edition [M].SPringer Science + Business Media, 2008.

[13]Ruey, S Tsay. An Introduction to Ana1ysis of Financia1 Data [M]. John Wiley ＆Sons, 2012.

[14]Laurent, S Peters, J P. GARCH:An Ox Package for Estimating and Forecas—ting Various ARCH Models [J]. Journal of Economic Surveys , 2002,16:447~485.

[15]郑志勇. 金融数量分析一基于MATLAB的编程 [M].北京航空航天大学出版社, 2009.

[16]吴育华,刘喜华.基于经济管理中数量化方法 [M].经济科学出版社, 2008.

责任编辑：胡燕京

Prediction and Analysis of SSEC's Yield Rate Fluctuation

LI Cong LIU Shi-qi ZHANG Wei-wei
( School of Economics, Qingdao University, Qingdao 266071, China )

Abstract:Investors are warned by the Chinese stock-market's recent huge shock that risk-management must be reviewed, if they want to keep a stable and healthy fi nancial market. The stock-market index's fl uctuation has close relationship with the economy. Therefore, this paper takes SSEC's yield rate as the study object, combining with its statistical characteristics. Great fi tting and forecasting results are obtained when analyzing and predicting the yield rate fl uctuation based on the GARCH model through MATLAB.

Key words:index yield rate; fl uctuation prediction; GARCH model

作者简介：李聪（1987-），男，山东济宁人，青岛大学博士生，研究方向为保险经济学、金融工程与风险管理；刘诗绮（1994-），女，山东青岛人，青岛大学经济学院，主要研究方向为金融计量、金融风险管理与保险等；张伟伟（1990-），男，山东烟台人，青岛大学经济学院研究生，主要研究方向：保险经济学。

收稿日期：2015-09-12

中图分类号：F830.91

文献标识码：A

文章编号：1005-7110（2015）06-0120-06