离散Kirchhoff型方程非平凡解的存在性

王庆云

(山西建筑职业技术学院基础部，太原 030006)

离散Kirchhoff型方程非平凡解的存在性

王庆云

(山西建筑职业技术学院基础部，太原 030006)

针对离散Kirchhoff型方程解的存在性问题，本文首先将其转化为矩阵形式，同时给出了相应的能量泛函，进而利用变分方法，将该问题的解转化为能量泛函的临界点.当非线性项满足超线性条件时，根据临界点理论中山路引理，证明了该问题至少存在一个非平凡解。

Kirchhoff型方程：变分方法：山路引理

1 引言及主要结果

本文主要利用山路引理研究离散Kirchhoff型方程：

(1)

非平解的存在性，其中N≥3是一个给定的整数，[1,N]表示离散区间{1,2,…,N}，a，b>0是常数，△表示由△u(k)=u(k+1)-u(k)所定义的向前差分算子，△2u(k)=△(△u(k)),且∀k∈[1,N],f(k,·)∈C(R,R)满足f(k,0)=0.显然问题：式(1)有平凡解u=0.因此，我们所感兴趣的是问题式(1)非平凡解的存在性。

对于问题式(1)，本文要求非线项f满足超线性条件:

(2)

(3)

记:

注式(1)下文中λi,i∈[1,N]表示下列线性特征问题：

本文所得结论为:

定理1 若条件式(2)，式(3)，(f1)及(f2) 成立，则问题(1)至少有一个非平凡解。

众所周知，Kirchhoff型方程:

(4)

是由Kirchhoff在文献[1]中研究可伸缩绳的自由振动的经典D′Alembert波动方程过程中提出的一种实际存在的方程。关于基尔霍夫型问题的经典研究，在文献[2-3]中作者已考虑了它的可伸缩绳横向振动的长度变化。然而，上述问题自Lions在文[4]中给出一个抽象框架之后引起了人们极大的关注，一些重要而非常意义的结果被得到，见文献[5-7]。最近，许多作者利用变分法在给出非线性项在零点和无穷远点的可解性条件的情形下来研究Kirchhoff型方程解的存在性问题，并取得一定的成果[8-14]，问题式(1)是问题式(4)的离散化形式，关于问题式(1)解的存在性结论甚少，仅在2013年，文献 [15]利用临界群和Morse理论讨论过问题式(1)解的多重性。本文与文献[15]的假设条件不同，因而所得结论丰富了离散Kirchhoff型方程的研究结果。

2 能量泛函及基本引理

u=(u(1),u(2)…,u(N))T,f(u)=(f(1,u(1)),f(2,u(2)),…,f(N,u(N)))T,

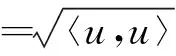
C1,p‖u‖p≤‖u‖≤C2,p‖u‖p

(5)

特殊地，有:

(6)

和:

(7)

容易知道问题式(1)的矩阵形式为：

(a+b‖u‖2)Au=f(u)

注意到f(k,·)∈C1(R,R),则J是一个具有一阶F-可微的泛函，并且:

J′(u)=(a+b‖u‖2)u-A-1f(u),u∈E

因此问题式(1)在E上的解等价于J∈C1(E,R)的临界点。

为了给出本文主要结论的证明，我们需要一些关于临界点理论的相关知识，现将本文所用到的主要内容叙述如下。

定义1[16]设E是一个Banach空间，J∶E→R是C1泛函。如果对任意{zn}⊂E，条件:

{J(zn)}有界，J′(zn)→0(n→∞)

蕴含{zn}有收敛子列，则称泛函J在E上满足(PS)条件。

令：

3 主要结果的证明

下面给出定理1的证明。首先证明J满足(PS)条件。

设{un}⊂E,β>0使得：

(8)

我们仅需要证明{un}是有界的。假设结论不成立，若:‖un‖→∞，n→∞.

由条件(f1)可得，∃M1>0使得：

所以当‖un‖→∞时，J(un)→+∞，矛盾。因此J满足(PS)条件。

下面证明J满足山路引理的几何条件。由条件式(2)式知，∃δ>0使:

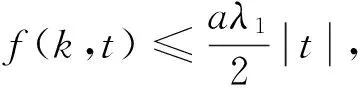
从而：

结合条件(f2)可得∃C3>0使:

因此:

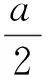
再由式(5)与式(6)有：

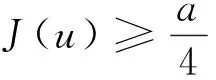
由p>3即知∃r>0充分小，使：

(9)

显然：

J(θ)=0

(10)

另一方面，取v0∈RN，使‖v0‖=1,m>0，且v0(k)>0.由式(3)可知，∃M2>0使得：

进一步，结合式(6)及式(7)，∃M3>0使得:

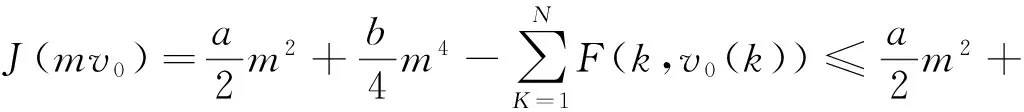
故：

J(mv0)→-∞，m→∞

于是，RN中存在元素u0=m0v0满足:

(11)

根据式(9)，式(10)及式(11)，即知山路引理的条件满足，故J必有临界值c*≥cr>0，即存在u*∈RN，使J(u*)=c*，且J′(u*)=0，由于J(θ)=0，故u*≠θ.证毕。

[1]KIRCHHOFFG.Mechanik[M].TeubnerLeipzig，1883.

[2]BERNSTEINS.Suruneclassed′oguationsfonetionnellesauxdorivoespartielles[J].BullAcaxiSciURSSSdr，1940(4)：17-26.

[3]POHOZAEVSI.Acertainclassofquasilinearhyperbolicequations[J].MatSb，1975(96)：152-166.

[4]LIONSJL.Onsomequestionsinboundaryvalueproblemsofmathemati-calphysics[C]∥ContemporaryDevelopmentsinContinuummechanicsandPartialDifferentialEquations，North-HollandMath.Stud.North-Holland，Amsterdam，1978：284-346.

[5]AROSIOA，PANIZZIS.Onthewell-posednessoftheKirchhoffstring[J].TransAmerMathSoc，1996(348)：305-330.

[6]CAVALCANTIMM，DOMINGOSCAVALCANTIVN，SORIANOJA.GlobalexistenceanduniformdecayratesfortheKirchhoff-Carrierequationwithnonlineardissipation[J].AdvDifferentialEqu，2001(6)：701-730.

[7]ANCONAPD，SPAGNOLOS.GlobalsolvabilityforthedegenerateKirchhoffequationwithrealanalyticdata[J].InventMath，1992，108：247-262.

[8]PERERAK，ZHANGZT.NontrivialsolutionsofKirchhofftypeproblemsviatheYangindex[J].JDifferentialEqu，2006，221：246-255.

[9]SUNJJ，TANGCL.ResonanceproblemsforKirchhofftypeequations[J].DiscreteandContinousDynamicalSys，2013(5)：2139-2154.

[10]ZHANGZT，PERERAK.Sign-changingsolutionsofKirchhofftypeproblemsviainvariantsetsofdescentflow[J].JMathAnalApp1，2006，317：456-463.

[11]LIYH，LIFY，SHIJP.ExistenceofapositivesolutiontoKirchhofftypeproblemswithoutcompactnessconditions[J].JDifferentialEqu，2012，253：2285-2294.

[12]XUJX，ZHANGFB.MultiplicityandconcentrationofpositivesolutionsforaKirchhofftypeproblemwithcriticalgrowth[J].JDifferentialEqu，2012，253：2314-2351.

[13]YANGY，ZHANGJH.Nontrivialsolutionsofaclassofnonlocalproblemsvialocallinkingtheory[J].JApplMathLett，2010，

23：377-380.

[14] CHENG B T，WU X.Existence results of positive solutions of Kirchhoff Problems[J].Nonlinear Anal，2009，71：4883-4892.

[15] YANG J P，LIU J S.Nontrivial solutions for discrete Kirchhoff type problems with resonance via critical groups[J].Advances in Difference Equ，2013，308：1-14.

[16] CHANG K C.Infinite Dimensional Morse Theory and Multiple Solutions Problems[M].Birkhauser Boston：MA，1993.

Existence of Nontrivial Solutions for a Discrete Kirchhoff Type Equation

WANG Qing-yun

(Foundation Courses Department of Shanxi Architectural College，Taiyuan 030006，China)

The existence of nontrivial solutions to a discrete Kirchhoff type problem was studied.The matrix form and the corresponding energy func-tional of the above problem were given in this paper，then the desired solutions were equivalent to the critical points of the energy functional by variational methods.When the nonlinear term met the superlinear growth conditions，it was proved that the problem had at least one nontrivial solution via Mountain Pass Lemma of critical point theory.

kirchhoff type problems，variational methods，mountain pass lemma

1673-2057(2015)01-0072-04

2014-10-13

山西省自然科学基金(201311004-3)

王庆云(1959-)，女，教授，主要研究方向为泛函分析。

O177

A

10.3969/j.issn.1673-2057.2015.01.015