基于晶体塑性理论的面心立方单晶变形研究

安红萍，丁艳红，李 婷

(太原科技大学材料科学与工程学院，太原 030024)

基于晶体塑性理论的面心立方单晶变形研究

安红萍，丁艳红，李 婷

(太原科技大学材料科学与工程学院，太原 030024)

借助晶体塑性理论，通过ABAQUS/UMAT用户子程序的二次开发，实现了基于位错运动的塑性本构描述。通过晶体塑性有限元模拟，研究了单向拉伸过程中，晶体旋转及晶粒取向对变形结果的影响，获得了晶体旋转角度与应变的对应关系，晶粒初始取向对滑移启动及变形程度的影响规律；模拟结果与Schmid定律一致，验证开发的晶体塑性模型的正确性。

面心立方单晶；塑性变形；数值模拟

晶体材料的弹塑性变形是一个复杂的过程，与很多因素相关，包括变形温度，应变速率，变形量，加载方式等宏观因素，以及晶粒大小，晶体取向，位错滑移，孪生等微观因素[1]。晶体塑性理论能够深入揭示晶体材料的变形规律。20世纪20年代，由Schmid，Taylor，Mises等人建立了单晶体塑性理论和多晶体塑性理论[2]。随着理论基础的逐步完善和计算机能力的提高，晶体塑性理论与有限元法结合形成了晶体塑性有限元法[3]。晶体塑性有限元法作为一种将材料的塑性变形机理与宏观力学响应有效结合在一起的研究手段，成为材料科学领域一个广泛应用的模拟工具[4]。

1 晶体塑形理论及有限元模型

1.1 晶体运动学

在晶体塑性运动学理论中，晶体变形是由晶体的位错沿特定的滑移系滑移和晶格畸变造成的，总的变形梯度F可以分解为：

F=F*·Fp

(1)

其中，F*为弹性变形梯度，由弹性变形和刚性转动产生，Fp为塑性变形梯度，由晶体在滑移面上沿着滑移方向均匀剪切形成[5]。

由于塑性变形是由滑移系引起、由滑移系上的平均剪切滑移率确定的，因此塑性变形梯度可表示为：

(2)

其中，γα为第α滑移系的滑移剪切率，mα为第α滑移系的滑移方向，nα为第α滑移系的滑移面法向。

1.2 晶体塑性本构关系

晶体弹性性质不受滑移变形影响，因此单晶弹性本构关系可表示为：

(3)

其中，L为晶体弹性模量四阶张量，D*为弹性部分应变张量。

晶体本构方程为：

(4)

1.3 动力学方程

对于率相关的塑性变形，硬化方程中剪切应变率与分切应力使用幂指数关系描述的，表示为：

(5)

对于面心立方晶体，单晶滑移系的硬化演化方程为：

(6)

hαβ=qαβhβ

(7)

(8)

其中，hαβ为滑移系硬化模量矩阵，qαβ为潜硬化矩阵，h0为初始硬化率，gβ为第β滑移系的当前硬化模量，gS为流动饱和应力值，α为经验常数[6]。

2 单晶拉伸的有限元分析

通过用户子程序UMAT[7]将上文中晶体塑性模型离散化后集成到ABAQUS软件中，实现基于晶体塑性理论的材料本构关系描述。

2.1 建立单晶模型

通过ABAQUS/CAE建立单晶体拉伸变形模型，具体步骤如下：

(1)建立几何模型：在ABAQUS/CAE中建立尺寸为10×10×10mm3的几何模型；而后采用5×5×5的网格划分，模拟单元采用C3D8型，方便施加材料属性和边界条件，创建网格部件。

(2)施加边界条件：在模型顶部上端面设定参考点RP-1，且与上端面设置分布耦合约束。设置参考点RP-1，位移边界条件：U2=3mm，UR1=UR3=0，下端面位移边界条件：U2=UR1=UR3=0，如图1所示。

图1 FCC单晶体塑性变形有限元模型Fig.1 Finite element model of FCC single crystalplastic deformation

(3)设定材料模型及参数：根据典型FCC(面心立方晶体)材料模型[3]，设置晶体塑性有限元模拟计算中用到的材料参数如表1所示。

表1 FCC晶体模型中的材料参数Tab.1 Material parameters of FCC crystal model

h0/MPahααhαβτS/MPaτ0/MPa541.511109.560.8

2.2 模拟结果分析

2.2.1 晶体旋转

图2是晶体取向{100}<010>，拉伸方向为[010]，拉伸变形量30%，应变速率0.1 s-1条件下，滑移系开动导致FCC单晶体外形变化的结果，可以看出，FCC单晶体在受到单向拉伸之后，变形均匀，但是单晶体在拉伸过程中沿着拉伸方向发生塑性变形的同时，因变形协调的需要还伴随着围绕拉伸方向的晶体转动。图3是晶体变形过程中晶体旋转角度与应变的关系，由图所示，随着应变的不断增大，晶体围绕拉伸轴的旋转角度增大。

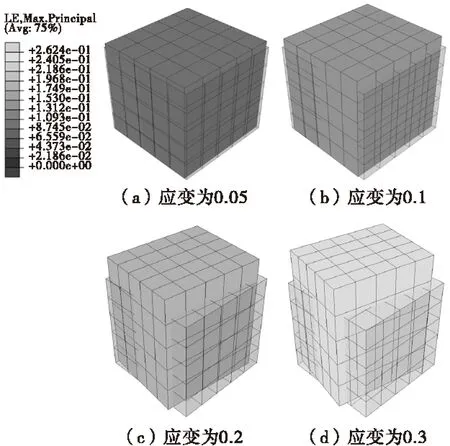
图2 FCC单晶体滑移系开动导致的晶体变形Fig.2 FCC single crystal deformation caused byactivated slip system

图3 晶体旋转角度与应变关系Fig.3 The relationship between strain and rotation angleof single crystal

上述现象与图4所示的单晶体拉伸试验过程一致，如图4(b)所示，在外力作用下，晶体的一部分相对于另一部分沿一定的晶向和晶面作相对移动，即通过滑移机制产生塑性变形。此时，由于夹头的约束作用(类似于上述有限元模型的底部约束)，试样的轴和端面的空间位置不能随意改变，故在拉伸过程中发生滑移的同时会产生图4(c)所示的晶面弯曲以协调滑移变形的继续发生。其原因如图5所示，当拉应力作用在中间某一晶块时，该拉应力可以分解为垂直于滑移面的正应力和位于滑移面内的最大分切应力，前者分别作用于上下两层，构成一对力偶，以实现并维持晶面的弯曲；对于后者，若其与滑移方向不一致时，又可分解为平行和垂直于滑移方向的两个力，平行于滑移方向的分力将会构成一对作用在滑移块上下的力偶，促使晶块发生旋转，以实现滑移方向与最大切应力方向的重合，实现晶体的转动，获得图2所示的效果。因此，将模拟结果与试验现象对比可以看出，该模型能够反映出单晶体拉伸过程中晶面转动的细观现象。

图4 单晶体拉伸变形过程Fig.4 Single crystal tensile deforming

2.2.2 应力应变分析

对拉伸方向为[010]，拉伸变形量30%，应变速率0.1 s-1，取向为{110}<001>的单晶模型进行模拟，将模拟结果在ABAQUS/VISUALIZATION中进行后处理得到其开动滑移系的变形情况。

图5 切应力的分解Fig.5 Resolving of shear stress

图6 单晶体不同应变下Mises应力分布云图Fig.6 Mises stress distribution in the single crystal at different strain rate

图7 模拟应力应变曲线Fig.7 Simulated stress-strain curve

图6为不同应变下应力分布云图，分别对应图7的各个点，由图可知变形过程中单晶模型Mises应力分布均匀。由图可以看出，Mises应力达到226 MPa时，开始塑性变形，出现屈服现象，随着塑性变形的进行，金属被逐渐强化，继续变形所需力不断提高，至最大应力值约400 MPa时，达到材料对最大均匀塑性变形的抗力。图7可以看出在硬化阶段曲线斜率逐渐减小，表明硬化速率逐渐降低，这是由于前文所述晶粒取向伴随晶体旋转导致滑移系的滑移方向逐渐趋于软取向的结果。超过400 MPa后，应力开始缓慢下降，发生软化。

图8给出了拉伸过程中，FCC晶体内典型滑移系的变化趋势。根据分析结果，将晶体内的12个滑移系按照其产生的剪切应变的大小分为三类，第一类：No.1、No.6、No.7、No.10；第二类：No.2、No.3、No.4、No.5、No.8、No.9；第三类：No.11、No.12.图8为典型滑移系剪切应变曲线图，以No.1、No.3、No.12三个滑移系为例，提取出其剪切应变曲线数据，绘制图形。可以看出，No.1滑移系数值恒为0，表明滑移系并未发生启动，拉伸方向与滑移系呈硬取向。滑移系No.3最大值仅为4.14E-36，几乎为0，表明No.3滑移系也没有启动。No.12滑移系随着应变量的增大，剪切应变不断增大，说明滑移系明显开动，拉伸方向与滑移系呈软取向，在晶体塑性变形中起到主要作用。

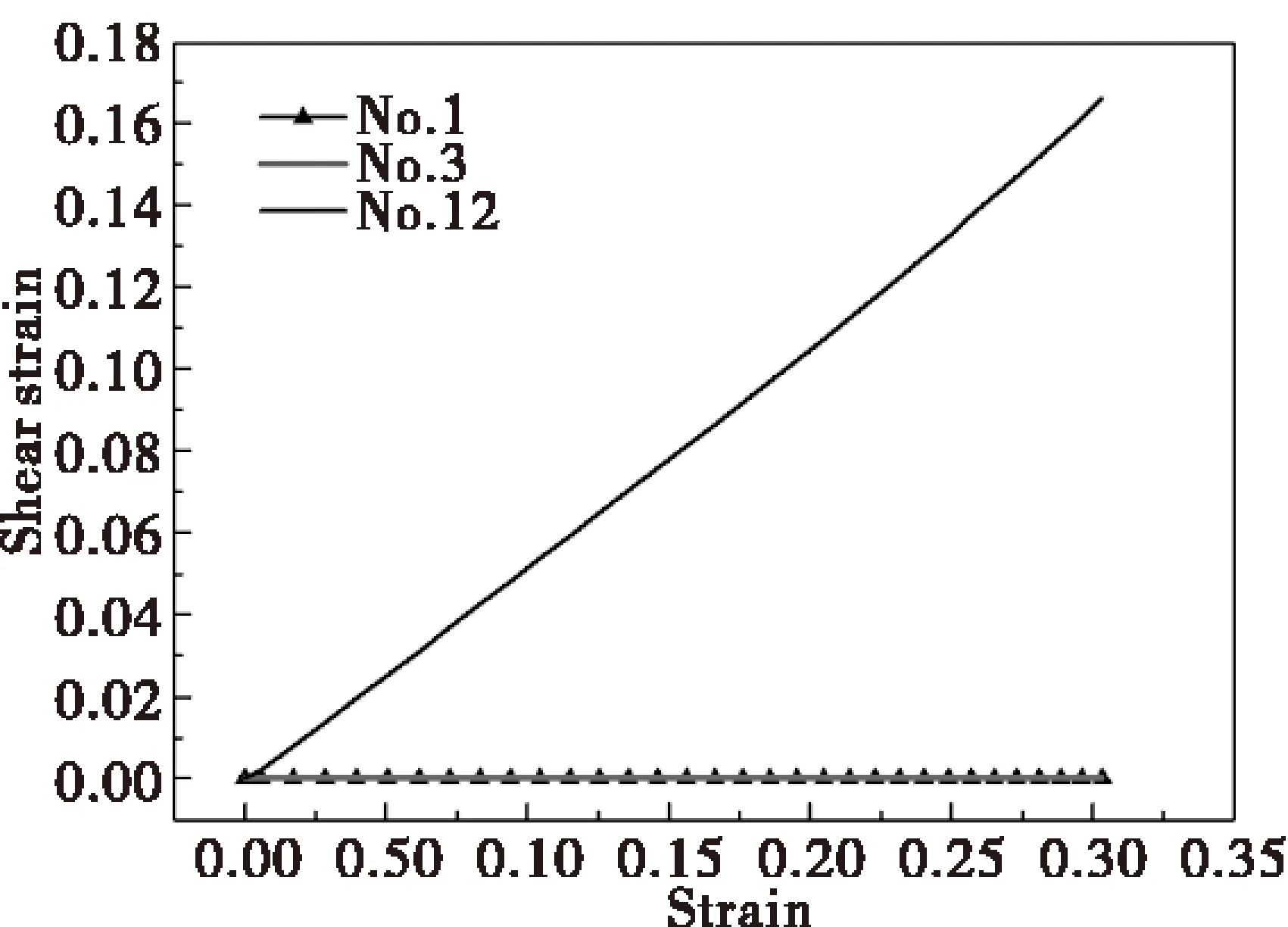
图8 典型滑移系剪切应变曲线图Fig.8 Shear strain of typical slip system

2.2.3 晶体初始取向与力学响应

分别赋予模型材料再结晶以及轧制过程中常易形成的织构取向，如表2所示，并设定拉伸方向为[010]，拉伸变形量30%，应变速率0.1 s-1的条件进行模拟。

表2 单晶拉伸模型的不同晶体取向Tab.2 Different crystal orientation of single crystal stretching model

图9 初始取向不同的拉伸应力-应变曲线
Fig.9 Stress-strain curves with different original crystal orientation

五种取向的单晶体拉伸应力-应变曲线如图9所示。可以看出，初始取向不同的晶体在单向拉伸过程中表现出的宏观响应明显不同：其中，取向最软的欧拉角为(0°，0°，0°)，屈服应力仅为213 MPa；取向最硬的欧拉角为(35°，45°，0°)，屈服应力达到338 MPa.另外，晶体取向为(60°，32°，65°)，在塑性变形过程中达到塑性屈服后，应力一直增大，呈现明显的硬化现象，并未发生其他四个取向状态下，略有软化的情况。

图10为应变达到0.3时，五种不同取向的单晶体内Mises应力分布情况。对于(60°，32°，65°)取向的单晶体内的Mises应力分布表现出明显的非均匀性，数值范围较大在347 MPa至1 121 MPa，其余四组初始取向的晶体Mises应力分布均匀。对于屈服应力较低的(0°，0°，0°)，Mises应力在数值上明显低于其他取向晶体，仅有396.4 MPa.对于屈服应力较高的(35°，45°，0°)，Mises应力在数值上明显高于其他取向晶体，达到596.1 MPa.上述现象表明，单晶体的宏观力学行为与其晶体取向及相对加载方向关系密切。

图10 应变为0.3，应变速率为0.1 s-1时不同初始取向单晶体Mises应力分布情况Fig.10 Mises stress distribution in the single crystal with different original orientation，strain and strain rate as 0.3 and 0.1 s-1

2.2.4 不同初始取向晶体滑移系的开动

按照Schmid定律(τ=σcosλcosφ=τc)，单晶体塑性变形开始时τc一定，但晶体位向不同会造成取向因子μ不同， 故单晶体的屈服极限σs是不确定的，因此会造成晶体力学响应的不同。图11表示了应变0.3时各个滑移系剪切应变的大小及分布情况。由图可以看出，不同初始取向的单晶体在拉伸状态下，滑移系的开动情况有很大差别。对于最软取向(0°，0°，0°)，启动的滑移系数量最多共有8个，且剪切应变数值相同为0.079；对于无软化效应的取向(60°，32°，65°)，开动的滑移系最少，只有4个，且剪切应变分布明显不均，剪切应变最大的9号滑移系数值达到了0.626远大于其余开动的滑移系，而2号滑移系剪切应变最小，只有0.006.除了取向(60°，32°，65°)之外，其余取向所启动的各个滑移系统剪切应变值大小相当，分布均匀，与图10 Mises应力分布情况相符。

图11 应变0.3时不同取向的单晶体内各个滑移系剪切应变大小及分布情况Fig.11 Shear stain distribution of different slip system in the single crystal with different original orientations under strain as 0.3

3 结论

采用的本构模型能够较好的模拟面心立方单晶单向拉伸变形过程中的晶体转动、晶粒取向对宏观力学响应的影响，模拟数据体现了晶粒初始取向与滑移系启动顺序之间的定量关系，并验证了Schmid定律。由此可见，本文所建立的晶体塑性有限元模型可以正确的描述面心立方单晶基于滑移理论的变形情况。

[1] 万建松.基于有限变形晶体滑移理论的单晶力学行为及应用研究[D].西安：西北工业大学，2003.

[2] SCHMID E.Plasticity of Crystal [M].New York：Oxford University Press，1935.

[3] 何东.双相多晶钛合金微观塑性变形机理与组织演化的定量研究[D].哈尔滨：哈尔滨工业大学，2012.

[4] 黄晓华.纯钛塑性变形行为的晶体塑性有限元模拟[D].哈尔滨：哈尔滨工业大学，2010.

[5] CHOI S H.Simulation of stored energy and orientation gradients in cold-rolled interstitial free steels[J].Acta Materialia，2003，51(6)：1775-1788.

[6] 张强.钛晶体塑性变形机制的分子动力学研究[D].哈尔滨：哈尔滨工业大学，2010.

[7] 李青.浅谈ABAQUS用户子程序[C]∥ABAQUS用户年会论文集.北京：清华大学出版社，2002.

Research on Plastic Deformation of Face-centered Cubic Single Crystal Based on Crystal Plasticity Theory

AN Hong-ping，DING Yan-hong，LI Ting

(Taiyuan University of Science and Technology，School of Materials Science and Engineering，Taiyuan 030024，China)

With the help of crystal plastic theory，a plactic constitutive description based on dislocation motion was obtained by means of the secondary development of ABAQUS/UMAT user subroutine.A crystal plactic finite element model was built，and the effect of crystal rotation and crystal orientation on deformation was studied during a face-centered cubic single crystal during uniaxial tension.The corresponding relationship between crystal rotation and strain，the influence law of the initial crystal orientation on slip system activation and macroscopic mechanical response，were obtained.The simulated result had better agreement with the Schmid's law，which verified the correctness of the crystal plastic model.

face-centered cubic single crystal，plastic deformation，numerical simulation

1673-2057(2015)01-0034-06

2014-09-18

山西省科技攻关项目(20130321010-04)；太原科技大学博士科研启动项目(20122057)

安红萍(1973-)，博士，副教授，主要研究方向为塑性成形理论及模拟技术。

TG316

A

10.3969/j.issn.1673-2057.2015.01.007