一种基于相似系数的权重确定方法

晋民杰，王 快，范 英，陈敏娜，王雯雯

(太原科技大学，太原 030024)

一种基于相似系数的权重确定方法

晋民杰，王 快，范 英，陈敏娜，王雯雯

(太原科技大学，太原 030024)

分析常用的主观权重确定方法，提出一种基于相似系数的权重确定方法，给出其数学解释、建模过程和计算步骤，指出在实际评价、决策中可以利用描述指标向量相似程度的“相似系数法”来求出相似系数，进而确定相似权，即为指标权重。最后，结合叉车维修决策中的实例验证其可行性，并与利用层次分析法确定权重在计算过程复杂性和计算结果准确性方面进行比较，证明其计算的准确性和简易性。

权重确定；相似系数；相似权；层次分析法

评价指标的权重确定问题是多指标综合评价过程中的核心问题。文献[1]提出可以根据专家的名望、地位、所属专业、对决策问题的熟悉程度等来让专家确定指标的权重，或利用每个专家对决策群体中的所有专家进行评估确定指标权重，在文献[2]中称其为主观赋权法。文献[3]提出，在专家判断信息的整合过程中，根据专家意见确定指标权重至关重要，在确定指标权重时，主观赋权法是通过决策者之间相互比较评价来确定权重的，其已被广泛应用于综合评价过程的权重确定问题中，常用的主观赋权法有AHP法、Delphi法、环比评分法等。

主观赋权法要求对专家或专家之间有较高的熟知程度，评估的主观性和不确定性很大[1]。然而在实际决策过程中主观赋权法的诸多要求是很难达到的，况且指标权重的实际值并不一定与专家主观赋权一致，因为专家每次所做的判断不一定严格与自己实际的决策准则一致，即便严格一致，其决策判断准则也在随实际经验累积和对评价对象的熟知程度而不断调整的。当同一位专家，面对不同的问题决策时，其可信度同样也不可能是完全一样的。

针对专家主观确定指标权重的不足，本文提出一种基于相似系数的指标权重确定方法，该方法可以有效消除在判断权重方面人为因素二次干扰，不再让专家再次主观参与指标权重判断，而是通过相似规律归纳专家的判断意向，找出更加客观的反映专家意见的信息，从而更精确地确定指标权重。

1 理论来源

1.1 数学依据

1.2 数学解释

专家决策问题没有最优解，主要研究问题在于选择出群决策方案中与理想方案最接近的决策方案，这样群决策方案中与理想方案的接近程度便可以反映出方案的优劣[5]；同理，专家根据个人经验给出的决策意见的集中程度则反映出了指标的权重，群决策中对于某指标的评价越集中则说明该指标的权重越大，对于某指标的评价越离散则说明该指标的权重越小。不同专家评价集之间的接近程度反映在数学上，就是向量的接近程度，而相似系数可以刻画向量的接近程度。

在实际问题求解过程中，是无法知道理想的指标权重的，可取样本评价值的算术平均作为理想的指标权重，因为它在“平均”的意义下反映了对象的总体评价情况。这样，便可根据对某单一指标的评价向量与总体评价向量的“接近”程度来确定指标权重，此想法便是利用相似系数这一数学原理确定指标权重的关键。根据相似系数的数学求解过程给出求解指标权重的具体数学过程为：首先确立单指标评价矩阵，然后假设各评价指标拥有相同的权重求得综合评价矩阵，再通过相似系数法求得各指标的相似系数和相似权，所得的相似权重即为各评价指标的实际权重。

2 数学建模

2.1 相关定义

评价对象集合X={x1,x2，…,xn},xi∈X,i=1,2,…,n；

评价指标集合I={I1,I2,…,Im},Ij∈I，j=1，2，…,m；

令Xij为对第i个评价对象第j个评价指标的评价值，则每个评价对象xi有xi={x11,x12,…,x1m}；对每个评价值Xij有e个评价等级a1,a2,…,ae，令U表示评价等级空间，则U={a1,a2，…,ae}；令μijk=μ(xij∈ak)，k=1,2,…e,μ(xij∈ak)为xij∈ak的程度，则μ满足：

(1)

μ即为未确知测度，显然从式μ(xij∈U)=1知其在评价等级空间U上满足“归一性”，从式(1)看出其在评价等级空间上满足“可加性”[7]。

(2)

为xi的单指标测度评价矩阵，式(2)的行向量为xij的单指标评价向量[8]。

令ωj为第j个评价指标相对于其它指标的重要程度，则:

(3)

令μik=μ(xi∈ak)，即第i个评价对象属于第k个评价等级ak的程度，则:

(4)

由式(4)定义的μik称为未确知测度，称矩阵:

(5)

为多指标综合测度评价矩阵，称矩阵(5)的第i个行向量:

(μi1,μi2,…,μie)

(6)

为xi的综合测度评价向量[8]。

2.2 基于相似系数的权重确定

评价向量“相近”程度用相似系数法，相似权即为评价指标的权重。至此，我们便可以给出基于相似系数的权重推导方法：

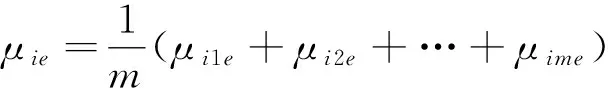
(7)

单指标评价向量与综合测度评价向量相近程度的相似系数为:

(8)

(9)

ωj即为相似权，相似权便可作为评价指标的权重。相似权是建立在单指标评价向量与综合指标评价向量相近程度的基础上确立的，指标的单指标评价向量与综合指标评价向量越“相近”，其权重就越大。能够更加客观的反映评价指标的客观权重。可归纳利用相似系数求指标权重的步骤：

算出式(2)和式(4)，利用式(2)和式(4)进而算出式⑤；

利用算出的式(2)和式(5)按式(8)算出相似系数rj，进而利用式(9)算出相似权，即为指标权重。

3 结果验证

层次分析法是最为常用的主观赋权法，其通常被应用于综合评价中的指标权重确定，结果的正确性也得到了实例验证。为简单说明利用相似系数确立权重的优越性，以叉车维修决策中的作业操作件的综合评判为例进行说明，并与利用层次分析法确立指标权重进行比较。

在叉车作业操作件的维修评判中依据叉车安全评价的相关标准主要考虑3个三级指标：E11操作手柄应完好，无损坏，操作方便舒适；E12作业手柄释放时，操作件应能回至中位，停止作业动作，手柄操纵力≤120N；E13操作件图示符号标识应完整清晰。

3.1 相似系数法

以项目实际进行中13位专家的打分为准，便可建立对3台叉车相应指标测度评价矩阵，分别为：

假定3个评价指标具有相同的权重，令ωj=1/3(j=1,2,3)

由此推出综合测度评价矩阵：

按式⑧得：(r1,r2,r3)=(559/1521,887/1521,

340/1521)

进而按式⑨求得相似权：(ω1,ω2,ω3)=(0.313,0.496,0.191)，即为3个指标的相应权重。

3.2 层次分析法

(1)构造判断矩阵，根据1-9标度法(如表1所示)设计因素两两比较判断表格(如表2所示)供13位专家打分使用，两表格分别如：

表1 1-9标度法参照表Tab.1 Reference table of 1-9 scale method

(2)计算经特征值和特征向量。

表2 三级指标重要性两两比较表Tab.2 Pairwise comparison table of importance of the three indicators

(3)一致性检验。

经计算得出最终结果，如表3所示。

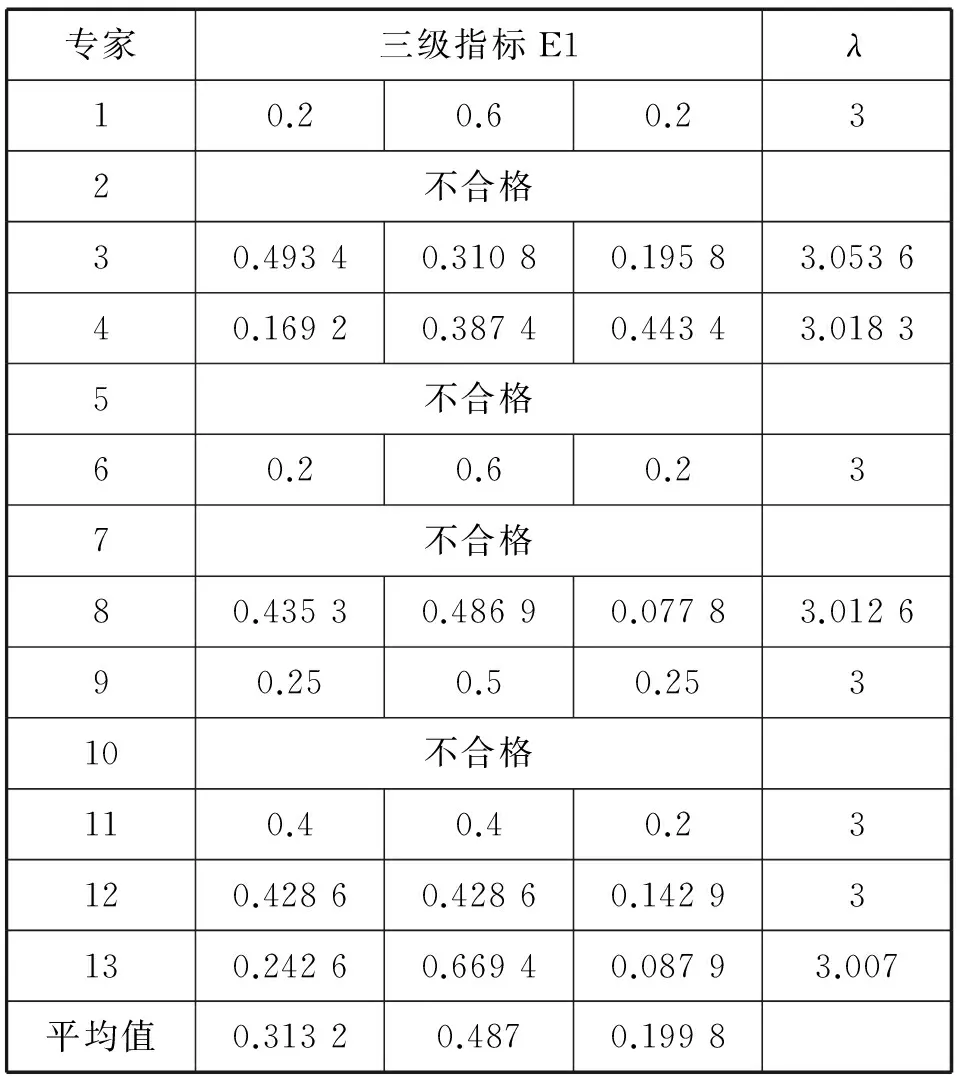
表3 层次分析法权重结果Tab.3 Weight results-AHP

得出的特征向量平均值即为3个指标的权重，即(ω1,ω2,ω3)=(0.313 2,0.487,0.199 8).

3.3 两种方法的比较

比较两种方法的计算结果，差异很小，显然基于相似系数的权重方法在权重结果确定的准确性上完全符合要求。比较计算过程可知，层次分析法需单独制定表格让专家参照标度法对指标两两比较打分并进行计算来确定权重，增加了专家主观性、计算量和复杂性，但是基于相似数的权重确定方法省去了专家对评价指标两两比较打分的过程，既可以减少专家主观权重的干扰又可以减少工作量，它直接借鉴综合评判或策略选择时专家对各评价指标的打分结果，从中提取出“隐藏”的更加客观的权重信息确定权重，简化了工作量，增加了计算结果的准确性、客观性。

4 结论

针对同一个决策问题，整个专家决策群的群决策意见反映出了决策的客观性，个别的决策判断结果是不影响整体决策判断趋向的。简言之，相对于整体决策中的异常判断，我们更相信群体决策。基于以上想法本文提出了一种基于相似系数的权重确定方法，给出了数学解释、数学建模过程、计算步骤，结合实例验证了计算过程并将计算结果与层次分析法计算的结果进行比较，验证了本方法计算的准确性和客观性。利用相似系数法确定权重时，必须有一个较为庞大的决策群，这也是本文找13位专家进行决策的原因，只有提供足够充分的信息，才能找到“隐藏”其中的权重信息，找出的指标权重才能更加准确、客观。所以，在策略选择或综合评判中使用相似系数法确定指标权重具有一定的借鉴意义。

[1] 李琳，刘雅奇，李双刚.一种群决策专家客观权重确定的改进方法[J].运筹与管理，2011，2(4)：77-81.

[2] 宋光兴，邹平.多属性群决策中决策者权重的确定方法[J].系统工程，2001，15(1)：19-22.

[3] VARGAS L G.An overview of the analytic hierarchy process and its application[J].European Journal of Operational Research，1990，48(1)：2-8.

[4] YANG WEI-RONG，Jaccard系数[EB/OL].http：//baike.baidu.com/view/9579150.htm?fr=aladdin，[2014-06-27].

[5] 张慧颖，张妍.另一种新的多指标综合评判方法[J].数学的实践与认识，2010，40(7)：20-24.

[6] 张宇，刘雨东，计钊.向量相似度测度方法[J].声学技术，2009，28(4)：532-536.

[7] 张跃，王时标，陈树勋，等.未确知测度和信比测度[J].哈尔滨建筑工程学院学报，1991，24(2)：1-8.

[8] 陈娟，刘凌.基于熵权的未确知测度模型在湖库富营养化评价中的应用[J].河海大学学报(自然科学版)，2008，36(4)：452-455.

A Method of Weight-determining Method Based on Similarity Coefficients

JIN Min-jie，WANG Kuai，FAN Ying，CHEN Min-na，WANG Wen-wen

(School of Transportation and Logistics，Taiyuan University of Science and Technology，Taiyuan 030024，China)

This study summarized the common subjective weight determination method.A new weight-determining method based on similar coefficients was put forward，and its mathematical explanations，modeling process，and computing steps were presented，which proved that，in practical evaluation and determination， similar coefficients method describing index vector similarity was effective to get similar coefficients，and therefore to determine similar weight，i.e.，index weight.Finally，the case of forklift maintenance decision confirmed the feasibility of similar coefficients method and demonstrated that it was more accurate in computing results and simplifying computing process than the Analytic Hierarchy Process in weight determination.

weight determination，similarity coefficients，similarity weight，AHP

1673-2057(2015)01-0060-05

2014-09-17

“十二五”国家科技支撑计划(2011BAK06B05)

晋民杰(1964-)，男，教授，主要研究方向为载运工具运用工程等；通讯作者：王快，E-mail：sdtawkk@163.com

U279

A

10.3969/j.issn.1673-2057.2015.01.012