摩擦因素对结合面法向接触状态的影响
2015-04-07杨松华张学良温淑花陈永会兰国生
杨松华,张学良,温淑花,杨 波,陈永会,兰国生
(太原科技大学机械工程学院,太原 030024)
摩擦因素对结合面法向接触状态的影响
杨松华,张学良,温淑花,杨 波,陈永会,兰国生
(太原科技大学机械工程学院,太原 030024)
基于综合考虑微凸体完全弹性、弹塑性和完全塑性的三维接触分形理论,并引入微接触点域扩展因子,进而考虑摩擦的影响,建立了修正的结合面法向接触模型。该模型的仿真研究结果表明,摩擦的影响使得临界弹塑性接触面积增大,从而使变形机制中弹塑性变形和塑性变形的比例增大;在相同的真实接触面积下,考虑摩擦因素影响所对应的接触载荷比不考虑摩擦因素影响所对应的接触载荷较小,且随真实接触面积的增大两种情况下所对应的接触载荷之间的差距将逐渐变大。同时还分析了不同参数条件对法向接触状态的影响。
结合面;三维分形模型;修正因子;摩擦因素;法向接触
在机械工作过程中,机械零部件结合面之间将产生振动位移和噪声,加剧结合面间的摩擦和磨损,由于摩擦与磨损对接触表面的影响,使结合面之间表现出非常复杂的动力学特性,影响机械的加工精度和增加不必要的能耗。因此对结合面间引入摩擦因素的研究至关重要,在这方面,根据经典的G-W接触模型,Chang[1]等人以及后来Kogut和Etsion等人[2-3],通过考虑粘着力的影响以及弹性和弹-塑性接触点承受切向载荷的能力,得到了计算金属材料结合面间的静摩擦因数模型;朱育权[4]等在MB分形模型的基础上,建立了考虑弹塑性变形以及结合面间摩擦的作用的分形模型;李小彭[5-6]等人在二维分型理论基础上推出了考虑摩擦因素影响的结合面法向与切向接触阻尼分形预估模型,并对此进行了实验、仿真与模拟。
在接触界面间,由于摩擦副之间相互运动而使相对运动表面上发生摩擦磨损,不同材料的摩擦磨损特性的差别必然会反映在相互运动的摩擦副表面形貌上,本论文针对这种现象,基于三维接触分形理论以及上述学者的研究,在原分形模型中引入微接触点域扩展因子,并把摩擦因素引入到三维接触分形理论中,建立了修正的综合考虑完全弹性、弹塑性和完全塑性的粗糙表面三维接触分形模型,进而仿真研究了摩擦系数对粗糙表面接触状态的影响,并与不考虑摩擦因素影响的模型进行了对比分析。
1 各向同性粗糙表面形貌描述函数
可以用来描述各向同性粗糙表面形貌的W-M函数为[7]:
(1)
式中,D为粗糙表面轮廓分形维数,2
经典Hertz接触理论指出球形微凸体在压力Pa作用下发生弹性变形的变形量为[8]:
(2)
式中pa为作用于接触界面间微凸体上的平均压力。E*为与两接触表面弹性模量有关的等效弹性模量,R是接触界面间微凸体的曲率半径。
当微凸体的变形处于完全弹性变形阶段时,其弹性接触面积ae为:
ae=a′/2
(3)
其中,a′为微凸体的截面积。
当两接触表面有相对滑动摩擦时,则微凸体开始屈服的临界平均压力pc为[4-9]:
P=1.1kμσs
(4)
式中,σs是屈服极限;μ为摩擦系数,kμ是与μ有关的摩擦力修正因子。
(5)
由式(4)与式(2)可得出接触界面间微凸体开始屈服时的临界弹性变形为:
(6)
由三维接触分形理论可知[7]:
(7)
(8)
从式(7)、式(8)以及式(6)可得接触面间微凸体开始屈服时的临界接触截面积为:
(9)
(10)

2 临界弹塑性接触状态
为了更准确地研究微凸体的弹塑性变形,文献[10]将弹塑性区域细分为两个区域:弹-塑性变形Ⅰ区域(δc≤δ≤6δc)和弹-塑性变形Ⅱ区域(6δc≤δ≤110δc),相应地,微凸体弹-塑性变形阶段接触面积和变形量之间的关系为[10-11]:
当δc≤δ≤6δc时,
(11)
当6δc≤δ≤110δc时,
(12)

(13)
(14)
3 微凸体塑性接触面积
当微凸体的变形量δp>110δc时,微凸体发生塑性变形,则其接触面积为:
ap=2πRδ=a′
(15)
4 接触界面间的真实接触面积与载荷
4.1 真实接触面积
从三维接触分形理论可知粗糙表面的微凸体截面积分布函数[12-13]:
(16)

(17)
可得结合面间理想真实接触面积为:
(18)
Ar=Are+Arp+Arep2+Arep1
(19)
式中:
(20)
(21)

(22)

(23)
4.2 接触载荷
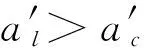
(24)
a′1.85-0.425D
(25)
a′1.526-0.263D
(26)
Fp=Hap
(27)
则结合面总接触载荷为:
(28)
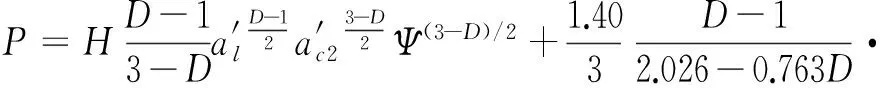
(29)
当D=2.5时:
(30)
根据微凸体截面积a′与实际接触面积a之间关系a′=2a带入式(29)、式(30)并将其进行无量纲化得:
当2 (31) 当D=2.5时: (32) 从文献[14-15]可知,一般工程的塑性指数范围为0.7-2.5,K通常取2.8,2 (1)图1为摩擦系数对微凸体临界弹性接触面积的影响,其中G*=1.0×10-8,φ=2.5,D=2.6.由图1可看出,由于摩擦力的作用使微凸体临界弹性接触面积ac增大,当摩擦系数较小时(μ<0.3)对αc的影响较小,但是当摩擦系数较大时即当μ>0.3时,临界接触面积急剧增大,从而使得实际接触面积中的完全塑性和弹塑性变形的接触面积比例增大。 (2)图2中Ar*=0.1,图2(a)可知,接触载荷随着分形维数的增大出现先减小后增大的非线性关系。在相同维数下,考虑摩擦因素的影响与不考虑摩擦因素影响相比,D<2.3时,考虑摩擦因素所需要的载荷比较大,而随着D的增大,当D>2.4以后两者载荷之间的差距逐渐减小。图2(b)可看出接触载荷随着塑性指数的增大而减小,且减小速率越来越小,且同一塑性指数下考虑摩擦因素影响的接触载荷要大于不考虑摩擦因素影响的接触载荷;图2(c)可得接触载荷随着分形特征长度参数的增大而增大,且同一分形特征长度参数下,考虑摩擦因素影响比不考虑摩擦因素影响所需的载荷比较大;图2(d)可得接触载荷随着摩擦系数的增大而增大。 (3)图3中G*=1.0×10-9,φ=2.5从4幅图可直观得出,在一定条件下,接触载荷随着真实接触面积的增大而增大,且在相同的真实接触面积下,考虑摩擦因素影响所对应接触载荷比不考虑摩擦因素影响所对应的载荷要小,且随真实接触面积的增大两种情况下所对应的接触载荷之间的差距将逐渐变大。 基于结合面三维接触分形理论,考虑结合面摩擦因数及结合面弹塑性接触变形,并引入微接触点域扩展因子,建立了修正的结合面三维接触分形模型。通过仿真计算分析,研究了结合面摩擦因素、塑性指数、分形参数对结合面接触状态的影响,结果表明:在一定条件下,由于受到摩擦因素的影响,微凸体切向变形受到摩擦力的牵制,从而使新建立的模型的接触载荷随着分形维数的增大先减小后增大,随着摩擦系数的增大而增大,随着塑性指数的增大而减小,随着真实接触面积的增大而增大,随着分形特征长度参数的增大程非线性增大;由于摩擦因素的影响使得临界弹塑性接触面积的增大,从而增大了整个变形机制中塑性变形与弹塑性变形所占的比例;在相同的塑性指数、分形特征长度参数下,考虑摩擦因素影响所对应接触载荷比不考虑摩擦因素影响所对应的载荷要大;而对于同一真实接触面积下,考虑摩擦因素影响所对应接触载荷比不考虑摩擦因素影响所对应的载荷要小,且随真实接触面积的增大两种情况下所对应的接触载荷之间的差距将逐渐变大。 图2 不同条件对接触载荷的影响 图3 考虑与不考虑摩擦因素Ar*与P*的关系Fig.3 The relationship between P* and Ar* with and without consideration of friction factor [1] CHANG W R,ETSION I,BOGY D B.Static Friction Coefficient model for metallic rough surfaces[J].J Tribol ASME,1988,110(1):57-63. [2] GREENWOOD J A,WILLIAMSON J B P.Contact of nominally flat surfaces[J].Proceedings of The Royal Society of London,1966,295(1442),300-319. [3] KOGUT L,ETSION I.A semi-analytical solution for the sliding inception of a spherical contact[J].ASME Journal of Tribology,2003,125(3):499 -506. [4] 朱育权,马保吉,姜凌彦.粗糙表面接触的弹性、弹塑性、塑性分形模型[J].西安工业学院学报,2001,21(2):150-158. [5] 李小彭,王 伟,赵米鹊,等.考虑摩擦因素影响的结合面切向接触阻尼分形预估模型及其仿真[J].机械工程学报,2012,23(12):46-50. [6] 李小彭,郭浩,刘井年,等.考虑摩擦的结合面法向刚度分形模型及仿真[J].振动、测试与诊断,2013,33(2):113-117. [7] YAN W,KOMVOPOULOS K.Contact analysis of elastic-plastic fractal surfaces[J].J Appl Phys,1998(84):3617-3624. [8] MAJUMDER A,TIEN C L.Fractal characterization and simulation of rough surfaces[J].Wear,1990(136):313-327. [9] JOHNSON KL.Contact mechanics[M].Cambri dge:Cambridge Univ Press,1985. [10] ZHAO Y W,MAIETTA D M,CHANG L.An asperity micro-contact model incorporating the transition from elastic deformation to fully plastic flow[J].ASME Journal of Tribology,2000,122(1):86-93. [11] 牛作证,张学良.结合面切向接触刚度三维分形模型[J].太原科技大学学报,2013,34(5):361-367. [12] WANG S,KOMVOPOULOS K.A fractal theory of the interfacial temperature distribution in the slow sliding regime:Part I Elastic contact and heat transfer analysis[J].Journal of Tribology,1994,116(4):812-822. [13] JI CUICUI,ZHU HUA,JIANG WEI.Fractal Prediction Model of Thermal contact conductance of Rough surfaces[J].Chinese Journal of Mechanical Engineering,2012,26(1):128-136. [14] YOU J M,CHEN T N.Statistical model for normal and tangential contact parameters of rough surface[J].Mech Engrs,2010,225:171-185. [15] 刘正伦.具可变形貌参数之微接触模型理论研究[D].台湾:国立成功大学,2006. Influence of Friction Factor on Normal Contact State of Joint Surface YANG Song-hua,ZHANG Xue-liang,WEN Shu-hua,YANG Bo,CHEN Yong-hui,LAN Guo-sheng (School of Mechanical Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,China) Based on the comprehensive consideration of asperity completely elastic,elastic-plastic and fully plastic three-dimensional contact fractal theory,the domain extension factor micro contact was introduced with consideration of the effect of friction,and a combination of modified surface method to contact model was established.The simulation results show that the influence of friction makes critical elastic-plastic contact area increase so that the deformation mechanism of plastic deformation and plastic deformation ratio increases.Under the same real contact area,considering the friction factors corresponding to the contact load is smaller than that without considering the friction factors of the load,and the increase of real contact area between the two cases of contact load gap will grow bigger.Moreover,the influences of different parameters on the normal contact state were analyzed. joint interfaces,three dimensional fractal model,correction factor,friction factor,the normal contact 1673-2057(2015)01-0054-06 2014-10-30 国家自然科学基金资助项目(51275328);山西省自然科学基金项目(2012011023-4) 杨松华(1987-),男,硕士研究生,主要研究方向为摩擦因素对机械结合面的影响。 TH113 A 10.3969/j.issn.1673-2057.2015.01.011



5 模型仿真
6 结论
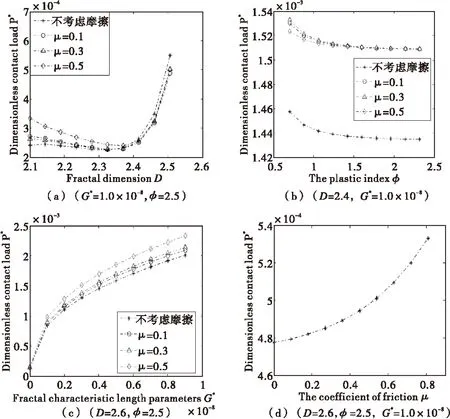
Fig.2 The influence of different conditions on contact load
