基于RSSI的改进四边测距机器人定位算法

谢 朦，陈志梅，邵雪卷

(太原科技大学电子信息工程学院，太原 030024)

基于RSSI的改进四边测距机器人定位算法

谢 朦，陈志梅，邵雪卷

(太原科技大学电子信息工程学院，太原 030024)

基于接收信号指示强度的测距特性和三边测距定位原理，提出了应用于机器人定位的改进四边测距定位算法，引入加权质心定位算法的思想，通过距离因子控制各个锚节点对定位精度的影响，并将锚节点之间的距离和信号强度作为修正RSSI的参考值。仿真结果表明，该算法不仅可靠性高，有效避免了信息淹没现象，而且在不增加通信成本的基础上提高了机器人的定位精度。

RSSI；无线传感器网络；三边测距定位；四边测距定位；机器人定位

随着计算机技术、微电子技术和无线通信等的发展，机器人已经广泛应用于军事和民用领域，而机器人定位问题是实现机器人自主导航的关键。机器人定位[1]分为相对定位和绝对定位，绝对定位指机器人在不指定初始位置的情况下确定自己的位置，相对定位指机器人在给定初始位置的条件下确定自己的位置，是机器人定位处理中主要的研究方向。无线传感器网络(Wireless Sensor Networks，WSN)因具有大规模、自组织、动态性、可靠性的特点而应用于机器人定位中，是国内外研究的热点之一。

现有的机器人定位算法通常通过测量节点的距离或角度信息，使用三边测量、三角测量或最大似然估计的方法计算节点位置来实现定位。常用的基于测距的定位算法有：RSSI (received signal strength indicator)[2]，TOA (time of arrival)[3]，TDOA (time difference on arrival)[4]和AOA (angle of arrival)等。典型的基于非测距的定位算法有：DV-hop(distance vector-hop)，APIT(approximate point-in-triangulation test)，凸规划算法(convex optimization algorithm)等。基于非测距的算法常常需要较多的观测站或者参考点才能获得较高的定位精度[5]，所以基于测距的定位算法应用较广泛。

文献[6]在三边测距定位算法基础上直接引入加权补偿，以抑制RSSI测量值的随机波动对定位的影响。该算法计算量小，实现简单，一定程度下改善了由环境影响导致的RSSI测量值不稳定问题，但对定位精度的改善不明显。文献[7]在三边定位算法的基础上建立了参考节点呈等边三角形排列的定位系统，分别实现了在两种测距模式下单移动目标的定位跟踪。该算法定位误差呈规律性，由三边向质心逐渐减小的趋势，但定位精度受传感器测距精度的影响较大。

为了解决上述问题，且基于RSSI低成本，能耗小，在动态环境中变化有规律性的特点，本文提出一种改进的四边测距定位算法。该方法通过解决三边测距定位算法的不足，引入加权质心定位算法，有效地减小了由RSSI测距误差对机器人定位精度的影响。

1 算法模型

1.1 无线信号渐变模型

由于易受传播环境的影响，无线信号在传播过程中会有不同程度的损耗，这将大大的影响基于RSSI定位算法的精度，因此选择合适的传输模型非常重要。常用的无线信号传输模型有Okumura-Hata模型，COST231-Hata模型，COST231-WIM模型，Standard Macrocell模型和室内传播模型，针对室内封闭的机器人定位应用环境，无线信号传输模型采用对数-距离模型[8]，如下所示：

(1)

式中，d表示发射端与接收端的距离，p(d)表示距离发射机为d时接收端接收到的信号强度，即RSSI值；p(d0)表示机器人距离发射机为d0时接收端接收到的信号功率；d0为参考距离，通常取d0为1 m；n是路径损耗(Pass Loss)指数，通常是由实际测量得到，障碍物越多n值越大，从而接收到的平均能量下降的速度会随着距离的增加而变得越来越快，X是一个以dBm为单位，平均值为0的高斯随机变量，反映了当距离一定时接收到的能量的变化。

1.2 三边测距定位算法

以下介绍三边测距定法算法：如图1所示，已知锚节点为A(xA，yA)、B(xB，yB)、C(xC，yC)三点，待测机器人位置坐标为O(x，y).首先根据上文介绍的RSSI测距方法可获得锚节点与机器人的距离，分别表示为dA、dB、dC，并且几何关系如下：

(2)

(3)

(4)

由式(2)-式(4)可确定机器人的坐标。

图1 三边测距原理图Fig.1 Schematics of trilateral localization

但在实际情况中，无线信号容易受到无线信道的影响，在传输过程中会发生反射、绕射和散射，引起传播信号的衰减，从而通过RSSI值测距会产生误差，以致3个圆不会交于一点，使三边测距定位算法失效，如图2所示。

图2 三边测距定位实际情况Fig.2 Practical situation of trilateral localization

(5)

(6)

(7)

即为图2中直线l1、l2、l3的方程，求解便可得到交点O的坐标，即为机器人位置坐标。这种方法可以减少RSSI测距误差，而且测距误差越相关，定位精度越高。

为了进一步提高机器人的定位精度，引入四边测距定位，即在三边测距算法的基础上增加一个锚节点定位。

设增加锚节点为D(xD，yD)，根据对距离作平方差求得交点坐标的方法，可分别得出，通过A、B、C三点得到机器人的位置估计O1(x1，y1)，B、C、D三点得到O2(x2，y2)，A、C、D三点得到O3(x3，y3)，A、B、D三点得到O4(x4，y4)，对O1O2O3O4求质心得机器人的位置O(x，y)，即：

(8)

由于四边测距定位本质是质心定位，故存在以下问题：

已知锚节点接收到的RSSI值不一样，所得的距离信息不一样，当各锚节点接收的信息方差很大时，定位误差就变得很大。

在四边测距中，每次取3个锚节点确定时，当出现以下情况时，对由相交的圆确定的直线求交点会出现错误的结果：

①由锚节点A到机器人的测量距离dA确定的圆A与锚节点B确定的圆B无交点，但由锚节点C确定的圆C与圆A和圆B均有交点；

②圆A与圆B、C均有交点，但圆B与圆C无交点；

③圆A、圆B和圆C均不相交。

考虑到以上四边测距定位的问题，并且由于RSSI定位受环境干扰非常大，距离越近，定位精度越高，本文提出在四边测距定位的基础上引入加权质心定位算法，即在每次定位估计中引入一个权值ω，有效地防止了信息淹没现象[9]，且加权值取为锚节点到机器人距离的g次方的倒数，即ω=1/dg，g为距离因子。利用距离因子体现锚节点对目标估计位置的影响程度(锚节点与目标节点越远，对目标节点估计的比重越小)。根据文献[10]可知，距离因子对加权质心定位算法精度有着不可忽视的影响，并且当g取1.82时，平均定位误差最小，即加权质心定位算法中距离因子的最优解。

(9)

式中，(x1，y1)(x2，y2)(x3，y3)(x4，y4)分别为通过四边测距定位算法得到的四次目标估计O1，O2，O3，O4的坐标，dA，dB，dC，dD分别为锚节点A，B，C，D到机器人的测量距离。

在实际情况中，同一个RSSI值在同一随机分布中代表的不同锚节点之间距离是不同的。计算时如果仅考虑机器到锚节点的RSSI值而没加入其它修正方法，算法就存在一定的定位误差[11]。所以在改进的四边测距方法的基础上，把锚节点之间的距离和信号强度同时作为校正RSSI的参考值。

RSSI(m)表示机器人收到锚节点M信号的RSSI平均值，pm表示机器人收到锚节点M的信号强度平均值，转换关系如下：

(10)

RSSI(mn)表示锚节点M收到锚节点N信号RSSI平均值，pmn表示锚节点M接收到锚节点N的信号强度平均值，则有：

(11)

dMN表示锚节点M和N之间的距离。dm表示以锚节点对M和N为参考时，代入式(12)计算得到的机器人到锚节点M的距离，如式(13)：

(12)

(13)

从而有：

(14)

由上可知，机器人到锚节点M的距离dM可以表示为所有的dm对于所有N的可能值的平均值，如下：

(15)

n0为锚节点M的通信半径内锚节点个数，由上式可得到校正距离dM.

2 算法步骤

根据上文提出的改进的四边测距定位算法，具体实现步骤如下：

(1)首先锚节点周期性地向周围环境发送自身位置信息和身份信息。

(2)通过渐变模型将RSSI值转换成距离信息，并将测得的距离按从小到大排序，取前4 个锚节点对机器人进行定位，若出现直线两两不相交的情形，则用后面的节点替换前一个节点，直到满足定位要求[12]。

(3)取步骤(2)中的四个锚节点，任取三个进行组合定位，得到机器人的四个位置估计值。

(4)对步骤(3)中得到的四个估计值运用公式(9)，通过加权质心算法得到机器人的估计坐标。

(5)对以上得到的机器人坐标通过公式(10)-(15)进行校正，即得到机器人的坐标。

3 仿真与分析

本文基于MATLAB7.0平台进行仿真模拟，选取传感器区域为50m×50m，空间场地为100m×100m，锚节点和机器人的真实位置均由系统随机给定，锚节点对机器人探测10次，锚节点的个数取10个，距离因子g取1.82，并在RSSI数据中添加均值为0，方差为5的高斯白噪声，代替实际环境中的干扰。衰减系数n取2，通过无线信号渐变模型，按照本文的算法步骤来进行仿真定位。图3为基于RSSI的三边测距定位方法的仿真图，图4为四边测距定位方法的仿真图，图5为改进四边测距定位方法的仿真图。其中三角代表机器人的真实位置，圆圈代表锚节点的位置，正方形代表机器人的估计位置。

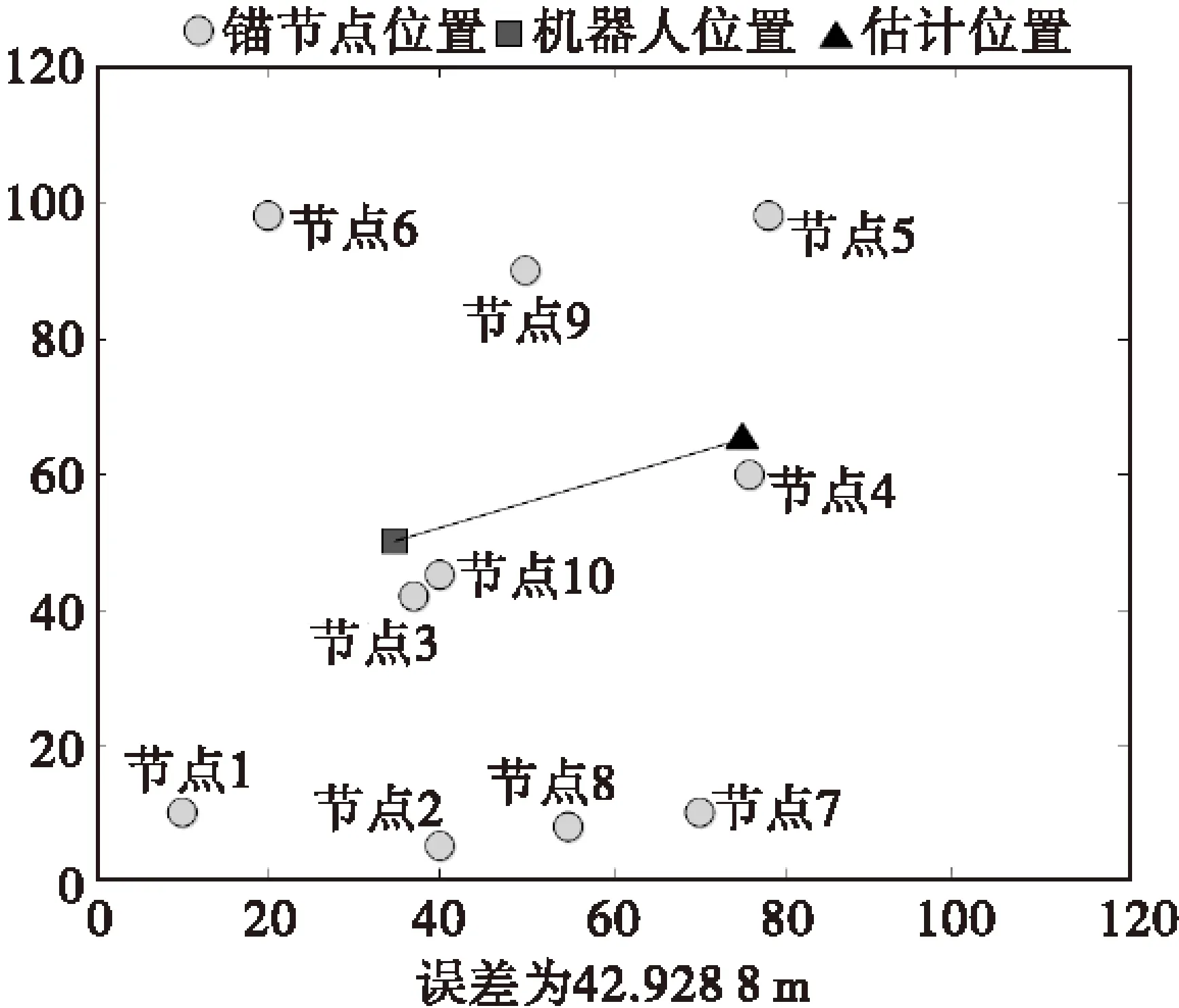
图3 三边测距定位仿真图Fig.3 Simulation of trilateral localization

图4 四边测距定位仿真图Fig.4 Simulation of quadrilateral localization

从图3～图5三组数据可以明显看出，在单次定位中改进后的四边测距定位算法，与传统三边定位算法和四边测距定法算法相比有着明显的优势。

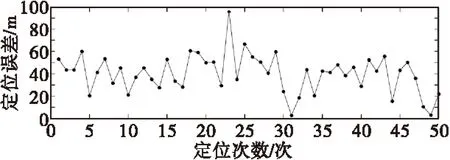
图6 三边测距定位算法误差仿真图Fig.6 Simulation of trilateral localization error

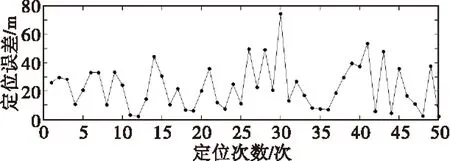
图7 四边测距定位算法误差仿真图Fig.7 Simulation of quadrilateral localization error

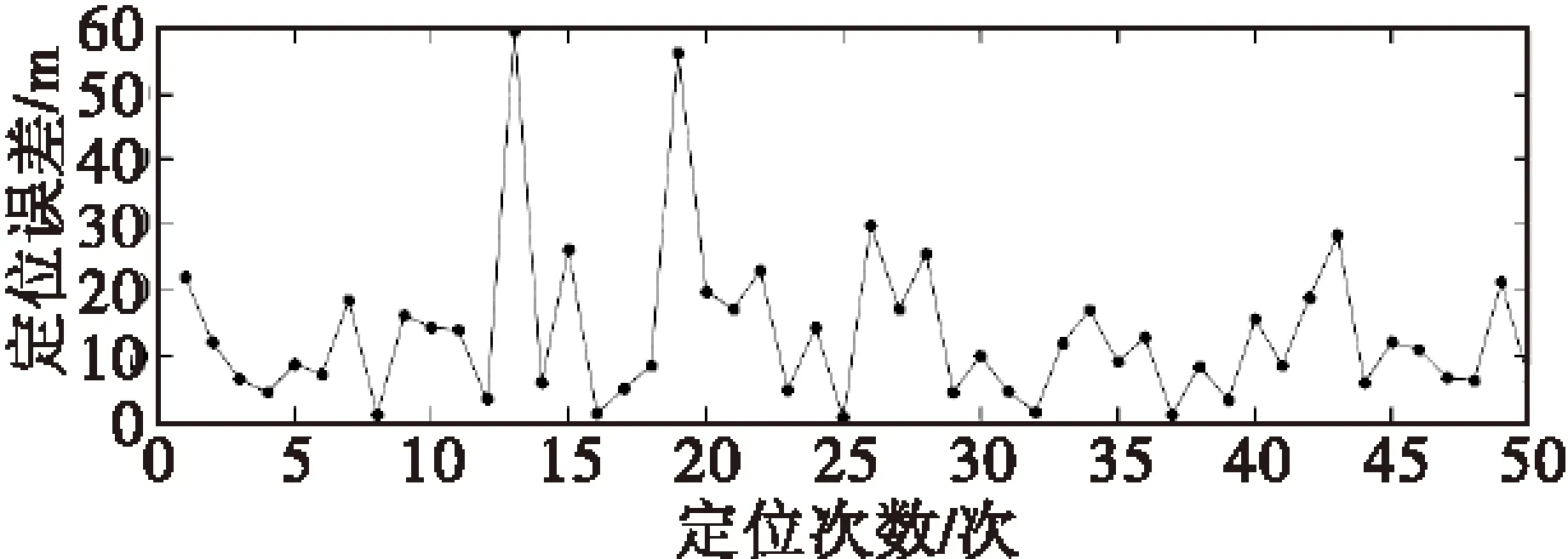
图8 改进四边测距定位算法误差仿真图Fig.8 Simulation of improved quadrilateral localization error

图6～图8分别为仿真50次三边测距定位方法、四边测距定位算法和改进的四边定位算法误差散点图。在锚节点均为10个且随意给定的情况下，由图对比易知，改进的四边测距定位算法误差小且变化范围小，因此改进的四边测距定位与传统三边测距算法、四边测距算法相比，精度高且可靠性高。

图9 锚节点数变化时三边测距定位算法误差仿真图Fig.9 Simulation of trilateral localization error with thechanging anchor nodes

图10 锚节点变化时四边测距定位算法误差仿真图Fig.10 Simulation of centroid localization error with thechanging anchor nodes

图9～图11分别为锚节点从5个增加到100个(每次增加5个)时，三边测距定位算法、四边测距定位算法和改进的四边测距定位算法的误差仿真图，由图可知，在相同的硬件通信条件下，改进的四边测距算法与三边测距定位算法、传统质心定位算法相比具有明显的优势。

图11 锚节点变化时改进四边测距定位算法误差仿真图Fig.11 Simulation of improved quadrilateral localizationerror with the changing anchor nodes

4 结论

本文提出的改进四边测距定位算法，完全采用几何运算，不需要循环迭代，具有很好的快速性，并且引入加权质心定位的思想，充分利用RSSI数据信息，通过距离因子控制各个锚节点对机器人定位精度的影响，避免了质心算法中的数据淹没现象和信息的丢失，并且将锚节点之间的距离和信号强度作为修正RSSI的参考值，在相同通信条件的基础上，进一步实现了机器人定位的高精度和高可靠性。

[1] 唐恒博，陈卫东，王景川，等.高精度高鲁棒性的轨道机器人全局定位方法[J].机器人，2013，35(5)：623-629.

[2] 陈昌祥，达维，周洁.基于RSSI的无线传感器网络距离修正定位算法 [J].通信技术，2011，44(2)：65-66.

[3] KIM S J，KIM B K.Accurate hybrid global self-localization algorithm for indoor mobile robots with two-dimensional isotropic ultrasonic receivers [J].IEEE Transactions on Instrumentation and Measurement，2011，60(10)：3391-3404.

[4] 史小红.基于TDOA的无线定位方法及其性能分析 [J].东南大学学报：自然科学版，2013，43(2)：252-257.

[5] 赵泰洋，郭成安.基于接收信号强度的非视距检测与修正算法 [J].数据采集与处理，2014，29(3)：397-402.

[6] 葛文涛，陈俊杰.基于三边定位的WSN锚节点加权补偿算法 [J].测控技术，2010，29(9)：92-95.

[7] 邵磊，赵京，张乃龙.基于超宽频距离传感器的移动目标定位系统 [J].传感器与微系统，2013，32(11)：63-74.

[8] PENG Y，LUO Q，LIU Z.An automatic evaluation system for IEEE1588 synchronization Clock Unit[C]∥Electronic Measurement & Instruments，2009.ICEMI′09.IEEE，2009：3-408，3-413.

[9] 陶志勇，路笋.基于ZigBee的修正加权质心定位算法研究与实现 [J].计算机应用与软件，2014，31(1)：123-126.

[10] 孙玮琢，迟卫，王擎宇.加权质心定位误差的反向修正法 [J].传感技术学报，2012，25(1)：114-118.

[11] 冯爱丽，乔钢柱，曾建潮.基于信标节点间距离的改进RSSI定位算法 [J].太原科技大学学报，2012，33(1)：6-9.

[12] 刘运杰，金明录，崔承毅.基于RSSI的无线传感器网络修正加权质心定位算法 [J].传感技术学报，2010，23(5)：717-721.

An Improved Quadrilateral Localization Algorithm of Robot Based on RSSI

XIE Meng，CHEN Zhi-mei，SHAO Xue-juan

(School of Electronic and Information Engineering，Taiyuan University of Science and Technology，Taiyuan 030024， China)

Based on the performance of received signal strength indicator (RSSI)and the principle of trilateration localization algorithm，an improved quadrilateral localization algorithm in robot localization is proposed.The improved algorithm，which introduced the idea of weighted centroid algorithm，affected the positioning accuracy through the control of each anchor node by the distance factor.What′s more， the distance between anchor nodes and signal intensity is taken as the reference of correcting RSSI.The simulation shows that not only the information drown can be effectively avoided，but also the positioning accuracy of robot localization can be improved without increasing the communication cost.

trilateral localization algorithm，improved quadrilateral localization algorithm，reference of correcting RSSI，robot localization

1673-2057(2015)01-0018-06

2014-09-23

山西省自然科学基金(2014011020-2，2014011020-1)

谢朦(1988-)，女，硕士生，主要研究方向为鲁棒控制、智能检测技术等；通讯作者：陈志梅，教授，E-mail：zhimeichen400@163.com

TP242

A

10.3969/j.issn.1673-2057.2015.01.004