知识与能力并重方法与思想兼顾
——以“圆”为例谈复习课的例题设计
2015-04-06江苏省泰州市苏陈中学韩新正
☉江苏省泰州市苏陈中学 韩新正
知识与能力并重方法与思想兼顾
——以“圆”为例谈复习课的例题设计
☉江苏省泰州市苏陈中学 韩新正
初三复习除了梳理概念、构建知识框架等,还离不开例题的选择和教学,选择什么样的例题是每个初三老师都必须面对的问题.本文以“圆”这一章为例,立足“知识与能力并重,方法与思想兼顾”的选题思路,谈谈复习课的例题选择和设计,供参考.
一、设计理念
1.教学内容分析
本文以苏科版《义务教育教科书·数学》为复习用书,本书关于“圆”这一章内容中的“垂径定理”和“切线长定理”标注了“※”号(不作为考试内容);删除了“弦心距”、“圆的两条平行弦所夹的弧相等”、“圆与圆的位置关系”等内容,这和《义务教育数学课程标准(2011年版)》的要求是一致的.本章的复习重点是点和圆的位置关系,圆的切线的性质和判定定理;难点是借助于例题教学,归纳解题方法,形成数学思想,培养学生“通性通法”的解题能力,养成“回到概念”的解题习惯.
2.例题编排意图
本章例题选择的策略是放慢节奏,小坡度起步,教学目标分阶段达成.对每道例题,力求从知识、方法、能力、数学思想多个方面进行挖掘,充分发挥例题的最大效益.例1尽量多地涵盖“圆”中涉及的基本概念和知识,目的是借助于例题梳理本章知识结构,同时关联其他知识,如直角三角形、勾股定理、锐角三角函数、特殊四边形的判定和性质、二次根式的化简等知识;例2突出“模型思想”教学,使学生会从生活背景中抽象出数学模型,初步感知解答圆的“通法”;例3侧重解题方法归纳,通过列方程、运用相似形、构造勾股定理等方法解题,归纳解题方法,提炼解题思想,培养学生“通法”解题习惯;例4综合运用所学知识,引导学生关注中考重点和热点,在传统题中注入时尚元素,培养学生“用数学思考”的习惯.比如,通过巧妙编排,融合平面直角坐标系、函数、点的运动等,培养学生综合解决问题的能力.
二、例题设计
例1如图1,已知:P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是圆上一点,连接PD,且圆的半径r=4,PC=PD=BC.下列结论:①PD与⊙O相切;②四边形PCBD是菱形;③PO=AB;④∠PDB=120°;⑤(的长为正确的序号是____________________.

图1
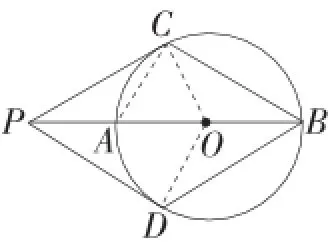
图2
解析:①如图2,连接CO,DO,由PC与⊙O相切,得∠PCO=90°,易证△PCO≌△PDO(SSS),得∠PCO=∠PDO=90°,所以D与⊙O相切.
②易证△CPB≌△DPB(SAS),由BC=BD,得PC= PD=BC=BD,所以四边形PCBD是菱形.
③连接AC,易证△PCO≌△BCA(ASA),得AC=CO,所以AC=CO=AO,得∠COA=60°,所以∠CPO=30°,PO= AB.
④根据四边形PCBD是菱形,∠CPO=30°,得DP=DB,所以∠DPB=∠DBP=30°,得∠PDB=120°.
⑤在Rt△PCO中,∠PCO=90°,∠CPO=30°,得∠POC=60°,所以∠DOC=120°,的长
说明:本例设计的目的,主要帮助学生系统整理本章基本知识,并进一步关联起和圆有密切联系的相关知识,帮助学生建构解决圆的问题的知识体系,同时,对本章题目的解题方法、思想方法进行渗透,两次通过“全等三角形的判定”解决问题,引导学生发现“全等三角形的判定”是解决这部分题目的“通法”,为解决综合题准备知识和方法.
例2如图3是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA、OB、OC抽象为线段,有OA=OB=OC,且∠AOB=120°,折线NG—GH—HE—EF表示楼梯,GH、EF是水平线,NG、HE是铅垂线,半径相等的小轮子⊙A、⊙B与楼梯两边相切,且AO∥GH.

图3
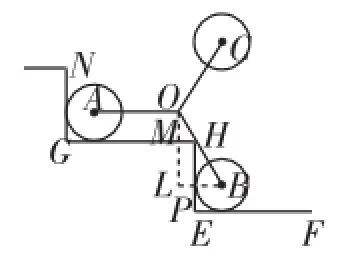
图4

图5
解析:(1)如图4,设P为⊙B与HE的切点,连接BP并延长,过点O作OL⊥BP于点L,交GH于点M,所以∠BPH=∠GHE=90°,所以BL∥GH.因为AO∥GH,所以BL∥ AO∥GH.因为∠AOB=120°,所以∠OBL=60°.又因为OL∥HE,所以∠BHP=30°.在Rt△BPH中
(2)如图5,作HD⊥OB,设P为⊙B与HE的切点,连接BP,PH的延长线交BD的延长线于点L,所以∠LDH=∠LPB=90°,所以△LDH∽△LPB,所以AO∥PB,∠AOD=120°,所以∠B=60°,所以∠BLP=30°,所以DL=■3DH,LH=2DH.因为因为0≤DH≤3,所以解得
说明:本例的设计基于两点考虑,一是对课标核心概念“模型思想”的建立,让学生经历三个小轮的手拉车在“爬”楼梯的情境,从中抽象出几何图形,并利用相似三角形、解直角三角形、特殊角的三角函数等知识求解模型的过程;二是培养学生解决问题的能力,设计具有实际背景的问题,本例的手拉车是现实生活中常见情景,从这一常见的背景中,引导学生思考并解决问题.
例3如图6,已知直线l与⊙O相离,OA⊥l于点A, OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.

图6

图7
解析:(1)略.
(2)延长AP交⊙O于点D,连接BD,设圆的半径为r,则由OA=5,OP=OB=r,在Rt△ABO中,AB2=OA2-OB2=52-AC,所以52-r2=-(5-r)2,解得r=3,所以AB=AC= 4.因为PD是直径,所以∠PBD=90°=∠PAC.因为∠DPB=∠CPA,所以△DPB∽△CPA,所以所以⊙O的半径是3,线段PB的长
(3)如图7,作线段AC的中垂线MN,过点O作OE⊥ MN,所为⊙O与直线MN相交,所⊙O与直线l相离,所以r<5,所
说明:本例设计侧重于基础知识和基本技能的训练,使学生养成“回到概念”解题的良好习惯.本例具有代表性、典型性,有着一类题目共性的解法,能通过例题的讲解,使学生获得解一类题目的方法,并形成稳定的思维模式.
(1)求证:直线FC是⊙A的切线;
(2)求点C的坐标及直线FC的解析式;
(3)有一个半径与⊙A的半径相等,且圆心在x轴上运动的⊙P.若⊙P与直线FC相交于M、N两点,是否存在这样的点P,使△PMN是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
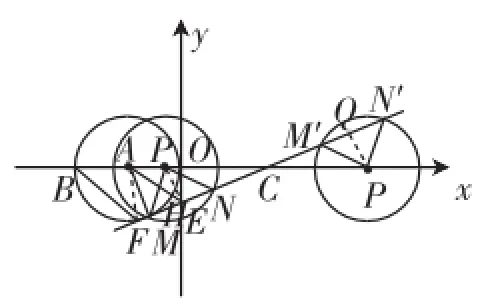
图9
解析:(1)略.
(3)存在,当点P在点C左侧时,若∠MPN=90°,过点P作PH⊥MN于点H,易证△CPH∽△CAF,点P在点C右侧时,记为P′,设∠M′P′N′=90°,过点P′作P′Q⊥M′N′于点Q,则P′Q=P′Q=PH,可知P′与P关于点C中心对称,根据对故存在这样的点P,使得△PMN为直角三角形,P点坐标
说明:本例一方面考查学生综合运用知识解决问题的能力,另一方面让学生感受到“通法”的力量,很多难题都是通过转化为基本题目或基本方法(通法)来解决的.本例中第(3)问难度较大,但解题思路正常,不强调技巧,在顺利解答前面的问题后,充分利用第(1)、(2)问的结论和思路,第(3)问的解决顺理成章.
三、几点思考
例题教学以“题目串”的形式展开为好,让不同的例题承载不同的作用,相互结合,共同发挥教育功效.例题设计既要注重知识关联,又要注重能力发展;既要归纳解题方法,更要提炼数学思想;既要突出教学重点,也要关注中考热点.
1.知识与能力并重
设计“题目串”要起点低,坡度小,图形简单,但知识点的容量大,便于学生系统建构知识体系,感悟解题方法,培养解题能力,做到知识与能力并重.例1的设计以知识梳理为主,为解答题目做相关知识准备,例3的第(3)问利用临界位置(或特殊位置)求参数的取值范围,这一设计不仅考查了等腰三角形的性质、矩形的性质、圆的知识,同时也培养了学生的空间想象能力.这些题目的设计不仅体现了数学知识、技能、经验的内在价值,更突出了对学生运用这些知识的能力培养.
2.思想与方法兼顾
利用典型例题教学,不仅能使学生获得基础知识和基本技能,更能掌握解题“通法”,深化数学思维.例2创设的“三轮车上楼”这一生活背景,既体现了“数学模型”思想,让学生感受到数学来源于生活,又归纳出解答本章习题的“通法”,即构造“相似三角形和勾股定理”.例3通过求参数的取值范围提炼出运动模型,并借助特殊位置巧妙解题.例4通过分类讨论,让需要考虑的点(位置)不漏不重,并顺势提炼出分类思想.上述设计不仅使学生获得了解题方法,更培养了学生的思维能力,收获了数学思想,真正做到了思想和方法的兼顾.
3.重点与热点并行
重点知识是一章的核心知识,它既是学习的重点,也是考试的重点.围绕核心知识,不仅要注重知识的建构,更要加强相关题型的归纳.热点题型就是结合生活背景,注入时尚元素,综合各章知识的综合题,旨在引导学生关注生活、关注社会、灵活运用所学知识和方法去解决问题,教师一定要关注重点和热点题型,加强对这些题目的研究和总结,以适应课标和社会需要“.切线的性质与判断定理”是本章的重点知识,笔者在4个例题中均有体现,并渐次深化对该知识的认识,不断归纳切线的解题方法.同时,对生活中的“三轮车上楼”、点的运动、参数变化范围、函数与圆的结合、圆与点的运动等热点题型均给予重视,所以,中考复习时,重点与热点并行,两者不可偏颇.
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
2.陈志勇.同步中考:二轮复习课的教学指向[J].中学数学(下),2015(1).
3.高之风.透视中考热点——动态问题的求解策略[J].中学数学(下),2013(1)
