模型归一理解本质——一堂市级公开课“等可能性”的教学设计

☉南师附中新城初中怡康街分校 李明顺

模型归一理解本质
——一堂市级公开课“等可能性”的教学设计

☉南师附中新城初中怡康街分校 李明顺

随着新课改的实施，各地的课堂教学有了很多的转变，但课堂教学中仍然存在一定的问题：其一，过程性认识偏浅——事实性现象和事实性知识之间缺少思想方法，缺少逻辑推理的联系、体验，探究活动存在着时间、空间引导与安排上的问题，虽然课堂在探索，但仅局限于浅层次的探索，并未获得该有的深层次结论，认识较浅；其二，课堂基于“题”的教学——缺少结构性迁移，教师在课堂教学中对题目的开放性要求不够，互动、自主设计、学习探究指导不足，故而解题教学过度，学生缺乏基本的经验，并未形成常规的思路，对于题目达不到举一反三，灵活解答.针对上述存在的问题，近期笔者在本市开设“等可能性”一课，旨在进行高效课堂的研究，受到一致好评，在此授课过程中有颇多感悟和收获，故撰文与同行交流.

一、对教学背景的理解

本节课是苏科版教材九年级第四章“等可能条件下的概率”第一节“等可能性”的内容.等可能性是初中阶段“概率与统计”体系中概率部分的重要内容.课本在编排时注重螺旋式的上升，从八年级的认识概率到了解随机事件的可能性有大有小，再到九年级试验的结果具有等可能性，逐层递进.本节课的学习是解决等可能条件下的概率的一个重要基础，只有正确地理解和掌握等可能性的相关知识，才能学好等可能条件下的概率.因此，等可能性的研究综合了前面学习过的认识概率的相关知识，同时又为后继的内容做了奠基，起到了承前启后的作用.

二、对教学的思考定位

《新课标》中明确指出数学在应用方面需要大力加强，鼓励学生发现数学的规律和问题解决的途径，使他们经历知识的形成过程，在数学课堂教学中揭示出知识的本质，让学生的数学思想得到发展，是目前数学教师刻不容缓的重要职责.

本节课的教学应依赖于实验作为认识的基础，对学生来说，“等可能性”的理解是全新的思维转型与挑战.纵观我国现行的主要的初中数学课标实验教材，从对“等可能性”的教学要求上看，要求不一，有的教材仅仅是几笔带过，而苏科版教材却用专门的一节进行学习，虽然本节课内容并不复杂，但它是解决等可能条件下的概率的一个重要基础，重要性不言而喻；从各套教材对“等可能性”的理解过程上看，都借助具体情境入手，在结合具体情境认识之后，进一步归纳其定义，这样更有利于从本质上认识等可能性的意义，而且九年级的学生也具备了相应的认识能力.

基于上述考虑，本节课的流程是先回顾随机事件的可能性有大有小，继而到试验结果具有等可能性，再到通过列举的结果不同使试验结果不具等可能性转变成具有等可能性.本节课的设计从学生熟知的情境出发，在情境的设计上尽可能多地举例子，如抛硬币、掷骰子、转转盘，使情境尽可能丰富，尽量包含形式多样的离散和连续的情境，之后在归纳其共同特征的过程中，让学生理解等可能性的概念，为了使学生对等可能性的理解更加透彻，适当补充试验的结果无穷多个下的等可能性，在学生理解了等可能性的意义后，可以进行对随机试验结果等可能性的判断，最终让学生自己设计一个游戏，并说出可能出现的结果，使其每个出现的结果具有等可能性.

三、教学目标的定位

（1）会列出一些类型的随机试验的所有可能出现的结果（基本事件）.

（2）理解等可能的意义，会根据随机试验结果的对称性或均衡性判断试验结果是否具有等可能性.

（3）在理解等可能的意义及其运用的过程中，体会分析问题的方法，积累数学活动的经验.

四、教学重难点的定位

重点：理解等可能概念的意义，会根据随机试验结果的对称性或均衡性判断试验结果是否具有等可能性.

难点：理解等可能概念的意义，会列出一些类型的随机试验的所有可能出现的结果.

五、教学过程

环节1——情境引入

播放2015年8月13日东方卫视真人秀《我去上学啦》片段.

分析：众所周知，近期各大电视台真人秀节目百花齐放，学生是其重要的收视群体，故以电视上某真人秀节目中的片段入手，可以贴近学生的日常生活，消除学生刚上课的不适应感，同时通过视频的观看可以让学生复习事件的3种类型：随机事件、必然事件、不可能事件，为下面的学习做铺垫.

环节2——实践探索

探索一：一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后从中任意摸出一个球，摸到白球与摸到红球的可能性一样吗？

探索二：（1）抛掷一枚均匀的硬币1次，硬币落地.①落地后有几种可能的结果？它们都是随机事件吗？②每次试验有几个结果出现？每次试验有第二个结果出现吗？

③每个结果出现的机会均等吗？

（2）在3张相同的小纸条上分别标上1、2、3这3个号码，做成3支签，并放在一个不透明的盒子中搅匀，从中任意抽出1支签，会出现哪些可能的结果？这些结果出现的可能性一样吗？

（3）如图1，一个可以自由转动的转盘，它被分成3个相等的扇形.任意转动转盘，当转盘停止转动时，指针落在三种颜色区域上的可能性一样吗？（指针指向两个扇形的交线时，当作指向右边的扇形）

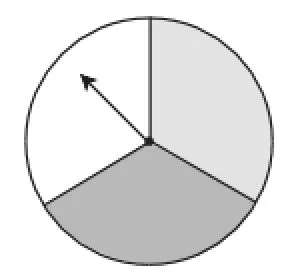
图1

（4）一枚质地均匀的骰子，6个面上分别标有1～6这6个点数，任意抛掷1次.从结果的角度分析，你能说出哪些正确的结论？

探索三：如图2，当转盘停止转动时，指针指向的位置有多少种可能的结果？

图2

分析：探索一通过摸球的试验，复习八年级知识，让学生体会随机事件发生的可能性有大有小，此处的设计正好为探索二试验的结果具有等可能性形成鲜明对比.探索二的4个问题环环相扣，问法也在逐层提高要求，先以选择入手，难度低，容易上手，再以问答形式入手，难度增加，最后开放性较大，让学生从结果的角度分析，说出正确的结论，探索二的4个问题可谓相当精妙，让不同层次的学生都能有回答的机会.探索三将探索二中转盘的问题加以适当改变，归纳出试验结果无穷多个情况下的等可能性.三组探索，有连续、有离散，让学生充分感悟事件的等可能性与不等可能性，为后续学习奠定基础.

环节3——数学认识

结论1：一般地，随机事件发生的可能性有大有小．

结论2：一般地，设一个试验的所有可能发生的结果有n个，它们都是随机事件，每次试验有且只有其中的一个结果出现，而且每个结果出现的机会均等，那么我们说这n个事件的发生是等可能的，也称这个试验的结果具有等可能性．

结论3：一般地，如果一个试验的所有可能发生的结果有无穷多个，每次只出现其中的某个结果，而且每个结果出现的机会都一样，那么我们就称这个试验的结果具有等可能性．

升华：只有具备哪几个特征的试验结果才具有等可能性？

分析：先从丰富的探索中提炼出等可能性的基本特征，再让学生通过充分交流、讨论、探究，深化对等可能意义的理解，发展学生的数学能力，最终再将概念升华，提取出关键的本质.

环节4——课堂练习

辨析：（1）从一副充分洗匀的扑克牌中任抽一张，抽出5和抽出王是等可能的．（）

（2）一个装有除颜色外都相同的红、白、蓝三支竹签的不透明盒子，从中任意抽出一支签，抽到三种颜色签是等可能的．（）

再认识：一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后从中任意摸出一个球，会出现哪些可能的结果？

分析：再度体验探索一的问题，让学生认识到试验结果的选择不同，会出现不同的可能性，同时感悟模型之间的内在联系，加深对等可能性的理解．

练习题：

（1）班主任从一名男生和两名女生中任选一名学生，帮助学校图书馆整理图书，会有哪些可能的结果？它们是等可能的吗？

（2）A、B两地之间的电缆有一处断点.断点出现在各个位置的可能性相同吗？

（3）如图3，一个质地均匀的正十二面体，12个面上分别标有1～12这12个整数，抛掷这个正十二面体1次．

图3

①朝上一面的数会有哪些？它们发生的可能性相同吗？

②朝上一面的数是奇数与朝上一面的数是偶数，发生的可能性相同吗？

③朝上一面的数是4的倍数与朝上一面的数是6的倍数，发生的可能性相同吗？

分析：练习题讲解，给予学生正确的答题规范格式，特别要强调注重对事件描述的完整性的叙述.

环节5——能力拓展

设计一个游戏，并说出可能出现的结果，使其每个出现的结果具有等可能性.

分析：设置开放性问题，让学生尝试举例，感悟事件结果的等可能，加强对事件结果等可能性的理解．

六、教学反思

“当数学和学生的现实生活密切结合时，数学才是鲜活的、富有生命力的，才能激发学生学习和解决数学问题的兴趣”．本节课以学生熟悉的真人秀节目引入学习主题，再通过一个又一个的例子让学生领悟到学习数学的必要性，并让学生亲自体验用数学知识解决实际问题的过程．一方面，让学生经历将一些实际问题抽象为数学问题的过程，体会数学在实际生活中的应用，数学是应用的数学，培养学生利用所学知识解决实际问题的能力；另一方面，培养学生积极思考，积极应用所学知识解决问题的好习惯，渗透分类思想、转化思想、归纳意识和应用意识．

本节课的精华之处就在于以一个又一个生活情境入手，看似多而乱，实则清晰无比，通过一开始众多例子的不确定性到之后的具有规律性，让学生抽象出等可能的概念，用一个词形容：模型归一，众多等可能模型最终实现归一，凸显出此处的数学本质．故笔者认为课堂如何高效，必须“探”其本质，“究”其思想，想要一节课让学生有所收获，不仅仅是知识层面的，还要有思想层面的收获，所以课堂一定要让学生多去探索、归纳，提炼数学的思想，最终理解本质内容．H