一道“最值”试题的讲评历程与教学启示

●崔道永(沛县中学江苏沛县221600)

一道“最值”试题的讲评历程与教学启示

●崔道永(沛县中学江苏沛县221600)

高三数学一轮复习常以试题为载体，试题可以选取千锤百炼的经典试题，也可以选取富有变化的创新试题，但选取的原则都要具有夯实基础知识、熟练基本技能、贯通基本思想方法的功能，教学中应该挖掘试题本身的价值以提高复习的有效性.最值问题在高考中出现的频率较高，常常受到命题专家的青睐，现笔者以讲解一道最值问题时出现的一个片段为例，谈谈对高三数学复习课的一些看法，不当之处望同行指正.

1 试题呈现

例1若实数x，y满足x2+y2=2(x+y)，则x+y的最大值为______.

2 教学实录

师:观察试题结构，如何处理?

生1:运用基本不等式进行放缩，从而构建关于x+y的不等式?

师:如何构建?

生1:条件x2+y2=2(x+y)可化为(x+y)2－2(x+y)=2xy，运用基本不等式，得

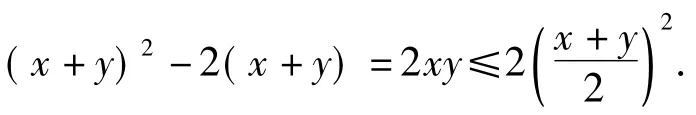
令x+y=t，可得

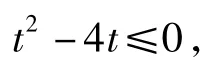
易得tmax=4.

师:很具体.还有其他思路吗?

(小组活动，时间5分钟.)

设计意图这里通过对试题表征的观察，让学生掌握解决此类题目的通性通法(其实通性通法在应试中才是学生致胜的法宝).接着教师又抛出问题“还有其他思路吗?”促进学生进一步观察试题.通过小组合作交流、探究问题可以帮助基础较差的学生查漏补缺，通过合作研究新思路、新解法也可促进并提高学生思维的灵活性与广阔性.

设计意图继续巩固平方平均数与代数平均数、几何平均数、调和平均数的关系，以及基本不等式等重要的不等式模型，加深学生利用这些不等式模型构造不等关系的理解.

师:审视条件x2+y2=2(x+y)，我们能联想到什么?看结论x+y的特点再联想，我们在什么情况下经常碰到?

生3:令x+y=t，可以采取线性规划的方法:满足条件的点(x，y)均在以(1，1)为圆心、为半径的圆上，而目标函数可化为y=－x+t，其中t的几何意义为直线在y轴上的截距，最优解就是动直线与圆相切时2个切点中的一个.

生4:x2+y2=2(x+y)可化为

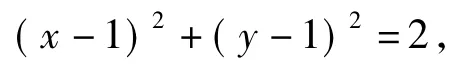
不难求得其最大值为4.

师:生3是从数形结合的角度研究最值，生4则是从函数的角度研究最值，很好!但从科学的角度来说，线性规划是建立在线性的可行域与线性的目标函数之上，在这里不能称“线性规划的方法”，而是采用了“线性规划的思想”.

(生3、生4板书过程，全体学生查漏补缺，时间5分钟.)

师:大家能否总结与点评本题的解题思想?

生5:解决最值问题常用的方法有函数思想、基本不等式、直接或间接建构不等式、数形结合等，我们还应该注意隐含条件的发掘与使用.

(学生自主整理1分钟.)

师:很好!下面看变式练习.

生6:受生3的启发，我还有另一种方法:x+ y=t可变形为

代入x2+y2=2(x+y)，得

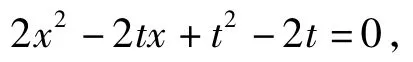
令判别式Δ=4t2－4×2(t2－2t)≥0，也可求得t的最大值为4.

点评1)对问题的表征能力是学生需要周而复始磨练的主要能力，不仅仅是简单地对条件与结论的分析，更重要的是不断地参与和积累;2)教学不是简单地重复，也不是机械地罗列，分析完一道试题的表征与解法不要直接进行下一题，要给学生留出短暂的时间内化(该课中，教师故意留出1分钟，这可以形成一种习惯，而我们经常看到许多教师讲完第1题紧接着第2题、第3题，久而久之学生会变成呆板的解题工具而缺乏灵气);3)让学生自主探究并总结问题的主要思想方法等核心内容，对提升学生的问题迁移能力意义深远(生5将解决最值问题的方法进行了梳理，本身就是对知识体系的补充与完善);4)教学过程不可操之过急，否则学生会失去自我表现的机会(生6在教师要进入下一环节时补充了判别式法，虽然不常用但让我们眼前为之一亮).因此，不要小看学生的能力，更不要吝惜课堂上看似宝贵的45分钟，让学生尽情地发挥.这样的课堂容量不一定小!

变式练习已知x＞0，y＞0，且满足x+3y+ xy=9，求x+3y的最小值.

设计意图无论是复习课中的巩固性练习还是试卷讲评课中的补救性练习都是深化知识的必要步骤.简单的就题论题当时有一些作用，但会随着时间的流逝遗忘殆尽，而变式练习作为加深问题理解的主要形式，不要仅仅局限于简单的数字与字母变化，应有一定的梯度且能暴露重点、难点、易错点，否则就不能刺激学生对问题的二次理解.变式练习的设计可以是正向的也可以是逆向的，甚至可将题目的条件与结论均作适当调整，只要能反映相似或相关的思想方法即可.

师:观察本题如何解决? (小组合作交流5分钟.)生7:x+3y+xy=9可化为

令x+3y=t，得

可求出x+3y的最小值为6.

师:用基本不等式配凑时需要简单的系数变换，很好!还有吗?

师:“三相等”满足吗?

生8:应该吧!

师:不能妄加推断，哪位学生帮帮他?

生10:借鉴生8的解法，还能利用导数法:令

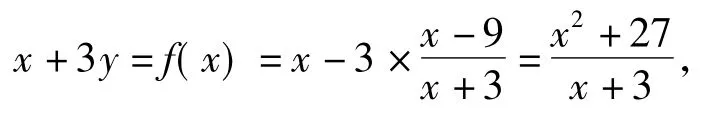
最小值应该在函数的极小值点处取得，但生9求变量的范围不可省略.

(生8、生10通过板演检验解法的可行性，时间5分钟.)

点评通过例1的教学过程，学生基本掌握了求最值的常用方法，收获了对隐含条件深究的意识，甚至还轻松地发现了解决超越函数最值的常用方法——导数.部分学生对该问题的认识比较到位，同时其他学生开阔了视野并拓宽了思路.

生11:作为生7的补充:x+3y+xy=9也可变形为

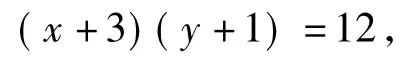
在“乘积一定”的条件下，如何将x+3y变形，再利用“乘积一定，和最小”呢?

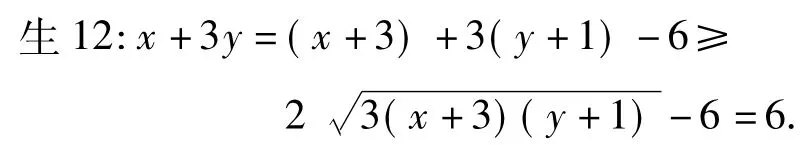
点评将x+3y+xy=9变形为(x+3)(y+ 1)=12属于逆向思维，该方法难度大，同时将x+ 3y配凑为(x+3)+3(y+1)－6也需要一定的基础.生11向大家提出的问题是本节课的一次质的飞跃，他代替教师进行了提问、启发、点拨，最终使问题得以圆满解决.

3 教学启示

3.1 教学中教师的角色应该发生转变

“如何提高数学教学的实效”对每一个数学教育工作者来说都是永恒的话题.随着课改的实施，数学教学的方式方法发生了翻天覆地的变化，以适应时代对高中学生越来越严格的知识与能力要求.通过以“学生为主体，教师为主导”为指导方针的自主学习方式进行知识建构，能逐步帮助学生内化知识、提高能力、提升素养，同时也必然会成为切合实际的有效教学方式.

2013年，江苏省徐州市教育局以政府行为在全市各中小学大力推进“学进去，讲出来”的教学模式(简称“学讲方式”)，取得了有目共睹的实效，其意义就是加大学生活动的自主性，要求学生积极参与到活动中来，通过小组合作交流不仅自己学会而且能讲给别人听.有专家认为最高层次的教学是教师不讲(如果受学生基础等因素的制约一时做不到也应该少讲而不是越俎代庖)，只有将时间还给学生，通过不断地边学边讲必然会使他们由“学会”走向“会学”.

本节课的教学片段源于高三基本不等式的专题复习，在此之前学生对最值问题已经有了整体的认知基础.在这里，教师仅仅扮演引路人的角色，同时不同层次的学生均得到进步的快乐.由此可见，将课堂还给学生并通过师生、生生之间的提问、交流，不仅可以加深对问题的理解，还可以培养学生思维的深刻性、灵活性、广阔性、批判性.

一道例题及一道变式练习在传统式的教学框架下估计10分针就可以完成，而本节课学生活动则花去了大半时间，很多教师认为这样会耽误教学进度，但仔细回想，活动性强的课或许更有意义.记得多年前的一次经历:期中考试前一天模拟试卷评讲的一道原题在第二天的期中考试中出现了，而该题的得分率远远低出预期的估计.这说明传统、机械的“教师讲、学生听”在一定程度上效率不高，相反看似费时费力的活动课效率也不一定低，因为后者学生通过自己动手、动脑后有真真切切的收获.当然这里让课堂慢下来不是消极地慢也不是机械地等待，而是教师要把功夫花在研究上，使课堂更有活力.

3.2 高三复习选择的试题应以点带面——认真选取“骨架题”

低档题、中档题及难题在高考中的比例为4∶4∶2，由此可见80%的内容为难度不大的基础知识.如何掌握这些知识并融会贯通?在高三复习的过程中，或许学生应该用大量时间反复锤炼试题，但教师不得不思考一个问题:很多高三学生在经历高一、高二及高三的一轮、二轮、三轮甚至更多轮的复习不知做了多少套模拟、全真试题;经历了多少次调研、质检考试;用了多少本参考书，试题做了不下几万道，但在20多道高考试题面前还是显得力不从心，为什么功夫与效果不成正比?为什么量变没有引起质变?我们是否夸大了题海战术的作用?减负增效的出路何在?

在典型试题的框架下挖掘试题的价值并通过反复的打磨加工，通过少量的试题让学习变得有意义更轻松，选取“骨架题”越来越成为大家的共识.所谓骨架题就是那些与骨架内容(重要概念、公式)相关的试题，选取骨架题难度不一定要大，只要它们能客观地反映问题解决的内容、思想、方法即可，这一学习的目的在于把握整体的骨架.其实，很多课本上的试题都可作为骨架题的素材，课程标准对基础题就有略高于课本甚至来源于课本的要求.

本文的例1及它的变式练习反映了解决最值问题几乎所有的方法，即:函数思想、不等式、数形结合，不仅巩固了之前复习过的简单函数的最值、导数、线性规划等内容，还加深了对基本不等式及重要不等式的认知，在高三后期复习中意义更重要.为此，教师可以编制为数不多的几道试题，还可以选取简单的填空、判断、选择题等，不必拘泥于形式，让学生感觉负担不重、有意义、对高考更有指向性，长期坚持可以使学生对知识的来龙去脉更清晰，对问题解决的思想方法认识更透彻，对问题的表征能力、迁移能力更强化.

意大利经济学家巴莱多发现了著名的“二八定律”，其内容是:任何事物中最重要的、起决定性的只占20%，其余的80%却是次要的、非决定性的.数学教学应重视那宝贵的20%有决定性的骨架内容，骨架题可以将骨架内容串联起来，这样可以真正避免过度教学，实现减负增效.

3.3 形成机制，长效滚动

艾宾浩斯遗忘曲线告诉我们:随着时间的流逝，记忆也呈现有规律的变化趋势.因此，数学教学需要一种长效的机制不断地刺激学生的思维，而滚动练习就是效果明显的教学策略之一.所谓滚动练习，就是在正常的教学计划的基础上，每过一个时间段进行复习、提高的训练.现在的高三复习往往都是一个专题接一个专题，到考试时来一个突击复习，很多教师抱怨学生把讲过的内容还给了自己.如果能做到有效设计滚动练习，那么学生不至于只记住刚讲过的内容.

1)在下一专题复习时，不断注意与上一个或几个专题的联系，给学生留有足够的时间探究问题的不同解法，不仅可以发现新知，更重要的是还能巩固旧知.通过一题多变、一题多解、多题一解，最终实现多题归一并形成网络.

2)高三的数学复习紧张而有节奏，很多内容高考的要求很简单，但要靠学生不断地练习形成感觉，针对这些内容采取长效滚动也会提高教学的效率.如果在学习的过程中按阶段不停地有规律地进行数量不多、难度不大的专题滚动练习，再经历系统复习的磨练，这些问题可能已不再是问题，也将为高考打下更坚实的基础.