运动船舶磁性船体产生的感应电场*

张伽伟，熊 露，龚沈光

(1．海军工程大学兵器工程系，湖北 武汉 430033;2．军械士官学校 雷达系，湖北武汉 430075)

船舶电场是除声场、磁场、水压场外最重要的水中目标特性之一［1］，目前已有许多关于船舶的轴频电场研究［2-5］，也有部分关于金属船体运动产生的感应电场研究［6］。由于船舶一般都是由钢铁等铁磁性材料制造，船舶在航行过程中受地磁场感应磁化而形成感应磁性，由于船体具有磁性，所以当它航行时会引起空间磁通的变化而产生感应电场，因此对运动磁性船体产生的感应电场信号特征进行研究，可以完善和深入研究船舶电场信号的产生机理和分布特征，有利于船舶的探测和隐身技术的研究。

原子磁矩作为磁性物体的最小单元，可以通过组合叠加等效任何磁性物体的空间磁场。在以往的研究中，已经提出了利用位于船体内的若干磁偶极子和旋转椭球体的混合阵列可以等效舰船的空间磁场。国内在对运动磁偶极子的感应电场建模时采用了两种方法:一是利用法拉第电磁感应定律，通过选取恰当的环路积分计算出空间中的感应电场［7］;二是通过变换参考系，采用相对论电磁变换，利用v×B计算运动磁偶极子的感应电场［8］。对于环路积分，首先假设了积分环路上的电场强度处处相等，此假设只在磁性物体沿着磁矩方向运动时才成立，因此当运动方向不一致时，环路积分存在较大近似误差;对于v×B适用于磁性物体沿任意方向运动，但是忽略了介质对电磁场的影响，当磁性物体在导电介质中运动时，由于电场和磁场的相互激励作用磁性物体在沿运动方向也会产生感应电场，使得此方法也不能够准确反应磁偶极子运动产生的感应电场。国外对磁偶极子运动产生的感应电场利用研究则主要是求解麦克斯韦方程组，推导在介质中磁矩和电矩之间的转换关系，从而得到运动磁偶极子的感应电场和运动电偶极子的感应磁场［9-13］，但都是处于理论研究，未进行实验验证。张伽伟等采用库仑定律、毕奥-沙伐定律和麦克斯韦方程组等基础理论求解适用于介质中任意方向运动磁偶极子所产生的感应电场并进行实验验证，进一步得到运动船舶磁性船体产生的感应电场模型。

1 磁偶极子运动产生的感应电场

1．1 磁偶极子运动产生的电场模型

考虑具有恒定磁矩的磁性点源在t时刻位于τ0=(x0，y0，z0)的位置，观测点的位置 τ=(x，y，z)，令向量 R=τ- τ0，R=|τ-τ0|，n=R/R，由库仑定律和毕奥-沙伐定律得到空间中磁偶极子所产生的电场和磁场强度为

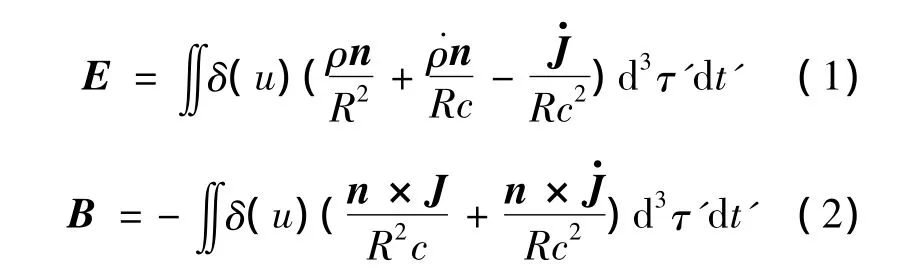
将ρ=0，J=c∇×M(M为磁偶极子的磁矩)代入式(1)、式(2)并化简可得

式(3)、式(4)构成的麦克斯韦方程组的解为

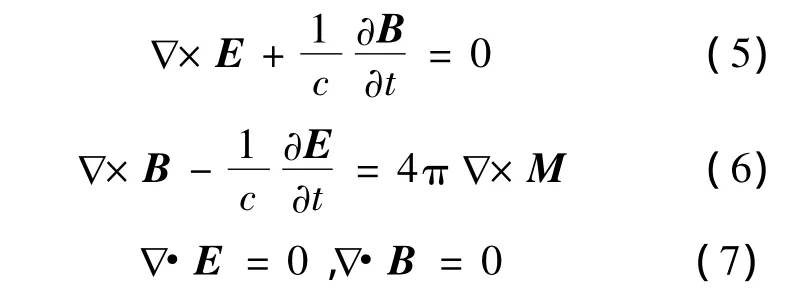
因为M是被限制在一个有限的区域中的，由式(3)、式(4)可以看出电场E和磁场B满足无限远处为零的条件，式(4)中的8πM/3为当前时刻场点处的场强，因此式(1)、式(2)是满足麦克斯韦方程组的。

当磁偶极子沿某一方向运动时，其磁矩可以表示为 M(τ，t)=Mδ［τ- τ(t)］，τ(t)表示 t时刻磁偶极子所在的位置向量，代入式(1)得到

有理论公式

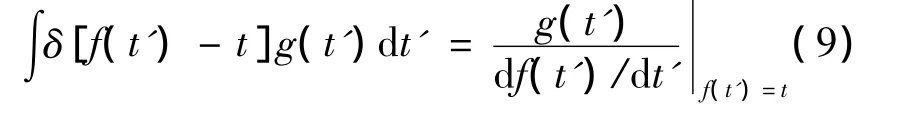
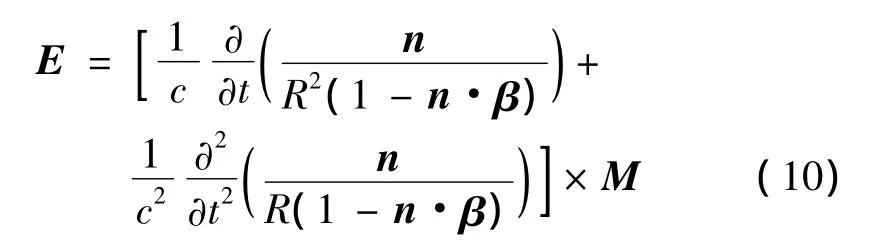
对式(10)求解得到运动磁偶极子的感应磁场最终表达式为

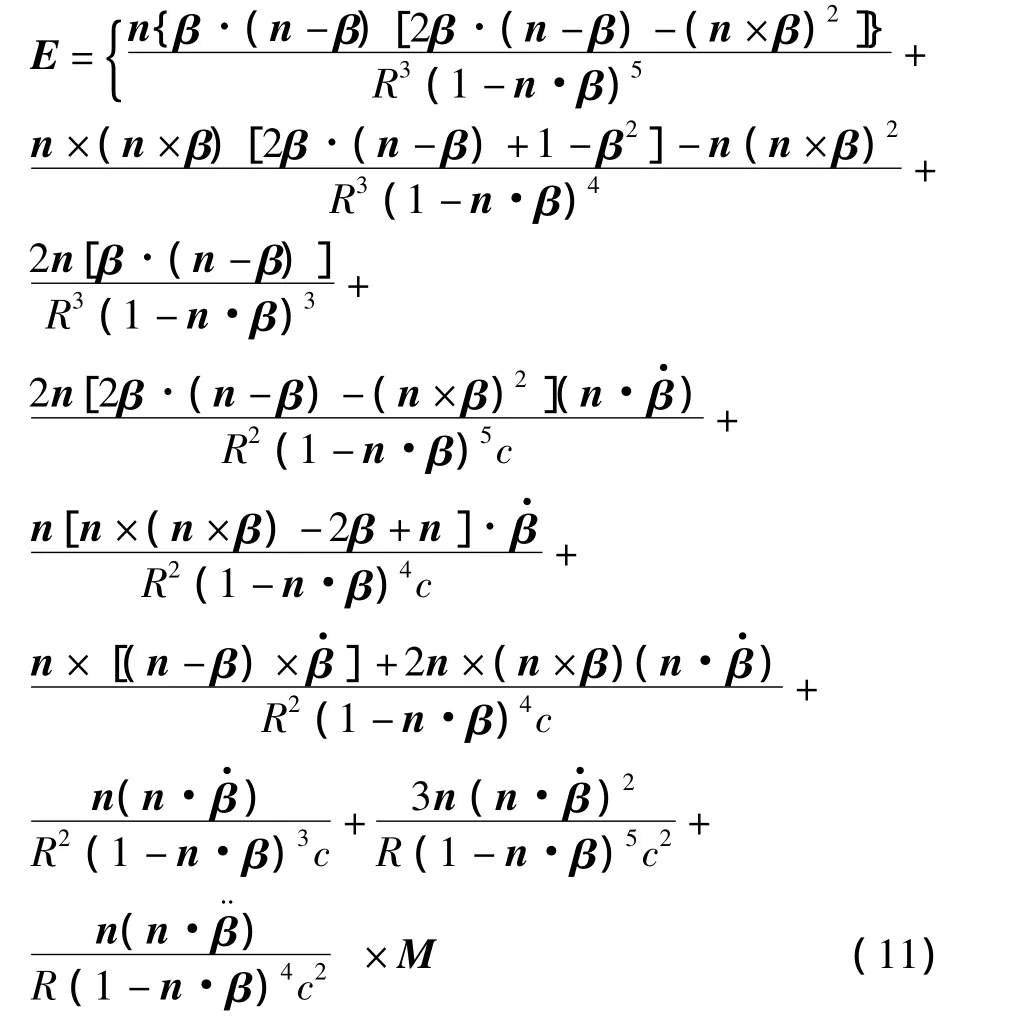
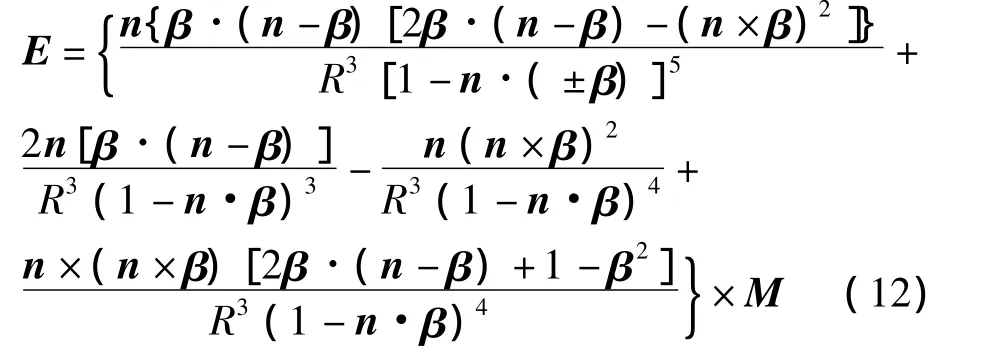
从磁偶极子感应电场的表达式(12)可以看出:感应电场强度E，随着离观测点的距离R是成3次方衰减的。

1．2 感应电场的仿真计算

考虑磁矩为M=1i+1j+1k(单位为A·m2)的磁偶极子从坐标原点出发 τ0=(0，0，0)，沿着 x式(8)得轴方向匀速运动，运动速度v=(1，0，0)m/s，需要注意的是式(12)为高斯单位制下的电场表达式，磁矩从国际单位A·m2到高斯单位需乘以，电场强度从高斯单位转换到国际单位要除以为真空磁导率，ε0=1/(36π×109)为真空的介电常数，仿真得到观测点(5，0，1)处的三轴通过特性如图1所示，由图1可知磁偶极子感应电场有明显的三轴通过特性，量级大小为0．1μV/m(感应电场大小与磁矩、运动速度和观测点位置有关)。

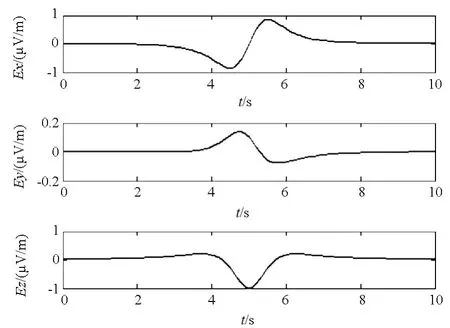
图1 磁偶极子通过特性Fig．1 Through characteristics ofmagnetic dipole

2 运动船舶磁性船体产生的感应电场

2．1 磁性船体产生的感应电场模型

采用磁偶极子和旋转椭球体的混合阵列等效磁性船体的磁场，可以结合旋转椭球体可拟合大范围磁场、个数少和磁偶极子局部磁场拟合精确的优点，不仅保证了模型的简单化和稳定性，而且还具有很高的拟合精度。现采用一个长轴等于船长，短轴等于船宽的均匀磁化旋转椭球体来拟合船舶的大范围磁场，用布于船舶中线上的一系列磁偶极子来拟合局部磁场(也可以是多条线的磁偶极子阵列，具体采用怎样的混合阵列模型，需要根据船舶的实际磁场测量值进行拟合)，混合阵列的模型如图2所示，该混合模型具有精度高、因子数少、稳定度高等特点。磁偶极子阵列中心为坐标原点，每个磁偶极子的磁矩分别为Mi，因磁偶极子数N为奇数或偶数时计算方法完全一样，假设N为奇数，在图3所示的坐标系中，第i个磁偶极子的坐标为

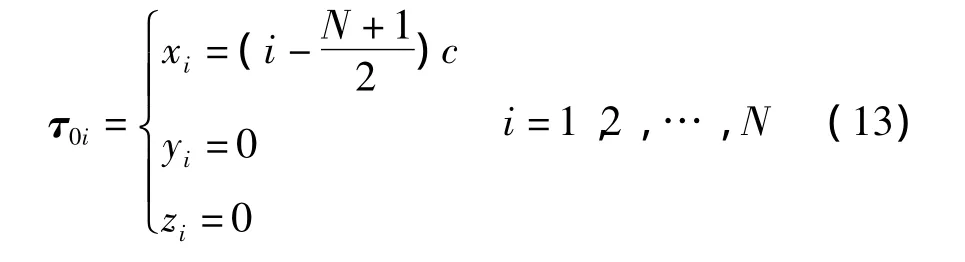
图2 磁性船体等效模型Fig．2 Equivalentmodel ofmagnetic ship

图3 磁偶极子阵列Fig．3 Magnetic dipole array

运动磁偶极子阵列在空间任意一点p(x，y，z)处产生的感应电场大小，为单个运动磁偶极子在该点产生的感应电场的叠加，所以根据式(12)可直接写出磁偶极子阵列的感应电场为

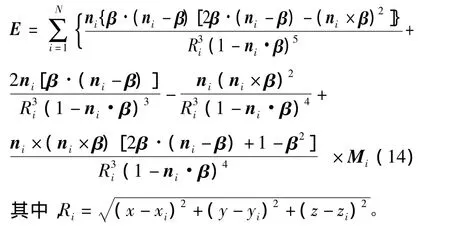
2．2 磁性船体感应电场实例计算

根据的磁性船体的混合阵列模型，用单线磁偶极子阵列和一个旋转椭球体对船舶磁场进行建模，对一条长为100m船舶的实测磁场数据进行拟合反演，得到18个磁偶极子和一个旋转椭球体的磁矩及其坐标如表1所示，表中第19组数据为椭球体的数据。

将计算得到的船舶磁矩，代入磁性船体运动的感应电场模型式(14)，并令船舶航行速度为10m/s，进行实例仿真计算，图4～6为在水下20m处，感应电场的三轴分量沿着船舶前进的方向和正横方向的空间分布，图7为感应电场合场强在水下20m处的空间分布图。由图4～7可知，磁性船体运动产生的感应电场具有明显的空间分布，区域性较强，在船身附近有明显的峰值，合场强在水深20m处最大可达1mV/m。

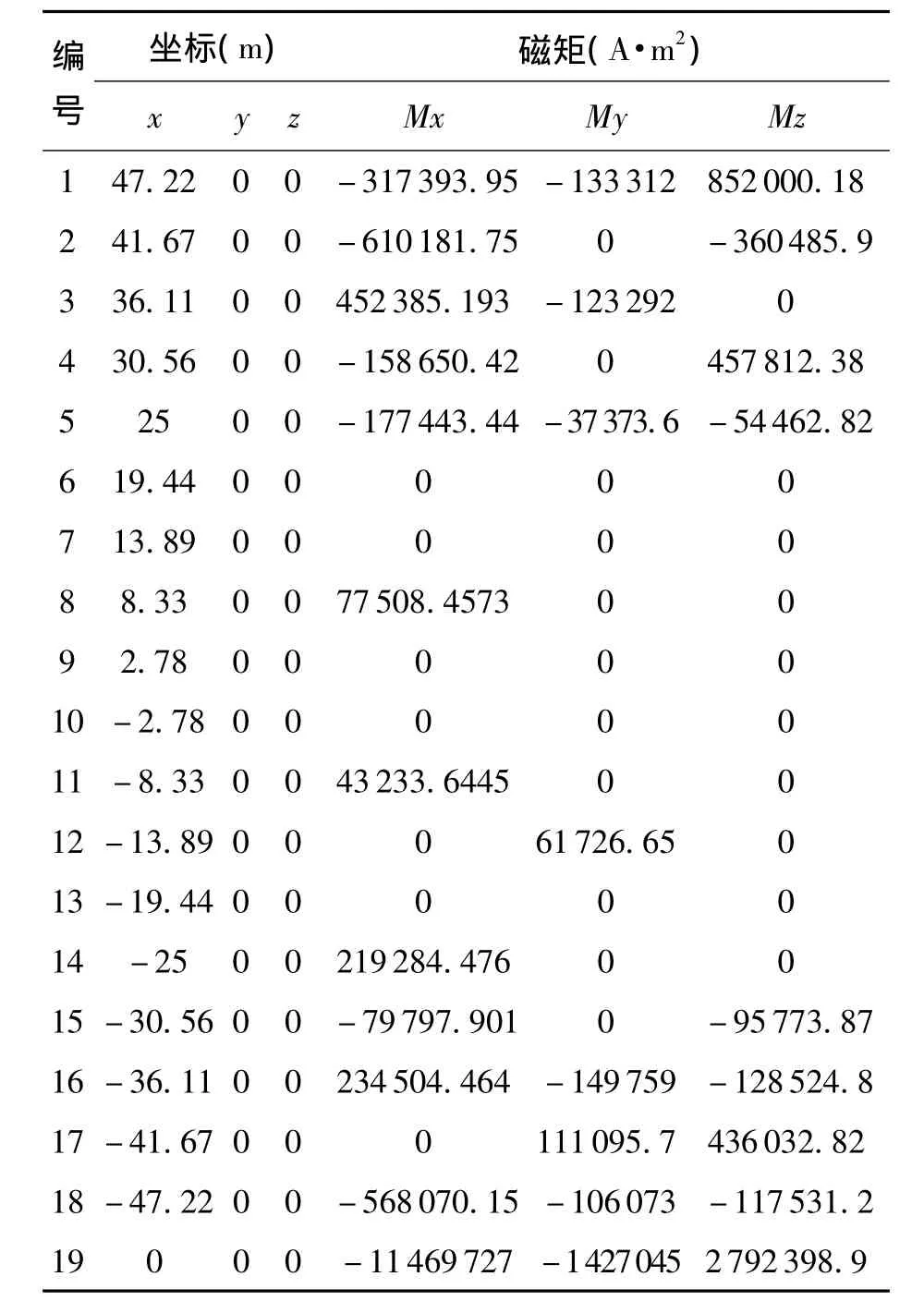
表1 磁性船体混合阵列磁矩大小及坐标Tab．1 Mixture array ofmagnetic ship

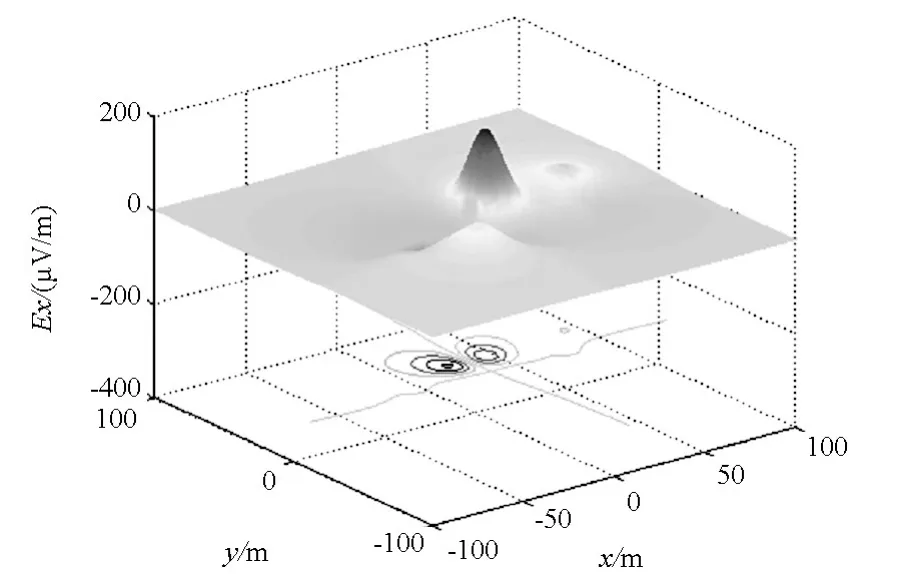
图4 20m水深下的E x的空间分布Fig．4 Spatial distribution of E x

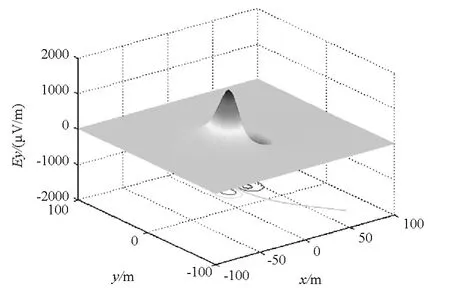
图5 20m水深下的E y的空间分布Fig．5 Spatial distribution of E y

图6 20m水深下的E z的空间分布Fig．6 Spatial distribution of E z

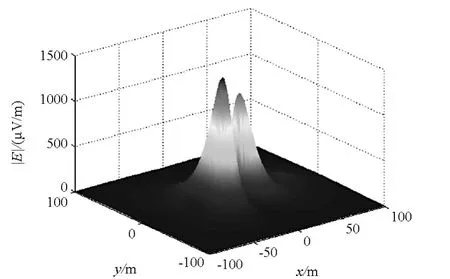
图7 20m水深下的E的空间分布Fig．7 Spatial distribution of E

3 实验验证

由于船舶磁场可以用若干个位于船体内的磁偶极子和旋转椭球体磁场的线性叠加来等效，因此验证磁性船体运动产生感应电场数学模型的正确性，关键在于验证运动磁偶极子产生的感应电场计算模型。

实验采用一块条形强磁铁等效磁偶极子，用银-氯化银电极组成的测量系统，在海水中选取测量点测量海水中产生的感应电场。所得到的电场信号经过放大滤波后，使用数据采集卡采集、存储和显示。

以上述强磁铁等效磁偶极子，实验室水池水深为90cm，测量系统所在深度为40cm，电导率为0．4S/m，三个方向测量电极与参考电极之间的电极距分别为 x-o=10cm，y-o=30cm，z-o=20cm，磁铁离测量系统参考电极的正横距y=15cm，相对高度z=15cm(即磁铁在水中拖动)，磁铁沿x轴匀速拖动，拖动速度约为0．5m/s，测量电极信号经过滤波和1000倍放大后送到数据采集卡，采集卡采样频率fs=40Hz。图8为磁铁正向匀速运动时实测的感应电场三轴通过特性，图9为磁铁正向运动时电场模型仿真结果，图10为磁铁反向匀速运动时实测的感应电场三轴通过特性，图11为磁铁反向运动时电场模型仿真结果。磁铁正向运动时，在5．5s左右通过测量系统，磁铁反向运动时，在7s附近通过测量系统，通过图8～11可以得到以下结论:

1)理论分析相同，磁偶极子沿着x方向匀速运动，在三个方向都会有感应电场分量产生，且通过特性明显，与采用相对论电磁变换v×B得到的在运动方向不会有电场分量是不一致的;

2)实测磁铁运动感应电场正向、反向运动的相位变化，以及三轴分量的相位关系均与理论仿真相吻合;

图8 磁铁正向运动时的感应电场Fig．8 Actual induced electric field ofmagnet moving in the posite direction

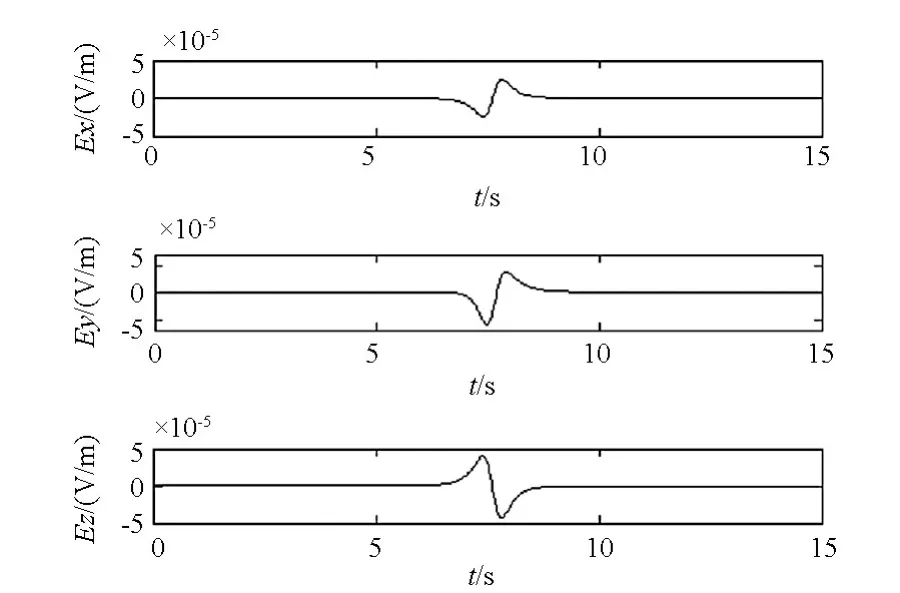
图9 正向运动时的理论值Fig．9 Theoretical value in positive direction

3)在量级大小上，仿真曲线与实测信号基本重合，正向运动时，实测感应电场的峰值分别为Ex，理论计算值为反向运动时，实测的峰值分别为，理论计算值为可知理论计算数据和实测数据在同一量级且大小基本一致。

图10 磁铁反向运动时的感应电场Fig．10 Actual induced electric field ofmagnet moving in the negative direction

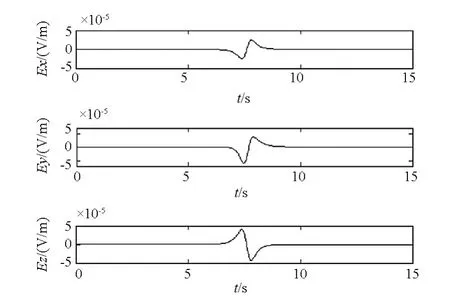
图11 反向运动时的理论值Fig．11 Theoretical value in negative direction

由于运动磁铁产生的感应电场十分微弱，且不能完全排除导线切割磁场对测量结果的影响，因此上述实验在量级和波形上与仿真结果基本一致，说明理论计算模型的正确性。

4 结论

本文研究了运动船舶磁体运动产生的感应电场，建立了感应电场的数学模型，通过实验和实例计算得到了以下结论:

1)磁偶极子运动产生的感应电场有明显的三轴通过特性，包括磁偶极子的运动方向，而并非相对论电磁变换得到的只有两个方向，实验室实验证明了理论模型的正确性;

2)感应电场大小与磁矩、运动速度和观测点位置有关，在磁偶极子附近有明显的峰值，在磁偶极子通过后感应电场迅速衰减;

3)船舶磁性船体运动产生的感应电场，在船舶附近感应电场可达1mV/m，达到了可探测的量级，感应电场按与船舶距离的3次方衰减。

References)

［1］ 林春生，龚沈光．舰船物理场［M］．北京:兵器工业出版社，2007．LIN Chunsheng， GONG Shenguang． Physical field of warship［M］．Beijing:Weapon Industry Press，2007．(in Chinese)

［2］ Hubbard JC，Brooks SH，Torrance B C．Practicalmeasures for reduction and management of the electromagnetic signatures of in-service surface ships and submarines［J］．Malmo Undersea Defence Technology，1996:64-65．

［3］ Zhang H P，Chen X G，Chen Y A，et al．Real-time suppression research of shaft-rate electric field based on the compensated negative potential［J］．Applied Mechanics and Materials，2014，527:197-200．

［4］ Razavi S，Salimi M，Shahbazi-Gahrouei D，et al．Extremely low-frequency electromagnetic field influences the survival and proliferation effect of human adipose derived stem cells［J］．Advanced Biomedical Research，2014，3:25．

［5］ Dymarkowski K，Uczciwek J．The extremely low frequency electromagnetic signature of the electric field of the ship［C］//Proceedings of Undersea Defence Technology，Washington:Nexus Media Limited，2001:1-6．

［6］ 陈聪，李定国，龚沈光．运动舰船静态电磁目标特性的综合建模方法［J］．海军工程大学学报，2009，21(3):33-37．CHEN Cong，LI Dingguo， GONG Shenguang． Synthetical modelingmethod for static electromagnetic characteristics of a moving ship［J］．Journal of Naval University of Engineering，2009，21(3):33-37．(in Chinese)

［7］ 陈聪，李定国．运动磁偶极子感应电场的理论和实验研究［J］．华中科技大学学报:自然科学版，2010，38(10):116-118．CHEN Cong，LI Dingguo．The experimental and theoretical research on the induced electric field by moving magnetic dipole［J］．Journal of Huazhong University of Science and Technology:Natural Science Edition，2010，38(10):116-118．(in Chinese)

［8］ 孙明．舰船感应电场和极低频电场研究［D］．武汉:海军工程大学，2003．SUN Ming．The induced electric field and extremely low frequency electric field of ships［D］．Wuhan:Naval University of Engineering，2003．(in Chinese)

［9］ Morley P D，Buettner D J．Instantaneous power radiated from magnetic dipole moments［J］．Astroparticle Physics，2015，62:7-11．

［10］ Adorno T C，Gitman D M，Shabad A E．Electric charge is a magnetic dipole when placed in a background magnetic field［J］．Physical Review D，2014，89(4):7504．

［11］ Kholmetskii A L， Missevitch O V， Yarman T．Electromagnetic energy of electric and magnetic dipoles［J］．Canadian Journal of Physics，2013，91(7):576-581．

［12］ Hnizdo V．Magnetic dipole moment of a moving electric dipole［J］．American Journal of Physics，2012，80(7):645-647．

［13］ Coïsson R． Electromagnetic interactions derived from potentials:charge and magnetic dipole［J］．Physics，2014(2):47-56．