研读数学教材的四个维度
2015-04-02张卫星
张卫星
数学教材是教师教的依据,也是学生学的对象,它承载着数学知识与技能、数学思想与方法、解题策略等人类文化的结晶。面对静态的数学教材,教师需要深入其中,把握实质,才能浅出,从而帮助学生学好数学。可以说,教师对数学教材的解读深度、准确度,制约着教学的有效性,决定着学生学习的成败。笔者始终认为,研读数学教材要从四个维度入手。
一、研读数学教材的纵向联系
数学教材中的每一节内容都不是单独存在的,它与前面的内容及后续的知识总是有着内在的联系,即纵向联系。因此,笔者认为研读数学教材的第一步就是要理清教材的前后联系。唯有如此,才能准确把握数学教学的起点及所要实现的目标,从而为后续教学做好铺垫。
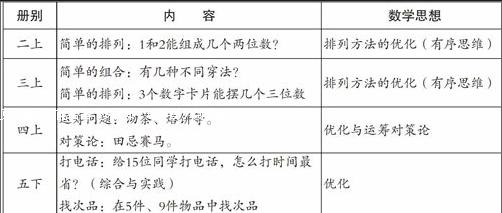
例如,“烙饼问题”是渗透优化思想的重要载体,学生通过学习会对优化思想有更深的认识。但优化思想并不是凭空产生的,它在小学数学教材中处处可见渗透的痕迹,如计算教学中的算法优化、解决问题教学中的策略优化以及统计教学中的统计方法优化等。除此之外,教材还以单元“数学广角”为呈现形式,较为集中地安排优化思想的渗透,具体分布如表1。
由表1可知,优化思想在四册教材中重复体现,呈螺旋上升趋势。在低年级,教材虽然没有将优化思想作为一节课的主要目标,但已经让学生对优化思想有了初步的体验。比如简单的排列,排列的方法有很多,但其中有序的排列可以做到不重复、不遗漏,学生初步体验到解决同一个问题有很多种方法,但诸多方法中有优劣之分,一个好的方法可以帮助我们更有效地解决问题。到了中高年级开始以优化思想作为一节课的主要目标展开教学,如“烙饼问题”和“找次品问题”的教学,它们都让学生经历了方法多样化和优化的过程,体验到了优化思想在解决问题中的应用价值,从而真正帮助学生形成优化思想。鉴于此,笔者认为此课教学的主要目标是让学生通过操作、模拟的过程,初步体会运筹思想在解决简单生活问题中的应用,从而形成寻找解决问题最优方案的意识。
由此可见,研读数学教材的纵向联系有利于体现数学教学的连贯性和新旧知识的关联,有利于学生准确把握教学目标,也有利于学生知识结构的纵向建构,能引领学生进一步思考和探索。
二、研读数学教材的横向联系
数学教材中的每一节内容既有纵向联系,又有横向联系。研读数学教材的横向联系,即研读新知识点与哪些知识是相似的,让学生及时横向沟通,领会新知识点更广泛的应用范围,从而达到以点带面的效果。笔者认为,研读数学教材是提高数学课堂教学效率的重中之重,不应忽视。
例如,“烙饼问题”并非为烙饼而烙饼,而是通过“烙饼问题”的学习提炼出相应的规律,从而去解决许多类似的问题。教材就为“烙饼问题”提供了三个相似的问题,意在加强知识的横向联系。
⒈教材105页“做一做”中的第二题:一种电脑小游戏,玩一局要5分钟,可以单人玩,也可以双人玩。小东和爸爸、妈妈一起玩,每人玩两局,至少需要多少分钟?
⒉教材107页的第二题:东东、晶晶和红红三位同学去量身高、验视力,每项检查要3分钟,他们至少要用多长时间才能做完这些检查?
⒊教材108页的第四题:三个客人去饭店吃饭,他们每人点了两个菜,假设两个厨师做每个菜的时间都相等,应该按怎样的顺序炒菜比较合理?
上述3个问题分别是玩游戏、体检和炒菜的实际问题,其解决原理和烙饼一样,学生只要掌握了烙饼实质,这三个问题就迎刃而解。而事实上与烙饼问题更为接近的问题有煎鱼、煎饼等生活化问题,为此,笔者在教学时设计了如下3个练习:
⒈妈妈用锅煎鱼,两面都要煎,一次能煎两条,煎一面要2分钟,请问妈妈煎完3条鱼至少要几分钟?
⒉妈妈用锅煎鱼,两面都要煎,一次能煎两条,煎一条鱼要4分钟(煎一面要2分钟),请问妈妈煎完4条鱼至少要几分钟?
⒊妈妈用锅煎饼,两面都要煎,一次能煎2张,煎一张饼要6分钟(每面要3分钟),请问妈妈煎5张饼至少要几分钟?
当然,解决这三个问题的前提是学生领会了“烙饼时间=烙饼张数×烙一面饼的时间”这一规律。由此可见,研读数学教材的横向联系有利于知识点的横向比较,体现同类知识点的关联,有利于学生知识结构的横向建构,能引领学生用类比的数学思想进行探究。
三、研读数学教材的公开信息
研读数学教材的公开信息,即研读教材展示的每一个文字和每一个符号,领会其中蕴含的数字信息。只有研读清楚教材的公开信息,才能理清教学的基本内容,才能为下一步的教学设计做好准备,这也是一位数学教师应该具备的最基本的技能。比较好的做法是:先梳理出教材展示的各种信息,然后决定各种信息的价值权重。只有这样,才能发挥教材的最大功能。
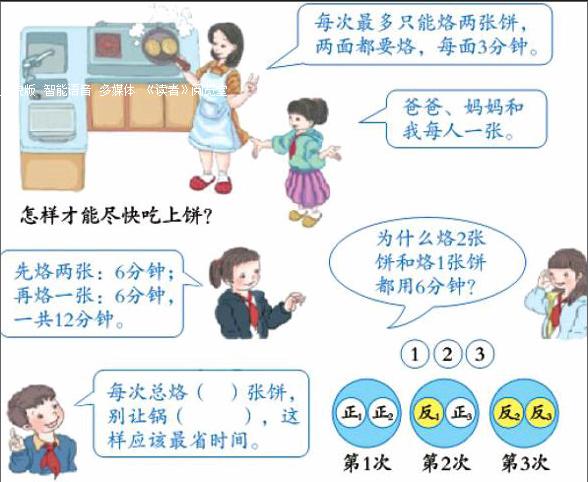
例如,“烙饼问题”的教材版面只有半面多一点(如图1),但其中蕴含的公开信息很丰富。笔者认为,它至少蕴含了如下5条公开信息:
⒈烙饼的条件:烙3张饼;每次最多只能烙2张饼;两面都要烙;每面要3分钟;尽快(时间最少)。这些条件表明了“烙饼问题”来源于生活。
⒉探索烙1张饼和2张饼的时间。探索时必须通过操作,让学生清楚烙1张饼和2张饼的时间。探索后还要引导学生比较所用的时间,从而让学生理解两张饼同时烙,没有让锅空着,充分利用了资源,比较省时间,而一张饼一张饼烙,浪费了资源,花的时间就多,这其实就是优化思想的核心所在。另外,先探索烙1张饼和2张饼的时间,其实是渗透了化归思想,即化难为易。
⒊探索烙3张饼的最少时间。“哪种方法比较合理?”教材中的一个反问表明烙3张饼的方法多样,应该组织学生探究。为了让学生思路更清晰,教材用示意图表示烙饼的过程。这就表明,在教学时理应让学生学会画示意图。同时,教材通过示意图展示出交替烙,让学生领悟其内涵,这比单纯的讲解效果要显著得多。
⒋探索烙4张饼、5张饼、6张饼……的最省时间。探索这么多时间,表明烙饼时要设计表格,只有这样,才能让学生的思维变得有序,也有利于后面的发现。
⒌“你发现了什么”表明教学时要提炼烙饼规律。
上述5条信息,教学时都要予以重视,但这5条信息中,笔者认为最重要的是第三条和第五条,第三条可以展示探索过程,也可以体现烙饼的实质,而第五条则可以简化烙饼规律,为知识的横向联系做好准备。可见,研读数学教材的公开信息,可以让学生准确把握教学的重点。
四、研读数学教材背后的秘密
研读数学教材背后的秘密,即研读教材蕴藏的知识点及思想方法。教材公开的信息,只要花点时间就能捕捉到,但发现其背后的秘密需要一定的教育经验与智慧。有经验与智慧的教师能准确捕捉到,没经验与智慧的教师就很难捕捉到。事实上,教材背后的秘密往往是决定一堂课能否成功的关键所在。因此,只有准确把握教材背后的秘密,才算把教材研读透了。
例如,“烙饼问题”教材除了展示出上述五条公开信息,它的背后还蕴含如下两条秘密:
⒈同时烙和交替烙的优势。同时烙,即同时烙两张饼的正面,再同时烙两张饼的反面。交替烙,即不一定同时烙两张饼的正面或反面,可能同时烙一张饼的正面和另一张饼的反面,也可能烙了一张饼的正面后,等一下再烙反面。但同时烙和交替烙有一个共同的优势,那就是让锅不空着,充分利用资源,从而让时间最省。事实上,偶数张饼适合同时烙,如2张、4张、6张等,奇数(除了1张饼和3张饼)张饼适合同时烙和交替烙同时使用,如5张饼,其中的2张适合同时烙,其余3张适合交替烙。因此,教师在教学时可以用表格展示出烙饼个数和烙饼时间,在此基础上引导学生去发现其中的奥秘。
⒉烙饼规律的实质。教学时,学生借助表格可以快速提炼出烙饼规律:烙饼时间=烙饼张数×3分钟,但教师还应该知道这个规律的数学实质。如教材上所说,烙3张饼的最省时间是9分钟,其实质是3张饼有6个面,每次烙2个面,需要烙3次(6÷2=3),每次3分钟,一共是9分钟(3×3=9)。当然,这个实质可以不告诉学生,因为告诉学生反而会把烙饼问题弄得更复杂,而且会冲淡先前的发现,但教师必须心中有底。从这个本质出发,教师在引导学生总结烙饼规律时,还可以再抽象一些,即3分钟是烙一次的时间,或者说是烙一面的时间,这样就可以提炼出一个更具普适性的规律:烙饼时间=烙饼张数×烙一次的时间或烙饼时间=烙饼张数×烙一面的时间。
由此可见,准确研读数学教材背后的秘密,可以让我们的数学课堂变得既有深度,又更简洁,这也许就是我们常说的深入浅出吧!
综上所述,当我们对“烙饼问题”的教材进行四个维度的研读后,对教材的定位就更准确,对教材的理解就更深刻,对教材的处理就更有针对性。可见准确、深度地研读数学教材,把握教材的意图,使教材的价值最大化,是教师步入高效课堂的第一步。
