利用数学教学中的一题多解，培养学生的数学思维

李家庆

数学思维一般是指能够根据客观条件的发展和变化，及时地改变先前的思维过程，寻找新的解决问题的途径。数学思维的灵活性，常表现在新知识的掌握、经验的积累、认识结构的改善、从已知关系中看出新关系、从隐蔽形式中分清实质等方面。因而数学思维的灵活性集中地反映在解题过程中。那么在数学例题教学过程中怎样应用一题多解、一题多变等手段培养学生数学思维的灵活性呢？我结合自己的教学实际谈几点看法。

一、例题教学中注重学生观察力的培养

例题是教材的重要组成部分，例题教学是课堂教学中的一个重要环节，它是使学生获得数学知识，掌握解题技能技巧，理解所涉及的数学思想方法，提高思维能力的主要渠道。教师在教学中应以本为本，以纲为纲，切实加强课本例题教学，培养学生的观察能力，从而训练学生思维的灵活性。

然后，两种方法加以比较，学生大惊：原来还可以这样做。

事实上，解题的灵活性是学生创造性学习的结果。而怎样做才能尽量地让学生进行创造性学习，到现在人们还无法给出一个固定的模式，很大程度上依赖于人们自己积累的富有创造性活动的经验。因此，在日常教学中我们采用的教学方法应有利于这种创造性经验的积累。这就要求我们教师在教学中从小处落笔，从细处抓起，引导学生认真细致地多观察，日积月累，从而培养学生的观察力、想象力，努力训练学生思维的灵活性。

二、一题多解，拓宽学生思路

在数学教学中，深入挖掘题目的条件，发现已知、未知之间的关系，多方位、多角度地观察和研究一个数学问题，寻求多种不同的解题思路和方法，是数学思维灵活性的重要标志，也是培养学生发散思维能力、拓宽思路、综合运用各种知识能力的重要标志和有效途径。一题多解，从解题目的来看，在于找到最有效的解题方法；从思维训练的角度来看，在于提高学生思维能力，培养学生良好的思维品质。

从以上几种解法中，我们看到：解法一是根据方程的根的“本来面目”来思考的，学生容易想到；解法二是从方程的根与系数的关系出发来考虑，它抓住了数学知识的内在联系；解法三则是从另一个角度来思考的，与解法二的一个共同特点是用整体的思想和方程的思想将看作一个整体k，则只要列出关于k的方程，通过解方程就可使问题得到解决。

因此，教学中，教师应充分发挥教科书例题的作用，启发学生积极思考，探索这些解题方法或证明方法，讲明这些方法是怎样想出来的。这对于学生融会贯通知识间的联系，综合运用各方面的知识，拓宽知识面，培养学生思维的灵活性大有帮助。

三、一题多变，培养学生思维的灵活性

“变”能使学生从不同角度考虑问题，发挥想象力、观察力，发现异同，从而改变解题思路和方法。所以，在教学过程中，对例题和习题的条件和结论进行某些交换，题目原有的解法也相应发生变化，这样的教学方法同样有利于培养学生思维的灵活性。

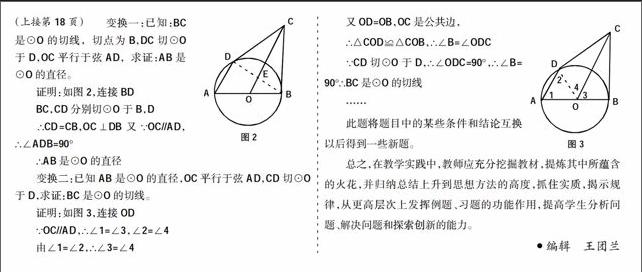
例3.已知，AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弘AD，求证：DC是⊙O的切线。

证法如下：如图1，连接OD，OA=OD ∴∠1=∠2

∵AD//OC ∴∠1=∠3 ∠2=∠4

∵∠3=∠4

∵OB=OD ∠3=∠4 OC=OC

∴△OBC≌△ODC

∴∠OBC=∠ODC

∵BC是⊙O的切线

∴∠OBC=90°∴∠ODC=90°

∴DC是⊙O的切线。

现将此题作如下几种变换：

变换一：已知：BC是⊙O的切线，切点为B，DC切⊙O于D，OC平行于弦AD，求证：AB是⊙O的直径。

证明：如图2，连接BD

BC，CD分别切⊙O于B，D

∴CD=CB，OC⊥DB又∵OC//AD，∴∠ADB=90°

∴AB是⊙O的直径

变换二：已知AB是⊙O的直径，OC平行于弦AD，CD切⊙O于D，求证：BC是⊙O的切线。

证明：如图3，连接OD

∵OC//AD，∴∠1=∠3，∠2=∠4

由∠1=∠2，∴∠3=∠4

又OD=OB，OC是公共边，

∴△COD≌△COB，∴∠B=∠ODC

∵CD切⊙O于D，∴∠ODC=90°，∴∠B=90°∴BC是⊙O的切线

……

此题将题目中的某些条件和结论互换以后得到一些新题。

总之，在教学实践中，教师应充分挖掘教材，提炼其中所蕴含的火花，并归纳总结上升到思想方法的高度，抓住实质，揭示规律，从更高层次上发挥例题、习题的功能作用，提高学生分析问题、解决问题和探索创新的能力。

编辑 王团兰endprint