单片晶圆兆声清洗的仿真模型研究

朱亚安，段 瑜，宋立媛，孙琪艳，殷艳娥，杨炜平，万锐敏，季华夏



单片晶圆兆声清洗的仿真模型研究

朱亚安1,2，段 瑜1,2，宋立媛1,2，孙琪艳1,2，殷艳娥1，杨炜平1，万锐敏1,2，季华夏1

（1.云南北方奥雷德光电科技股份有限公司，云南 昆明 650223；2.昆明物理研究所，云南 昆明 650223）

通过研究单片晶圆兆声清洗过程中兆声头在晶圆表面的运动轨迹和能量积累过程，构建了单晶圆清洗的兆声能量分布和颗粒去除过程的数学模型。通过Mathematica 9.0对模型进行了运算和简化，经过离散化处理后，运用MATLAB对几种硅片转速和兆声臂转速的组合在硅片上的能量分布和颗粒分布进行了模拟仿真。发现简单组合比例下清洗效果与转速比例和清洗轨迹复杂程度密切相关，而固定半径扫描可以使能量分布更均匀，减少局部能量集中对晶圆IC的破坏，并且可以缩短清洗时间。

单片晶圆；兆声清洗；仿真模型

0 引言

兆声清洗作为各种尺寸晶圆去除表面附着颗粒的基本手段已被广泛应用于IC制造工艺中，而随着IC集成度的提高和线宽的缩小，CMP工艺后对亚微米颗粒清洗的要求也越来越高。单片式晶圆清洗可以降低大直径晶圆批处理中的交叉污染和成品率损失的风险，并且可以满足晶圆背面、斜面和边缘清洗等多品种、小批量产品的要求，因此单晶圆兆声清洗技术得到了日益广泛的应用和发展。国外单晶圆设备制造商如SSEC、SEZ、FSI、SONOSYS、PROSYS等都拥有对单晶圆兆声清洗的专利技术和相关设备[1]，而国内对于单晶圆清洗工艺和设备才处于起步阶段，目前应用于产业化的国产晶圆清洗设备多以槽式批量晶圆清洗设备为主。

对于单片兆声清洗来说能量分布的不均匀会导致过剩能量破坏IC电路[2]，而随着柔性基底、玻璃基底以及多晶硅和透明氧化物TFT等技术的出现，由于其较低的工艺温度和非晶态物质本身较低的分子间作用力，使器件电路对基底的附着力和分子间结合的强度远低于传统单晶硅高温工艺。在一些特殊领域如MEMS和有微桥结构的非制冷红外焦平面阵列[3-5]制备工艺中刻蚀后的清洗也是决定成品率的关键因素，而这些工艺的特殊结构使得兆声能量分布的不均匀性对器件造成的损伤越来越明显。因此，对于单晶圆兆声清洗来说，兆声能量分布的研究以及颗粒去除模型的建立对于晶圆清洗工艺和清洗设备制造都有很大的指导意义。

1 兆声清洗原理

传统的超声波清洗技术是由换能器将28Hz以上的电能转换成高频机械震荡波[6]，通过去离子水或其他清洗剂将超声波能量传递到硅片表面。超声波传递的过程中伴随着机械波的辐射，并且不断的产生大量的微小气泡。由于空化作用，这些气泡在超声波作用下闭合的瞬时产生高压，不断地轰击硅片表面，使得附着在表面的颗粒迅速剥落。而兆声波清洗技术的原理是在清洗时由换能器发出频率为0.8MHz，波长为1.5mm的高能声波，产生高能（850kHz）频振效应结合化学清洗剂的化学反应对晶圆片进行清洗。液体分子在这种声波的挤压和推动下做加速运动，其最大瞬时速度可达30cm/s，兆声清洗对0.3mm以下的小颗粒有着较好的清洗效果。虽然目前有很多设备已经把原有的锥形水流喷嘴改进成了中央带小孔的圆饼形喷嘴，以图增大兆声作用面积，但兆声依然只是在水介质的带动下从中央小孔输出，加之随着频率的升高声波能量的衰减也逐渐增大[7]，兆声作用面积逐渐缩小，使得能量均匀化的效果并没有预想的结果好。

一般的单晶圆兆声清洗设备都由带有兆声喷头的机械摆臂和晶圆旋转托架组成，在晶圆旋转的同时，摆臂带着兆声喷头在晶圆表面做扫描运动，达到单晶圆清洗的效果。如图1所示。

图1 单晶圆兆声清洗示意图

2 单片晶圆兆声能量分布模型

2.1 兆声喷头和硅片的相对运动分析

在匀速运动下，摆臂的转角与时间的关系为一个三角波函数，由于三角波函数的一阶导数不连续性拟合时间只能在1/2个周期内，无法体现长时间的能量积累和轨迹变化情况，因此将其用傅里叶级数展开得到式(1)：

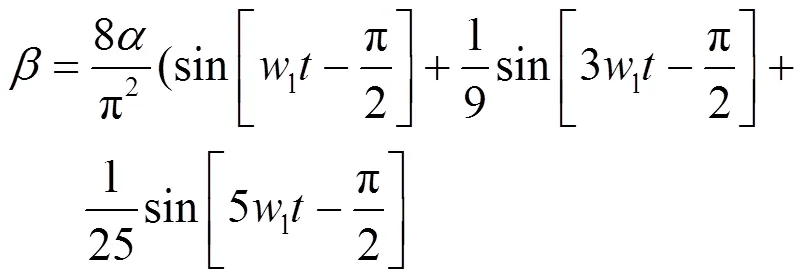
式中：a为摆臂的最大摆角；ww为硅片转速；wl为摆臂转速；r为硅片半径；l为摆臂长度。如图2所示。

图2中：为时刻硅片转角；为摆臂与圆心连线夹角；为兆声臂与轴夹角。各角度关系如下：

＝－(2)

＝w(3)

兆声臂在硅片上的速度分量如下，其中l为时刻摆臂中心点坐标处摆臂运动方向与轴夹角；w为时刻摆臂中心点坐标处的硅片运动方向与轴夹角；为合速度方向与轴夹角：

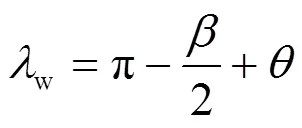
在硅片匀速转动和兆声摆臂做匀速往返运动时，摆臂端头的兆声喷头中心点在硅片表面经过的路径可以用如下参数方程表示：

2.2 兆声能量分布和模型的离散化处理

将携带兆声波的液膜近似看作均匀无限大介质，将衰减系数设为0.8[3]，则在距离兆声头中心处的兆声功率p如式(8)，其中m为兆声头中心处的输出功率，设为10W：

将上述参数式(1)～(7)带入式(8)中得到兆声功率分布函数，经过Mathematica计算简化后，得到硅片上时刻在(,)处的兆声功率如下式：

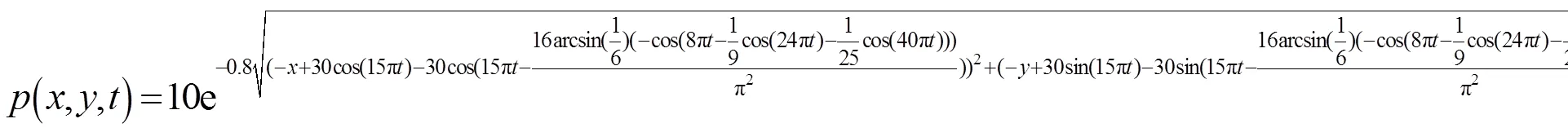
则时刻硅片上的总能量为：

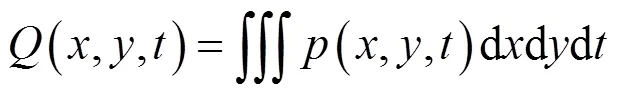
时刻硅片上的能量分布为：

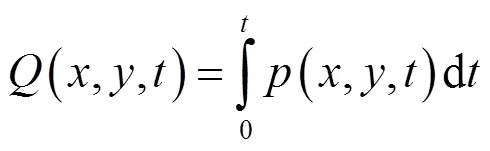
由于式(10)和式(11)都无法得出解析解，因此需要对其做离散化处理后转化为多个矩阵的和再由MATLAB运算。首先假设一个方形硅片，将硅片上能量覆盖的区域描述为一个201×201的矩阵，每一个阵元表示该坐标下的能量。再将时间坐标每1/10s为一个格点建立三维坐标系，若工艺时间为300s，则将生成一个201×201×3000的三维矩阵。结合式(7)的兆声头运动路径和式(9)的功率分布，则时刻硅片上坐标为(,)处所受到的兆声能量为：

由于在时段内，兆声能量不间断地作用于硅片表面，因此假设表面附着的颗粒只需要获得足够的兆声能量便可以实现脱附。

2.3 仿真结果与实验分析

将式(11)的能量积累分布函数作用于颗粒模型之上，得出每个颗粒所吸收的能量。由于颗粒的粒径很小，重力对其影响甚小可以忽略，类似于二维空间流体中的粒子运动，可见兆声能量在液体中传播时被颗粒吸收的几率函数基本符合玻尔兹曼分布。因此利用玻尔兹曼函数对颗粒吸收能量分布函数进行修饰后，得到式(12)：

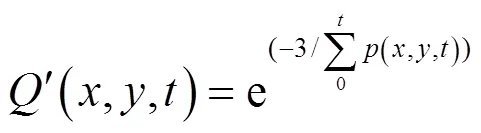
根据实验条件，对模型的边界进行限定后，用MATLAB对式(12)进行仿真，并对兆声头在硅片上的运行轨迹进行了综合对比。结合实际经验发现，硅片的清洗效果与兆声头在硅片上留下的清洗轨迹有很大关系，因此，我们以较为常见的8英寸（200mm）硅片为例，选择了4组不同的转速比例的工艺（(a)～(d)），和一组固定扫描半径工艺(e)进行了仿真，如表1所示。

表1 不同样品的转速比例

同时，利用MATLAB的RAND函数建立一个包含约2000个颗粒的随机分布模型，并且设颗粒的吸附能分布为正态分布，如图3所示。

图3 初始颗粒分布

经过300s后，兆声头的运动轨迹、晶圆表面累积的能量分布和清洗后剩余的颗粒分布见图4（(a)～(e)）、图5((a)～(e))所示。

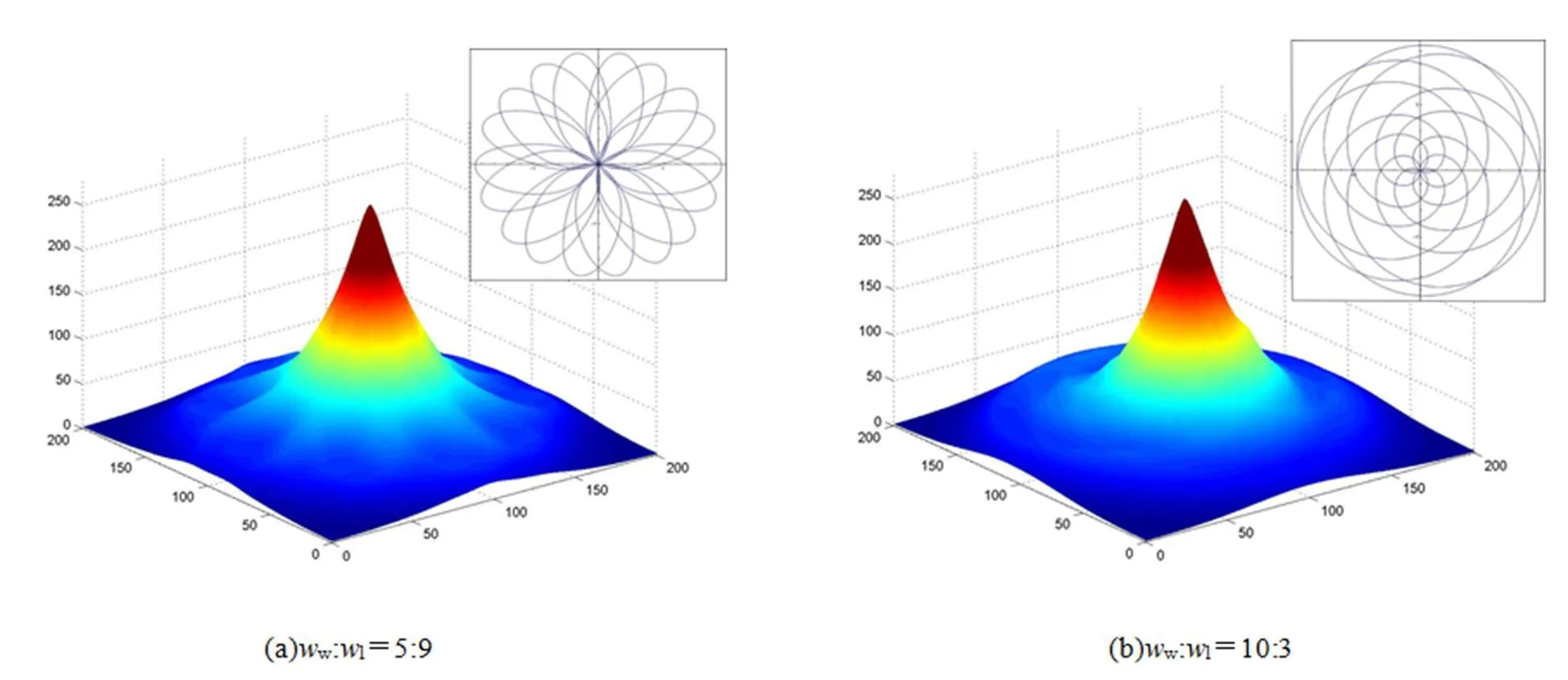
（固定半径1/4，2/4，3/4）

图4 不同转速比例下的兆声头运动轨迹和能量分布

Fig.4 Distribution of energy and trajectory of megasonic arm at different rotation speed ratios

（固定半径1/4，2/4，3/4）

图5 不同转速比例下的兆声头运动轨迹和能量分布

Fig.5 Distribution of energy and trajectory of megasonic arm at different rotation speed ratio

工艺时间在300s以内的不同转速比例下硅片上剩余颗粒百分比随工艺时间的变化趋势如图6所示。

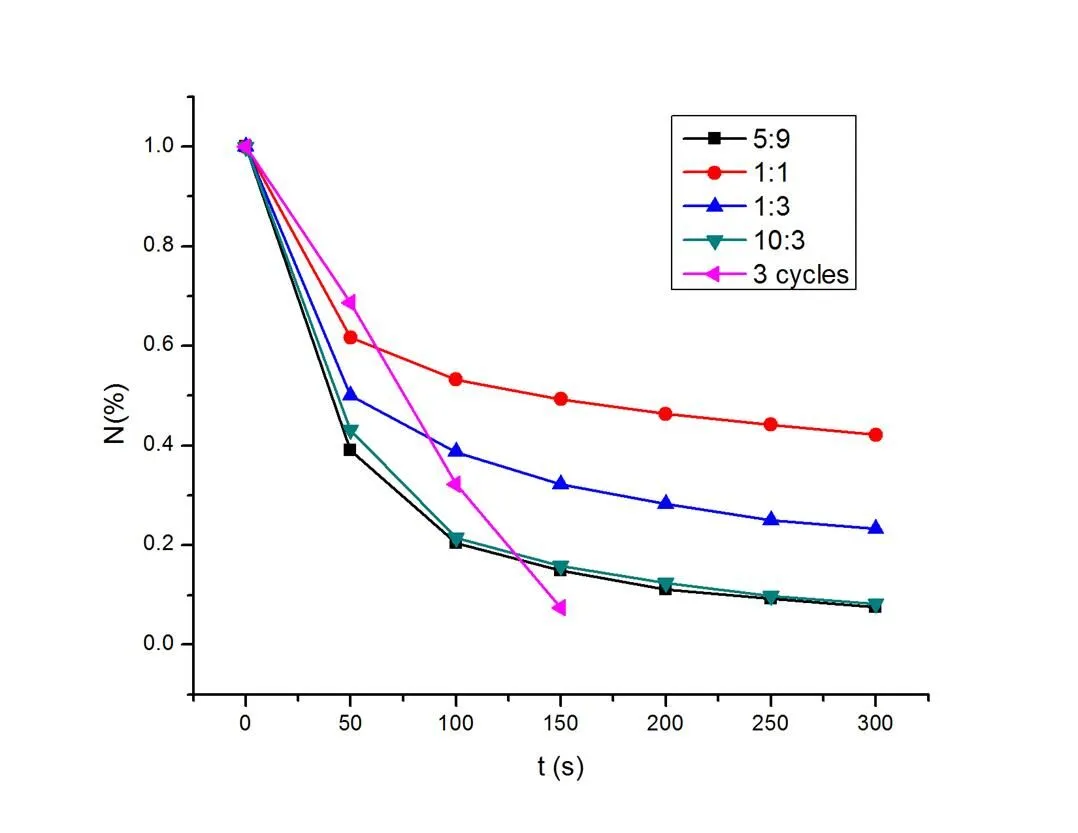
图6 不同转速比例下颗粒数随时间的变化

3 结果和讨论

本文对单晶圆兆声清洗的清洗硅基和能量分布进行了数值分析和建模计算，给出了计算方法，并对不同的清洗方法进行了仿真对比，从仿真结果可以得出如下结论：

1）兆声头运行轨迹和能量分布有着密切的关系，合理的转速比例关系可以使能量的覆盖更加全面，清洗更加彻底。应避免晶圆转速与兆声臂转速之间的简单比例的出现，应在合理的范围内尽量选取公倍数较大的比例关系。

2）从(a)和(b)的结果可以看出，在匀速清洗工艺下，当清洗路径基本覆盖硅片后，调整转速比例对减少颗粒已几乎没有贡献，应考虑使用固定半径扫描法节约工艺时间。

3）由于匀速旋转清洗（(a)～(d)）会多次经过中心，则必然出现晶圆中心位置能量聚集的现象，而固定半径分段扫描(e)可以将能量更加均匀的分布在晶圆上，避免能量集中造成的破坏。

4）固定半径分段扫描(e)虽然在前期清洗速率较慢，但是在后期清除90%以上颗粒花费的时间比匀速旋转清洗（(a) ～(d)）快，这是因为后者可以在短时间内将能量聚集在晶圆中心，而快速清除中心部分的颗粒，但是在周边的能量积累速度较慢，以至于出现了清洗不均匀的现象。

[1] 刘永进, 杜建科, 冯小强. 单晶圆兆声清洗技术研究及兆声喷头方案优化[J]. 电子工业专用设备, 2011, 40(001): 15-17.

[2] Mertens P. Damage-free removal of nano-sized particles, heading towards a red brick wall[C]//. 2003.

[3] 许娅明, 任华. 320× 240混合式非制冷红外焦平面探测器芯片工艺研究[J]. 红外技术, 2011, 32(1): 1-5.

[4] 袁俊, 太云见, 雷晓虹, 等. 氧化钒非制冷红外焦平面探测器芯片工艺研究[J]. 红外技术, 2009, 31(1): 1-4.

[5] 赵利俊, 欧文, 闫建华, 等. 一种与 CMOS 工艺兼容的热电堆红外探测器[J]. 红外技术, 2012, 34(2): 89-94.

[6] 马大酞, 沈壕. 声学手册[M]. 北京: 科学出版社, 2004.

[7] 刘伯胜, 雷家熠. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 1998.

Study on Simulation Model of Single-wafer Megasonic Cleaning

ZHU Ya-an1,2，DUAN Yu1,2，SONG Li-yuan1,2，SUN Qi-yan1,2，YIN Yan-e1，YANG Wei-ping1，WAN Rui-min1,2，JI Hua-xia1

(1.650223,; 2.650223,)

A mode for calculating the distribution of megasonic energy and the process of particles cleaning is demonstrated by studying the distribution of megasonic energy and motion trail of megasonic arm in the single wafer. The model is simplified by Mathematica 9.0 and simulated by MATLAB under different rotation speed ratios, which indicates that the cleaning effect is closely related to the rotation speed and the motion trail of megasonic arm. Meantime，the distribution of megasonic energy becomes more uniformity by fixing the scanning radius, which also could reduce the damage to IC and the process time.

single-wafer，megasonic cleaning，simulation model

TH132

A

1001-8891(2015)01-0048-06

2014-05-15；

2014-10-28.

朱亚安（1983-），男，工程师，主要从事晶圆清洗和OLED器件制造工艺。

云南省应用基础研究重点项目，编号：2012FA004。