静态红外地平仪大角度测量模型及误差研究

李 鑫，崔文楠，周士兵



静态红外地平仪大角度测量模型及误差研究

李 鑫，崔文楠，周士兵

（中国科学院上海技术物理研究所，上海 200083）

卫星姿态变化时，静态红外地平仪的成像面与地平圆之间的夹角也会随着变化，因此会造成地平圆在地平仪成像面上成像的变化，进而导致地平仪大角度测量误差增大。为解决此问题，建立了随卫星姿态变化时地平圆在静态外红地平仪成像面上的成像模型，通过STK仿真对该模型进行验证，并给出了一种基于该模型的地平仪测量误差校正的方法，为卫星姿态测量与控制提供补偿和精度保证。

测量模型；大角度测量；误差分析；静态红外地平仪

0 引言

近年来人们对卫星姿态控制精度的要求不断提高，同时卫星向着小型化发展。红外地平仪作为卫星姿态控制系统的关键部件之一，如何提高其测角精度，减小其体积是目前红外地平仪研究的热点之一[1-2]。与扫描式红外地平仪相比，静态红外地平仪具有无扫描机构、重量轻、精度高、功耗低、使用寿命较长的特点[3]，因此各国都在积极对此进行研究[4-5]。

近年来，人们主要针对地球扁率对红外地平仪的测角误差进行研究[6-8]，而很少对因卫星姿态变化导致地平圆在静态红外地平仪成像面上成像非圆成像引起的测量误差进行研究。本文推导出静态地平仪姿态计算的数学模型，同时建立了随卫星姿态变化，地平圆在静态红外地平仪成像面上非圆成像的模型，通过STK仿真对该模型进行验证，最后给出一种基于该模型的大角度测量误差校正的方法。

1 静态地平仪测角模型

地球的扁率约为0.003[6]，可以近似认为是一个标准的圆球体。静态红外地平仪采用凝视技术，从太空观测地球时，得到相当于在4K冷背景中的一个平均亮温约为220～240K的圆盘，圆盘的边缘称为地平圆，如图1所示¢为地平圆的圆心，¢为局地垂线。

地平仪是通过探测器检测地平圆上的地球红外辐射能量，确定对应点的方位角位置，得到卫星相对于地球局地垂线的俯仰角和滚动角，从而确定卫星姿态。因此基于地平仪的卫星姿态测量应该在卫星坐标系(,,)下进行。如图1所示，从卫星坐标系观察地平圆的示意图。

根据图1，推导出卫星俯仰角、滚动角与卫星方位角和静态地平仪半张角的关系如式(1)[7]：

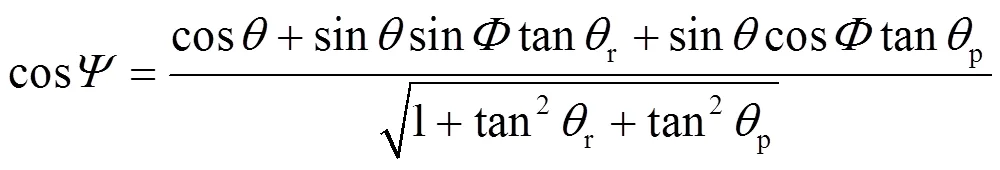
式中：qr，qp分别为卫星的滚动角和俯仰角；q为穿越点与Y轴也即卫星俯仰角与滚动角都为0时局地垂线的夹角；Y为地平仪的半张角；F为卫星方位角。理论上只要找到3个地平点，然后计算出3个地平点的q角，就可以根据公式(1)，计算出卫星的滚动角qr和俯仰角qp。

如图2所示，假设在方位角为0、p/2、p、3p/2上有4个地平点，4个地平点对应的角为1、2、3、4[9-10]。分别代入式(1)，可得式(2)，式(3)[6]：

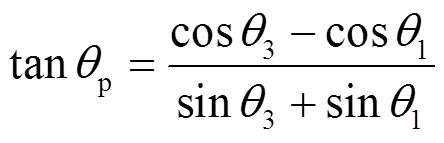
实际计算中，需要获取地平圆在静态地平仪成像面上的穿越点来计算1、2、3、4。如图3所示，在地平仪成像面上我们可以获取穿越点、的像素值，进而求出此像素值距离¢的距离1和3。

对于静态红外地平仪，远远大于¢，可以近似认为¢＝，为镜头焦距。所以cos1、sin1、cos3、sin3如式(4)～(7)：

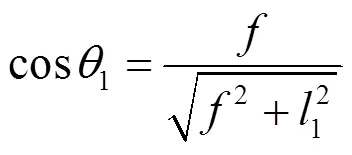
图3 红外地平仪探测到地平圆

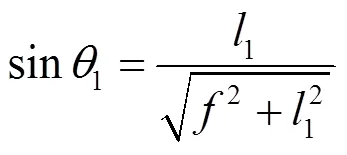
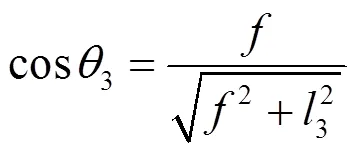
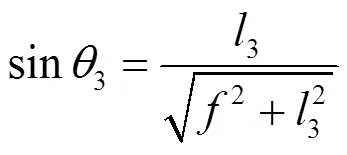
将式(4)～(7)代入式(2)，可得p如式(8)：

同理可得r如式(9)：

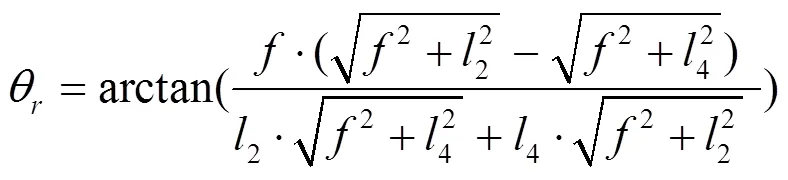
2 静态红外地平成像模型

当卫星姿态发生变化时，静态红外地平仪的成像面也会随着发生变化，当卫星姿态变化r、p时，静态红外地平仪的成像面将不再与地平圆所在平面平行，如图4所示。

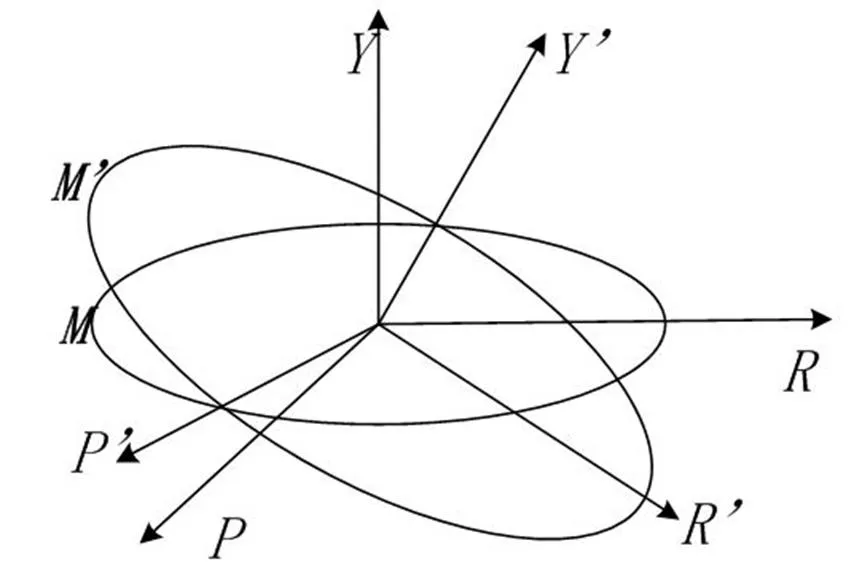
图4 卫星姿态偏转时地平圆变化

在图4中，平面为卫星滚动角和俯仰角为0时，静态地平仪的成像面与地平圆平行；平面¢为卫星姿态变化r、p时静态地平仪的成像面。对于平面上的任一点(,,)，通过坐标变换得到(¢,¢,¢)如式(10)：

(¢,¢,¢)＝r(r)×p(p)×(,,) (10)

式中：p(p)，r(r)如式(11)、(12)：

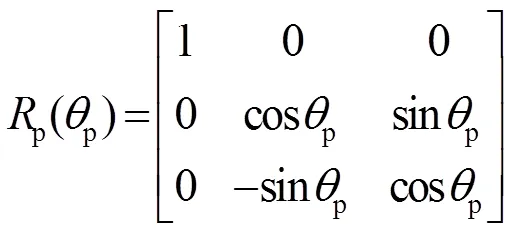
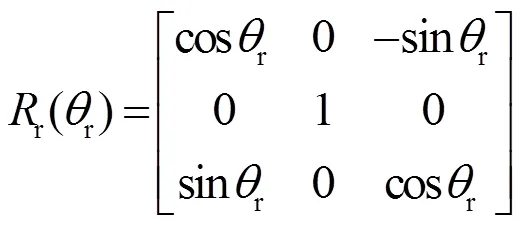
当卫星俯仰角及滚动角为r、p时，假设在成像面上地平圆半径为，圆心为(,, 0)，地平圆方程如式(13)：

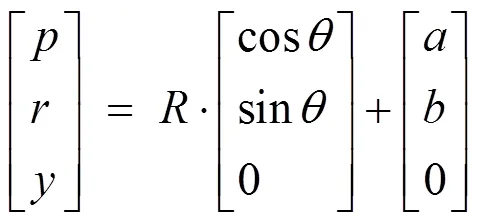
将(13)式代入(10)式可以求出坐标变换系(¢,¢,¢)下的表达式如式(14)所示：

式中：TM、PM如式(15)、(16)：

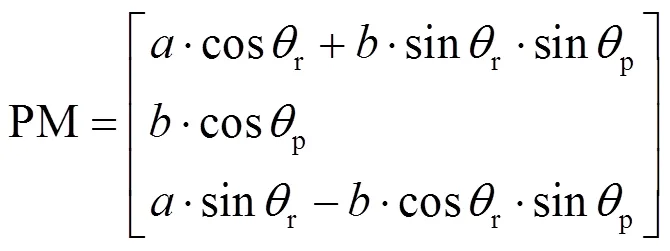
所以地平圆沿光轴也即¢在平面¢上的投影方程如式(17)～式(19)所示：

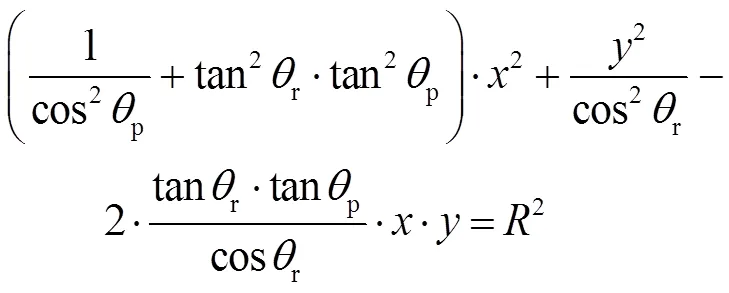
＝¢－×cosr－×sinr×sinp(18)

＝¢－×cosp(19)

由式(17)～式(19)可以看出，当卫星姿态发生变化时，地平圆在地平仪成像面上变成了椭圆。

如图5所示，当卫星绕着滚动轴旋转一个角度时，若焦平面仍然平行于地平圆，则地平圆成像为图5中虚线所示的圆，穿越点为、、、；但是实际上，由于成像面随着卫星姿态的偏转，成像面与地平圆面不平行，在新的成像面上成像为图5实线所示的椭圆。而穿越点在线阵上的位置为¢、¢、¢、¢。若将¢、¢、¢、¢作为穿越点代入式(8)计算卫星的滚动角，必然会引起误差。

当卫星姿态发生变化时，可以根据上述模型求出穿越点、、、和¢、¢、¢、¢具体的位置关系，进而对卫星姿态测量与控制进行补偿。

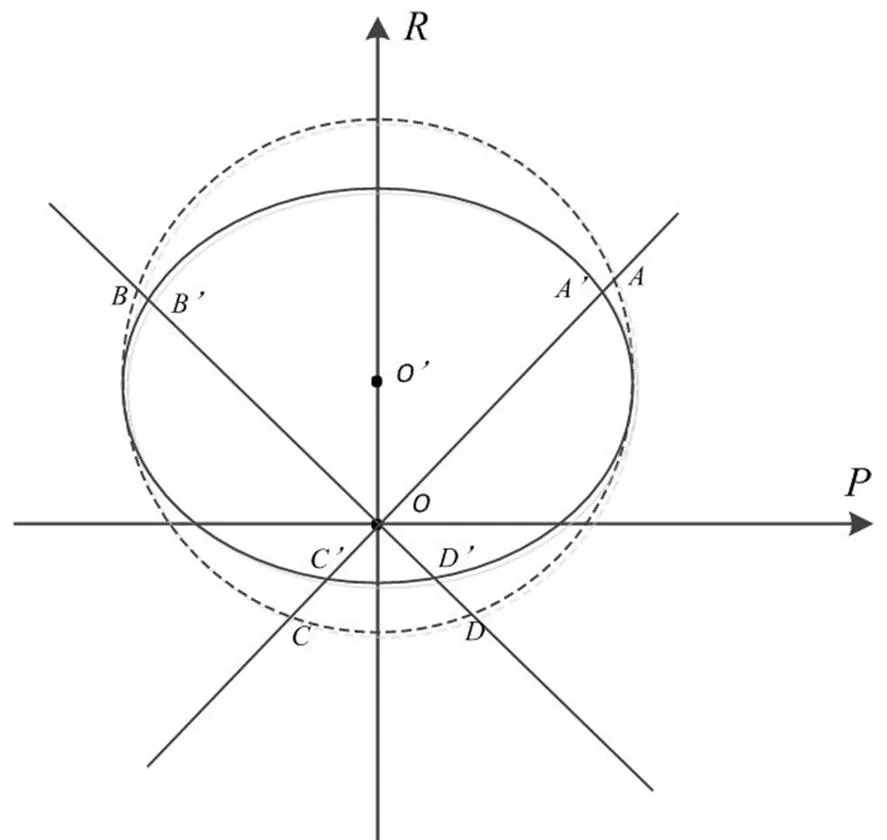
图5 卫星绕俯仰轴旋转时成像面成像

3 仿真分析

如图6所示，利用STK软件对一种线阵静态红外地平仪进行仿真[11]。轨道参数为：轨道高度700km，倾角为97°，降交点地方时为12:00，地平仪参数为：每个线阵大小为1×640，视场为0.1°×64°，每个线阵光轴与偏航轴夹角为65°的。

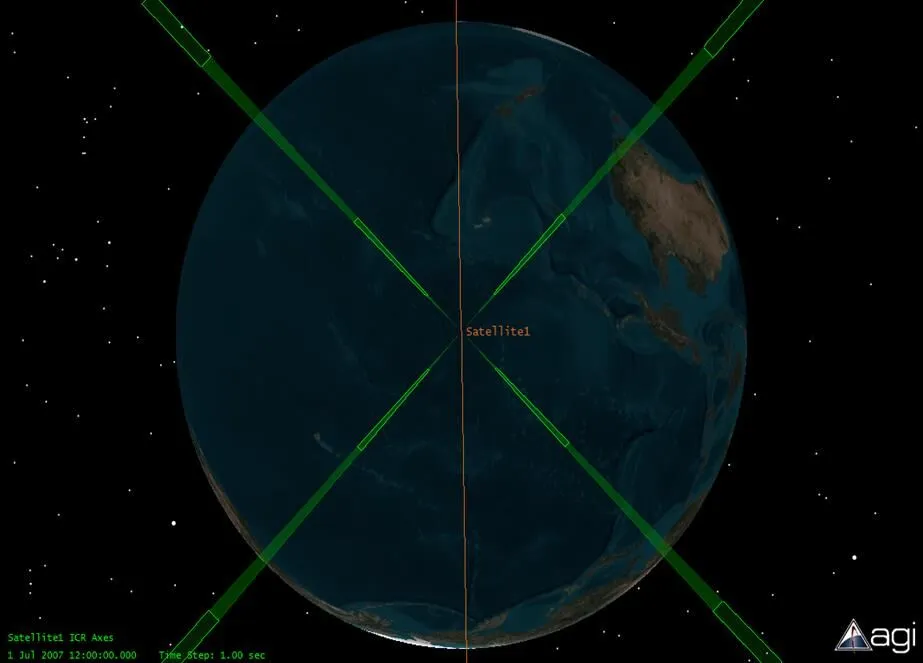
图6 STK仿真模型

如图7所示，其中‘*’所示数据为根据式(15)以及图5所示椭圆模型得到穿越点在线阵探测器位置，‘+’所示数据为STK中卫星绕滚动轴从0°～32°转动时，穿越点在线阵探测器的位置。

图7 滚动轴偏转时第一象限穿越点像素值

图8为当卫星绕俯仰角转动时，穿越点在第一象限变化情况，其中‘*’为根据式(15)模型计算得到穿越点位置，‘+’为STK仿真数据穿越点的位置。

从图7和图8可以看出，上述模型计算结果与STK仿真结果基本一致。

在滚动轴和俯仰轴偏转时，利用数学模型求出、、、，利用STK仿真¢、¢、¢、¢，代入式(8)进行计算，滚动角和俯仰角计算误差曲线分别如图8和图9所示。

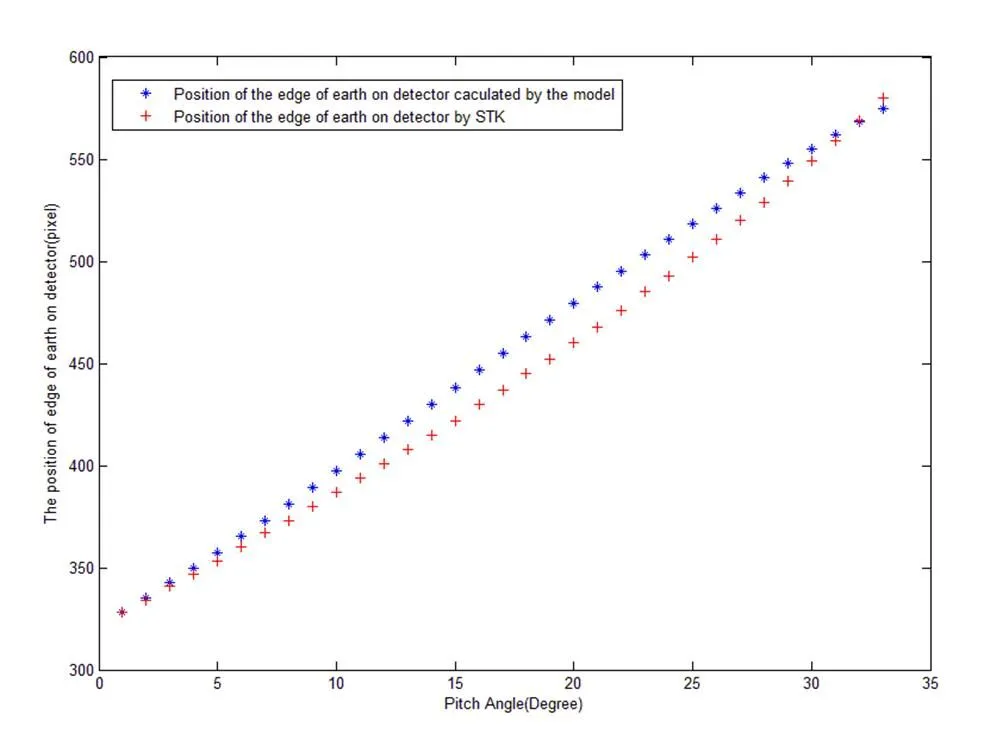
图8 俯仰轴偏转时第一象限穿越点像素值

Fig8 The horizon edge on detector with the change of pitch angle at first quadrant

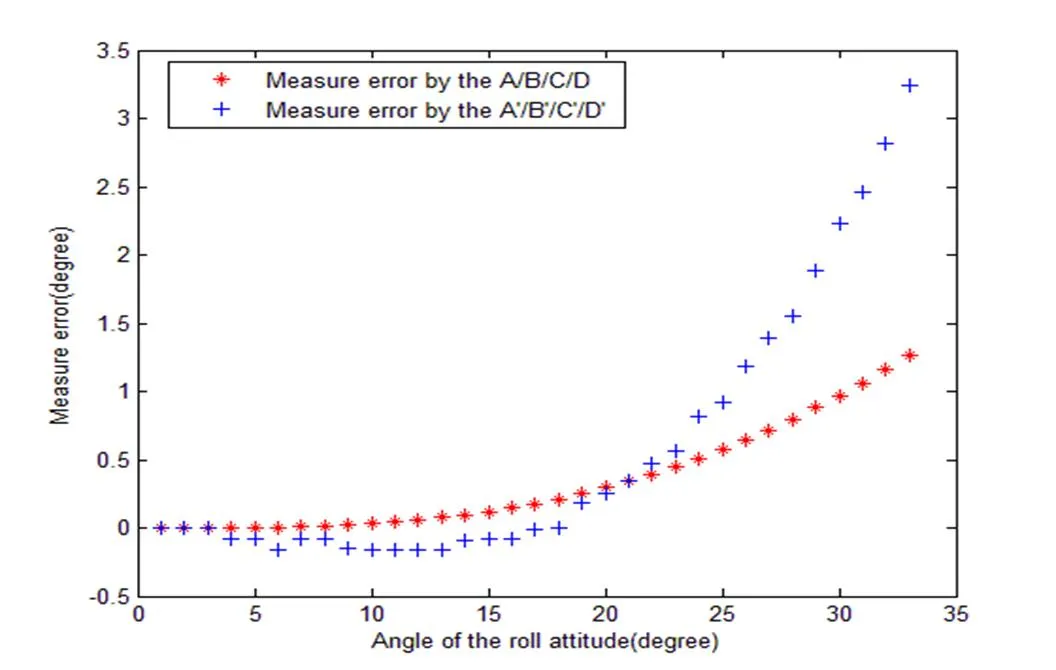
图9 滚动角测量误差

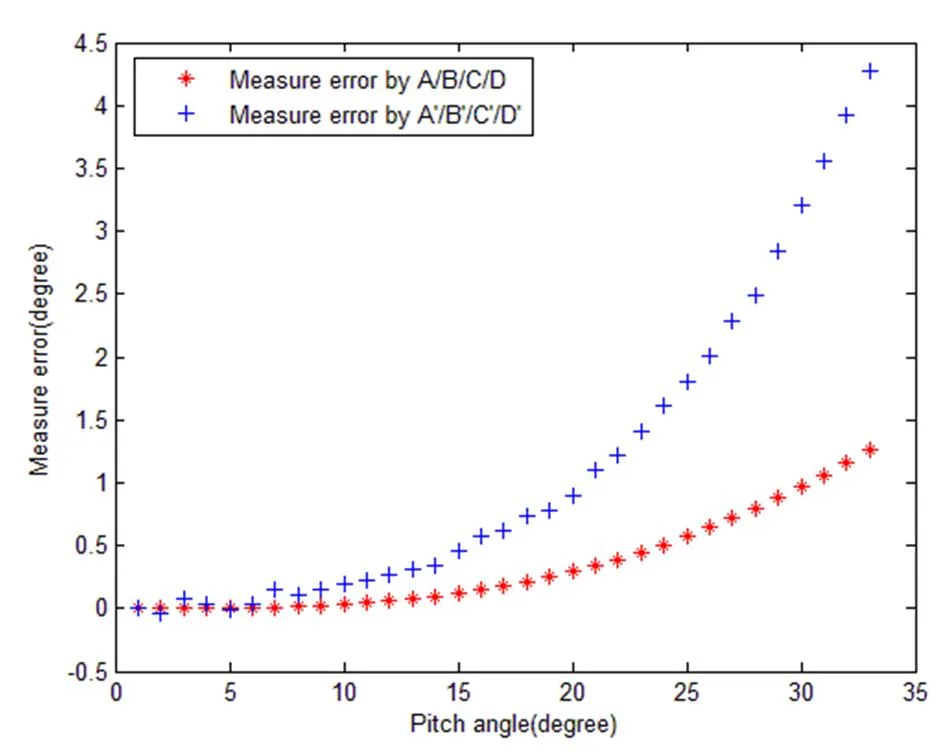
图10 俯仰角测量误差

由图9可见，根据A、B、C、D为穿越点求出的滚动角在0～20°最大误差为0.3402°，利用¢、¢、¢、¢求出的滚动角最大误差为0.3391°，在20°以内两种方法计算误差基本一致，但是、、、为穿越点求得滚动误差线性度较好。在21°～32°时，根据、、、为穿越点求出的滚动角最大误差为1.26°，而利用¢、¢、¢、¢求出的滚动角最大误差为3.236°。由图10可以看出，以¢、¢、¢、¢为穿越点计算俯仰角误差最大为4.276°，而以、、、计算俯仰角最大误差为1.261°。将、、、作为穿越点计算误差明显小于利用¢、¢、¢、¢求出的滚动角误差。

在实际应用中，可以根据数学模型求出不同卫星姿态时、、、与¢、¢、¢、¢关系，然后对其关系曲线进行拟合，从而可以由测量到的¢、¢、¢、¢对、、、进行补偿，然后进行卫星姿态计算，从而提高较大角度时地平仪的测量精度。

4 结论

本文给出了地平圆在卫星姿态变化时在成像面上的成像模型，并利用STK软件对该模型进行验证。实验结果可以发现，该模型与STK仿真结果一致性较好，且利用该模型对卫星姿态测量进行补偿时，在大角度时测量结果误差明显减小。该模型的推导研究对大视场、高精度地平仪测量精度的提高具有重要意义。

[1] 郭振东. 应用于微小卫星的地球敏感器设计与优化[D]. 杭州: 浙江大学, 2013.

[2] Si Mohammed A M, Benyettou M, Bentoutou Y. Three-axis active control system for gravity gradient stabilized microsatellite[J]., 2009, 64: 796-809.

[3] Geoffray H, Bardoux A, Laporte M. Uncooled infrared microbolometers arrays for earth remote sensing[C]//, 2000, 4130: 527-537.

[4]: 何丽, 胡以华. 红外地球敏感器的技术发展趋势[J]. 传感器与微系统, 2006, 25(7): 4-6.

[5] 周士兵, 杨晓宇. 基于电机转速的红外地平仪测量误差研究[J]. 红外技术, 2009, 31(10): 598-601.

[6] 姜雪源, 马广富, 罗晶. 红外地平仪姿态测量误差模型[J]. 宇航学报, 2003, 24(2): 138-143.

[7] 李宇衡, 易克初, 田红心. 一种提高红外地平仪确定卫星姿态精度的方法[J]. 红外与毫米波学报, 2007, 26(3): 178-181.

[8] 周军, 钱勇. 基于地球扁率红外地平仪测量值修正算法研究[J]. 宇航学报, 2003, 24(2): 144-149.

[9] 张华达. 红外面阵焦平面静态地平仪[J]. 红外, 2004(2): 1-9.

[10] 沈国权, 王昊, 郭振东. 面向微小卫星的红外静态焦平面地球敏感器设计[J]. 传感技术学报, 2012, 25(5): 571-576.

[11] 吕银环, 雷存栋, 张涛, 等. 线阵静态红外地平仪新型地球模拟器[J]. 红外与激光工程, 2012, 41(10): 2785-2790.

Wide Angle Attitude Measuring Model and Error Analysis of Static-infrared Earth Sensor

LI Xin，CUI Wen-nan，ZHOU Shi-bing

(200083,)

With the change of satellite attitude, the angle between the imaging plane of static-infrared earth sensor and horizon also changes. This will cause the image of horizon on the imaging plane is not a circle. So the measurement error occurs. To solve the problem, the horizon imaging model on the imaging plane of static-infrared earth sensor is built. The model is verified by STK simulation. At last, a way to correct the measuring error of static-infrared Earth Sensor is given based on this model.

attitude measuring model，wide attitude measurement，error analysis，static-infrared sensor

V448.2

A

1001-8891(2015)01-0073-05

2014-09-01；

2014-12-03.

李鑫（1990-），男，安徽蒙城人，研究生，主要从事卫星姿态测控、红外半物理仿真系统研究。E-mail：zjulixin@126.com。

装备预先研究项目，编号：61501020303。