基于傅里叶变换的森林红外图像增强算法研究
2015-03-30丁德红
崔 帅,刘 波,丁德红
基于傅里叶变换的森林红外图像增强算法研究
崔 帅,刘 波,丁德红
(湖南农业大学信息科学技术学院,湖南 长沙 410128)
以红外热监控技术在森林火警中的研究为背景,针对森林红外热图像低对比度、噪声大的特点,提出了用傅里叶变换理论对森林红外图像增强。分别用理想低通滤波器、巴特沃斯高通滤波器和同态滤波器对图像做了增强。结果对比后得出,同态滤波克服了低通滤波和高通滤波的缺点,图像细节和对比度得到明显增强。并进一步优化了同态滤波器中的指数型滤波函数,仿真结果表明,优化后的指数型滤波函数对森林红外图像有更好的增强效果,能提供更满意的图像。
图像增强;傅里叶变换;红外图像;滤波器
0 引言
红外热成像技术是森林火警措施中的一个重要技术,但是红外热传感器输出的信号常常存在着非均匀性以及噪声大、噪声种类多,所以可能会造成红外信号的目标难以识别,特别是在森林红外图像,整体灰度区分度不大,图像相对模糊,所以从中获得有用的信息需要对图像进行一定的加强处理。传统的图像增强方法[1]基本上是在图像空域内的研究,如灰度增强、直方图增强、空域滤波等。
近年来基于傅里叶变换理论,对图像进行频域内处理算法有很大发展。文献[2]提出首先用自适应中值滤波对红外图像进行去噪,保证噪声不被增强,然后利用同态滤波对图像细节进行增强,最后联合使用限制对比度自适应直方图均衡进一步调整图像的动态范围。文献[3]提出了一种单尺度双边滤波的图像增强算法,首先对采集图像亮度增强,然后利用双边滤波消除光照对图像不利影响,最后采用单尺度Retinex算法[4]对图像进行增强。文献[5]提出了一种图像空域跟频域相结合的方法来处理红外图像细节。本文将重点研究在傅里叶变换理论下,将图像由空域变换到频域,进行频域滤波处理,最后再利用傅里叶反变换理论将图像变换到空域。在MATLAB环境下,分别利用3种滤波函数对图像进行增强,并利用图像处理后的直方图对这3种滤波进行灰度分量[6]上的对比和总结。
1 基于傅里叶变换的图像增强算法
频域增强的流程是先对图像进行傅里叶变换;然后对变换后的图像进行滤波处理[7-8],变换后的图像实际上是矩阵的图像表示,不是普通的图像;最后将处理后的图像再使用逆变换变回空域,得到普通意义上的图像;最后再对处理后的图像进行主观上和直方图上的质量对比。其算法流程图如图1所示。
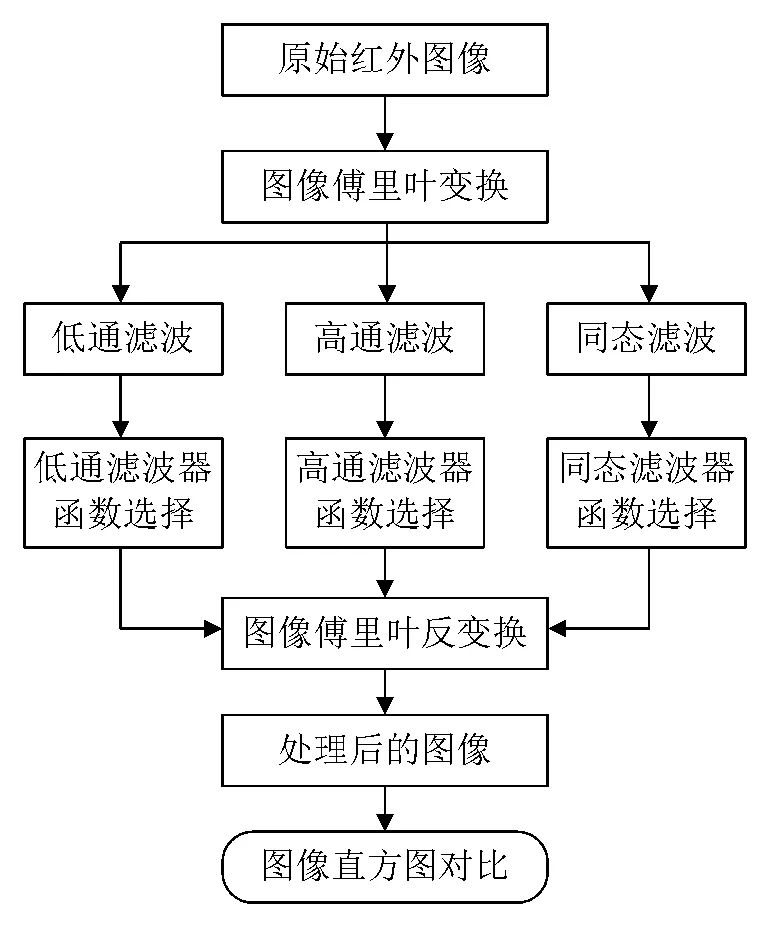
图1 算法流程图
1.1 傅里叶变换及反变换
在对图形进行频域内的处理时,首先要将图像从空域变换到频率域内。这一任务交给傅里叶变换来完成。在数字图像处理中,图像是二维的,一般要用到二维离散函数的傅里叶变换。在二维的情况下,傅里叶变换对表示为:
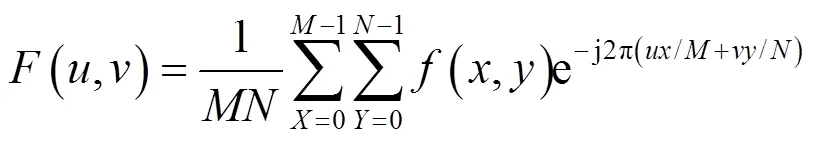
式中:=0, 1, 2, …,-1;=0, 1, 2, …,-1。(,)是函数(,)在×的空间上等间隔采样得到的二维离散信号,和是离散实变量,和为离散频率变量。
图像在频域内进行滤波处理后,要使图像从频域变换到空域,这一步就要用到傅里叶反变换理论。其傅里叶反变换公式为:
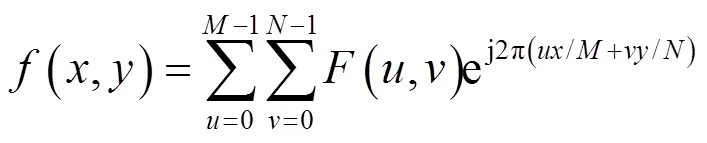
式中:=0, 1, 2, …,-1;=0, 1, 2, …,-1。离散傅里叶变换建立了函数在空间域与频率域之间的转换关系。
1.2 滤波器
滤波器的选择是频域内图像处理非常重要的一步,下面将分别对低通滤波器、高通滤波器和同态滤波器做较为详尽的研究。
1.2.1 理想低通滤波器
图像经过二维傅里叶变换后,噪声频率一般位于空间频率较高区域,而图像本身的频率分量处于空间频率较低的区域内。因此,可以通过低通滤波的方法使高频分量受到抑制,而让低频成分通过,实现图像的平滑:
(,)=(,)(,)
式中:(,)是原始图像的傅里叶频谱;(,)是平滑后图像的傅里叶频谱;(,)是滤波器的传递函数(频谱响应)。
理想二维传递函数为:
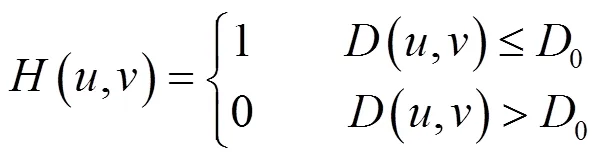
式中:(,)=(2+2)1/2,0是截止频率。理想低通滤波器(ILPF)是指在半径为0的圆内,所有频率没有衰减的通过滤波器,在此半径之外的所有频率完全被衰减掉。
1.2.2 巴特沃斯高通滤波器
高通滤波是对前面低通滤波的反操作,以得到图像中的高频成分,这个过程是图像锐化的过程。其目的是突出图像的边缘信息,加强图像的轮廓特征。
阶具有0截止频率的巴特沃斯高通滤波器的传递函数为:
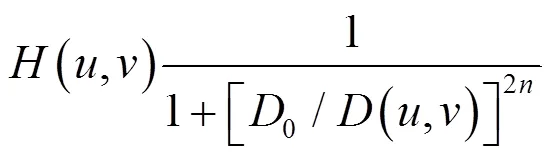
=1时,一阶巴特沃斯高通滤波器的传递函数为:
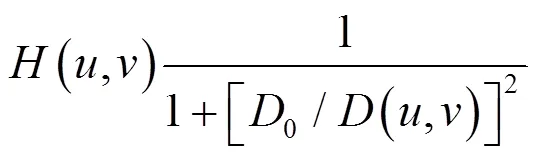
同低通滤波的情况一样,我们可以认为当巴特沃斯高通滤波器的阶数越高时越接近理想高通滤波器的处理效果。反之,当阶数=1时,图像相对要平滑一些。
1.2.3 指数型同态滤波器
同态滤波是一种在频率中同时将图像亮度范围进行压缩和将图像对比图进行增强的方法[9]。其作用是对图像灰度范围进行调整,通过消除图像上照明不均的问题,增强暗区的图像细节,同时又不损失亮区的图像细节。
一般自然景物的图像(,)可由照明函数(,)和反射函数(,)的乘积表示。(,)描述景物的照明,与景物无关;(,)包含景物的细节,与照明无关。其表达式:
(,)=(,)(,) (6)
由于两者相乘,无法变换到频域再分开处理,而对数函数能把乘积转变为相加,故对式(6)取对数,并命
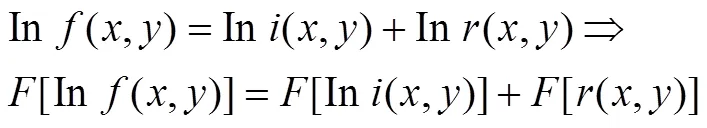
傅里叶变换得到:
(,)=(,)+(,) (7)
(,):照明函数在空间上变化缓慢,其频谱特性集中在低频段;
(,):反射函数的频谱集中在高频段(景物本身具有较多的细节和边缘),反射函数描述的景物,反映图像的细节内容,其频率处于高频区域。同态滤波流程图如图2所示。
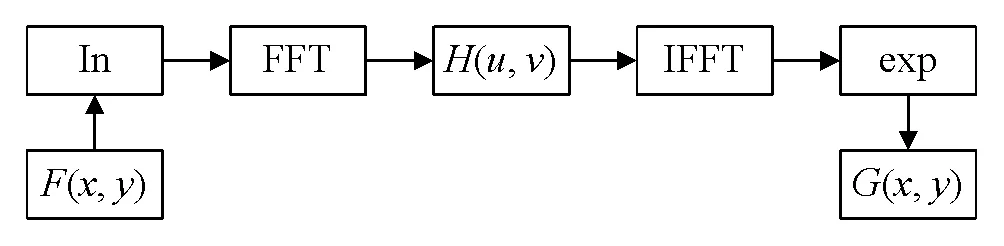
图2 同态滤波流程图
借助一个滤波函数(,)来处理(,),可以从公式(7)得到:
(,)(,)=(,)(,)+(,)(,) (8)
式中:(,)为同态滤波的函数,(,)函数表达式要选择高通滤波函数,这里我们选择指数型高通滤波函数其表达式:
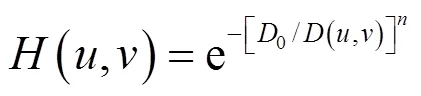
参数控制着传递函数的增长率。指数高通滤波器高低频率的过度比较光滑,而且用它处理过的图像没有明显的振铃现象。指数型高通滤波函数乘以高频增益后,得到如下公式:
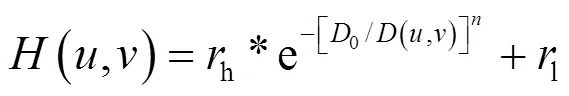
1.3 实验仿真
1.3.1 图像采集
为精准的研究频域内的森林红外图像算法,对森林红外图像这一特殊图像。我们对湖南长沙的岳麓山区,进行了图像采集。
硬件设备:双视频红外摄像仪1台,宏基笔记本1台,Intel Core i3-380双核处理器,4G DDR3内存,500G SATA2.0硬盘。
采集环境:白天;测试距离约1.6km;气温25℃左右。
1.3.2 基于MATLAB环境下的图像处理
下面将分别对理想低通滤波器、巴特沃斯高通滤波器和指数同态滤波器对采集到的图像进行处理。首先用MATLAB输出原图像的直方图,以便跟处理后的图像进行对比,如图3所示。首先设置理想低通滤波器中的截止频率0=80,然后利用MATLAB中的FFT2函数进行傅里叶变换,fftshift函数进行分量的平移得到处理后的图像及其直方图,如图4所示。
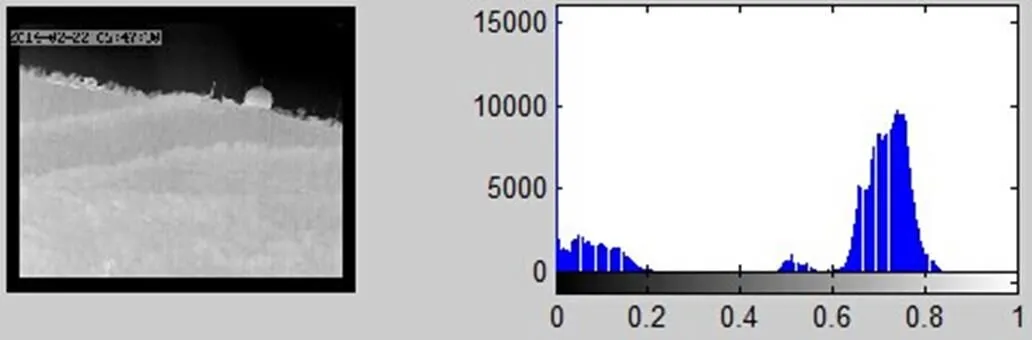
图3 原始图像及直方图
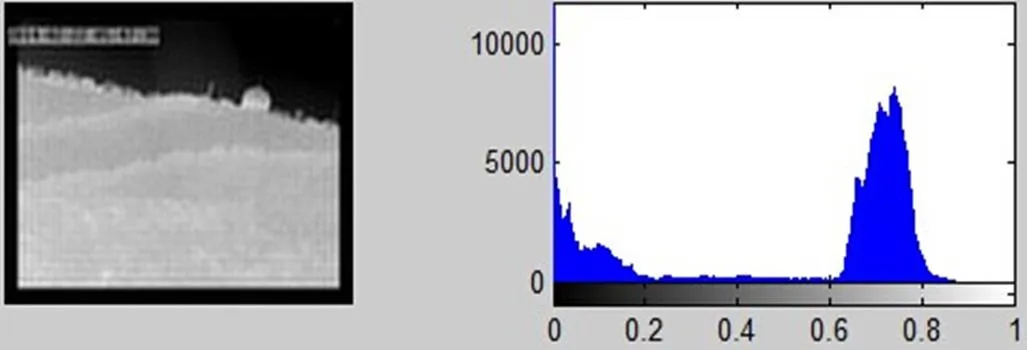
图4 理想低通滤波处理后图像及直方图
经过理想低通滤波器滤除频率在80Hz以上的高频部分后,从主观上来讲,图4中的图像相对于原始图像对比度强的地方趋于平滑,图像整体区域模糊。对比图3和图4中的直方图可以看出,两幅图处于0~0.2和0.6~0.8之间的灰度分量并没有太大变化,这是图像本身的原因,图像上半部分大体趋于黑色,灰度分量处于0~0.2之间;下半部分大体区域0.6~0.8之间;而原始直方图2.1~3处于0.4~0.6之间的小高峰,经过低频处理后均衡化,灰度分量比较均匀地分布到0.2~0.6之间。
接下来用巴特沃斯高通滤波器对图像进行处理,同样把截止频率0设置为80,阶数设置为1,得到图5。
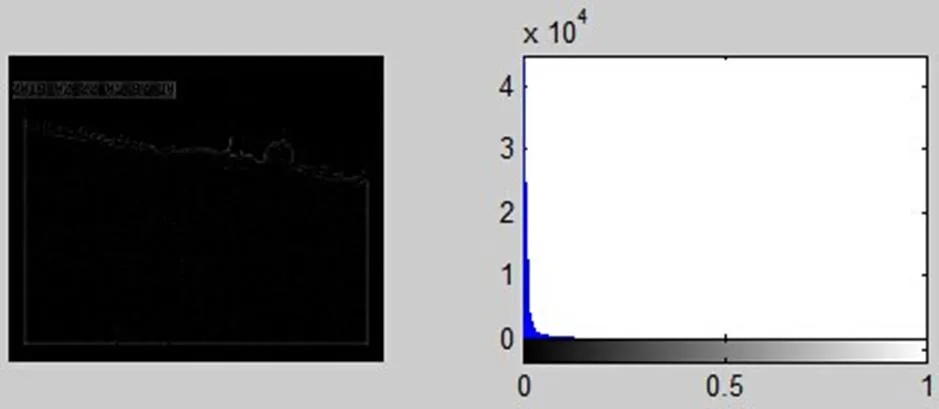
图5 巴特沃斯高通滤波处理后图像及直方图
可以非常明显地看出,经过把巴特沃斯高通滤波器之后,图5的锐化效果要比原始图像明显得多。2幅图中灰度变化大的部分被突出了,模糊了灰度变化小的部分。通过对比原始图像和经过巴特沃斯高通滤波器处理后的直方图,0.6~0.8之间的灰度分量几乎没有,滤除了80Hz以下的频率之后,图像整体黑暗,只有森林的轮廓可以大体看清。
最后用同态滤波器对图像进行增强,同态滤波器中的(,)我们选用指数型高通滤波函数,分别设置函数增长指数=2,截止频率0=80,高频增益值h=2和低频增益值l=0.5,得到处理后图像及直方图,如图6所示。
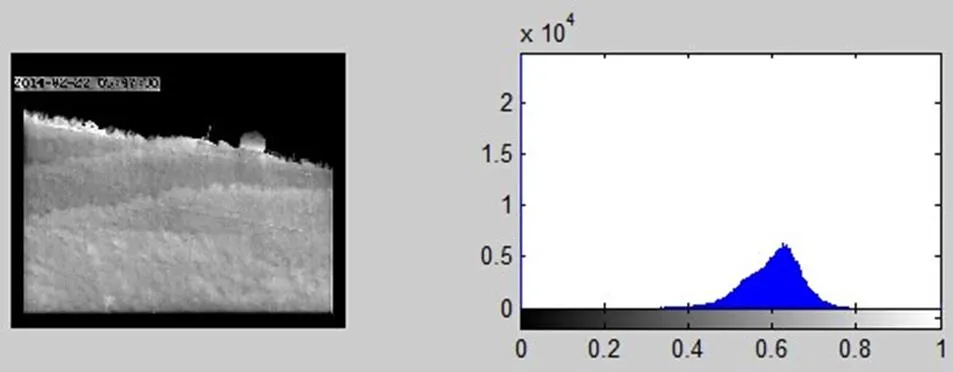
图6 同态滤波处理后图像及直方图
图6中很明显可以看出相对于原始的森林红外灰度图像对比度有所增加。亮区的细节没有大变化的情况下,图像暗区的细节得以增强。经过同态滤波器处理后,原始图像直方图的2个峰值变为1个峰值,原始图像中上半部分主要灰度集中在0~0.2之间和下半部分主要集中在0.6~0.8之间的灰度分量,由于增强了高频部分,对比度增加,灰度分量主要压缩到以0.6为峰值的0.4~0.8之间。
1.3.3 实验结果总结
通过对理想低通滤波、巴特沃斯高通滤波和同态滤波在频域内对森林红外图像的研究分析,可以看出低通滤波在滤除高频变化方面有明显的优势,巴特沃斯高通滤波增强了图像的高频分量。而此森林红外图像的灰度主要以低频部分为主,图像对比度不明显。同态滤波能很好地增强图像的对比度和细节,对处理森林红外图像有很好的作用。
2 指数型滤波函数优化
从上一章的仿真实验中我们得出同态滤波器对森林红外图像加强有非常好的效果,针对同态滤波器中的指数型高通滤波函数,本文对其做了进一步的优化,并且对优化后的指数型函数跟原始函数进行了对比。
首先,指数高通滤波函数变为指数低通滤波函数,因为低通滤波传递函数波形图跟高通滤波传递函数的波形图是相反的,所以用1减去低通滤波传递函数,同样,用高频增益量减去低频增益量。为锐化系数,可以进一步加强图像对比对。优化后得到如下公式:
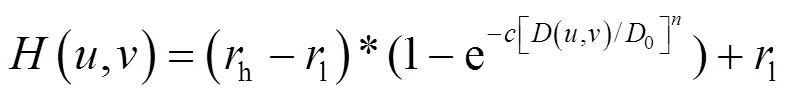
式中:C为锐化参数,设置c=1.2,高频增益rh=2,低频增益rl=0.5,D0=80,n=2。利用优化后的指数型同态滤波器对原始图像处理,得到处理后的图像如图7所示。
图7是经过优化的指数型高通滤波函数变化后处理的图像及其直方图。从图像直方图中可以看出,经过优化后的指数型同态滤波函数比原始指数型滤波函数具有更好分辨效果,对比更加明显:图6中灰度分量主要在0.4~0.8区间内,峰值在0.6左右;而图7中的灰度分量有明显的压缩,主要在区间0.4~0.6之间,峰值在大约0.5~0.6之间。说明图7相对于图6有更好的灰度对比效果。
3 总结
森林红外图像在经过本文设计的滤波器滤波后,图像的对比度和细节纹理得到了明显加强。在第2节中的滤波器选择中,确定了同态滤波器对森林红外图像有更好的处理效果。第3节中进一步优化了同态滤波器中的指数型滤波函数。本文所给出的滤波参数选择简单、效果明显,能满足大部分森林红外图像的加强,并能给类似红外图像提供有利的理论支持。文章所研究的算法能充分提高图像灰度层次感,改善图像的主观视觉质量,有利于后面进一步处理图像,具有一定的可靠性和实用性。
[1] Rafael C. Gonzalez, Richard E.Woods, Steven L.Eddins.[M]. Beijing: Publishing House of Electronics Industry, 2005: 120-123.
[2] 胡窦明, 赵海生, 李云川, 等. 一种基于同态滤波的红外图像增强新方法[J]. 红外技术, 2012, 34(4): 224-228.
[3] 王波. 滤波算法在图像增强中的应用研究[J]. 计算机仿真, 2013, 30(3): 364-407.
[4] Land E H . Recent advances in retinex theory and some implications for cortical computations: color vision and the natural image[J]., 1983, 80(16): 5163-5169.
[5] 刘斌, 金伟其, 王玲雪, 等. 基于空域和频域处理的红外图像细节增强算法[J]. 红外技术, 2011,33(8): 477-482.
[6] 李宏, 向遥, 张卫, 等. 基于直方图映射和分层的图像迁移算法研究[J]. 小型微型计算机系统, 2007, 28(6): 1110-1114.
[7] 简耀波. 红外图像处理中的关键算法研究[D]. 湖北: 华中科技大学, 2009: 1-16.
[8] 蒋立辉, 李宁, 成向阳, 等. 基于一种新的同态滤波算法的散斑噪声压缩[J]. 激光与红外, 2000, 30(1): 11-14
[9] 王冬梅, 路敬袆, 王秀芳. 基于Matlab的同态滤波算法的研究[J]. 科学技术与工程, 2010, 10(26): 62-65.
[10] Agaian S S, Panetta K A, Grigoryan A. Transform- based image enhancement algorithms with performance measure[J]., 2001, 10(3): 367-382.
[11] 夏清, 胡振琪, 位蓓蕾, 等. 一种新的红外热像仪图像边缘检测方法[J]. 红外与激光工程, 2014, 43(1): 319-322.
[12] Diallo M S, Schmitt D R . Noise reduction in interferometric fringe patterns with mean curvature diffusion[J]., 2004, 13(4): 819-831.
[13] 孙海江, 王延杰, 刘伟宁. 基于自适应平台阈值和拉普拉斯变换的红外图像增强[J]. 中国光学, 2011, 4(5): 474-479.
Algorithm of Infrared Image Enhancement for Forest Based on Fourier Transform
CUI Shuai,LIU Bo,DING De-hong
(410128,)
With the background of infrared monitoring technology applied in forest fire in forest, as the image characteristics of low contrast and great noise, the method of using Fourier transform is proposed to strengthen the picture in frequency domain.The forest infrared thermal image is enhanced by the ideal low-pass filter, Butterworth high-pass filter and homomorphic filter, respectively. with. According to the comparison, homomorphic filter overcomes the defects of the low pass and high pass filter and enhances details and contrast of image. An enhanced index homomorphic filtering function has been explored. Both the theory analysis and the experimental results show that the method can improve the definition of image and make more satisfactory image.
image enhancement,Fourier transform,infrared image,filter
TP391.41
A
1001-8891(2015)01-0029-05
2014-08-21;
2014-12-30.
崔帅(1988-),男,硕士研究生,研究方向:图像处理。
