网络直销型制造商开辟新渠道模式选择分析

曾 伟

（1.合肥工业大学 数学学院，安徽 合肥 230009；2.合肥工业大学 管理学院，安徽 合肥 230009）

网购这一新的消费模式的崛起，为新品牌的推广提供了良好的契机。由于网络销售可以节省大量的渠道流通费用和广告费用，在价格上有一定的优势。一些新品牌选择避开传统的零售市场，而直接通过网络渠道进行销售。大家熟知的戴尔、麦包包、芳草集、奥朵灯饰等网络热销品牌都是用这一营销战略成功打入市场并占有一席之地的。随着这些网络热销品牌有一定知名度后，也开始在传统零售终端销售。在此形势下，研究商家如何选择销售渠道模式，以及利用网络直销渠道和零售渠道销售是否合理，具有一定的现实意义。

近年来双渠道供应链竞争定价决策的研究得到了学者的广泛关注，文献［1］首先研究了确定需求下双渠道的定价问题，分析了直销渠道对传统零售渠道的定价、销售量与利润的影响；文献［2］研究了制造商利用直销渠道作为辅助渠道只销售剩余商品的问题；文献［3］研究了消费者需求依赖于价格和销售努力条件下的渠道选择问题，给出了增加直销渠道后，使制造商和零售商的收益均得到改善的条件；文献［4］研究了制造商是否应该在传统零售渠道的基础上增加网络直销渠道的决策；文献［5］分别讨论了双渠道中以制造商主导的Stackelberg定价策略和Bertrand定价策略，提出了不同条件下的最优定价策略；文献［6］研究了双渠道供应链的定价问题，讨论了制造商与零售商的决策互动对直销渠道的影响；文献［7］研究了考虑服务和价格时的双渠道供应链最优定价问题；文献［8］研究了集中型和分散型双渠道供应链中当生产成本中断发生时的定价和生产问题；文献［9］从博弈论的角度研究了双渠道供应链在不同联盟模式下各方的利润变化情况，探讨了实现整体联盟模式合作稳定的利润分配机制。以上文献为双渠道定价问题提供了可借鉴的方法，不过都是围绕传统零售商是否开辟网络直销渠道这一问题展开的，而针对目前出现的网络直销型制造商的渠道模式选择问题少有研究。其次，在博弈策略上，主要是以研究制造商Stackelberg为主，对零售商占主导地位的情况研究较少。

因此，本文讨论的问题如下：① 从网络直销型制造商的角度，考虑开辟零售渠道的条件；②分别研究制造商Stackelberg、零售商Stackelberg和双方Nash均衡3种不同权力结构下的双渠道选择问题；③认为市场份额是可控的参数，它一般受品牌效应、广告效应以及制造商产量主观分配等因素的影响，因此它可以被视为衡量制造商对渠道投入力度的重要参数。制造商可以通过改变对渠道的投入力度对渠道模式做出选择，在实践中有很强的操作性。

1 模型与记号

1.1 渠道模式

本文站在制造商的角度就渠道模式选择做出决策。假设制造商已经拥有一条网络直销渠道，记为I渠道。考虑到不同的决策模式和博弈顺序，制造商可以有以下4种渠道模式供选择：①I模式，即制造商只通过现有网络直销渠道销售；②IN博弈模式，即制造商增加零售渠道销售，但制造商与零售商各自决策；③IS博弈模式，即制造商增加零售渠道销售，制造商占主导地位，零售商是制造商的跟随者；④RS博弈模式，即制造商增加零售渠道销售，零售商占主导地位，制造商是零售商的跟随者。这4种模式在现实生活中都能找到其原型。I模式是指只通过网络直销渠道将商品销售给顾客的制造商，如Dell公司最初的营销战略正是这种模式的代表。IN模式、IS模式以及RS模式都是指制造商同时拥有网络直销渠道和零售渠道的双渠道进行销售。但不同的是：IN模式中，制造商和零售商实力相当，制造商将商品批发给零售商，各自为阵，互不干涉；IS模式中，制造商比零售商实力强，有话语权，比如选择代理商这类模式；而RS模式中，制造商实力不如零售商，需要通过零售商的品牌效应销售自己的产品。比如制造商寻找沃尔玛、家乐福、苏宁等这一类知名零售终端合作，需要缴纳一定的入场费等。

1.2 需求函数

考虑常见的确定线性需求函数，单渠道时记为：d0＝a－p0。双渠道时，渠道1为网络直销渠道，记d1＝（1－t）a－p1＋r1p2；渠道2为零售渠道，记d2＝ta－p2＋r2p1，其中d0、a、p0、di、pi、ri均大于0，0＜t＜1。a表示不考虑价格因素时的潜在市场规模；1－t表示网络渠道所占的初始市场份额，则t表示零售渠道所占的初始市场份额。市场份额t是可控的参数，它一般受品牌效应、广告效应以及制造商产量主观分配等因素的影响，因此t可以被视为衡量制造商对渠道投入力度的重要参数；pi表示零售价格；ri表示需求对其对手价格的敏感系数，由于需求主要受自身价格影响，所以ri＜1。根据常理，产品所占初始市场份额越大，需求抗价格干扰能力越强。在对自身价格敏感系数不变的情况下，对对手的价格敏感系数就越小，因此r1为（1－t）的反函数，r2为t的反函数，设r1＝1－（1－t），r2＝1－t。

1.3 符号说明

设c为商品成本；w2为零售渠道的批发价；g2为零售商单位产品赚取的利润；p2＞w2＞c＞0，g2＞0，则p2＝w2＋g2；ds为2条链的总需求，ds＝d1＋d2；π0为单渠道时的利润；π1为双渠道时网络直销渠道的利润；π2为零售渠道的利润；π2M、π2R分别为零售渠道制造商和零售商的利润，则π2＝π2M＋π2R；πM为制造商的总利润之和，包含网络直销渠道的利润和零售渠道中制造商的利润，πM＝π1＋π2M；πs为双渠道2条链的利润之和，πs＝π1＋π2；当渠道模式出现在上标时，表示该模式下对应的项，如πsIN表示IN模式下双渠道2条链的利润之和。

2 不同权力结构下的最优定价决策

2.1 I模式下最优定价决策

在I模式下，制造商以自身利润最大为目标来决定售价p0，其利润函数为：π0＝（p0－c）d0，由于d2π0/dp20＜0，则π0是p0的凹函数，由一阶最优条件可求得最优解：

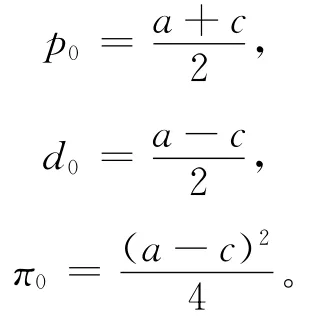
2.2 IN模式下最优定价决策

在IN模式下，制造商通过原有网络直销渠道和新增零售渠道销售产品，制造商与零售商各自决策。制造商的利润来源于网络直销渠道和批发商品给零售商所得，其决定网络直销渠道售价p1和零售渠道批发价w2，利润函数为：πM（p1，w2）＝π1＋π2M＝（p1－c）d1＋（w2－c）d2。零售商则决定零售渠道售价p2，但无论w2是多少，p2一定要高于w2，零售商才有利可图，所以零售商实际上决定的是g2，利润函数为：π2R（g2）＝g2d2。又由于d2π2R/＜0，πM的海森矩阵负定，则π2R和πM都是凹函数，由一阶最优条件联立3个方程可求得最优定价决策为：

2.3 IS模式下最优定价决策

在IS模式下，制造商通过原有网络直销渠道和新增零售渠道销售产品。制造商占主导地位，零售商是制造商的跟随者。该博弈过程运用逆向归纳法和子博弈纳什均衡原理求解，决策分为2个阶段：

（1）制造商给出网络直销渠道售价p1和零售渠道批发价w2后，零售商以自身利润最大化为目标来确定零售渠道售价p2，其利润函数为：π2R（p2）＝（p2－w2）d2。易证π2R是p2的凹函数，由一阶最优条件可得零售商的最优决策为：

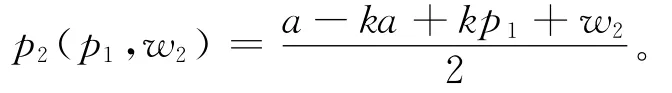
（2）制造商观察到该反应函数后，以自身利润最大化为目标，确定最优的p1和w2，其利润函数为：

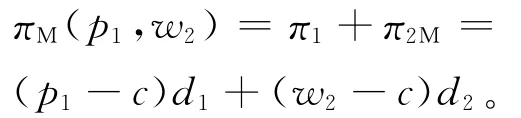
由于πM的海森矩阵负定，则πM是p1和w2的凹函数，由一阶最优条件联立2个方程可求得最优定价决策为：

则零售商的最优定价决策为：

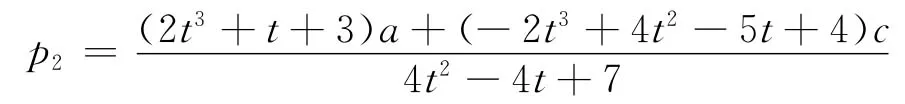
2.4 RS模式下最优定价决策

在RS模式下，制造商通过原有网络直销渠道和新增零售渠道销售产品。零售商占主导地位，制造商是零售商的跟随者。该博弈过程运用逆向归纳法和子博弈纳什均衡原理求解，决策分为2个阶段：

（1）零售商给出零售渠道批发所得纯利润g2后，制造商以自身利润最大化为目标来确定零售渠道批发价w2和网络直销渠道售价p1，其利润函数为：

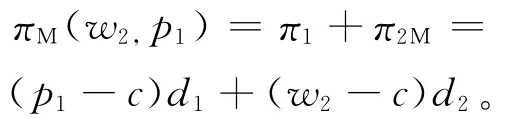
由于πM的海森矩阵负定，则πM是p1和w2的凹函数，由一阶最优条件联立2个方程可求得最优决策为：

（2）零售商观察到该反应函数后，以自身利润最大化为目标，确定最优的g2，其利润函数为π2R（g2）＝g2d2。又由于d2π2R/＜0，则π2R是g2的凹函数，由一阶最优条件可求得最优定价决策为：g2＝（a－c）/4。则

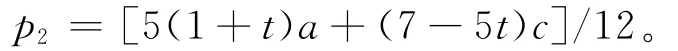
则制造商的最优定价决策为：

将上述3种不同权力结构下的最优定价决策代入各函数，得到各模型最优利润见表1所列。

表1 不同权力结构下的最优利润

3 渠道模式选择分析

作为网络直销渠道拥有者的制造商来说，首先要考虑2个主要问题：①是否需要开辟新的零售渠道；②如果要开辟零售渠道，哪一种模式下自己获利更多。

命题1（1）当t∈（0.159 4，0.840 6）时，π0＞；当t∈（0，0.159 4）∪（0.840 6，1）时，π0＜。

（2）当t∈（0.134 8，0.865 2）时，π0＞；当t∈（0，0.134 8）∪（0.865 2，1）时，π0＜。

（3）当t∈（0.084 0，0.916 0）时，π0＞；当t∈（0，0.084 0）∪（0.916 0，1）时，π0＜。

由该命题可以看出，当t接近于0或者1的时候，无论采用哪种模式，开辟零售渠道对制造商都是有利的。由于t表示零售渠道所占的初始市场份额，受品牌效应、广告效应以及制造商产量主观分配等因素的影响，反映出制造商对零售渠道所投入的力度。

当t接近于0时，表示已拥有网络直销渠道的制造商刚刚开辟零售渠道，销售主要依赖于网络直销渠道，此时开辟零售渠道作为补充可以增加制造商的收入。

当t从小变大时，就意味着制造商逐渐加大了对零售渠道的投入，越来越多的消费者购买商品从网络直销渠道转向零售渠道，此时2条渠道间的竞争加剧，内耗使部分利润流失，因此双渠道模式并未给制造商带来利润的增加。

而当t接近于1时，意味着制造商的营销策略彻底改变，商品的销售主要依靠于零售终端，此时单网络直销渠道给制造商带来的利润低于双渠道给制造商带来的利润，网络直销渠道只是作为零售渠道的补充，并且利用适当的竞争来提升零售渠道制造商获得的利润。

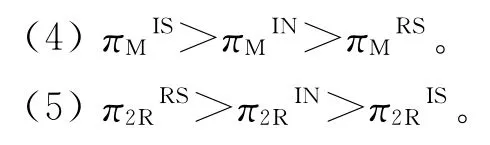
制造商在零售渠道的模式选择上，优先顺序为IS模式、IN模式、RS模式，因为制造商处于领导地位对自身一般是有利的。同理，零售商所得到的利润也按RS模式、IN模式和IS模式递减。

命题2（1）当t∈（0.350 7，0.649 3）时，π0＞；当t∈（0，0.350 7）∪（0.649 3，1）时，π0＜；

（2）当t∈（0.276 4，0.723 6）时，π0＞；当t∈（0，0.276 4）∪（0.723 6，1）时，π0＜。

（3）当t∈（0.268 1，0.731 9）时，π0＞；当t∈（0，0.268 1）∪（0.731 9，1）时，π0＜。

（4）＞≥，当t＝0.5时等号成立。

命题2从整体利润的角度比较了各模式下的利润大小，可以看出，当t∈（0.350 7，0.649 3）时，采用单网络直销渠道比采用双渠道获得的整体利润大，当t∈（0，0.350 7）或t∈（0.649 3，1）时，采用双渠道销售获利更多，而且此时最佳双渠道模式为IN模式。这说明当制造商刚刚开辟零售渠道时，若采用IN模式的双渠道，将获得最大的整体利益。随着制造商对零售渠道投入的进一步增大，达到三成多时，此时制造商对2条供应渠道的投入力度比较均衡或接近，由于竞争激烈，使整体利润部分流失，因此此时更适合单网络直销渠道销售。

如果制造商仍然继续加大对零售渠道的投入，接近七成时，若采用IN模式的双渠道，仍将获得最大的整体利益。这就意味着当对2条供应渠道的投入力度相差较大时，三七开以上力度，投入力度少的一方对多的一方不构成竞争威胁，此时两者并存并不会形成内耗而使整体利润流失，反而适当的竞争刺激了整体利润的提升。

命题3（1）≥＞，当t＝0.5时等号成立。

（2）＞≥，当t＝0.5时等号成立。

命题3比较了3种模式下网络直销渠道和零售渠道的利润大小，可以看出IS模式对网络直销渠道有利，而IN模式对零售渠道有利。这说明在IS模式中，虽然零售渠道中是制造商作为领导者，但零售渠道只是为网络直销渠道服务的，制造商的主要目标仍是网络直销渠道。

值得注意的是，对零售渠道最有利的模式并不是RS模式，而是IN模式。这或许是因为RS模式下虽然是零售商主导，但制造商在“后动”情况下，仍然是以网络直销渠道为主，所以其由批发所带来的利润对零售渠道贡献并不大。而在IN模式下，由于制造商并不知道零售商的决策，所以将投入更多的力量在零售渠道，所以对零售渠道的利润有所贡献。

结合命题2中的整体利润还可以看出，之所以IN模式的整体利润最高，主要得益于IN模式下零售渠道的利润贡献，也就是制造商在信息博弈不完全的情况下，加大了对零售渠道的投入。

在命题2和命题3中，均有当t＝0.5时，IS模式和RS模式的各渠道利润以及整体利润相等的情况。这说明当对2条渠道投入力度完全均衡时，无论由谁主导，零售渠道内部博弈不影响渠道间的利润分配，也就不影响整体利润。

通过以上命题及分析，可以得到如下管理启示：

（1）拥有单网络直销渠道的制造商仅从自身角度出发，可以开辟零售渠道，但零售渠道只能作为网络直销渠道的补充（控制在15%以下），在销售策略上应以网络直销渠道为主，控制对零售渠道的投入。或者彻底改变营销战略，只保留很少一部分网络直销渠道（控制在15%以下），对零售渠道进行大量投入，让网络直销渠道作为零售渠道的补充。在零售渠道模式上应选择IS模式进行销售。如果制造商对2种渠道的投入力度相当，2条渠道间的竞争加剧，那么内耗将使部分利润流失，双渠道模式并不能给制造商带来利润的增加。

（2）如果制造商能从供应链整体角度考虑的话，除了坚持两条渠道“一主一辅”的原则外，在零售渠道模式上应选择IN模式。当整体利润提升了，制造商和零售商在保证原有既得利益不变的情况下再对多余利润进行分配。至于具体怎么分割，可以通过双方谈判协商。这也为制造商提出有效的协调方案留下了空间。

（3）t表示零售渠道所占的初始市场份额，受品牌效应、广告效应以及制造商产量主观分配等因素的影响，它反映出制造商对零售渠道所投入的力度。制造商可以通过改变对渠道的投入力度实现对渠道模式的改变，在实际中可操作性强。

4 灵敏度分析

从以上的分析中可以看出，t是很重要的参数，它表示制造商对零售渠道的投入力度，1－t则表示制造商对网络直销渠道的投入力度。

命题4 ①、、为t的先减后增的凸函数；②、、为t的先减后增的凸函数；③、、为t的单调递增的凸函数；④、、为t的先减后增的凸函数；⑤、、为t的先减后增的凸函数。

根据命题4，利用一元函数的单调性和凹凸性t对各方利润影响如图1所示。图1所示一方面验证了各项利润的大小关系，另一方面直观地给出了t的变化对各项利润的影响。单渠道利润π0与t无关，所以呈水平线。

可以看出，各模式下的πs、πM、π2R均出现了先降后升的特点，图形关于t＝0.5对称，利润最值都出现在靠近2个端点处。π1也先降后升，但显然t越小对π1越有利，因为t越小，意味着对网络直销渠道的投入越大。而π2则表现为单调上升，并且上升幅度随t的增大而加快。在π1和π2的共同作用下，整体利润πs保持了先降后升的特点。

从图1可以看出，无论是制造商、零售商还是整体供应链，要想获得较高的利润，都要坚持“一主一辅”的原则，才能避免渠道间竞争引起的利润流失。

通过以上对t的灵敏度分析，找到了t的变化对各利润的影响及变化规律。从制造商的角度来看，可以通过改变对各个渠道的投入力度，从而改变各个渠道市场占有率。当不同渠道的市场占有率发生变化时，制造商能够及时掌握对应决策的变化规律，从而做出有利的决策。

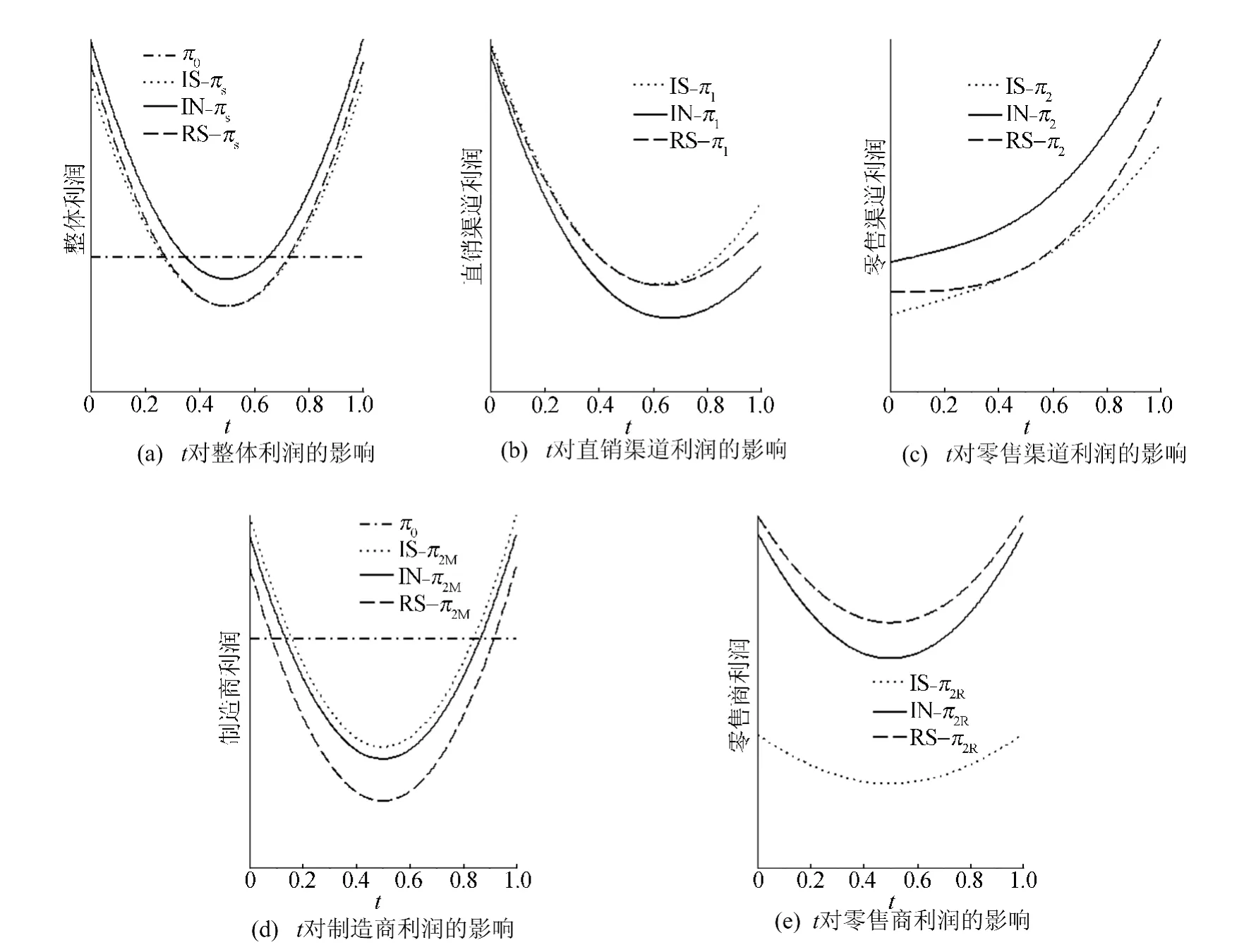
图1 t对各方利润的影响

5 结论

本文站在直销型制造商的角度研究了开辟新渠道模式选择的问题，分析总结出以下几点启示：① 当制造商已经拥有网络直销渠道销售产品时，可以开辟零售渠道来销售产品，但应以其中一种销售渠道为主，另一种销售渠道为辅，作为有益的补充，而选择双渠道模式应优先选择IS模式；② 制造商可以利用品牌效应、广告效应、促销活动以及产量主观分配等手段来调整对渠道的投入力度，从而调整产品的市场份额，从而满足当前渠道模式需要；③ 从供应链整体角度考虑，除了坚持2条渠道“一主一辅”的原则外，在零售渠道模式上应选择IN模式，这为制造商提出有效的协调方案提供了可能。

［1］Chiang W，Chhajed D，Hess J.Direct marketing，indirect profits：a strategic analysis of dual－channel supply－chain design［J］.Management Science，2003，49（1）：1－20.

［2］Tsan M C，Duan L，Houmin Y.Optimal returns policy for supply chain with e－market place［J］.International Journal of Production Economics，2004，88（2）：205－227.

［3］Agrawal T A N.Channel conflict and coordination in the ecommerce age［J］.Production and Operations Management，2004，13（1）：93－110.

［4］Kumar N，Ruan R.On manufacturer＇s complementing the traditional retail channel with a direct online channel［J］.Quantitative Marketing and Economics，2006，4（3）：289－323.

［5］郭亚军，曲道钢，赵礼强.基于电子市场的混合分销渠道定价策略研究［J］.系统工程学报，2008，23（5）：570－576.

［6］许传永，苟清龙，周垂日，等.两层双渠道供应链的定价问题［J］.系统工程理论与实践，2010，30（10）：1741－1752.

［7］Dan Bin，Xu Guangye，Liu Can.Pricing policies in a dualchannel supply chain with retail services［J］.International Journal of Production Economics，2012，139（1）：312－320.

［8］Huang Song，Yang Chao，Liu Hui.Pricing and production decisions in a dual－channel supply chain when production costs are disrupted［J］.Economic Modelling，2013，30（1）：521－538.

［9］浦徐进，诸葛瑞杰，曹文彬.不同博弈框架下的双渠道供应链联盟模式选择［J］.合肥工业大学学报：自然科学版，2014，37（8）：1002－1007.